作者简介: 胡桢麟, 1995年生,中国科学院上海光学精密机械研究所博士后 e-mail: huzhenlin@siom.ac.cn;王天泽, 1993年生,中国科学院上海光学精密机械研究所博士研究生 e-mail: tzwang@siom.ac.cn;胡桢麟,王天泽:并列第一作者
由于具有发光体积小、 能量转换效率高、 稳定性高和非相干等特点, 激光等离子体极紫外(LPP-EUV)光源在先进半导体制造与量测、 材料表面分析和EUV计量学等领域应用广泛。 本文开展了1 μm固体激光Sn等离子体EUV光源发射光谱诊断研究。 首先, 在真空中测量了不同激光峰值功率密度下1 μm激光激发固体Sn靶等离子体的13.5 nm带内辐射能量、 7~24 nm EUV波段和350~750 nm 可见光(VIS)波段的发射光谱, 计算了能量转换效率(CE)和光谱纯度(SP), 分析了激光峰值功率密度对Sn等离子体EUV光谱、 VIS光谱、 CE和SP的影响规律。 在本实验的参数范围内, CE随着激光峰值功率密度的提升先快速增大后缓慢减小, 在激光峰值功率密度为5.2×1011 W·cm-2时达到最大值2.47%。 SP随激光峰值功率密度的提升而增大, 在1.5×1012 W·cm-2时达到最大值7.52%。 然后, 基于Sn等离子体VIS波段的时间分辨光谱, 采用萨哈-玻尔兹曼图法和斯塔克展宽法计算了等离子体起爆后60~160 ns的电子温度( Te)和电子密度( ne), 研究了真空中Sn等离子体 Te和 ne随时间的演化规律, 并进一步分析了 Te和 ne对EUV波段辐射和13.5 nm带内辐射的影响规律。 结果表明, 激光峰值功率密度的上升会导致等离子体 Te和 ne的上升, Te和 ne的变化影响着不同电荷态离子的分布, 进而导致EUV辐射谱分布的变化。 在本实验的参数范围内, 随着 Te和 ne增大, CE先增大后减小, 而SP一直增大。 过低的 Te会导致Sn等离子体UTA峰位未达到13.5 nm, 过高的 Te会导致更多的驱动激光能量转化为13.5 nm以下的EUV辐射, 造成CE未达到最优。 以上研究结果为固体激光驱动LPP-EUV光源的工程化研发, 以及我国自主开展EUV光刻、 EUV计量与检测提供了研究基础与技术支持。
HU Zhen-lin and WANG Tian-ze: joint first authors
Due to their characteristics of a small luminous volume, high energy conversion efficiency, high stability, and coherence, laser-produced plasma extreme ultraviolet (LPP-EUV) light sources are widely used in the fields of advanced semiconductor manufacturing and inspection, material surface analysis, and EUV metrology. In this work, the emission spectrum diagnosis of a one μm solid-state laser Sn plasma EUV light source was carried out. First, the 13.5 nm in-band radiation energy, the emission spectrum of the 7~24 nm EUV band, and the 350~750 nm visible light (VIS) band of 1 μm laser-excited solid Sn target plasma in vacuum under different laser peak power densities were measured. The energy conversion efficiency (CE) and spectral purity (SP) were calculated, and the influence of laser peak power density on EUV and VIS spectrum, CE, and SP of Sn plasma was analyzed. Within the parameter range of this experiment, CE increases rapidly at first and then decreases slowly with the increase in laser peak power density, reaching a maximum value of 2.47% at a laser peak power density of 5.2×1011 W·cm-2. SP increases with the increase of laser peak power density and reaches a maximum value of 7.52% at 1.5×1012 W·cm-2. Then, based on the time-resolved VIS spectrum of Sn plasma, the electron temperature ( Te) and electron density ( ne) from 60 to 160 ns after plasma initiation were calculated using the Saha-Boltzmann plot and Stark broadening method, and the temporal evolution of Te and ne of Sn plasma in vacuum was studied. The influence of Te and ne on EUV band radiation and 13.5 nm in-band radiation was further analyzed. The results show that an increase in laser peak power density leads to an increase in plasma Te and ne, and the changes in Te and ne affect the distribution of ions with different charge states, causing a change in the EUV radiation spectral distribution. Within the parameter range of this experiment, CE initially increases and then decreases with the increase of Te and ne, whereas SP continues to increase. A Te value that is too low will prevent the UTA peak of Sn plasma from reaching 13.5 nm, and a Te value that is too high will cause more driving laser energy to be converted into EUV radiation below 13.5 nm, resulting in CE not reaching its optimal value. The above research results provide a research foundation and technical support for the engineering development of solid-state laser-driven LPP-EUV light source, as well as the independent development of EUV lithography, EUV metrology, and inspection in China.
激光等离子体极紫外(laser-produced plasma extreme ultraviolet, LPP-EUV)光源由于具有发光体积小、 能量转换效率高、 稳定性高和非相干等特点, 在先进半导体制造与量测、 材料表面分析和EUV计量学等领域发挥着重要作用[1, 2, 3, 4, 5]。 其中, 最有代表性的应用案例是荷兰ASML公司生产的EUV光刻机[6], 其搭载了激光锡(Sn)等离子体EUV光源, 可实现5 nm甚至更小技术节点的芯片制造, 已成为高端芯片大规模量产的必要设备。 商业化的LPP-EUV光刻光源采用CO2脉冲激光轰击高重频Sn液滴, 诱导产生等离子体, 收集镜将等离子体发射的中心波长为13.5 nm、 带宽为2%的EUV光收集并穿过中间焦点, 然后传输到光刻机的曝光系统中用于曝光硅晶圆。
驱动激光到13.5 nm(带宽2%)EUV辐射的能量转换效率(conversion efficiency, CE)是EUV光源工程化的重要指标[2], 商业化LPP-EUV光刻光源以波长为10 μm、 输出功率达万瓦级、 重复频率为50 kHz的窄脉冲CO2激光器作为驱动源, CE高达6%, 最终实现了大于250 W的EUV光输出[7, 8]。 相较于CO2激光, 波长为1 μm的固体脉冲激光器具有更好的光束质量、 更高的光电转换效率、 更优异的稳定性和更小的整机体积, 但其激发的Sn等离子体CE较低, 且还未能实现万瓦级功率高重频窄脉宽输出, 主要被用于驱动LPP-EUV量测光源。 瑞士苏黎世联邦理工学院(ETH Zurich)从2007年开始研发基于液滴Sn靶的LPP-EUV光源系统[9], 并于2021年成功在Adlyte公司实现量产, 该产品面向EUV掩膜版检测和晶圆量测, 采用输出功率1 300 W、 重频8~20 kHz的Nd:YAG脉冲激光器, CE为1.8%, 源功率达到23 W。 俄罗斯RnD-ISAN/EUV Labs公司研发的1 μm Nd:YAG激光驱动EUV量测光源采用液滴铟锡(Sn-In)合金靶[10, 11], 连续运行平均CE为2.5%, 最高CE为2.8%。 此外, 荷兰纳米光刻高级研究中心(ARCNL)也开展了基于液滴Sn靶的1 μm固体激光驱动EUV光源研究[12], 通过优化Sn液滴大小和激光峰值功率密度, 获得了高达3.2%的CE。 该研究还表明, 1 μm激光激发Sn等离子体CE的上限可能接近6%。 更高的CE可进一步提升固体激光驱动EUV光源的输出功率, 满足更高通量的量测需求, 甚至未来有望支持固体激光器成为新一代LPP-EUV光刻光源的驱动源。
激光等离子体的EUV辐射特性与其电子温度和密度密切相关[13, 14, 15]。 由于激光等离子体的临界密度与激光波长的平方呈反比(nc∝
基于此, 本文开展了1 μm固体激光Sn等离子体EUV光源发射光谱诊断研究。 首先, 采用不同激光峰值功率密度, 在真空中测量了1 μm激光激发固体Sn靶等离子体的13.5 nm带内辐射能量、 7~24 nm EUV波段和350~750 nm VIS波段的发射光谱。 计算了能量转换效率(CE)和光谱纯度(spectral purity, SP), 分析了激光峰值功率密度对Sn等离子体EUV光谱、 VIS光谱、 CE和SP的影响规律。 其次, 基于VIS波段的时间分辨发射光谱, 采用萨哈-玻尔兹曼图法和斯塔克展宽法计算了Te和ne, 研究了真空中Sn等离子体Te和ne随时间的演化规律。 最后, 研究分析了Sn等离子体Te和ne对EUV波段辐射和13.5 nm带内辐射的影响规律。
1 μm固体激光驱动等离子体EUV光源实验系统如图1所示。 实验采用输出波长为1 064 nm、 脉宽为4.8 ns、 最大输出能量为200 mJ的Nd:YAG调Q激光器作为激发Sn等离子体的驱动光源。 激光光束首先通过一个半波片(HWP)和偏振分束立方(PBS)实现能量调节, 然后经过45° 激光反射镜反射, 穿过一焦距为400 mm的平凸透镜后聚焦在高纯度固体Sn靶表面。 固体Sn靶固定在一个X-Y-Z-θ 四轴位移平台上, 使得每一发激光脉冲都能作用于平整的靶材表面。 在本实验中, 改变半波片的旋转角度可实现作用于Sn靶上的激光峰值功率密度的调节, Sn靶上激光聚焦光斑的半高全宽(FWHM)为40 μm。
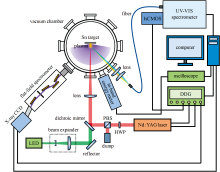 | 图1 1 μm固体激光驱动Sn等离子体极紫外光源实验系统原理图Fig.1 Schematic diagram of experimental platform for 1 μm solid-state laser-produced plasma EUV source |
采用实验室自研的平场光谱仪对激光激发Sn等离子体产生的EUV光谱进行测量, 光谱仪的采集角度与靶材表面法线呈50° 。 EUV光依次经过一对镀金Kirkpatrick-Baez(K-B)反射镜、 镀金平面反射镜和狭缝, 最后以87° 入射至栅距凹面光栅(中心刻线密度: 1 200 线· mm-1, 焦距: 235 mm)上, 所获得的衍射光成像到X射线CCD(英国Andor公司, DO940-BEN)上。 采用实验室自研的带内辐射能量计对Sn等离子体13.5 nm(带宽2%)的辐射能量进行测量, 能量计收光方向与与靶材表面法线呈26° 。 EUV光首先经过一对钼硅多层膜平面反射镜, 然后穿过一个直径为4 mm的光阑后入射至镀有锆膜的光电二极管上, 最后由示波器记录光电二极管产生的光电流。
采用光纤光谱仪(荷兰Avantes公司, AvaSpec-ULS4096CL-EVO)对Sn等离子体的紫外-可见光波段光谱进行了时间积分测量, 该光谱仪焦距为75 mm, 光栅刻线密度为300 线· mm-1, 狭缝大小为10 μm, 可实现350~750 nm波段光谱的一次性采集。 采用C-T成像光谱仪(北京卓立汉光仪器有限公司, Omni-λ 500i)和IsCMOS(卓立汉光, SIC-18U-VIS-4M-F)对Sn等离子体的可见光波段发射光谱进行了时间分辨测量, 该光谱仪焦距为500 mm, 光栅刻线密度为300 线· mm-1, 狭缝大小设置为10 μm, 可测量宽度为40 nm的光谱, 通过旋转光栅角度即可实现不同波段光谱的采集。 实验过程中, 光纤光谱仪和C-T成像光谱仪复用光谱收集光路, C-T成像光谱仪采集延迟时间为0 ns的时刻为激光等离子体的起爆时刻。
在实验过程中, 脉冲激光器的泵浦灯和Q开关工作于外触发模式, 两者的外触发信号均由数字脉冲延时发生器(美国SRS公司, DG645)提供, 真空腔室的真空度保持在10-5 Pa。 此外, 光路中还安装了一路绿色的LED指示光, 用于指示驱动激光辐照在靶材上的位置。 LED出光口放置一扩束镜, 用于调节LED指示光的焦点位置, 使LED指示光与驱动激光共焦。
在局部热力学平衡(LTE)假设下, 原子或离子谱线的峰值强度Iki可表示为[31]
式(1)中, Cs为粒子含量(数量分数), Aki为跃迁概率, gk为上能级简并度, Te为电子温度, Us(Te)为配分函数, Ek为上能级能量, KB为玻尔兹曼常数。 F为实验参数, 与光学系统效率、 等离子体体积与密度相关。
萨哈方程描述了电子密度Ne、 原子密度
式(2)中, UⅠ (Te)和UⅡ (Te)分别为原子和离子的配分函数, me为电子质量, h为普朗克常数, Eion为原子的第一电离能。
为了更精确地估计等离子体温度, 可联立式(1)和式(2)来绘制萨哈-玻尔兹曼(Saha-Boltzmann)图。 通过萨哈方程, 离子谱线强度
对式(1)和式(3)进行简单移项、 取对数处理后, 可整理得到
式(4)中,
其中, 上标Ⅰ 和Ⅱ 分别代表原子和一次离子。 需要注意的是, 由于y* 的计算式(6)中含有Te, 所以使用萨哈-玻尔兹曼图法时, 需给Te预设一个数值, 然后进行迭代计算, 让Te值收敛。
通过谱线的斯塔克展宽可计算等离子体的电子密度, 计算公式如式(8)[33]
式(8)中, Δ λ S为谱线的斯塔克展宽, ω s为电子碰撞系数,
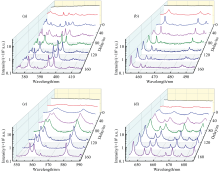
LPP光源的EUV波段辐射分布依赖于驱动激光的峰值功率密度。 图2展示了不同激光峰值功率密度下1 μm激光激发Sn等离子体的归一化EUV光谱, 各类高电荷态离子的主要发射波段已在图中标注, 13.5 nm(带宽2%)波段用半透明紫色块标出。 可以看出, Sn等离子体7~24 nm的EUV波段辐射呈现一个以13.5 nm附近为中心、 两边强度逐渐减弱的谱分布, 是Sn6+~Sn14+的4p64dN-4p54dN+1+4p64dN-14f(1≤ N≤ 6)密集跃迁产生的类连续跃迁阵列, 即不可分辨跃迁阵列(unresolved transition array, UTA)[34]。 其中, 13.5 nm附近的尖峰主要来自于Sn8+~Sn14+的发射, 13.5 nm即为EUV光刻机的工作波长。 17.3和19.3 nm处的尖峰分别来自于O5+和
 | 图2 平场光谱仪采集的7~24 nm波段的归一化极紫外光谱Fig.2 Normalized EUV spectra of 7~24 nm collected by the flat-field spectrometer |
转换效率(CE)和光谱纯度(SP)是LPP-EUV光源研究的两个重要参数[12]。 CE是驱动激光的输出能量和等离子体13.5 nm带内辐射能量之比, 足够高的CE是LPP-EUV光源工程化的关键。 SP是13.5 nm带内辐射能量与EUV波段的总辐射能量之比, SP数值越高意味着在EUV波段, 更多的辐射能量集中在13.5 nm(带宽2%)带内波段。 在本实验中, 我们定义13.5 nm(± 1%)带内辐射能量与7~20 nm的总辐射能量之比为SP。 在不同激光峰值功率密度下, 1 μm激光激发Sn等离子体的CE和SP如图3所示。 由图可见, 在本实验的参数范围内, CE随着激光峰值功率密度的提升先快速增大, 在激光峰值功率密度为5.2× 1011 W· cm-2时达到最大值2.47%, 然后缓慢减小; SP随激光峰值功率密度的提升而增大, 在1.5× 1012 W· cm-2时达到最大值7.52%。 已有研究表明, CE的上限是SP的二分之一[12]。 在本实验中, 当CE达到最大值2.47%时, SP为7.0%, 这意味着在理论上CE还有提升的空间。 此外, 当激光峰值功率密度大于5.2× 1011 W· cm-2时, SP增大同时CE减小意味着激光到EUV波段辐射的能量转换效率下降, 更多的激光能量转化为其他波段的辐射和高能粒子碎屑的动能, 该情况不利于LPP-EUV光源工作[36]。
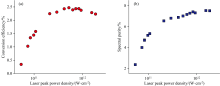 | 图3 Sn等离子体的(a)转换效率和(b)光谱纯度随激光峰值功率密度的变化趋势Fig.3 Dependence of (a) CE and (b) SP of Sn plasma on laser peak power density |
不同峰值功率密度1 μm激光激发Sn等离子体350~750 nm的时间积分发射光谱如图4所示。 光纤光谱仪设置的开始采集时间早于等离子体起爆时刻, 采集积分时间设置为1 ms, 完全覆盖等离子体的存在时间。 由图可见, Sn等离子体的可见光(VIS)波段发射光谱主要由连续背景和在连续背景之上的线状谱构成, VIS发射光谱的强度随着激光峰值功率密度的上升而增大。 其中, 连续背景主要由韧致辐射和电子-离子复合辐射构成, 线状谱线主要来自于Sn原子和Sn+~Sn3+的跃迁辐射。 在局部热力学平衡(LTE)假设下, 等离子体中的电子温度、 离子温度和电子激发温度均相等, 所以我们可以基于萨哈-玻尔兹曼图法采用Sn原子和离子的线状谱线强度来计算得到等离子体的电子温度。
 | 图4 光纤光谱仪采集的350~750 nm波段时间积分光谱Fig.4 Temporal integral spectra of 350~750 nm collected by the fiber-optic spectrometer |
根据光纤光谱仪的时间积分光谱测量结果, 我们进一步使用具有更高光谱分辨率的C-T成像光谱仪采集了Sn等离子体4个VIS波段的时间分辨发射光谱, 4个波段分别为372~415、 451~494、 547~590和642~685 nm, 所设置的光谱仪采集门宽为10 ns, 增益为50%, 光谱采集延迟时间为20、 40、 60、 80、 100、 120、 140和160 ns, 实验结果如图5所示。 可见, 在等离子体演化早期, VIS波段的发射光谱主要为连续谱, 这是由于早期等离子体电子密度非常高, 等离子体在该波段可以近似为黑体。 随着延时逐渐增大, 连续谱的强度逐渐减弱, 在等离子体起爆60 ns以后才出现较为清晰的线状谱线, 并且谱线的展宽逐渐减小, 这意味着电子密度的减小。 我们从这4个波段中可以挑选出2条Sn原子谱线和4条Sn+谱线, 用于绘制萨哈-玻尔兹曼图并计算等离子体的Te, 这6条谱线的具体参数如表1所示。 此外, 采用Sn Ⅱ 645.35 nm这条谱线的斯塔克展宽来计算等离子体的ne。
| 表1 用于绘制萨哈-玻尔兹曼图的Sn原子和离子谱线及其参数 Table 1 Atomic and ionic spectral lines of Sn and their parameters for Saha-Boltzmann plot construction |
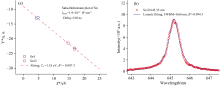
图6(a)和(b)分别展示了基于Sn谱线绘制的萨哈-玻尔兹曼图和Sn Ⅱ 645.35 nm谱线的洛伦兹函数拟合结果, 所对应的激光峰值功率密度为1.9× 1012 W· cm-2, 光谱采集延时为160 ns。 两者拟合结果的决定系数(R2)分别为0.997 3和0.994 5, 均具有较高的拟合精度。
已有研究表明, Sn等离子体发射EUV光的时间段与激光脉冲的持续时间重合[11], 本实验采用的激光脉宽为4.8 ns, 所以等离子体EUV辐射的持续时间约为10 ns。 然而VIS波段的发射光谱在40 ns延时内呈连续谱, 导致无法采用萨哈-玻尔兹曼图法和斯塔克展宽法计算Sn等离子体起爆到40 ns内的Te和ne。 Te和ne在等离子体起爆后60~160 ns内的变化趋势如图7(a)所示, 等离子体的Te和ne呈现减小趋势。 由于激光等离子体的演化具有连续性[21, 37, 38], 因此等离子体演化后期的Te和ne可在一定程度上反映等离子体演化早期的Te和ne。
 | 图7 Sn等离子体电子温度与密度随(a)光谱采集延时与(b)激光峰值功率密度的变化趋势Fig.7 Dependence of electron temperature and density of Sn plasma on (a) spectral acquisition delay and (b) laser peak power density |
为进一步研究Te和ne对Sn等离子体EUV辐射特性的影响规律, 采用VIS波段发射光谱计算了不同激光峰值功率密度下Sn等离子体的Te和ne。 Te和ne随激光峰值功率密度的变化趋势如图7(b)所示, 可见, 作用于Sn靶的激光峰值功率密度的上升会导致等离子体Te和ne的上升。 Te和ne的上升意味着等离子体平均电荷态的增大, 导致更高电荷态离子密度的上升, 且较低电荷态离子密度的下降。 图2所展示的归一化EUV光谱的变化趋势进一步说明, 当Te逐渐增大时, Sn8+~Sn14+密度逐渐上升, 同时Sn5+~Sn7+密度逐渐下降。 在本实验的参数范围内, 随着Te和ne增大, CE先增大后减小, 而SP一直增大。 对于EUV光刻或基于13.5 nm EUV光的EUV掩模检测, 需要LPP光源13.5 nm带内辐射的CE尽可能高, 过低的Te会导致Sn等离子体UTA峰位未达到13.5 nm, 过高的Te会导致更多的驱动激光能量转化为13.5 nm以下的EUV辐射, 造成CE未达到最优。 基于宽带EUV光的半导体量测希望LPP的EUV辐射分布更为平坦, 过高的Te会导致SP过大, 光谱平坦度下降。 此外, Sn等离子体UTA的峰值强度和等离子体ne均随激光峰值功率密度上升, 说明提高激光峰值功率密度会增加靶材烧蚀量和电离程度, 进而使高电荷态Sn离子数量增加, 最终导致更多的高电荷态Sn离子辐射EUV光[39]。
本文开展了1 μm固体激光Sn等离子体EUV光源发射光谱诊断研究。 首先, 探究了激光峰值功率密度对1 μm激光激发Sn等离子体EUV波段和VIS波段发射光谱的影响规律。 随着激光峰值功率密度的上升, Sn等离子体的EUV光谱峰值强度增大, 长波波段辐射在整个EUV波段的占比逐渐减小, 同时短波波段辐射占比逐渐增大。 且只有当激光峰值功率密度足够高时, Sn等离子体UTA峰的中心波长才能位于13.5 nm处。 计算了转换效率(CE)和光谱纯度(SP), 在本实验的参数范围内, CE随着激光峰值功率密度的提升先快速增大, 在激光峰值功率密度为5.2× 1011 W· cm-2时达到最大值2.47%, 然后缓慢减小; SP随激光峰值功率密度的提升而增大, 在1.5× 1012 W· cm-2时达到最大值7.52%。 基于Sn等离子体VIS波段时间分辨发射光谱, 采用萨哈-玻尔兹曼图法和斯塔克展宽法计算了Sn等离子体起爆后60~160 ns的电子温度(Te)和电子密度(ne)。 进一步研究表明, 激光峰值功率密度的上升会导致等离子体Te和ne的上升, Te和ne的变化影响着不同电荷态离子的分布, 进而导致EUV辐射谱分布的变化。 以上研究结果为固体激光驱动LPP-EUV光刻光源和量测光源的工程化研发提供了研究基础, 对我国自主开展EUV光刻、 EUV计量与检测具有重要意义。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|