椭偏技术是一种通过测量偏振光入射待测物前后偏振态的变化来获取其光学常数(折射率n, 消光系数k)、 膜厚及表面形貌等参数的一种高精度、 非接触和无损的光学测量技术之一^[1]。 紫外到近红外波段的光谱椭偏技术在半导体、 光伏、 显示、 材料等领域已被广泛应用。 随着技术的发展, 一些红外波段的光学薄膜也被应用, 如芯片制造过程中作为钝化、 涂层等^[2]; 军事目标的隐身涂料、 生物敏感层^[3]等。 为适应不同材料的薄膜测量需要, 需拓展光谱椭偏的光谱范围。 但受限于红外光源能量较弱和红外偏振器的性能不理想, 红外光谱椭偏测量技术的发展一直较为缓慢。 1975年, Stobie等^[4]研制出第一台中远红外波段(3 100~3 660 nm)椭偏仪, 该仪器采用单色仪进行光谱扫描和旋转起偏器进行偏光调制, 并研究了甲酸薄膜的红外光学性质。 但旋转器/检偏器型红外椭偏仪存在探测器的偏振敏感度问题, 且单色仪扫描灵敏度低和光谱扫描测量速度较慢^{[5, 6]}。 1993年, Rö seler等^[7]提出一种基于傅里叶变换的红外光谱椭偏仪, 通过一次测量即可获取整个红外波段的光谱, 极大地缩短了测量时间。 此后, 基于傅里叶变换的红外光谱椭偏仪得到迅速发展。 2018年, Furchner等^[8]提出一种用于表征结构表面形貌和薄膜的高通量红外光谱穆勒矩阵椭偏仪; 2019年, Liu等^[9]提出一种中红外(1 500~5 500 nm)穆勒矩阵椭偏测量系统, 并对空气和二氧化硅标准薄膜样品进行测量。 同年, 李清灵等^[10]采用北京量拓科技有限公司ESIU型光谱椭偏仪对油膜进行了紫外可见-近红外(270~900 nm)的光谱偏振特性分析。

目前, 同时实现紫外到中红外的宽波段光谱椭偏测量技术较少, 为此本文重点开展对光栅+傅里叶光谱的宽波段光谱椭偏测量的研究, 通过集成椭偏仪实现192~3 200 nm光谱范围内单层和多层薄膜膜厚的测量, 实验结果表明该椭偏仪不仅具有较高的测量精度, 而且具有较快的测量速度。

宽波段大角度光谱椭偏基本原理如图1所示, 主要由紫外到短波红外起偏臂PSG(UV-SWIR)、 短波红外到中波红外起偏臂PSG(SWIR-MIR)、 检偏臂PSA和样品台S四部分组成, 其中检偏臂PSA由紫外到短波红外PSA(UV-SWIR)和短波红外到中波红外PSA(SWIR-MIR)两个检偏臂单元组成。 根据透反射及入射角要求, 检偏臂PSA和样品台S可大角度旋转。

图1

Fig.1

	Figure Option ViewDownloadNew Window
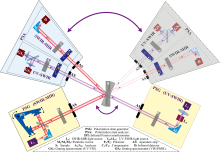	图1 基于光栅+傅里叶光谱的宽波段大角度光谱椭偏原理结构图Fig.1 Schematic diagram of wide-band, large-angle spectroscopic ellipsometry based on grating and Fourier spectroscopy

PSG(UV-SWIR)与PSA(UV-SWIR)组成紫外到短波红外(192~2 100 nm)光谱椭偏测量系统。 采用PSG复色光源加PSA光栅光谱的方式, 采用背透式氘灯L₂和钨灯L₃, 满足192~2 100 nm光谱范围要求; 通过石英透镜实现钨灯和氘灯的光路重合; 采用离轴抛物面反射镜M₂, 实现无色差的反射式光路准直; 采用自动光阑AS自动控制不同档位光阑, 实现测试能量的自动控制; 采用洛匈棱镜P₂, 实现宽光谱的起偏; 起偏后的光通过样品S后进入检偏臂PSA, 通过旋转消色差补偿器C₂对被测光进行偏振调制; 在检偏器A₂后光束直接进入紫外可见光谱仪GS₁(光谱范围192~1 000 nm)和近红外光谱仪GS₂(光谱范围1 000~2 100 nm)。

PSG(SWIR-MIR)与PSA(SWIR-MIR)组成短波红外到 中波红外(2 000~3 200 nm)光谱椭偏测量系统。 红外光源硅碳棒L₁发出的光通过镀金的离轴抛物面镜M₁准直, 经过傅里叶红外干涉具IFI进行干涉调制; 经过中红外起偏棱镜P₁从自动光阑AS口出射, 起偏后的光通过样品S后进入检偏臂PSA; 通过旋转消色差补偿器C₁对被测光进行偏振调制; 经过检偏器A₁后, 光束通过离轴抛物面镜M₂聚焦在近红外短波红外MCT光电探测器D。

以Stokes矢量描述偏振光束, 穆勒矩阵描述光学元件和样品的偏振特性, 出射光束的斯托克斯S_out表示为

Sout=MAMCMSMPSin(1)

式(1)中, S_in=[I, 0, 0, 0]^T, S_out=[I', Q', U', V']^T, M_P、 M_C、 M_S、 M_A分别为起偏器、 补偿器、 样品和检偏器的穆勒矩阵。 其中, M_P、 M_C、 M_S、 M_A分别表示为

$\begin{array}{l}\boldsymbol{M}_{\mathrm{P}}=\left[\begin{array}{cccc}1 & \cos (2 \alpha) & \sin (2 \alpha) & 0 \\\cos (2 \alpha) & \cos ^{2}(2 \alpha) & \cos (2 \alpha) \sin (2 \alpha) & 0 \\\sin (2 \alpha) & \cos (2 \alpha) \sin (2 \alpha) & \sin ^{2}(2 \alpha) & 0 \\0 & 0 & 0 & 0\end{array}\right] ; \\\boldsymbol{M}_{\mathrm{A}}=\left[\begin{array}{cccc}1 & \cos (2 \beta) & \sin (2 \beta) & 0 \\\cos (2 \beta) & \cos ^{2}(2 \beta) & \cos (2 \beta) \sin (2 \beta) & 0 \\\sin (2 \beta) & \cos (2 \beta) \sin (2 \beta) & \sin ^{2}(2 \beta) & 0 \\0 & 0 & 0 & 0\end{array}\right] ; \end{array}$ MC=10000cos2(2γ)+sin2(2γ)cos(δ)cos(2γ)sin(2γ)(1-cos(δ))-sin(2γ)sin(δ)0cos(2γ)sin(2γ)(1-cos(δ))sin2(2γ)+cos2(2γ)cos(δ)cos(2γ)sin(δ)0sin(2γ)sin(δ)-cos(2γ)sin(δ)cos(δ); MS=1-cos(2Ψ)00-cos(2Ψ)10000sin(2Ψ)cos(Δ)sin(2Ψ)sin(Δ)00-sin(2Ψ)sin(Δ)sin(2Ψ)cos(Δ)

其中, I为入射光的光强, I'为到达光电探测器D、 光谱仪GS₁和GS₂的光强。 由于探测器和光谱仪只能获得Stokes参量S_out中的I', 因此根据式(1), I'可表示

I'=IK(2)

式(2)中,

$ \begin{array}{l}K=\left[\frac{1}{2}(\cos 2 \alpha \cos 2 \beta-\cos 2 \Psi \cos 2 \beta+\sin 2 \Psi \cos \Delta \sin 2 \alpha \sin 2 \beta)(1\right. \\+\cos \delta)-\cos 2 \Psi \cos 2 \alpha+1-\sin 2 \Psi \sin \Delta \sin 2 \alpha \sin 2 \beta \sin \delta \cos 2 \gamma+ \\\sin 2 \Psi \sin \Delta \cos 2 \alpha \cos 2 \beta \sin \delta \sin 2 \gamma+\frac{1}{2}(\cos 2 \alpha \cos 2 \gamma-\cos 2 \Psi \cos 2 \beta \\-\sin 2 \Psi \cos \Delta \sin 2 \alpha \sin 2 \beta)(1-\cos \delta) \cos 4 \gamma+\frac{1}{2}(\cos 2 \alpha \sin 2 \beta- \\\cos 2 \Psi \sin 2 \beta+\sin 2 \Psi \cos \Delta \sin 2 \alpha \cos 2 \beta)(1-\cos \delta) \sin 4 \gamma]\end{array} $

其中α 和β 分别为起偏器和检偏器的偏振方向角, γ 为补偿器的光轴方位角(任意波片), δ 为补偿器的调制相位, Ψ 和Δ 为样品的被测椭偏参量的振幅比和相位差。

对于紫外到短波红外波段(UV-SWIR)来说, 起偏臂光源为复色光, 经过检偏臂后由光谱仪分光, 光谱仪GS₁和GS₂可获得不同波长λ 在不同旋转补偿器角度下的调制光强为

I'(λ)=I(λ)K(3)

对于短波红外到中波红外波段(SWIR-MIR)来说, 起偏臂光源为经过迈克尔逊干涉具后的调制信号, 经过检偏臂后去掉直流分量, 通过傅里叶逆变换获得分光光谱, 因此式(2)可表示为

I'(t)=K∫λ1λ2I(λ)1+cos2πktλdλ⇒I'(λ)=K∫0LI'(t)cos2πktλdt(4)

式(4)中, λ ₁为光谱范围内最小波长, λ ₂为光谱范围内最大波长, k是干涉光程差随时间的系数, L为傅里叶红外干涉具最大调制光程差。

根据上述理论, 通过采集补偿器在不同方位角所对应的调制光谱, 结合椭偏测量理论和线性回归算法, 即可求出样品膜厚、 折射率、 消光系数等参数。

搭建的宽波段大角度光谱椭偏测量原理样机如图2所示, 为了更快的准确对准, 样机中加入了十字对准装置, 紫外到近红外波段采用两个光栅光谱仪(光谱范围192~1 000 nm, Maya2000pro和Nirquest), 傅里叶红外干涉具IFI定制(光谱范围2 000~3 200 nm, Foli10-R, 荧飒光学科技有限公司)。 分别对空气(透射式)、 半导体、 电介质、 金属、 聚合物、 多层膜等多种薄膜进行测试, 验证其测量薄膜厚度和折射率的重复测量精度。 其中, 薄膜样片采用国防科技工业光学一级计量站标定后的不同厚度、 不同材料、 不同膜层数的多个样片。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 原理样机实物图Fig.2 Experimental device diagram

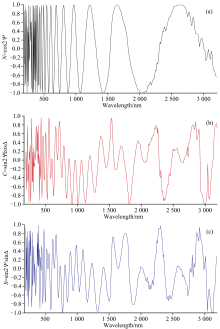
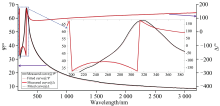
样机入射角设置70° , 根据式(1)— 式(4)和光谱椭偏理论^{[11, 12]}, 测得标定后SiO₂-Si标准样片(SiO₂厚度d=62.5 nm)的穆勒矩阵M_S中的N=cos2Ψ 、 C=sin2Ψ cosΔ 和S=sin2Ψ sinΔ 与波长的关系分别如图3(a)、 图3(b)和图3(c) 所示, 进而计算获得样片椭偏参数Ψ 和Δ 与波长的关系分别如图4的黑实线和红实线所示, 通过光谱椭偏构建SiO₂-Si光学模型, 根据测量椭偏参量算法回归获得椭偏参数Ψ 和Δ 如图4的红虚线和黑虚线所示, 进而反演得到样片薄膜的膜厚。

图3

Fig.3

Figure Option ViewDownloadNew Window

图3 样机测得样片穆勒矩阵元素N、 C、 S与波长的对应曲线(SiO2-Si样片, SiO2厚度d=62.5 nm)(a): 测得N=cos2Ψ 与波长的对应曲线; (b): 测得C=sin2Ψ cosΔ 与波长的对应曲线; (c): 测得S=sin2Ψ sinΔ 与波长的对应曲线Fig.3 The results of Muller matrix elements N, C, S versus wavelength measured by the prototype (SiO2-Si sample, SiO2 thickness d=62.5 nm) (a): The measured curve of N=cos2Ψ corresponds to the wavelength; (b): The measured curve of C=sin2Ψ cosΔ corresponds to the wavelength; (c): The measured curve of S=sin2Ψ sinΔ to the wavelength

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 样机测得样片椭偏参量(Ψ , Δ )与波长的对应曲线(SiO2-Si样片, SiO2厚度d=62.5 nm)Fig.4 The corresponding curve of the ellipsometry parameter (Ψ , Δ ) of the sample measured by the prototype and the wavelength (SiO2-Si sample, SiO2 thickness d=62.5 nm)

采用上述同样的方法, 样机对Si基底上不同薄膜材料、 不同厚度、 不同膜层样片进行测量, 其中SiO₂-Si(薄膜为电介质)、 ZnO-Si(薄膜为半导体)、 PI-Si(薄膜为聚合物)、 Si₃N₄-Al₂O₃-Si(电介质双层膜)、 Au-SiO₂-Si(金属电介质双层膜)各进行30次测量后的厚度测量精度及重复测量精度如表1所示, 由实验结果显示厚度测量精度优于0.7 nm, 厚度重复测量精度优于0.04 nm。

表1

Table 1

表1(Table 1)

表1 样机对不同类型薄膜样片测得的厚度及精度 Table 1 The thickness and accuracy of different types of film samples measured by the prototype 薄膜样品类型 薄膜材料 薄膜厚度 d/nm 样机测得薄膜 平均厚度 d̅/nm 厚度精度 Δ d/nm 厚度重复测量精度 δ d/nm SiO2-Si SiO2 62.5 62.7 0.2 0.03 SiO2-Si SiO2 1 084.6 1 084.1 0.5 0.04 ZnO-Si ZnO 152.3 152.7 0.4 0.02 PI-Si PI 402.4 402.1 0.3 0.03 Si3N4-Al2O3-Si Si3N4 114.9 114.3 0.6 0.04 Al2O3 26.0 26.7 0.7 0.03 Au-SiO2-Si Au 23.2 23.5 0.3 0.02 SiO2 104.8 104.7 0.1 0.02 注: d̅=∑i=130di30, Δd=d-d̅, δd=∑i=130(di-d̅)2n-1

表1 样机对不同类型薄膜样片测得的厚度及精度 Table 1 The thickness and accuracy of different types of film samples measured by the prototype

针对现有光谱椭偏光谱范围有限, 导致可测材料有限等问题, 提出一种基于光栅+傅里叶光谱的宽波段大角度光谱椭偏测量技术, 其中紫外-短波红外波段采用光栅光谱椭偏技术, 短波红外-中红外采用傅里叶光谱椭偏技术, 采用卧式旋转方式, 并进行原理样机集成, 最终实现192~3 200 nm宽波段光谱椭偏测量。 对Si基底上SiO₂-Si(薄膜为电介质)、 ZnO-Si(薄膜为半导体)、 PI-Si(薄膜为聚合物)、 Si₃N₄-Al₂O₃-Si(电介质双层膜)、 Au-SiO₂-Si(金属电介质双层膜)等不同薄膜材料、 不同厚度、 不同膜层样片进行测量, 实验结果表明, 薄膜厚度测量精度优于0.7 nm, 重复性测量精度可达0.04 nm(30次重复测量)。 该测量技术在高精度、 宽波段、 大角度薄膜椭偏测量领域有重要的应用前景, 并且可根据不同材料选择最优的光谱波段, 进而提高光谱椭偏测量材料的类型。