荧光分光光度计F-7000, 日本日立株式会社。 品牌花生和大豆油购于许昌市胖东来超市。

1.2.1 样品的制备

从市场上3个不同批次的大豆油和花生油, 勾兑成大豆油与花生油的伪品, 花生油含量0~100%(体积比), 步长为5%。 共计63个样本。

1.2.2 EEM数据采集

将自制的花生油伪品放入10 mm× 10 mm石英荧光比色皿中测量, 其光源为150 W氙灯, PMT电压为700 V。 激发波长范围为250~550 nm, 采样间隔为10 nm, 共包含31个激发波长。 发射波长范围为260~750 nm, 采样间隔为10 nm, 共包含50个发射波长。 扫描速度为12 000 nm· min^-1, 使用荧光光谱仪前预热30 min。

实验得到63个50× 31二维数据矩阵, 采用三角形内插值法去除拉曼散射和瑞利散射^[19]。 去除拉曼散射和瑞利散射后再对荧光光谱进行卷积平滑(Savitzky-Golar)处理。

将每条激发波长下的发射波长展开, 并按照激发波长顺序数将所有发射波长重构, 从而将原EEM的二阶数据转化成一阶荧光光谱数据向量。 采用WPD对每个激发波长对应的发射光谱进行分解^{[16, 17, 18, 19, 20]}, 计算小波系数。 WPD的基函数一般采用4 阶Symlet小波。 选择3层WPD对EEM光谱数据进行分解。

EEM数据去除瑞利散射后对光谱进行Savitzky-Golar卷积平滑处理, 采用ATLD算法和PARAFAC算法预测花生油伪品中的花生油含量。 ATLD和PARAFAC算法请参考文献[21, 22]。 对EEM光谱数据进行Savitzky-Golar卷积平滑处理后, 进行3层WPD, 选取最低频段小波系数作为输入值, 花生油含量为输出值进行PLS和BP-ANN模型构建。 BP-ANN采用3层的网络结构: 输入层为199、 隐含层为4、 输出层为1, 训练函数为Scaled conjugate Gradient。 PLS算法、 ATLD算法和PARAFAC算法从样本中随机选取70%的样本构造训练集(43个样本), 30%的为测试集(20个样本)。 ANN算法随机选取70%的样本构造训练集(43个样本), 15%为测试集(10个样本), 15%为验证集(10个样本)。

使用平均绝对偏差(mean absolute deviation MAD)[式(1)]、 均方误差(mean squared error, MSE)[式(2)]和均方根误差(root mean squared error, RMSE)[式(3)]来评价模型^[23]。

MAD=∑i=1n|At-Ft|n(1)

MSE=∑i=1n(At-Ft)2n(2)

RMSE=∑i=1n(At-Ft)2n(3)

式(1)— 式(3)中: A_t为实际花生油含量; F_t为预测花生油含量; n为试验中使用的样品数。

采用软件Origin 2021(OriginLab公司)进行箱线图+正态曲线图的制作; PLS, ANN, ATLD, PARAFAC模型通过软件Matlab R2020b(美国MathWorks公司)自编程序完成。

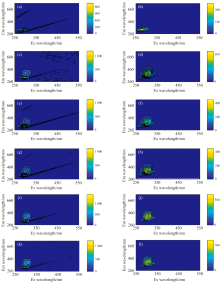
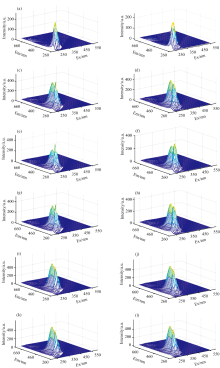
对大豆油、 花生油EEM光谱进行去散射处理前后情况如图1所示。 EEM光谱数据通过三角形内插值法消除瑞利散射和拉曼散射, 花生油和大豆油的EEM光谱存在差异。 结果表明, 纯花生油的EEM数据在(Ex=280 nm, Em=320 nm)附近有一个荧光强度较高的扇贝状峰, 纯大豆油的EEM数据在(Ex=300 nm, Em=410 nm)附近存在一个荧光强度较高的扇贝状峰, 但是花生油和大豆油荧光吸收峰的波长范围及荧光强度存在一定差异, 这可能是由于花生油含维生素E, 特别是α -生育酚, 而大豆油则以γ -生育酚为主, 其γ -生育酚EEM光谱特性与α -生育酚EEM光谱有差异, 另外可能是由于大豆油和花生油的加工条件差异所引起的, 维生素及其衍生物生育酚、 生育三烯酚所产生的EEM光谱主要在这个区域。 此外, 纯大豆油的EEM光谱在(Ex=330 nm, Em=400 nm)附近还有一个荧光强度较弱的峰, 这为大豆油掺假花生油提供了定量分析基础。 图2为EEM光谱平滑前后的对比图, 等高线边缘平整有利于后续进行花生油的含量预测。

图1

Fig.1

Figure Option ViewDownloadNew Window

图1 大豆油和花生油去散射前后荧光光谱对比图 (a): 花生油荧光光谱去散射前; (b): 花生油荧光光谱去散射后; (c): 80%花生油荧光光谱去散射前; (d): 80%花生油荧光光谱去散射后; (e): 60%花生油荧光光谱去散射前; (f): 60%花生油荧光光谱去散射后; (g): 40%花生油荧光光谱去散射前; (h): 40%花生油荧光光谱去散射后; (i): 20%花生油荧光光谱去散射前; (j): 20%花生油荧光光谱去散射后; (k): 大豆油荧光光谱去散射前; (l): 大豆油荧光光谱去散射后Fig.1 Fluorescence spectra of soybean oil and peanut oil from before and after de-scattering (a): Peanut oil fluorescence spectrum before de-scattering; (b): Peanut oil fluorescence spectrum after de-scattering; (c): 80% peanut oil fluorescence spectrum before de-scattering; (d): 80% peanut oil fluorescence spectrum after de-scattering; (e): 60% peanut oil fluorescence spectrum before de-scattering; (f): 60% peanut oil fluorescence spectrum after de-scattering; (g): 40% peanut oil fluorescence spectrum before de-scattering; (h): 40% peanut oil fluorescence spectrum after de-scattering; (i): 20% peanut oil fluorescence spectrum before de-scattering; (j): 20% peanut oil fluorescence spectrum after de-scattering; (k): Soybean oil fluorescence spectrum before de-scattering; (l): Soybean oil fluorescence spectrum after de-scattering

图2

Fig.2

Figure Option ViewDownloadNew Window

图2 EEM光谱平滑前后对比图 (a): 花生油EEM平滑前; (b): 花生油EEM平滑后; (c): 80%花生油EEM平滑前; (d): 80%花生油EEM平滑后; (e): 60%花生油EEM平滑前; (f): 60%花生油EEM平滑后; (g): 40%花生油EEM平滑前; (h): 40%花生油EEM平滑后; (i): 20%花生油EEM平滑前; (j): 20%花生油EEM平滑后; (k): 大豆油EEM平滑前; (l): 大豆油EEM平滑后Fig.2 EEM spectra from before and after smoothing (a): Peanut oil EEM before smoothing; (b): Peanut oil EEM after smoothing; (c): 80% peanut oil EEM before smoothing; (d): 80% peanut oil EEM after smoothing; (e): 60% peanut oil EEM before smoothing; (f): 60% peanut oil EEM after smoothing; (g): 40% peanut oil EEM before smoothing; (h): 40% peanut oil EEM after smoothing; (i): 20% peanut oil EEM before smoothing; (j): 20% peanut oil EEM after smoothing; (k): Soybean oil EEM before smoothing; (l): Soybean oil EEM after smoothing

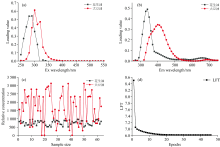
PARAFAC是利用最小二乘算法实现的一种多维数据基于三线性模型分解算法, 使用PARAFAC对EEM光谱数据三线性分解要进行降维和特征提取, 残差分析法和半劈裂分析(Split-half analysis)结合方差解释, 最终确定样品组分并验证平行因子模型的有效性^[24]。 需要特别说明是, 所谓的“ 组分” 是荧光信号接近的物质(共因子)。 因此, 不需要进行降维和特征提取, 残差分析法和半劈裂分析(Split-half analysis)结合方差解释确定样品组分。 可以确定组分数为2。 经过PARAFAC 处理后, 得到了特征荧光组分的波长范围, 并通过载荷图确定了相应组分的最大激发和发射波长, 从图3(a, b)可以看出激发/发射波长为290/340 nm是花生油; 激发/发射波长为300/400 nm是大豆油。 图3(c)为相对浓度矩阵, 可以获得每个样本的浓度得分, 如此便可以得到伪花生油中花生油的含量。 图3(d)为迭代图, PARAFAC模型迭代了48次, 损失函数(loss function, LFT)值收敛。 PARAFAC的训练集, 测试集, 全部数据的回归系数R²分别为0.756, 0.895, 0.898。 PARAFAC模型预测花生油含量偏差在± 15%以内的样本为74.6%, 偏差在± 10%为61.9%, 偏差在± 5%为14.3%。 PARAFAC的误差函数值见表1, 训练集、 测试集和全部数据的MAD、 MSE、 RMSE均较大, 预测结果并不理想。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 平行因子模型分析图 (a): 激发光载荷图; (b): 发射光载荷图; (c): 相对浓度; (d): 迭代曲线Fig.3 PARAFAC model analysis diagram (a): Loading diagrams of the excitation spectrum; (b): Loading diagrams of emission spectrum; (c): The relative concentration; (d): Iterative curve

表1

Table 1

表1(Table 1)

表1 PARAFAC模型误差函数值 Table 1 PARAFAC model error function value 训练集 测试集 全部数据 MAD 11.527 10.498 11.217 MSE 189.585 179.774 186.626 RMSE 13.769 13.407 13.661

表1 PARAFAC模型误差函数值 Table 1 PARAFAC model error function value

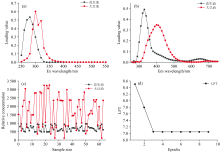
ATLD是基于三线性分析更高效的一种算法, 根据样品分解出来的组分轮廓进行定量分析^[25]。 同样, 与PARAFAC算法相似, 组分数可以确定为2。 从图4(a, b)可以看出激发/发射波长为290/340 nm是花生油激发/发射波长为300/400 nm是大豆油。 ATLD的组分解析结果与PARAFAC的相同。 图4(c)为相对浓度矩阵, 获得每个样本的浓度得分, 也可以得到伪花生油中花生油的含量。 图4(d)为迭代图, ATLD模型迭代了9次, LFT值收敛。 相较于PARAFAC的迭代次数, ATLD的收敛速度明显更快。 ATLD的训练集, 测试集, 全部数据的R²分别为0.895, 0.826, 0.941。 ATLD模型预测花生油含量偏差在± 15%以内的样本百分比为93.65%, 偏差在± 10%为79.3%, 偏差在± 5%为50.8%。 ATLD模型预测效果优于PARAFAC模型。 ATLD模型的误差函数值见表2, ATLD模型的误差函数值除测试集的MSE外, 训练集、 测试集和全部数据的MAD、 MSE、 RMSE比PARAFAC模型小, 预测结果也并不理想。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 交替三线性分解模型分析图 (a): 激发光载荷图; (b): 发射光载荷图; (c): 相对浓度; (d): 迭代曲线Fig.4 ATLD model analysis diagram (a): Loading diagrams of the excitation spectrum; (b): Loading diagrams of emission spectrum; (c): The relative concentration; (d): Iterative curve

表2

Table 2

表2(Table 2)

表2 ATLD模型误差函数值 Table 2 ATLD model error function value 训练集 测试集 全部数据 MAD 5.395 9.933 6.764 MSE 63.672 211.954 108.392 RMSE 7.979 14.558 10.411

表2 ATLD模型误差函数值 Table 2 ATLD model error function value

对EMM进行消除拉曼和瑞利散射, 平滑处理后的数据进行小波分解, 每个样本得到最低频段的小波包系数为199个, 以小波包系数表征不同样本EEM光谱。

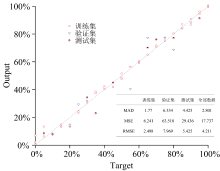
PLS是在20世纪70年代作为一种经济学工具发展起来, 后来作为一种统计学工具在需要领域被应用, 尤其是化学计量学和社会科学^[26]。 PLS在食品行业中已经获得了普及, 因为它能够通过多变量线性模型将两组不同性质的数据相关联起来, 能够在有多重共线性即自变量之间也存在线性关系的情况下对数据进行建模, 在样本数量小于预测变量数量的情况下同样可行^[27]。 PLS是一种多因变量对多自变量的一阶数据回归建模方法, 伪品中花生油的含量是因变量, 每个样本的最低频段小波包系数是自变量, 构建的WPD-PLS模型的训练集、 测试集与总体数据的回归系数R²分别为0.969, 0.907, 0.961。 图5为伪品中预测花生油含量训练集和测试集的真实值和预测值的对比图。 WPD-PLS算法模型的预测结果与真实值的偏差全部在± 15%以内, 偏差在± 10%的样本百分比为92%, 在± 5%为52%。 如图5所示, WPD-PLS算法模型训练集、 测试集和全部数据的MAD、 MSE、 RMSE均较小, 优于ATLD与PARAFAC模型。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 PLS回归曲线及误差函数Fig.5 PLS regression curve and error function value

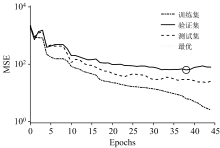
WPD分解EEM数据后, 重构的EEM数据为一阶数据, ANN构建的模型的训练曲线如图6, WPD-AAN算法模型的MSE值越小, 模型预测花生油含量试验数据的精确度越高。 当训练步数逐渐增加时, MSE逐渐趋近于误差的最优值。 WPD-ANN算法模型训练迭代到38次时, 训练集和测试集的MSE已低于验证集最优值, MSE为63.52; 说明该模型能够满足需求; 同时, 在验证集的MSE曲线增加之前, 测试集的MSE曲线未显著增加, WPD-ANN算法模型训练完成。 如图7所示, WPD-ANN算法模型的训练集、 验证集、 测试集和全部数据的MAD、 MSE、 RMSE均较小, 是4种算法模型中最优的。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 人工神经网络训练曲线Fig.6 ANN training curve

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 人工神经网络的回归曲线及误差函数值Fig.7 ANN regression curve and error function value

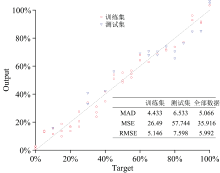
WPD-ANN模型预测伪品中花生油含量的训练集、 验证集、 测试集和全部数据预测结果与真实值的散点图如图7所示。 WPD-ANN算法模型的训练集、 验证集、 测试集与总体数据的回归系数R²分别为0.992、 0.925、 0.966和0.981, 表明WPD-ANN模型随机验证效果良好, WPD-ANN模型能很好地描述EEM和伪花生油中花生油含量的关系。 真实值与预测的数据点几乎都在直线Y=X附近, 表明伪品中花生油含量和WPD-ANN模型的预测值之间具有较好的兼容性。 WPD-ANN模型预测值与真实值的偏差全部在± 15%, 偏差在± 10%的样本百分比为93.6%, 偏差在± 5%为82.5%。 因此, 该WPD-ANN算法模型对伪花生油中花生油含量具有很强的预测能力且误差较小。 因此, WPD-ANN模型能够预测EEM与花生油含量之间的关系。

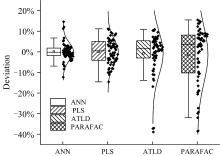
原始EEM数据通过三角形插值法去除了拉曼散射和瑞利散射, 进行PARAFAC与ATLD运算, ATLD明显所需内存大大减少, 提高运算的效率, 是迭代算法中收敛速度较快的一种算法。 通过WPD后, 进行PLS和ANN运算, PLS基于线性算法, 而ANN算法中使用激活函数, 基于非线性运算。 4种算法预测值与真实值的偏差箱线图和正态分布曲线图如图8, 箱线图具有一定的识别异常值的能力。 从图8表明, WPD -ANN算法模型偏差异常值为6个, WPD-PLS算法模型没有异常值, ATLD算法模型的异常值为6个, PARAFAC算法模型的异常值为3个。 产生异常值可能是由于不同批次的花生油和大豆油成分的差异造成的。 同时, 对于标准正态分布的样本, 异常值只占很小的比例。 如图8, WPD-ANN和WPD-PLS模型偏差的均值和中位数都在0%附近, 而ATLD和PARAFAC模型偏差的均值和中位数离0%较远。 PARAFAC, ATLD, WPD-PLS, WPD-ANN模型预测花生油含量偏差在± 15%以内的样本分别为74.6%, 93.65%, 100%, 100%; 偏差在± 10%分别为61.9%, 79.3%, 92%, 93.6%; 偏差在± 5%分别为14.3%, 50.8%, 52%, 82.5%。 原因为ATLD和PARAFAC都是基于求解三线性分量模型的算法, 在处理EEM数据时, 计算结果可能受到非线性因素的影响^[21], 例如高浓度物质与荧光强度不是线性关系。 ANN和PLS是基于WPD及数据重构后一阶数据回归建模, 由于的荧光光强为吸收的激发光光强和荧光效率的乘积, 荧光强度只有在低浓度时荧光物质浓度成正比, PLS是线性模型, 而ANN是非线性模型。 因此, WPD-ANN算法偏差最小, 是4种算法中最优的。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 4种算法偏差的箱式图及正态分布图Fig.8 Prediction deviation box and Normal distribution diagram of 4 algorithms