Seya-Namioka类型真空紫外光谱系统的研制和性能测试

引用本文

沈永才, 钮雨凡, 孔德峰, 叶扬, 张寿彪, 李大创, 谭名昇, 黄艳清, 赵志豪, 訾鹏飞, 张小辉, 文斐. Seya-Namioka类型真空紫外光谱系统的研制和性能测试[J]. 光谱学与光谱分析, 2024,44(8): 2158-2165.
SHEN Yong-cai, NIU Yu-fan, KONG De-feng, YE Yang, ZHANG Shou-biao, LI Da-chuang, TAN Ming-sheng, HUANG Yan-qing, ZHAO Zhi-hao, ZI Peng-fei, ZHANG Xiao-hui, WEN Fei. Development and Performance Test of a Seya-Namioka Vacuum Ultraviolet Spectroscopy System[J]. Spectroscopy and Spectral Analysis, 2024,44(8): 2158-2165.
Doi:10.3964/j.issn.1000-0593(2024)08-2158-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

Seya-Namioka类型真空紫外光谱系统的研制和性能测试

沈永才¹, 钮雨凡¹, 孔德峰², 叶扬^2,^*, 张寿彪³, 李大创¹, 谭名昇², 黄艳清⁴, 赵志豪⁵, 訾鹏飞³, 张小辉⁵, 文斐³

1.合肥师范学院物理与材料工程学院, 安徽合肥 230601

2.合肥综合性国家科学中心能源研究院(安徽省能源实验室), 安徽合肥 230031

3.中国科学院合肥物质科学研究院等离子体物理研究所, 安徽合肥 230031

4.衡阳师范学院物理与电子工程学院, 湖南衡阳 421008

5.合肥工业大学计算机与信息学院, 安徽合肥 230009

*通讯作者 e-mail: yeyang@ie.ah.cn

作者简介: 沈永才, 1987年生, 合肥师范学院物理与材料工程学院副教授 e-mail: syc@ipp.ac.cn

收稿日期: 2023-08-19 修回日期: 2024-03-12

基金: 国家自然科学基金项目(12205072), 安徽高校协同创新项目(GXXT-2021-029, GXXT-2021-014), 合肥综合性国家科学中心能源研究院项目(19KZS205, 21KZS202), 合肥师范学院2022年度引进高层次人才科研启动基金项目(2022rcjj07), 合肥师范学院横向课题(HXXM2022019, HXXM2022051)资助

摘要

为了满足磁约束核聚变领域的杂质测量要求, 研制了一套Seya Namioka真空紫外光谱仪。该光谱仪的主要部件是可调宽度的入射狭缝、凹面光栅和探测器。光谱仪的光通量通过可调节宽度的入射狭缝来调节, 入射狭缝宽度可以在10~1 000 μm范围内调节。分光元件选用线密度为1 200 lines·mm^-1的凹面全息光栅。光栅表面涂有铝(Al)和氟化镁(MgF₂), 以提高衍射效率。光栅的可使用波段为50~460 nm, 针对其中的50~250 nm波段进行光路优化设计。选用深度制冷背照式电荷耦合器件(CCD)作为光谱仪的探测器。通过转动光栅转台旋转光栅来改变衍射角, 实现50~250 nm范围内的光谱观测。基于凹面光栅的参数, 确定了具体光路, 并分析了波长随光栅旋转角度的变化关系及不同波长处的线色散率。基于凹面光栅成像理论, 对系统的光谱分辨率进行了计算分析。通过分析不同出射臂下的光谱分辨率, 确定最优出射臂为205 mm。在出射臂为205 mm、入射狭缝为20 μm的情况下, 分析了入射狭缝宽度、像素大小、像差和衍射极限对光谱分辨率影响。结果表明: 衍射极限对光谱分辨率的影响最小, 基本上可以忽略不计, 出射狭缝的宽度对光谱分辨率有较大贡献, 大约为0.09~0.10 nm, 且在50~250 nm波长范围内缓慢增加。分析了不同入射狭缝宽度(10~80 μm)下光谱分辨率, 光谱分辨率随狭缝宽度呈递增趋势, 变化范围为0.10~0.32 nm, 当狭缝宽度达到80 μm时, 光谱分辨率已经变的较差, 不利于高分辨线辐射光谱测量。在实际测量中, 应该综合考虑光通量和光谱分辨率需求。采用低压汞灯和微波等离子体光源进行波长校准和性能测试。基于零阶光谱和汞灯的特征光谱Hg Ⅰ (185 nm)对光谱仪进行了波长标定。通过Hg Ⅰ(185 nm)谱线的高斯拟合分析, 得到仪器在185 nm处的光谱分辨率为0.124 3 nm, 与理论计算值接近。通过实验与理论计算对比不同出射臂下的Hg Ⅰ (185 nm)光谱分辨率, 验证了仪器在出射臂为205 mm处获得最佳光谱分辨能力。利用微波等离子体放电光源装置对光谱仪进行了进一步的性能测试, 基于光源发射的氮、氧和氦线的测量, 验证了光谱仪在50~250 nm波长范围内具有良好的探测能力。

关键词: 真空紫外光谱仪; 凹面全息光栅; 光谱分辨率; 波长标定

中图分类号:O433.1 文献标志码:A

Development and Performance Test of a Seya-Namioka Vacuum Ultraviolet Spectroscopy System

SHEN Yong-cai¹, NIU Yu-fan¹, KONG De-feng², YE Yang^2,^*, ZHANG Shou-biao³, LI Da-chuang¹, TAN Ming-sheng², HUANG Yan-qing⁴, ZHAO Zhi-hao⁵, ZI Peng-fei³, ZHANG Xiao-hui⁵, WEN Fei³

1. School of Physics and Materials Engineering, Hefei Normal University, Hefei 230601, China

2. Institute of Energy, Hefei Comprehensive National Science Center, Hefei 230031, China

3. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China

4. School of Physics and Electronic Engineering, Hengyang Normal University, Hengyang 421008, China

5. School of Computer Science and Information Engineering, Hefei University of Technology, Hefei 230009, China

*Corresponding author

Abstract

Impurity behavior study is very important in magnetic confined fusion research as impurity may cause the dilution of fuel ions, affect the power balance, and degrade plasma performance. Spectroscopic diagnostic is important for impurity measurement and transport study in fusion devices. Spectroscopy in the vacuum ultraviolet (VUV) range offers a useful tool for investigating impurity radiation from low-temperatureareasof edge tokamak plasma. To meet the impurity measurement requirement in fusion research, a Seya-Namioka spectrometer was designed, and the main parts of the spectrometer are adjustable width incident slits, concave gratings, and a detector). The luminous flux of the spectrometer is adjusted through an adjustable width of the incident slit, which is of the linear guide type. The position of the incident slit baffle is adjusted through the linear guide to achieve slit width adjustment. The grating surface is coated with aluminum (Al) and magnesium fluoride (MgF₂) to enhance the refractive efficiency. The usable wavelength range of the grating is 50~460 nm, and the optical path optimization design is carried out for the 50~50 nm wavelength range. The spectrometer's detector was chosen as a deeply cooled back-illuminated charge-coupled device (CCD). By turning the grating turntable to rotate the grating and change the diffraction angle, spectral observations in the 50~250 nm range can be achieved. Based on the parameters of the concave grating, the specific optical path was determined, and the relationship between wavelength and grating rotation angle, as well as the line dispersion rate at different wavelengths, was analyzed. According to the theory of concave grating imaging, the spectral resolution of the system was calculated and analyzed. The optimal exit arm was determined to be 205 mm by analyzing the spectral resolution under different exit arms. The effects of incident slit width, pixel size, aberration, and diffraction limit on spectral resolution were analyzed with an exit arm of 205 mm and an incident slit of 20 μm. The main contributions to the spectral resolution are the entrance slit width, pixel size, aberration, and diffraction limit. The diffraction limit has the smallest effect on spectral resolution, which can be ignored. Due to the size of the detector pixel, the width of the exit slit has a great impact on the spectral resolution, which remains at about 0.09~0.10 nm and increases slowly in the 50~250 nm wavelength range. The total spectral resolution is between 0.121 nm and 0.122 nm. The width of the incident slit will be adjustable from 10 to 1 000 μm, depending on the intensity of the incident light. The wider the width of the incident slit, the worse the overall spectral resolution will be. In actual measurement, the luminous flux and spectral resolution should be considered. Wavelength calibration and performance tests were performed by using a low-pressure mercury lamp and microwave plasma light source. The wavelength calibration of the spectrometer can be completed based on the zero-order spectrum and the characteristic wavelength of the mercury lamp (Hg Ⅰ 185 nm). The zero-order spectrum position is defined as the diffraction angle zero position. The angular position of Hg Ⅰ 185 nm in the spectrometer is determined according to the formula. The spectral resolution was 0.124 3 at 185 nm by Gauss fitting of the Hg Ⅰ (185 nm) spectral line, which is close to the calculated value. By comparing the spectral resolution of Hg Ⅰ 185 nm under different exit arms through experiments and theoretical calculations, it was further verified that the instrument achieved the best spectral resolution at the exit-arm length of 205 mm. Further performance tests of the spectrometer were carried out using a microwave plasma discharge light source device. It has been verified that the spectrometer has good detection ability in the 50~250 nm wavelength range, based on observing nitrogen, oxygen, and helium lines emitted by microwave plasma light sources.

Keyword: Vacuum ultraviolet spectrometer; Concave holographic grating; Spectral resolution; Wavelength calibration

文章图片

引言

在磁约束核聚变托卡马克装置及托卡马克加料紧凑环(CTI)装置中, 对杂质行为及输运研究, 并探索杂质屏蔽的方法对磁约束核聚变装置实现稳态放电具有重要的意义^[1]。目前, 对杂质行为的研究是基于杂质光谱信息来分析, 通过特定波段的光谱诊断系统来测量一个或几个杂质的电离态线辐射光谱, 进一步估算杂质浓度及评估其对聚变装置放电的影响。在大型磁约束聚变装置中, 国内外主要是通过极紫外光谱诊断^{[2, 3]}和真空紫外光谱(VUV)诊断系统^{[4, 5, 6, 7, 8, 9, 10]}来监测杂质行为。东方超环(EAST)紧凑环装置作为EAST未来芯部加料的装置, 已完成初步研制^[11], 发展合适的杂质行为研究诊断是十分必要的。国内外在该类型装置上开展杂质测量和研究的报道极少。 EAST紧凑环温度在eV量级, 与EAST边界等离子体温度相近。该温度下, 可考虑采用真空紫外光谱诊断进行杂质行为监测。

在真空紫外光谱仪器中, Seya-Namioka结构的单色仪^[12]或光谱仪具有结构简单、布局紧凑的特点, 被广泛应用于同步辐射加速器等大型实验装置中^{[13, 14]}。该结构的光谱系统中, 入射和出射狭缝的位置不变, 让凹面光栅绕其垂直过顶点的轴转动, 在探测位置就可以获得不同波长的光谱。国内的磁约束核聚变装置上的真空紫外光谱仪主要是基于McPherson Model公司生产的单色仪^{[7, 8]}主体基础上研制出来的, 采用探测器和狭缝位置固定, 旋转光栅的方式进行波长扫描。在HL-2A装置上, 利用该类型光谱仪获得了碳、氧、氮等多种杂质的特征谱线^[7]。光谱分辨率与出射臂位置有关, 通过优化出射臂位置可以一定程度上提高特定波段的光谱分辨率。国外公司生产的光谱仪其光栅核心参数一般不告知用户, 且采用固定的出射臂, 光谱仪光路是针对整个波段的优化设计, 无法从理论和实验上探究所需特定波段最优光谱分辨率所对应的条件。本研究光谱仪是基于已知的凹面光栅参数进行设计, 从凹面光栅成像理论分析所需波段光谱分辨率影响因素, 并结合实验探索该类型光谱仪分辨率的优化设计方案。所采用光栅为凹面全息光栅, 相比于机刻光栅, 全息光栅具有较小的杂散光和像差矫正等优点, 非常适合研制高性能的真空紫外光谱系统。针对EAST及其紧凑环装置现有参数条件和可用观测空间极为有限的情况, 为满足杂质行为测量及输运研究的基本需求, 研制一套基于凹面全息光栅作为分光元件、背照式大阵面CCD作为探测器件的真空紫外光谱仪。该系统的优化观测波长为50~250 nm, 波长分辨率约为0.12 nm。采用低压汞灯和微波等离子体光源光谱对光谱仪进行波长标定和性能测试, 验证仪器性能。

1 光谱仪设计

Seya-Nomioka类型光谱系统是基于Seya-Nomioka光栅的分光原理而实现光谱测量的, 如图1所示是Seya-Nomioka凹面光栅的光学原理图。当入射光入射到凹面光栅上时, 入射角为α₀的入射光线经光栅分光并将波长为λ₀的单色光出射到出射狭缝处。当转动光栅时, 入射光线和出射光线不变, 由于光栅的中心轴发生变化, 入射角(图中由α₀变为α'₀)和出射角(图中由β₀变为β'₀)也发生变化, 最终导致输出波长发生改变(图中由λ₀变为λ'₀)。图2是真空紫外光谱诊断系统的光路示意图。入射狭缝、光栅中点和出射狭缝位于罗兰圆上, 罗兰圆与光栅及成像面垂直。光从入射狭缝照射到凹面全息光栅上, 经光栅反射到出射狭缝或成像面。若在狭缝处采用微通道板作为探测器, 该光路系统即为Seya-Namioka单色仪。若在成像面采用面阵型探测器作为光谱接收器, 该光路系统即为光谱仪。分光元件采用公称线密度为1 200 g· mm^-1相差校正凹面全息光栅, 其焦距r是200 mm, 曲率半径为224 mm, 光栅尺寸为40 mm× 45 mm。入射狭缝到光栅中心的距离r₁=181 mm, 光栅中心到出射狭缝的距离设置为r₂=205 mm。狭缝位置及成像面位置固定, 通过光栅转动, 实现不同波长光谱的测量。如用2k表示入射光轴和出射光轴的夹角, 为64° 。 θ 表示光栅旋转角度, α 和β 分别是入射角和出射角, 可以得到如式(1)关系^[15]

$2 k = α + β = \cos nst, α = k + θ, β = θ - k$ (1)

	Figure Option View Download New Window
	图1 Seya-Nomioka光栅的光学原理图Fig.1 Optical principle of the Seya-Nomioka grating

	Figure Option View Download New Window
	图2 真空紫外光谱诊断系统光学示意图Fig.2 Optical schematic diagram of the vacuum ultraviolet spectroscopy diagnostic system

由光栅方程

$mλ = σ (\sin α + \sin β)$ (2)

式(2)中, m为谱线级次, σ 为光栅常数, 即光栅刻线的间距。

可以得到出射狭缝位置的波长λ 和光栅旋转角度θ 的关系为

$λ = (2 σ / m) \cos k \sin θ$ (3)

可以计算出出射狭缝位置的光谱线色散率为式(4)

$\frac{d λ}{d x} = \frac{σ \cos β}{mr}$ (4)

图3是光谱仪的设计结构图, 进光口和出光口位置固定, 分别配置狭缝和探测器。光栅表面采用铝(Al)和氟化镁(MgF₂)复合涂层来增强折射效率。光栅安装在光栅转移台上, 光栅转台核心部件为旋转导入器, 导入器下方为步进电机, 步进电机与导入器间通过联轴器实现软连接。通过圆形编码器编程实现步进电机角度反馈控制, 通过强磁耦合带动旋转轴转动, 旋转轴内轴接在真空室内, 该结构类型一定程度上降低了真空密封泄露风险。导入器可实现360° 范围转动, 角度重复定位精度小于± 10″, 全波段的光谱观测可以通过转动光栅转台带动光栅转动, 从而改变衍射角度来实现。光谱仪的通光量大小通过可调宽度的入射狭缝来调节, 该光谱仪入射狭缝宽度在10~1 000 μ m范围内可调。具体实验中可结合等离子体实际情况调节大小, 在满足光亮度的情况下可以适当优化光谱分辨率。

	Figure Option View Download New Window
	图3 真空紫外光谱诊断系统设计结构图Fig.3 Design structure diagram of the vacuum ultraviolet spectroscopy diagnostic system

根据选用的光栅, 结合式(1)— 式(4), 可以计算出在配备1 200 g· mm^-1光栅时出射狭缝位置的一阶谱波长λ₀随光栅旋转角度θ 的变化关系以及输出不同波长谱线时的线色散率, 结果分别如图4(a)和(b)所示。在50~250 nm波长范围内, 出射狭缝位置的线色散率介于3.6~3.9 nm· mm^-1之间, 且随波长增加而增加。

Figure Option
View Download New Window

图4 光谱仪相关参数计算结果
(a): 出射狭缝位置波长随光栅旋转角度变化关系; (b): 出射狭缝位置光栅谱线色散率随波长变化; (c): 单次观测波长范围随中心波长变化关系Fig.4 Calculation results of spectrometer related parameters
(a): The relationship between the wavelength of the exit slit position and the rotation angle of the grating; (b): Variation of dispersion of grating spectral line at exit slit position with wavelength; (c): The relationship between the wavelength range of a single observation and the variation of the central wavelength

探测器选用Andor公司生产的用于真空的二维CCD器件, 像素数1 024× 256, 其感光芯片尺寸为26.7 mm(水平方向)× 6.7 mm(竖直方向), 探测器感光芯片水平方向用于波长观测, 可以获得较大的单次波长观测范围。考虑到光谱仪所探测波段在空气中极易衰减, 仪器需在真空状态下工作, 探测器在真空环境中可采用深度制冷模式, 温度可降至-60° 来减少噪声。考虑到线色散率随观测波长有所变化, CCD探测器在不同波长位置获得的单次波长范围也有所不同, 如图4(c)所示。如在中心波长为100 nm时, 单次观测波长为87 nm。总之, 至少需要转动三次光栅, 才可实现全优化波段(50~250 nm)覆盖。

凹面全息光栅成像系统的光谱分辨率主要与狭缝宽度、像差以及衍射极限^{[16, 17, 18]}等因素有关。入射和出射狭缝对光谱分辨率的影响可以表示为

$Δ λ_{s 1} = \frac{σ S_{1} \cos α}{n r_{1}}$ (5)

$Δ λ_{s 2} = \frac{σ S_{2} \cos β}{n r_{2}}$ (6)

式(5)和式(6)中, S₁为入射狭缝的宽度(入射狭缝宽度设计值为10~1 000 μ m可调), S₂为出射狭缝的宽度, 由探测器单个像元宽度代替。

像差对光谱分辨率的影响可以表示为

$Δ λ_{A} = \frac{1}{nσ} (m F_{20} + \frac{3}{2} w^{2} F_{30} + \frac{1}{2} l^{2} F_{12} + \frac{1}{2} w^{3} F_{40} \dots)$ (7)

式(7)中, w和l分别为光栅的长和宽, F₂₀为离焦, F₃₀为彗形像差, F₁₂为像散慧差, F₄₀为球面像差。对于凹面衍射光栅, 式(7)4项是计算像差必须要考虑的, 更高阶的像差对光谱分辨率的影响可以忽略。若将式(7)4项对光谱分辨率的影响单独考虑, 分别命名为Δ λ _A₁、 Δ λ _A₂、 Δ λ _A₃和Δ λ _A₄, 则

$Δ λ_{A 1} = \frac{w}{nσ} F_{20} = \frac{w}{nσ} [T (r_{1}, α) + T (r_{2}, α)]$ (8)

$Δ λ_{A 2} = \frac{3 w^{2}}{2 nσ} F_{30} = \frac{3 w^{2}}{2 nσ} [\frac{T (r_{1}, α)}{r_{1}} \sin α + \frac{T (r_{2}, β)}{r_{2}} \sin β]$ (9)

$Δ λ_{A 3} = \frac{l^{2}}{2 nσ} F_{12} = \frac{l^{2}}{2 nσ} [\frac{S (r_{1}, α)}{r_{1}} \sin α + \frac{S (r_{2}, β)}{r_{2}} \sin β]$ (10)

$Δ λ_{A 4} = \frac{w^{3}}{2 nσ} F_{40} = \frac{w^{3}}{2 nσ} [\frac{4 T (r_{1}, α)}{r_{1}^{2}} si n^{2} α - \frac{T^{2} (r_{1}, α)}{r_{1}} + \frac{4 T (r_{2}, β)}{r_{2}^{2}} si n^{2} β - \frac{T^{2} (r_{2}, β)}{r_{2}} - 8 a_{40} (\cos α + \cos β)]$ (11)

式(8)— 式(11)中的

$T (r_{1}, α) = \frac{co s^{2} α}{r_{1}} - 2 a_{20} \cos α$ (12)

$T (r_{2}, β) = \frac{co s^{2} α}{r_{1}} - 2 a_{20} \cos β$ (13)

$S (r_{1}, α) = \frac{1}{r_{1}} - 2 a_{20} \cos α$ (14)

$S (r_{2}, α) = \frac{1}{r_{2}} - 2 a_{20} \cos β$ (15)

$a_{20} = \frac{1}{2 R}$ (16)

$a_{02} = \frac{1}{2 ρ}$ (17)

$a_{40} = \frac{1}{8 R}$ (18)

式(8)— 式(18)中, R为光栅的子午线半径, ρ 为光栅的曲率半径。由于光栅表面为球面, R和ρ 相等, 均为224 mm。

衍射极限对光谱分辨率的影响可以表示为

$Δ λ_{D} = \frac{λ}{nN}$ (19)

式(10)中, N为光栅的总刻槽数。

结合式(8)— 式(19), 光谱系统的光谱分辨率可以表示为式(20)

$Δ λ = \sqrt[]{Δ λ_{S 1}^{2} + Δ λ_{S 2}^{2} + Δ λ_{A}^{2} + Δ λ_{D}^{2}}$ (20)

由像差引起的光谱分辨率由四项构成[参见式(7)— 式(11)], 在代入光谱系(20)统相关硬件参数, 即可计算得到相关分辨率。此处, 光谱系统的硬件参数主要包括光栅刻槽数N=108 000、光栅曲率半径R=224 mm、光栅长w=45 mm和宽l=40 mm、入射狭缝宽度S₁=20 μ m和出射狭缝宽度S₂=26 μ m, 计算结果如图5所示。图5(a)显示的是50~250 nm波段, 离焦、彗形像差、像散慧差和球面像差对像差光谱分辨率的影响, 总光谱分辨率的影响在0.007~0.009 nm之间, 且随波长增加而增加。总光谱分辨率与入射、出射狭缝宽度、像差以及衍射极限有关[参见式(20)], 计算结果见图5(b)所示。其中衍射极限对光谱分辨率影响最小, 基本可以忽略。受限于探测器像元尺寸, 出射狭缝宽度对光谱分辨率影响较大, 其对分辨率影响保持在0.09~0.10 nm且在50~250 nm波段缓慢增加。总光谱分辨率在50~250 nm波段为0.121~0.122 nm。入射狭缝宽度在10~1 000 μ m范围内可调, 狭缝越宽, 总的光谱分辨率越差。

Figure Option
View Download New Window

图5 光谱分辨率计算结果
(a): 离差、彗形像差、像散慧差和球面像差对光谱分辨率的影响; (b): 入射狭缝、出射狭缝宽度、像差以及衍射极限对光谱分辨率的影响Fig.5 Spectral resolution calculation results
(a): The influence of aberration, comet aberration, astigmatic aberration and spherical aberration on aberration spectral resolution; (b): The influence of the width of the incident slit, the exit slit, the aberration and the diffraction limit on the spectral resolution

如图6为不同入射狭缝宽度(10~80 μ m)下光谱分辨率的计算结果, 在此入射狭缝变化范围, 光谱分辨率变化范围为0.10~0.32 nm, 当狭缝宽度达到80 μ m时, 光谱分辨率已经变的较差, 不利于高分辨率线辐射光谱测量。实际测量时, 要兼顾光通量和光谱分辨率这两个指标。在光通量满足测量的情况下, 适当优化光谱分辨率。

	Figure Option View Download New Window
	图6 入射狭缝宽度对光谱仪分辨率的影响Fig.6 The influence of incident slit width on spectral resolution

基于以上凹面光栅理论可知, 探测器的安装位置决定了出射壁r₂的大小, r₂会影响整体分辨率, 经过凹面光栅参数初步得到的最佳r₂值在200 mm附近。进一步在入射狭缝为20 μ m, 不同r₂(199~210 mm)值下得到光谱分辨率的设计值见图7所示。结果显示, 50~120 nm波段, 最佳分辨率对应的r₂为204 mm, 在120~250 nm波段, 最佳分辨率对应的r₂为205 mm。考虑整个波段分辨率最佳所对应的r₂应为205 mm。因此, 仪器的出射臂设置为205 mm。

	Figure Option View Download New Window
	图7 不同出射臂r₂(199~210 mm)对应的光谱分辨率Fig.7 Spectral resolution for different exit-arm length (199~210 mm)

2 光谱仪波长标定及性能测试

光谱仪在测量时, 探测器给出的是像元位置, 需要找出像元序号与波长的对应关系, 并将像元转化成对应的波长, 此过程即为波长标定过程。波长标定常采用的方法包括峰值法、多项式拟合, 参数拟合法^[19]等。对于本研究中的光谱仪, 波长标定采用的光源是低压汞灯。低压汞灯特征谱线Hg Ⅰ (185 nm)位于紫外波段, 标定可结合零级光谱和汞灯特征波长光谱Hg Ⅰ (185 nm)来完成。定义零级谱中心位置(对应探测器像素序号为512)为光栅旋转角度0位置, 采用光电门限位器定标0位置。然后结合式(3)初步定出Hg Ⅰ (185 nm)在光谱仪中的角度位置。再结合标定波长位置角度与特征波长光栅旋转角度及像元的对应关系来进行波长标定, 该关系可以表示为^[20]

$θ_{λ} = θ_{C} + \frac{(P_{λ} - P_{C}) S_{2}}{R \sin θ_{C}}$ (21)

式(21)中, θ _C为特征波长对应的角度, P_C为特征波长对应的像元, P_λ为待标定波长处的像元。

再将式(21)代入式(3)即可得到待标定像元处的波长。光栅转台在旋转多次会带来累积误差, 可通过监测0角度对应的零级谱中心位置偏离像素点进行修正。将Hg Ⅰ (185 nm)进行高斯拟合获得半高全宽(full width at half maximum, FWHM), 在入射狭缝为20 μ m的情况下, 得到该光谱仪测量的Hg Ⅰ (185 nm)的光谱分辨能力为0.124 3 nm(见图8所示), 这与图5(b)计算结果(约为0.122 0 nm)非常接近。

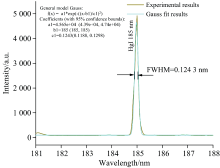	Figure Option View Download New Window
	图8 基于低压汞灯标准光谱(Hg Ⅰ 185 nm)高斯拟合Fig.8 Gauss fitting of Hg Ⅰ 185 nm based on low pressure mercury lamp standard spectrum

在不同出射臂(198~212 mm)下, 对实验测量的Hg Ⅰ (185 nm)谱线的半高全宽进行拟合, 并与理论计算值进行对比, 结果参见图9。结果表明, 光谱分辨率在出射臂为205 mm处均获得最佳值。实验和理论计算的光谱分辨率随出射臂长度的变化基本一致, 实验值略大于理论计算结果。

	Figure Option View Download New Window
	图9 Hg Ⅰ (185 nm)在不同出射臂r₂(198~212 mm)对应的半高全宽Fig.9 Spectral resolution of Hg Ⅰ (185 nm) for different exit-arm length (198~212 mm)

采用微波激发的气体等离子体无极放电光源(简称微波等离子体放电光源)装置^{[20, 21]}对光谱仪进行进一步波长标定及性能测试。微波等离子体放电光源装置在真空环境下进行, 采用机械泵和磁悬浮分子泵组合抽真空, 在主真空室真空度在10^-3 Pa量级即注入气体, 注入气体后通过控制气流速度将真空度维持在10^-2 Pa量级。本实验注入的气体为氦气, 因10^-3 Pa量级下装置壁材料吸附有氧气和氮气, 且装置目前未开展烘烤, 在实验中将会有氧气和氮气析出。因此, 考虑实验中等离子体主要的辐射光谱来源于氮、氧和氦。

微波气体等离子体在输入4 000~5 000 V高压、 300~400 mA电流的情况下产生, 采用光谱仪获得的氮、氧和氦在50~250 nm范围内的光谱见图10(a— d), 氮线主要来自于N Ⅱ 和N Ⅲ , 氧线来自于O Ⅰ — Ⅳ , 氦线来自于He Ⅱ 。具体的观测波长通过查找国际原子数据库(NIST)^[22]识别对应谱线, 通过对比不同波长标定的谱线以及NIST数据库谱线数据, 表明波长标定精度约为0.008 nm。

	Figure Option View Download New Window
	图10 微波等离子体光源在50~250 nm 波段光谱 (a): 50~100 nm; (b): 100~145 nm; (c): 145~195 nm; (d): 195~250 nmFig.10 Spectrum observations during 50~250 nm based on microwave plasma light sources (a): 50~100 nm; (b): 100~145 nm; (c): 145~195 nm; (d): 195~250 nm

图11(a, b)是时间长度为36 s微波等离子体放电中, O Ⅲ (105.867 nm)和He Ⅱ (121.517 nm)线辐射强度随时间演化。由图11可知, O Ⅲ 和He Ⅱ 线演化趋势一致, 在放电平稳期间(5~32.5 s)辐射强度变化较小, 证明光谱仪具备对线辐射光谱的实时测量功能, 且稳定性较好。

	Figure Option View Download New Window
	图11 光谱仪测量线辐射光谱强度随时间演化 (a): O Ⅲ (105.867 nm); (b): He Ⅱ (121.517 nm)Fig.11 Time evolutions of spectral line radiation intensities observed by the spectrometer (a): O Ⅲ (105.867 nm); (b): He Ⅱ (121.517 nm)

3 结论

基于凹面全息光栅, 研制了一台波长范围为50~250 nm的Seya-Namioka型光谱仪, 通过转动光栅实现不同波长光谱观测。根据凹面光栅参数确定具体光路, 并分析了不同波长处的线色散率。基于凹面光栅成像理论并结合光谱仪设计结构参数, 确定了光谱仪最佳出射臂。理论计算了离焦、彗形像差、像散慧差和球面像差对像差光谱分辨率的影响以及入射狭缝宽度、出射狭缝宽度、像差以及衍射极限对总的光谱分辨率的贡献, 并计算了不同入射狭缝宽度(10~80 μ m)下的光谱分辨率。在入射狭缝为20 μ m的情况下利用低压标准汞灯和微波等离子体放电光源对光谱仪进行波长标定和性能测试, 基于Hg Ⅰ (185 nm)谱线的高斯拟合结果表明光谱仪的光谱分辨率为0.124 3 nm@185 nm, 与计算值相近。结合实验和理论计算的185 nm处光谱仪在不同出射臂处的光谱分辨, 验证了205 mm为出射臂的最优设计值。利用微波等离子体放电光源观测到了50~250 nm波段的N、 O和He线, 通过多条标定谱线与NIST数据库对比, 表明波长标定精度较高。采用该系统, 可对核聚变装置中的杂质(如铁、铜、钨、碳、氧等)光谱进行高精度的实时测量, 并进一步对杂质浓度进行估算。该装置也可满足同步辐射装置相应波段光谱的测量需求。本研究提出的光谱仪的设计计算方案可为同类型光谱仪的研制提供参考。

参考文献

文献列表

[1]	Isler R C. Nuclear Fusion, 1984, 24(12): 1599. [本文引用:1]
[2]	Shen Yongcai, Lyu Bo, Du Xuewei, et al. Fusion Engineering and Design, 2013, 88(11): 3072. [本文引用:1]
[3]	Shen Yongcai, Du Xuewei, Zhang Wei, et al. Nuclear Instruments & Methods in Physics Research, 2013, 700(1): 86. [本文引用:1]
[4]	Field A, Fink R J, Dux R, et al. Review of Scientific Instruments, 1995, 66(12): 5433. [本文引用:1]
[5]	Maggi C F, Elder J D, Fundamenski W, et al. Journal of Nuclear Materials, 1997, 241-243(1): 414. [本文引用:1]
[6]	Morita S, Goto M. Reviews of Scientific Instrument, 2003, 74(3): 2036. [本文引用:1]
[7]	Cui Z, Morita S, Fu B, et al. Review of Scientific Instruments, 2010, 81(4): 043503. [本文引用:3]
[8]	HE Liang, ZHANG Hong-ming, CAO Jin-jia, et al(何梁, 张洪明, 曹锦佳, 等). Nuclear Fusion and Plasma Physics(核聚变与等离子体物理), 2021, 41(2): 110. [本文引用:2]
[9]	Li Y, Cheng Z F, Zhang X L, et al. Journal of Instrumentation, 2017, 12(6): C06043. [本文引用:1]
[10]	ZHANG Kai, ZHENG Dian-lin, DONG Chun-feng, et al(张凯, 郑典麟, 董春凤, 等). Nuclear Fusion and Plasma Physics(核聚变与等离子体物理), 2021, 41(2): 527. [本文引用:1]
[11]	Kong Defeng, Zhuang Ge, Lan Tao, et al. Plasma Science and Technology. 2023, 25: 065601. [本文引用:1]
[12]	MENG Zhu, TAN Xin, Bayanheshig, et al(孟竹, 谭鑫, 巴音贺希格, 等). Chinese Optics(应用光学), 2018, 11: 623. [本文引用:1]
[13]	WANG Qiu-ping, ZHANG Yun-wu, LIU Shao-yi, et al(王秋平, 张允武, 刘绍义, 等). Vacuum(真空), 1994, 4: 40. [本文引用:1]
[14]	XU Xiang-dong, LIU Zheng-kun, QIU Ke-qiang, et al(徐向东, 刘正坤, 邱克强, 等). Optics and Precision Engineering(光学精密工程), 2012, 12(1): 1. [本文引用:1]
[15]	Zhang Hongming, Lyu Bo, He Liang, et al. Plasma Science and Technology. 2020, 22: 084001. [本文引用:1]
[16]	XU Chao-yin(徐朝银). Optics and Engineering of Synchrotron Radiation(同步辐射光学与工程). Hefei: University of Science and Technology of China Press(合肥: 中国科技大学出版社), 2013: 85. [本文引用:1]
[17]	He Liang, Zhang Hongming, Lyu Bo, et al. Plasma Science and Technology, 2022, 24: 064003. [本文引用:1]
[18]	West J B, Padmore H A. Hand book on Synchrotron Radiation, Chapter 2-Optical Engineering, 1987: 21. [本文引用:1]
[19]	LI Xin, ZHANG Guo-wei, XUN Li-na, et al(李新, 张国伟, 寻丽娜, 等). Acta Optica Sinica(光学学报), 2008, 28(5): 902. [本文引用:1]
[20]	HUANG Tao, LU Hui, WANG Mao-bi, et al(黄桃, 卢辉, 王茂碧, 等). Vacuum Electronics(真空电子技术), 2013, 307(6): 73. [本文引用:2]
[21]	Xin Renxuan. Chinese Journal of Inorganic Analytical Chemistry, 2012, 2(4): 1. [本文引用:1]
[22]	Kramida A. Atomic Spectra Database From National Institute of Stand ards and Technology[EB/OL]. 2022. http://physics.nist.gov/PhysRefData/ASD/index.html [本文引用:1]

1984

0.0

... 引言在磁约束核聚变托卡马克装置及托卡马克加料紧凑环(CTI)装置中, 对杂质行为及输运研究, 并探索杂质屏蔽的方法对磁约束核聚变装置实现稳态放电具有重要的意义^[1] ...

2013

0.0