引用本文
李灵巧, 王卓健, 陈江海, 卢丰, 黄殿贵, 杨辉华, 李泉. 迁移成分分析结合直接校正的模型传递方法[J]. 光谱学与光谱分析, 2024,44(12): 3399-3405.
LI Ling-qiao, WANG Zhuo-jian, CHEN Jiang-hai, LU Feng, HUANG Dian-gui, YANG Hui-hua, LI Quan. A Model Transfer Method Based on Transfer Component Analysis and Direct Correction[J]. Spectroscopy and Spectral Analysis, 2024,44(12): 3399-3405.
Doi:10.3964/j.issn.1000-0593(2024)12-3399-07  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
迁移成分分析结合直接校正的模型传递方法
李灵巧1, 王卓健1, 陈江海1, 卢丰1, 黄殿贵2, 杨辉华3, 李泉2,*
1.桂林电子科技大学计算机与信息安全学院, 广西 桂林 541004
2.广西壮族自治区分析测试研究中心, 广西 南宁 530022
3.北京邮电大学人工智能学院, 北京 100876
*通讯作者 e-mail: coriah@163.com

作者简介: 李灵巧, 1986年生, 桂林电子科技大学计算机与信息安全学院副研究员 e-mail: 54pe@163.com

收稿日期: 2023-11-21 修回日期: 2024-05-25
基金: 国家自然科学基金项目(62262010), 桂林电子科技大学研究生创新项目(2023YCXS052)资助
摘要

近红外光谱因快速、 不破坏样品等优点, 被广泛应用。 近红外光谱仪之间存在一致性现象会导致主机模型预测其从机仪器光谱时准确度不够, 如果重新建模则会成本较高。 为解决上述问题, 提出了一种迁移成分分析直接校正算法(TCADS), 首先采用改进后的TCA算法对服从不同分布的主机光谱和从机光谱进行变换, 将其映射到高维的再生核希伯尔特空间, 再将两者的光谱矩阵进行降维, 最后对经过TCA变换后的主机光谱和从机光谱再次采用直接校正算法, 进一步提高模型传递性能。 该算法将非线性校正与线性校正相结合, 相比于传统的线性校正算法有效缓解了过校正问题, 具有较好的鲁棒性。 为验证算法有效性, 在公开数据集进行实验, 并与传统的直接校正法(DS)、 分段直接校正法(PDS)、 斜率偏差校正法(SBC)进行比较。 研究表明所提出的TCADS算法有效降低了不同仪器之间的光谱差异, 相比于传统的模型传递算法进一步提高了模型传递效果, 实现了主机上建立的近红外光谱模型在从机上共享。

关键词: 近红外光谱; 模型传递; 迁移学习; 迁移成分分析; 直接校正
中图分类号:O657.3 文献标志码:A
A Model Transfer Method Based on Transfer Component Analysis and Direct Correction
LI Ling-qiao1, WANG Zhuo-jian1, CHEN Jiang-hai1, LU Feng1, HUANG Dian-gui2, YANG Hui-hua3, LI Quan2,*
1. School of Computer Science and Information, Guilin University of Electronic Technology, Guilin 541004, China
2. Guangxi Zhuang Autonomous Region Center for Analysis and Test Research, Nanning 530022, China
3. School of Artificial Intelligence, Beijing University of Posts and Telecommunications, Beijing 100876, China
*Corresponding author
Abstract

Near-infrared spectroscopy has been widely used due to its high efficiency and non-destructive properties advantages. However, the consistency phenomenon between near-infrared spectrometers can lead to insufficient accuracy when the master model predicts the spectra of its slave instruments. If the calibration model is rebuilt based on the offset spectrum, it will lead to higher consumption. This paper proposes a transfer component analysis direct standardization (TCADS) algorithm to address the above issues.The algorithm initially employs an enhanced TCA algorithm to convert master and enslaved person spectra, which adhere to distinct distributions, by projecting them into high-dimensional reproducing kernel Hilbert space. Subsequently, it reduces the dimensionality of their spectral matrices. Finally, a direct standardization algorithm is reapplied to the master and slave spectra post-TCA transformation, further enhancing the model′s transfer performance. This algorithm combines nonlinear correction with linear correction, effectively alleviating the problem of overcorrection compared to traditional linear correction algorithms, and is robust. To verify the effectiveness of the algorithm, experiments were conducted on public datasets and compared with traditional direct standardization (DS), piecewise direct standardization (PDS), and slope and bias correction (SBC) methods. The experiment demonstrates that the TCADS algorithm proposed in this article efficiently minimizes spectral disparities between the master instrument and the slave instrument. This enhancement notably outperforms traditional model transfer algorithms, facilitating the effective sharing of near-infrared spectral models established on the master instrument to the slave instrument.

Keyword: Near-infrared spectroscopy; Model transfer; Transfer learning; Transfer component analysis; Direct standardization
引言

近红外光谱技术是一种快速、 高效、 绿色的检测方案, 已广泛应用于农业, 食品, 医药, 石油等领域定量或定性分析[1, 2, 3, 4]。 由于温度, 光源等外界条件以及不同仪器之间的差异, 主机上建立的模型不能很好地适用于从机上的样本, 导致模型失效[5]。 对从机样本重新建立模型则需花费较高的成本, 仍无法实现同一模型在不同仪器上共享[6]。 为解决此问题, 需要采用一些算法对模型进行校正, 从而提高模型在不同仪器上的泛化性能, 在近红外领域被称为模型传递或模型转移[7]。 目前广泛应用的模型传递算法有直接校正法(direct standardization, DS)[8]、 分段直接校正法(piecewise direct standardization, PDS)[9]以及斜率偏差校正法(slope and bias correction, SBC)[10]。 DS算法的先通过标样的主机光谱和从机光谱计算得到转换矩阵, 采用转换矩阵将从机新样本进行线性变换得到主机模型可以预测的光谱矩阵。 PDS在DS基础上引入窗口进行分段转换, 主机光谱的某波长点对应从机光谱在该波长点附近扩展形成的一个窗口, 计算得到该波长点的转换系数, 移动至下一个波长点进行计算, 最终所有波长点的转换系数构成了转换矩阵。 从机新样本借助转换矩阵得到映射后的光谱矩阵实现模型传递。 相比于关注整体信息的DS算法, PDS算法更加关注局部信息, 可以更好地对光谱的局部波长进行校正[11]。 这并不意味着PDS算法一定优于DS算法, 两者只是关注的重点不同, 要根据实际情况选取合适的算法。 Munnaf等[12]研究了DS和PDS对土壤模型传递的效果, 结果表明相比于PDS, 采用DS算法校正后模型的预测效果更好。 与DS和PDS算法对光谱矩阵进行校正不同, SBC算法是一种基于预测结果校正的模型传递算法, 假设主机模型直接预测从机数据的结果与真实结果存在一元线性关系, 在此基础上可以通过最小二乘法计算斜率和截距。 对于从机新样本可以使用计算好的斜率和截距校正预测的结果, 达到主机模型预测从机样本的效果。

以上算法和最近流行的深度学习算法被应用于光谱的建模分析[13], 都能提高模型的泛化能力。 解决了模型失效的问题。 这些算法均基于线性变换实现, 而不同仪器间可能存在非线性差异, 在一定程度上制约了模型传递效果的进一步提升, 因此需要尝试新的思路去解决模型传递中的难题。 由于迁移学习和模型传递具有天然相似性, 本研究尝试采用迁移学习进行模型传递。 迁移学习通常用于自然图片, 在光谱领域研究相对较少。 刘翠玲等[14]将迁移学习中的TCA[15]算法应用于食用油近红外光谱模型的迁移, 缓解了模型失效的问题, 而转移后的样本预测结果与理想结果仍存在一定差异, 传递后的模型仅能预测从机标样, 对从机新样本无法进行预测。 本工作提出了迁移成分分析直接校正算法(transfer component analysis direct standardization, TCADS), 由TCA算法获得启发, 并对TCA算法进行改进, 解决了模型无法递泛化到样本外的问题, 又加入了DS算法进行二次校正, 进一步提升了模型传递后的预测精度。 实验表明, TCADS算法相比于传统的DS, PDS, SBC算法模型传递的稳定性和传递效果均有所提升。

1 算法原理
1.1 迁移成分分析直接校正算法

TCADS算法首先采用改进后的迁移成分分析(TCA)算法进行映射, 映射后的数据服从同一分布, 再使用DS算法进行二次校正。 TCA基于特征的迁移学习方法, 核心任务是通过对特征进行变换完成迁移。 未迁移的源域和目标域的边缘分布有所不同, 即P(xS)≠ P(xT); 经过TCA特征映射Φ 使得映射后的数据可以满足P[Φ (xS)]≈ P[Φ (xT)], 达到源域和目标域之间的数据分布近似的目的。 由于未经过处理的主机光谱和从机光谱在原先的维度上不便于最小化数据间的距离, 因此可通过特征变换将两者变换到同一空间中计算最小距离, 采用最大均值差异(maximum mean discrepancy, MMD)度量特征变换后源域和目标域的均值之差, 并通过缩小MMD提高数据分布的相似性[见式(1)]

dist(X'src, X'tar)=1n1∑i=1n1Φ(xsrci)-1n2∑i=1n2Φ(xtari)H(1)

将MMD距离平方展开后采用核函数的形式计算映射, 引入了核矩阵K以及参数L, 见式(2)

K=Ksrc, srcKsrc, tarKtar, srcKtar, tarLij=1n12xi, xj∈Xsrc1n22xi, xj∈Xtar-1n1n2otherwise(2)

将MMD距离变换为矩阵的迹(trace)的形式进行运算[见式(3)]

trace(KL)-λtrace(K)(3)

采用降维构造结果, 并构造中心矩阵H以计算数据的散度从而维持数据的特征

H=In1+n2-1n1+n2iiT(4)

式(4)中, I为单位矩阵, n1和n2为源域和目标域的样本数量, i为n1+n2维的列向量。 经过核函数映射得到K, 再计算(KLK+μ I)-1KHK的前m个特征值, 可以得到变换后的源域和目标域数据拼接而成矩阵, 完成两个域之间的特征迁移。 当主机和从机采用标准样品进行TCA变换后, 可实现这批标准样品的模型传递, 而对于从机标准样品外的新样本数据仍无法进行传递。 本工作改进了传统的TCA, 使输出不再是经过变换后的源域和目标域, 而是得到一个变换矩阵A。 改进后的TCA算法根据标准样本得到变换矩阵A, 当有新的从机样本Xnew时, 将变换矩阵A与转置后的新样本光谱矩阵相乘得到映射矩阵Xtrans[见式(5)]

Xtrans=AXnewT(5)

对映射矩阵Xtrans进行L2范数归一化并转置为原先光谱矩阵的维度

Xstd=Xtrans‖Xtrans‖2T(6)

式(6)中, Xstd即为与标样服从同一分布的新样本光谱, 实现迁移后模型可以泛化到样本外。 为了进一步提高TCA的模型传递效果, 加入基于线性变换的DS算法。 由于TCA算法的原理是将主机光谱和从机光谱进行非线性映射, 因此在二次校正时应选择基于光谱矩阵进行校正的算法。 相比于PDS算法, 使用DS算法在校正时有更小的时间需求; 经过改进的TCA算法降维后特性波长点数目较少, 在此基础上使用通过窗口进行模型传递的PDS算法, 可能会忽略整体的光谱信息。 由于上述原因, 在改进的TCA算法校正后选取DS算法进行线性校正。 将标样经过TCA映射得到新的主机矩阵Xm和从机矩阵Xs, 通过从机光谱伪逆矩阵 Xs+获得转换矩阵F[见式(7)]

F=Xs+Xm(7)

采用转换矩阵F对已经过TCA校正后从机新样本进行二次映射, 得到最终的光谱矩阵Xres

Xres=XstdF(8)

式(8)中, Xres为经TCADS算法处理后的从机光谱矩阵, 可输入主机模型进行预测, 模型传递至此完成。 主机光谱数据和从机光谱数据经过TCA处理后, 二者的数据分布已经较为近似, 在此基础上采用传统的DS算法进行进一步校正, 改善了仅仅使用直接校正时可能带来的过校正问题, 同时也增强了仅采用 TCA 进行迁移的效果。 TCADS算法模型传递流程如图1所示。

图1 TCADS算法模型传递流程图Fig.1 The procedure of TCADS algorithm

TCADS是一种非线性校正结合线性校正的方案, 首先进行非线性校正, 并以MMD为度量将主机光谱与从机光谱映射到高维的空间。 不同于DS算法的从机向主机分布对齐, 这种非线性校正是将两者映射到一个全新的分布空间中, 可减缓DS算法带来的过校正问题; 采用线性校正, 使用DS算法在新的分布空间上二次校正进一步提高模型的预测精度。 TCADS将非线性与线性校正相结合, 理论上是一种较为鲁棒的算法, 以下通过实验验证这一结论。

1.2 实验数据集

为验证所提出的TCADS算法的模型传递效果, 实验采用了两个公开的数据集, 分别为Eigenvector Research公司提供的玉米数据集和药品数据集。此数据集分别从网址https://eigenvector.com/data/Corn/index.html和https://eigenvector.com/data/tablets/index.html下载获得。

1.2.1 玉米数据集

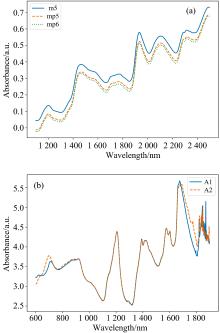
玉米数据集有80个样本, 含有四种成分作为预测标签, 分别是水分, 油脂, 蛋白质和淀粉。 每个样本分别由m5, mp5, mp6 三台近红外光谱仪测量共获得240条数据; 波长范围为1 100~2 498 nm, 光谱间隔为2 nm, 全谱共700个波长点。 选择m5作为主机, mp5和mp6作为从机进行模型传递, 对两台从仪器四种成分共计八个结果分别进行实验并讨论。

1.2.2 药品数据集

药品数据集有655个样本, 含有三种指标作为预测标签, 分别是质量, 硬度以及活性成分。 每个样本分别由A1, A2两台近红外光谱仪测量, 获得共计1 310个数据, 波长范围为600~1 898 nm, 光谱间隔为2 nm, 全谱共650个波长点。 将A1作为主仪器, A2作为从仪器进行模型传递, 取活性成分作为预测值。

1.3 样本划分

实验使用KS算法[16]进行样本划分, 其中采取80%的样本作为训练集, 20%作为测试集。 其中玉米数据集并未被划分, 因此采用KS算法以4:1划分为校正集和测试集进行模型训练和效果评估。 药品数据集被预先划分成了155个校正集, 40个验证集以及460个测试集。 为了提升模型的训练性能, 将药品数据集的三个子集进行合并, 再使用基于度量的KS算法对数据集以4:1重新划分为校正集和测试集。

1.4 模型传递方法的评价指标

实验采用决定系数(R2), 预测均方根误差(RMSEP), 光谱平均差异(ARMS)以及光谱校正率(Prcorrected)作为模型传递的评价指标。 R2和RMSEP常用来评估建模阶段校正模型的预测效果。 而在模型传递阶段, 除了R2和RMSEP两个指标来评估外, 还引入了ARMS以及Prcorrected来表征传递前后主机光谱和从机光谱浓度矩阵的相似性。 ARMS表征的是同一样本在不同光谱仪器测量下得到的光谱矩阵之间的差异, 仪器之间的差异越大, ARMS的值就越大。 Prcorrected表征的是经过模型传递后光谱的校正程度, Prcorrected越接近1则说明模型传递方法的效果越好。

R2=1-∑i=1n(y^i-yi)2∑i=1n(y̅-yi)2(9)

RMSEP=1n∑i=1n(y^i-yi)2)(10)

ARMS=1n∑i=1n1p∑λ=1p|S1λi-S2λi|(11)

Prcorrected=ARMSuncorrected2-ARMScorrected2ARMSuncorrected2(12)

式(9)和式(10)中, n为样本个数, yi为第i个样本的真实值, y^i为第i个样本的预测值, y̅为n个样本预测值的均值。 式(11)中n为样本个数, p为波长点个数, S1λi为仪器1测量的第i个样本在波长点λ 处的数据, S2λi为仪器2测量的第i个样本在波长点λ 处的数据, 该公式先得到一个样本在所有波长点的绝对平均误差再累加所有样本取平均。 式(12)中ARMSuncorrected是未经过模型传递算法进行校正的光谱平均误差, ARMScorrected是经过模型传递算法进行校正的光谱平均误差。 本实验将采用这四个指标来评估TCADS算法与其他模型传递算法的效果。

2 结果与讨论
2.1 主机从机间光谱差异

玉米数据集以m5为主机, mp5和mp6为从机进行模型传递时, 主机与从机之间的光谱差异如图2(a)所示。 药品数据集以A1为主机, A2为从机进行模型传递时, 主机与从机之间的光谱差异如图2(b)所示。

图2 玉米(a)和药品(b)数据集上主机与从机的光谱差异Fig.2 Spectral differences between different instruments on corn (a) and tablets (b) datasets

2.2 玉米数据集实验结果及讨论

玉米数据集80个样本采用KS算法以4:1的比例进行划分, 得到64个校正集样本和16个测试集样本。 采用偏最小二乘法(partial least square, PLS)对主机训练集样本进行全谱建模, 经网格搜索交叉验证后得到主成分为9时模型效果较好, 因此主成分选择9进行模型训练。 训练后的模型对主仪器测试集样本进行预测, 水分的R2为 0.995 7, RMSEP为0.019 6; 油脂的R2为 0.874 5, RMSEP为0.064 2; 蛋白质的R2为 0.975 1, RMSEP为0.079 9; 淀粉的R2为0.907 8, RMSEP为0.214 5。 在主机m5上预测玉米四种成分效果较好, 将校正模型传递到从机mp5和从机mp6。 实验分别对比了直接预测, DS, PDS, SBC以及TCADS算法的模型传递效果并进行讨论。

表1为不采用任何传递方案, 主仪器的模型不能很好的适用于从仪器采集的数据, 预测均方误差较高, 预测效果较差; 而采用模型传递算法后显著降低了预测均方误差, 提高了预测精度。 使用TCADS 算法传递后, 两个从仪器的四种成分共计八个预测结果中, 六个预测结果为最优, 两个预测结果为次优。 计算八个结果的平均RMSEP, 得到四种传递算法中TCADS的平均RMSEP最低, 达到了0.152 5, 表明TCADS 算法相比于传统模型传递算法能进一步降低预测均方误差。 对比其他研究, Cui等[17]提出了一种相互-个体因子分析的模型传递算法(MIFA), 选取公开的玉米数据集进行实验, 通过PLS建立主机油脂含量预测模型, 并使用RMSEP作为模型预测评价指标。 将主机模型采用MIFA算法传递到从机mp5时, 将RMSEP从0.166 7降低到了0.143 5。 而本实验采用TCADS算法传递后, 主机模型预测mp5数据的RMSEP从0.163 1降低到了0.093 6, 进一步验证了TCADS算法的有效性。

表1 在玉米数据集上使用不同传递算法的预测均方误差(RMSEP) Table 1 RMSEPof different transfer algorithms forcorn dataset

以决定系数R2为指标采用TCADS算法进行传递时, 六个预测结果为最优, 两个预测结果为次优(见表2)。 DS算法虽整体表现较好且两个指标达到最优, 但在预测mp5仪器上的淀粉含量时, R2直接降低到了0.371 3。 出现这一情况的根本原因是线性校正算法的鲁棒性不够强, 存在不稳定性。 在预测该指标时可能由于光谱噪声等因素出现了过校正, 导致这一指标最终的结果与真实结果具有较大差异。 PDS虽相比于直接预测效果有提升, 但是相比于其他算法效果不够好。 SBC算法虽在 mp6机器上预测蛋白质含量时R2高达0.901 4, 但预测其他指标时结果不佳。 本研究提出的TCADS算法是较为稳定的一种模型传递算法, 平均R2为0.850 6, 相较于传统算法具有较好鲁棒性。

表2 在玉米数据集上使用不同传递算法的决定系数(R2) Table 2 R2 of different transfer algorithms for corn dataset

表3以预测蛋白质为例, 展示了玉米数据集上不同算法的ARMS和Prcorrected, 由于SBC是基于结果进行校正的算法而不是基于光谱校正的算法, 因此无法评估ARMS和Prcorrected这两个指标。 实验结果表明从机mp5采用TCADS算法将光谱平均差异从直接预测的0.213 5降低到了0.033 1, 光谱平均校正率达到了0.976 0。 从机mp6采用TCADS算法将光谱平均差异从直接预测的0.239 9降低到了0.048 1, 光谱平均校正率达到了0.959 8。 实验表明, 相比于其他传递算法, TCADS算法能将光谱之间差异降到最低, 模型传递效果最好。

表3 在玉米数据集上使用不同传递算法的平均光谱差异(ARMS)和平均光谱校正率(Prcorrected) Table 3 ARMS and Prcorrected of different transfer algorithms for corn dataset
2.3 药品数据集上的实验结果及讨论

药品数据集共有655个样本, 模型预测标签包括药品质量, 药品硬度以及药品活性成分。 由于药品质量和药品硬度这两个标签建模效果不佳, 因此选取活性成分作为预测标签进行建模与模型传递实验。 首先将药品数据集预先划分的训练集, 验证集和测试集进行合并便于后续重新划分。 由于药品数据集的原始光谱图后段谱峰重叠, 噪声较大, 因此舍弃波长后段120个波长点, 只采用前面530个波长点进行建模。 建模前先采用PLS算法进行留一交叉验证去除异常样本, 比较每一样本的预测值和真实值, 将均方误差大于30的样本标记为异常样本。 将19个异常样本去除后, 剩余的636个样本用KS算法以4:1划分为509个样本的校正集和127个样本的测试集。 使用PLS算法进行建模, 经网格搜索交叉验证后可得主成分为11时模型效果较好, 因此选择主成分为11进行模型训练。 训练后的模型对主机A1测试集样本进行预测, 样品活性成分含量R2为0.982 5, RESMP为1.938 4。 虽然该校正模型在主机A1采集的测试集光谱样本上表现效果较好, 但直接预测从机A2采集的测试集光谱样本却表现不佳, R2为0.684 5, RESMP为8.230 3。 因此需要进行模型传递, 以达到在模型能够同时在主机和从机上都有较好的预测性能。 实验分别对比了直接预测, DS, PDS, SBC以及TCADS算法的模型传递效果并进行讨论。

由表4发现, 在药品数据集上直接对从机样本进行预测时R2为0.684 5, 虽相比于预测主机光谱性能明显降低, 但模型不至于完全失效; 因此可知药品数据集仪器间光谱差异相对较小, 对不同仪器之间的差异敏感度较低。 实验表明四种模型传递算法中, 所提出的TCADS算法效果最好, 传递后预测从仪器药品活性成分时RMSEP从直接预测的8.230 3降低到了1.871 4, R2从直接预测的0.684 5提升到了0.983 7。 对比其他研究, Zhang等[18]同样在药品数据集上通过PLS建立主机模型, 并选取R2和RMSE作为模型传递算法的评价指标。 采用NS-PFCE算法将主机模型传递到从机, 分别使用了相关系数约束, L2范数约束和L1范数约束进行实验。 实验结果表明, 使用三种约束的NS-PFCE算法传递后, 分别将主机模型的RMSE降低到了3.28, 3.31和3.40, R2提升到了0.983, 0.983和0.982。 而所提出的TCADS算法传递后相比于NS-PFCE的R2稍有提升, RMSE降低较为显著, 再次证明了本算法的有效性。 图3为采用TCADS算法传递前后从机测试集样本的预测值-真实值相关图, 图中模型传递前散点偏离对角线, 多数样本预测值大于真实值, 少数样本预测值小于真实值。 说明即使在去除异常样本后, 主机模型直接预测从机样本时预测值与真实值仍有较大差距。 采用TCADS算法对主机模型进行传递后, 可以看到散点接近对角线并均匀分布在两侧, 表明经TCADS模型传递后主机模型预测从机样本时能取得较好的预测效果。

表4 在药品数据集上使用不同传递算法得到的决定系数(R2)和预测均方误差(RMSEP) Table 4 R2 and RMSEP of different transfer algorithms fortablets dataset

图3 TCADS算法使用前后预测值-真实值相关图
表5中TCADS模型传递算法的ARMS从直接预测的0.178 9降到了0.024 0, 优于DS算法的0.276 7和PDS算法的0.099 8。 TCADS模型传递算法的Prcorrected达到了0.982 0, 优于DS算法的-1.392 2和PDS的0.688 8。 药品数据集上由于仪器之间的差异相对较小, 因此DS算法出现了过校正, 校正后反而增大了光谱差异, 导致光谱校正率为负。 对比传统的模型传递算法, TCADS算法有效减缓了线性校正可能带来的过校正的问题, 能够将不同仪器间的光谱差异降到最低, 模型传递的效果最好。Fig.3 Correlograms of predicted and true values before and after the use of TCADS algorithm

表5 在药品数据集上使用不同传递算法得到的平均光谱差异(ARMS)和光谱校正率(Prcorrected) Table 5 ARMS and Prcorrected using different transfer algorithms on tablets dataset
3 结论

提出了一种将迁移学习与传统模型校正结合的模型传递新方法即TCADS算法。 TCADS将源域数据与目标域数据映射到一个高维的再生核希尔伯特空间, 在这个空间内主机光谱数据和从机光谱数据具有较小的最大均值差异。 映射后的数据在保留主要特征的同时分布具有较高的相似性, 在此基础上再次采用传统的DS算法进行二次校正, 改善了DS算法可能带来的过拟合问题, 进一步提高了模型传递效果。 根据在玉米数据集以及药品数据集两个公开数据集上的实验, 表明TCADS算法是一种高效且稳定的模型传递方案。 传统的模型传递算法在不同的数据集上模型传递的效果波动较大。 以R2指标为例, DS算法在玉米数据集上的传递效果整体不错, 但是在药品数据集上出现了过校正的问题, 传递效果不佳; PDS算法在药品数据集上可以达到0.955 6, 明显高于DS算法和SBC算法, 但在玉米数据集上校正结果很差, 甚至出现了R2为负的情况。 而本文提出的TCADS算法无论是在仪器间光谱差异较大的玉米数据集上(ARMS为0.213 5和0.239 9)还是在仪器间光谱差异相对较小的药品数据集上(ARMS为0.178 9), 都表现出了较好的模型传递效果。 实验表明TCADS 算法相比于传统的模型传递算法性能有所提升, 为模型传递问题提供了一种有效且稳定的解决方案。

参考文献
[1] Reda R, Saffaj T, Bouzida I, et al. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2023, 303: 123213. [本文引用:1]
[2] Díaz E O, Iino H, Koyama K, et al. Food Chemistry, 2023, 429: 136907. [本文引用:1]
[3] Ojala K, Myrskyranta M, Liimatainen A, et al. International Journal of Pharmaceutics, 2020, 577: 119028. [本文引用:1]
[4] Santos F D, Vianna S G T, Cunha P H P, et al. Microchemical Journal, 2022, 181: 107696. [本文引用:1]
[5] Mishra P, Roger J M, Rutledge D N, et al. Postharvest Biology and Technology, 2020, 170: 111326. [本文引用:1]
[6] Huang G, Chen X, Li L, et al. Chemometrics and Intelligent Laboratory Systems, 2020, 201: 103986. [本文引用:1]
[7] Li L, Huang W, Wang Z, et al. Postharvest Biology and Technology, 2022, 183: 111720. [本文引用:1]
[8] Wang Y, Veltkamp D J, Kowalski B R. Analytical Chemistry, 1991, 63(23): 2750. [本文引用:1]
[9] Tan H W, Brown S D. Journal of Chemometrics, 2001, 15(8): 647. [本文引用:1]
[10] Bouveresse E, Hartmann C, Massart D L, et al. Analytical Chemistry, 1996, 68(6): 982. [本文引用:1]
[11] Sun X D, Wu H L, Chen Y, et al. Chemometrics and Intelligent Laboratory Systems, 2019, 194: 103869. [本文引用:1]
[12] Munnaf M A, Mouazen A M. Soil and Tillage Research, 2023, 225: 105545. [本文引用:1]
[13] Qi Y, Liu Y, Luo J. PhotoniX 4, 22(2023). https://doi.org/10.1186/s43074-023-00098-0. [本文引用:1]
[14] LIU Cui-ling, ZHOU Zi-yan, LI Tian-rui, et al(刘翠玲, 周子彦, 李天瑞, 等). Journal of Food Science and Technology(食品科学技术学报), 2019, 37(4): 95. [本文引用:1]
[15] Pan S J, Tsang I W, Kwok J T, et al. IEEE Transactions on Neural Networks, 2010, 22(2): 199. [本文引用:1]
[16] Kennard R W, Stone L A. Technometrics, 1969, 11(1): 137. [本文引用:1]
[17] Cui X. Molecules, 2022, 27(18): 6069. [本文引用:1]
[18] Zhang J, Zhou X, Li B. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2023, 301: 122978. [本文引用:1]