XPS数据用于计算薄膜厚度时的处理方法

引用本文

刘涵, 陈萌. XPS数据用于计算薄膜厚度时的处理方法[J]. 光谱学与光谱分析, 2024,44(12): 3301-3305.
LIU Han, CHEN Meng. Methods of Processing XPS Data for Calculating Film Thickness[J]. Spectroscopy and Spectral Analysis, 2024,44(12): 3301-3305.
Doi:10.3964/j.issn.1000-0593(2024)12-3301-05 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

XPS数据用于计算薄膜厚度时的处理方法

刘涵, 陈萌^*

复旦大学材料科学系, 上海 200433

*通讯作者 e-mail: chenmeng@fudan.edu.cn

作者简介: 刘涵, 1999年生, 复旦大学材料科学系硕士研究生 e-mail: 21210300053@m.fudan.edu.cn

收稿日期: 2023-09-21 修回日期: 2024-04-16

基金: 国家重点研发计划项目(2017YFA0207301), 国家自然科学基金项目(21890751)资助

摘要

X射线光电子能谱(XPS)技术能够提供样品表面各化学状态的元素的峰位、峰强等信息。通过这些信息以及光电子信号表达式, 可以计算出薄膜厚度。介绍了三种光电子信号表达式的处理方法: 直接求解法, 基底-比值法和角度-比值法; 分析了其推导过程。研究结果表明三种处理方式具有不同的精确度和适用范围。直接求解法没有适用限制, 但精确度低; 基底-比值法适用范围较小, 仅适用于计算厚基底上的薄膜厚度, 要求薄膜和基底组成成分具有相近的有效衰减长度 λ, 而这种方法受到仪器项和碳污染项误差的影响最小, 具有最高的计算精确度; 角度-比值法的适用范围和计算精确度适中, 无需考虑基底层的限制条件, 但出射角 θ的变化幅度对计算精确度有较大影响。因此在使用XPS数据计算薄膜厚度时, 研究者可以综合考虑上述各因素。

关键词: X射线光电子能谱(XPS); 角分辨X射线光电子能谱(ARXPS); 薄膜厚度

中图分类号:O484.5 文献标志码:R

Methods of Processing XPS Data for Calculating Film Thickness

LIU Han, CHEN Meng^*

Department of Materials Science, Fudan University, Shanghai 200433, China

*Corresponding author

Abstract

The X-ray Photoelectron Spectroscopy (XPS) technique can provide information about the chemical states of various elements on the sample surface and the peak intensities and positions of their spectra. The thickness of thin films can be calculated by utilizing this information and the equation for photoelectron signals. This paper introduces three methods for handling the equation of photoelectron signals: direct solving method, substrate-ratio method, and angle-ratio method. Their derivation processes are analyzed, and the results indicate that these three methods have different accuracies and applicability ranges. The direct-solving method has the widest applicability but the lowest accuracy. The substrate-ratio method has the most limited applicability range, being able to calculate the thickness of thin films only on substrates of infinite thickness, and the effective attenuation length λ of the composition of film and substrate composition needs to be similar. However, it is least affected by instrumental and carbon contamination errors, thus having the highest calculation accuracy. The angle-ratio method has a moderate applicability range and calculation accuracy, and it can be used without considering the limitation of the substrate layer. However, the variation in the emission angle θ significantly affects the calculation accuracy. Researchers can consider the above factors comprehensively when calculating the thickness of thin films using XPS data.

Keyword: X-ray photoelectron spectroscopy (XPS); Angle resolved X-ray photoelectron spectroscopy (ARXPS); Film thickness

文章图片

引言

X射线光电子能谱(XPS)技术是一种采用X射线入射至样品表面约10 nm以内深度并激发出携带相关信息的光电子表面分析技术, 能提供不同化学环境下各元素的能谱峰强、峰位等信息, 从而对材料表面元素进行定性和定量分析。 20世纪60年代, Siegbahn等开始了对XPS的研究^[1], 在1974年的文章中详细介绍了当时XPS的成果与展望, 包括X射线单色器对能谱分辨率的提高、仪器构造、不同凝聚态样品的能谱分析、光电子发射原理以及化学位移的产生原因等, 此时的研究主要关注材料所含元素化学状态的定性分析^[2]。

随着XPS技术的发展, 发现XPS数据可以能够既便捷又相对准确地分析薄膜厚度。然而未经适当处理的XPS数据可能会导致分析结果出现较大的误差。 Fadley首先采用XPS技术定量分析了薄膜厚度, 提出了根据光电子强度关系式计算厚度的观点^[3], 进一步提出了基底-比值法的计算方法^[4]。 Seah等采用Si/SiO₂材料构建了两层结构模型, 并将碳污染具象化为薄膜纳入计算^{[5, 6, 7]}。在考虑碳污染的情况下给出了与Fadley相同的基底-比值法计算公式, 并提出了碳污染等误差的修正方法。有研究简要总结了基底-比值法, 包括计算公式, 相关常数的理论计算方法以及样品和数据的处理等^[8]。

XPS技术中光电子从样品表面逸出的深度与电子的动能有关, 角分辨X射线光电子能谱(ARXPS)通过调整入射X射线角度, 根据信号强度随角度的变化可计算出薄膜厚度, 即角度-比值法。 Aarnink在总结基底-比值法的基础上提到了采用角度信息计算膜厚的方法^[9]。本工作在具体介绍前述采用XPS数据计算膜厚的方法, 分析三种方法的计算过程, 使研究者在工作中可以准确选用数据处理的方法。

1 XPS仪器构造及信号激发过程

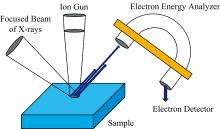
X射线光电子能谱仪发展至今已有非常精密复杂的结构, 简化后其主要功能器件如图1所示, 包含以下几个部分: X射线源、离子枪、样品台、能量分析仪以及检测器。

	Figure Option View Download New Window
	图1 XPS仪器构造Fig.1 Instrument construction of XPS

XPS的射线源通常是镁或铝作为阳极靶材得到的Mg Kα 和Al Kα 射线, 其光子能量分别为1 253.6和1 486.6 eV, 足以激发除H和He以外的元素。射线源产生的X射线被单色器单色和聚焦后照射样品表面, 样品中的电子受激发射并被能量分析器接收, 能量分析器内部采用静电场或者磁场筛选出对应动能的电子传入检测器, 经过光电倍增管等器件的信号调制和放大后, 最终获得电子能量分布。配备的离子枪可用于荷电中和、样品表面清洁和深度剖析实验。

光电子的出射过程理论上可能受到弹性碰撞和非弹性碰撞的影响。若认为光电子的出射过程只由非弹性碰撞贡献, 忽略弹性碰撞的影响, 研究者们将其称之为直线近似(SLA), 若考虑弹性碰撞对光电子的影响, 研究者们将其称之为有效衰减近似^[10](EAL)。

XPS基于SLA和EAL两种近似的信号激发过程如图2所示。

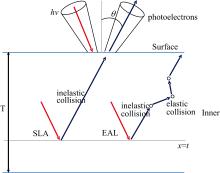	Figure Option View Download New Window
	图2 XPS基于SLA和EAL近似的信号激发过程Fig.2 Signal excitation process of XPS based on SLA approximation and EAL approximation

在距表面任意距离t处, Jablonski等给出了以非弹性碰撞模型的SLA近似为基础的XPS激发信号表达式^[10]

$\begin{array}{l} dI = S (E) Δ Ω FNA \frac{d σ}{d Ω} e^{- \frac{t}{λ_{in} \cos θ}} d t \\ = I_{0} e^{- \frac{t}{λ_{in} \cos θ}} d t \end{array}$ (1)

式(1)中, S(E)是仪器的检测器效率和分析器传输效率的函数, Δ Ω 是检测器的立体接受角, F是X射线的光子通量, N是材料的原子体密度, A是分析面积, $\frac{d σ}{d Ω}$ 是光电发射截面, 为描述方便, 前述参数合并为原始激发信号强度I₀, λ _in是光电子的非弹性平均自由程。指数项表征材料从激发至逸出表面的信号衰减程度, 满足Beer-Lambert方程对波的衰减描述形式, θ 为出射光电子与样品表面法线的夹角。

薄膜测量应用中的材料通常是均匀固体, 研究表明在均匀固体中, 其弹性碰撞对受激光电子的影响不可忽略^{[11, 12]}, 研究者们^{[13, 14]}用EAL近似略微修正了SLA近似, 开发了有效衰减长度L参数来替代非弹性平均自由程λ _in, 更好地表达了弹性碰撞在激发过程中的贡献。激发信号经替代和化简后用如式(2)表述

$dI = I_{0} e^{- \frac{t}{L \cos θ}} d t$ (2)

薄膜出射信号的总强度通过对不同深度处发射出的光电子进行积分得到, 见式(3)

$I = I_{0} \int_{0}^{T} e^{- \frac{t}{L \cos θ}} d t = I_{0} L \cos θ (1 - e^{- \frac{T}{L \cos θ}})$ (3)

2 XPS技术对表面薄膜厚度分析

2.1 结构模型

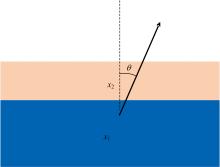
对于需要定量分析表面薄膜厚度的材料, 可以构造Seah等^[5]提到的分层模型进行分析(见图3), 以基底上单层薄膜的两层模型为例。

	Figure Option View Download New Window
	图3 两层模型信号激发示意图Fig.3 Schematic diagram of signal excitation of two-layer model

源于x₁层的受激光电子在穿越x₂层时信号进一步减弱, 各层的激发信号如式(4)和式(5)表述

$I_{x_{1}} = I_{0, x_{1}} L_{x_{1}, x_{1}} \cos θ (1 - e^{(- \frac{T_{x_{1}}}{L_{x_{1}, x_{1}} \cos θ})}) e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ})}$ (4)

$\begin{array}{l} I_{x_{2}} = I_{0, x_{2}} L_{x_{2}, x_{2}} \cos θ (1 - e^{(- \frac{T_{x_{2}}}{L_{x_{2}, x_{2}} \cos θ})}) \end{array}$ (5)

式(4)和式(5)中, $I_{x_{i}}$ 表示i层材料的出射信号强度; $L_{x_{i}, x_{j}}$ 表示i层材料元素的激发光电子在j层中的有效衰减长度; $T_{x_{i}}$ 表示i层材料的取样深度, 对于量程范围内的薄膜, 就是它自身的厚度。

2.2 直接求解

表达式(5)中I₀、 L及cosθ 三项均为常数, 若已知其的值则可以直接求解等式计算薄膜x₂层的厚度, 但通常会有较大的计算误差。为分析误差来源, 将式(3)中出射信号的总强度I还原为各物理参数表示, 仪器项和材料自身性质项分别用中括弧分离可得式(6)

$I = [S (E) Δ Ω FAcos θ] [N \frac{d σ}{d Ω} L] (1 - e^{- \frac{T}{L \cos θ}})$ (6)

第一个误差来源于常数项(包含仪器项和材料自身性质项), 常数项目前尚不能通过理论计算获得精确数值, 因此使用理论值将会带来一定的误差。若常数项数值通过单一批次样品的数据拟合获得, 可以一定程度上减小其带来的误差, ARXPS的激发信号与常规XPS无异, 直接求解的方式所导致的误差与常规XPS相同, 其常数项可以通过实测数据拟合确定^[15]。若考虑不同批次、仪器或者组成变化的材料测试, 反复使用某一次拟合的计算值, 仍难以避免误差。若每次测量都重新拟合常数, 则将导致计算过程繁琐且难以测量少量样品, 需要一定数量的样品相互校正以拟合常数。

另一个误差来源于碳污染项, 两层模型未考虑碳污染项的影响, 而碳污染是普遍存在于薄膜表面, 若将其直接忽略将带来不小的误差。例如, Smith^[16]等发现碳污染层厚度的错误估计将对数据带来约百分之三的影响, 通过后修正的方式, 进行了碳污染的校正工作, 最终将计算结果的平均误差从8.2%减小到5.6%。

2.3 基底-比值法

基底-比值法是一种更精确计算薄膜厚度的方法。减小了仪器项的误差, 并将碳污染项纳入考虑, 进行了合理的近似。采用Seah等提到的方法, 可以将碳污染具象为有一定厚度的薄膜, 相似的构建带碳污染层的两层模型, 如图4所示。

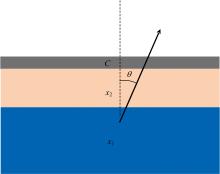	Figure Option View Download New Window
	图4 含碳污染的两层模型信号激发示意图对于含碳污染的模型, 有如式(7)— 式(9)光电子信号表达式Fig.4 Schematic diagram of signal excitation of two-layer model with considering of carbon contamination

$\begin{array}{l} I_{x_{1}} = I_{0, x_{1}} L_{x_{1}, x_{1}} \cos θ [1 - e^{(- \frac{T_{x_{1}}}{L_{x_{1}, x_{1}} \cos θ})}] \cdot \\ e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ})} e^{(- \frac{T_{C}}{L_{x_{1}, C} \cos θ})} \end{array}$ (7)

$I_{x_{2}} = I_{0, x_{2}} L_{x_{2}, x_{2}} \cos θ [1 - e^{(- \frac{T_{x_{2}}}{L_{x_{2}, x_{2}} \cos θ})}] e^{(- \frac{T_{C}}{L_{x_{2}, C} \cos θ})}$ (8)

$I_{C} = I_{0, x_{c}} L_{x_{c}, x_{c}} \cos θ e^{(- \frac{T_{C}}{L_{C, C} \cos θ})}$ (9)

等式相比可消除仪器项的误差, 碳污染表达式因信号弱且吸附膜不均匀不用于计算。 x₁层和x₂层的信号表达式在相比时存在多余未知数 $T_{x_{1}}$ , 因此假设基底层x₁厚度远大于其光电子有效衰减长度, 可将式(7)转变为式(10)

$I_{x_{1}} = I_{0, x_{1}} L_{x_{1}, x_{1}} \cos θ e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ})} e^{(- \frac{T_{C}}{L_{x_{1}, C} \cos θ})}$ (10)

式(8)和式(10)等光电子信号表达式中的常数可以通过拟合或者对应组分的无限厚固体模型的实测数据确定。将式(3)的采样深度扩展至无限厚, 可以采用如式(11)表述

$I_{x}^{\infty} = I_{0} L \cos θ (1 - e^{- \frac{x_{\infty}}{L \cos θ}})$ (11)

式(11)替换式(8)和式(10)后, 两者相比化简可以得到式(12)

$\frac{I_{x_{2}}}{I_{x_{1}}} \frac{I_{x_{1}}^{\infty}}{I_{x_{2}}^{\infty}} = \frac{1 - e^{(- \frac{T_{x_{2}}}{L_{x_{2}, x_{2}} \cos θ})}}{e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ})}} \frac{e^{(- \frac{T_{C}}{L_{x_{2}, C} \cos θ})}}{e^{(- \frac{T_{C}}{L_{x_{1}, C} \cos θ})}}$ (12)

对于比值法, 在任意实验中, 测试过程中光电子信号强度I包含的仪器项被相比消去。表明对于某种组成确定的材料, 拟合能获得一个稳定精确的经验常数K= $\frac{I_{x_{1}}^{\infty}}{I_{x_{2}}^{\infty}}$ 。

等式相比可减小处理碳污染时的误差, 分析方程中含未知数T_C一项, 见式(13)

$\frac{e^{(- \frac{T_{C}}{L_{x_{2}, C} \cos θ})}}{e^{(- \frac{T_{C}}{L_{x_{1}, C} \cos θ})}} = e^{[- \frac{T_{C}}{\cos θ} (\frac{1}{L_{x_{2}, C}} - \frac{1}{L_{x_{1}, C}}]}$ (13)

Seah等^[14]指出在0< θ < 58° , 6< Z< 83时, 参数L可通过如式(14)估计

$L / λ = 0.979 \times [1 - ω (0.955 - 0.077 7 \ln Z)]$ (14)

式(14)中, ω =λ /(λ +λ _tr), λ 是光电子的非弹性平均自由程, λ _tr是迁移平均自由程, θ 为出射电子与样品表面法线的夹角, Z为原子序数, 对于化合物采用平均值。式(14)中λ 可以通过Tanuma等^{[17, 18]}的工作计算取值。采用式(14)即可以估算x₁层和x₂层在碳污染层中有效衰减长度 $L_{x_{1}, C}$ 和 $L_{x_{2}, C}$ , 当基底x₁层和薄膜x₂层的平均原子序数差距不大时, $L_{x_{1}, C}$ ≈ $L_{x_{2}, C}$ 。同时, 由于碳污染层极薄, 而材料的有效衰减长度L和cosθ 是有限的常数, 可以进行近似

$e^{[- \frac{T_{C}}{\cos θ} (\frac{1}{L_{x_{2}, C}} - \frac{1}{L_{x_{1}, C}})]} \approx 1$ (15)

将式(15)与式(10)中碳污染项进行比较。注意到当 $L_{x_{1}, C}$ ≈ $L_{x_{2}, C}$ 时, 式(15)中的有效衰减长度项是式(10)的高阶无穷小, 采用指数函数的一阶泰勒展开式进行评估

$\begin{array}{l} e^{(- \frac{T_{C}}{L_{x_{1}, C} \cos θ})} = 1 - \frac{1}{L_{x_{1}, C}} \frac{T_{C}}{\cos θ} + o (- \frac{T_{C}}{L_{x_{1}, C} \cos θ}) \\ e^{[- \frac{T_{C}}{\cos θ} (\frac{1}{L_{x_{2}, C}} - \frac{1}{L_{x_{1}, C}})]} = 1 - o (\frac{1}{L_{x_{1}, C}}) \frac{T_{C}}{\cos θ} + \end{array}$ (16)

$o (- o (\frac{1}{L_{x_{1}, C}}) \frac{T_{C}}{\cos θ})$ (17)

式(16)和式(17)表明在对碳污染的处理中, 比值法的近似更合理, 这一点在Mitchell等的工作中已通过实验数据证明^[19]。若 $L_{x_{1}, x_{2}}$ 和 $L_{x_{2}, x_{2}}$ 根据式(14)估算数值也可以进行相同的近似, 则进一步化简后可得

$T_{x_{2}} = L_{x_{1}, x_{2}} \cos θ \ln (1 + K \frac{I_{x_{2}}}{I_{x_{1}}})$ (18)

式(18)中, $K = \frac{I_{x_{1}}^{\infty}}{I_{x_{2}}^{\infty}}$ , 可以通过测量无限厚固体或多组实测数据拟合计算获得, $I_{x_{1}}$ 和 $I_{x_{2}}$ 通过实验所测峰面积获得。基底-比值法同时减小了仪器误差和碳污染误差, 此方法对于XPS和ARXPS均适用。 Seah等^[7]在Si基底的SiO₂薄膜样品中采用式(18)对表面层SiO₂实测数据进行计算, XPS的膜厚计算结果与诸如: NRA、 RBS、 TEM等测试结果相近且具有良好的线性关系, 表明式(18)用于计算具有可行性。

2.4 角度-比值法

与常规XPS不同, ARXPS从不同的角度采集样品信息, 谱峰的强度会随X射线入射角的变化产生相应的改变, 因此ARXPS可以特别利用此关系作角度-比值法(见图5)。

	Figure Option View Download New Window
	图5 含碳污染的两层模型的ARXPS信号激发示意图在不同测试角度下有如式(19)和式(20)信号表达式Fig.5 Schematic diagram of ARXPS signal excitation of a two-layer model with considering of carbon contamination

$I_{x_{1}}^{1} = I_{x_{1}}^{\infty} e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ_{1}})} e^{(- \frac{T_{C_{1}}}{L_{x_{1}, C} \cos θ_{1}})}$ (19)

$\begin{array}{l} I_{x_{1}}^{2} = I_{x_{1}}^{\infty} e^{(- \frac{T_{x_{2}}}{L_{x_{1}, x_{2}} \cos θ_{2}})} e^{(- \frac{T_{C_{2}}}{L_{x_{1}, C} \cos θ_{2}})} \end{array}$ (20)

当假设碳污染项可通过相比直接去掉时, 式(19)/式(20)式可得式(21)

$T_{x_{2}} = \frac{L_{x_{1}, x_{2}} (\ln I_{x_{1}}^{1} - \ln I_{x_{1}}^{2})}{(\frac{1}{\cos θ_{1}} - \frac{1}{\cos θ_{2}})}$ (21)

采用两组不同测试角度的数据可计算膜厚, 而在实际计算时, 若选取的角度不同, 计算结果会出现不小的差距^[20], 被认为是碳污染项的处理方式带来的误差。当角度发生改变时, 碳污染层的实际有效厚度T_C将存在显著差别, 用 $T_{C_{1}}$ 和 $T_{C_{2}}$ 予以区分, 不能通过相比直接消去。因此相比直接求解, 角度-比值法由于等式相比的性质减小了仪器项的误差, 但相比于基底-比值法在碳污染项处理上仍存在不足。若角度差距很小时, 可以获得较好的数据, 且无需受基底层的限制。

3 结论

XPS技术在分析薄膜材料厚度中扮演了重要角色, 介绍了三种主要的XPS数据处理方法, 用于计算薄膜厚度。采用XPS和ARXPS技术获取的相关数据计算薄膜厚度时, 都可以采用直接求解法和基底-比值法, ARXPS还可以采用角度-比值法。通过分析其他研究者的推导过程和数据, 认为直接求解适用范围最广, 但不足以精确求解薄膜厚度。基底-比值法有效减小了仪器项误差和碳污染项误差的影响, 是三种方法中精确度最高的处理方法。这种方法的准确性依赖于两个关键的近似: 基底层厚度 $T_{x_{1}}$ 远大于其光电子的有效衰减长度L; 材料中相关元素有效衰减长度L的计算结果相近。这些近似决定了该方法的适用范围。角度-比值法在多次测量的角度偏差较大时, 对碳污染项的处理效果变差, 精确度变低, 但可适用于不考虑基底层的情况。

参考文献

文献列表

[1]	Siegbahn K, Nordling C, Fahlman A, et al. Annales De Physique, 1968, 3(5): 281. [本文引用:1]
[2]	Siegbahn K. Journal of Electron Spectroscopy and Related Phenomena, 1974, 5(11): 3. [本文引用:1]
[3]	Fadley C S. Journal of Electron Spectroscopy and Related Phenomena, 1974, 5(11): 725. [本文引用:1]
[4]	Fadley C S. Progress In Surface Science, 1984, 16(3): 275. [本文引用:1]
[5]	Seah M P, Spencer S J. Surface And Interface Analysis, 2002, 33(8): 640. [本文引用:2]
[6]	Seah M P. Surface And Interface Analysis, 2005, 37(3): 300. [本文引用:1]
[7]	Seah M P, Spencer S J, Bensebaa F, et al. Surface And Interface Analysis, 2004, 36(9): 1269. [本文引用:2]
[8]	LIU Fen, QIU Li-mei, ZHAO Liang-zhong, et al(刘芬, 邱丽美, 赵良仲, 等). Chemistry(化学通报), 2006, (5): 393. [本文引用:1]
[9]	Aarnink W, Weishaupt A, Vansilfhout A. Applied Surface Science, 1990, 45(1): 37. [本文引用:1]
[10]	Jablonski A. Computer Physics Communications, 2022, 272: 108233. [本文引用:2]
[11]	Jablonski A. Surface Science, 1996, 364(3): 380. [本文引用:1]
[12]	Jablonski A, Powell C J. Surface Science, 2012, 606(5-6): 644. [本文引用:1]
[13]	Jablonski A, Powell C J. Journal of Vacuum Science & Technology A, 2009, 27(2): 253. [本文引用:1]
[14]	Seah M P, Gilmore I S. Surface And Interface Analysis, 2001, 31(9): 835. [本文引用:2]
[15]	YAN Shao-ping, WANG Gui-hua, LI Feng, et al(严少平, 汪贵华, 李锋, 等). Journal of Hefei University of Technology(合肥工业大学学报), 2003, (3): 452. [本文引用:1]
[16]	Smith G C. Journal of Electron Spectroscopy and Related Phenomena, 2005, 148(1): 21. [本文引用:1]
[17]	Tanuma S, Powell C J, Penn D R. Surface and Interface Analysis, 1991, 17(13): 911. [本文引用:1]
[18]	Tanuma S, Powell C J, Penn D R. Surface And Interface Analysis, 1991, 17(13): 927. [本文引用:1]
[19]	Mitchell D F, Clark K B, Bardwell J A, et al. Surface And Interface Analysis, 1994, 21(1): 44. [本文引用:1]
[20]	PANG Zhong-jun, BAI Ming-wu, YAN Jie, et al(庞重军, 白明武, 严洁, 等). Journal of Materials Science and Engineering(材料科学与工程学报), 2007, 107(3): 349. [本文引用:1]

1968

0.0

... 20世纪60年代, Siegbahn等开始了对XPS的研究^[1], 在1974年的文章中详细介绍了当时XPS的成果与展望, 包括X射线单色器对能谱分辨率的提高、仪器构造、不同凝聚态样品的能谱分析、光电子发射原理以及化学位移的产生原因等, 此时的研究主要关注材料所含元素化学状态的定性分析^[2] ...

1974

0.0

1974

0.0

... Fadley首先采用XPS技术定量分析了薄膜厚度, 提出了根据光电子强度关系式计算厚度的观点^[3], 进一步提出了基底-比值法的计算方法^[4] ...

1984

0.0

... Fadley首先采用XPS技术定量分析了薄膜厚度, 提出了根据光电子强度关系式计算厚度的观点^[3], 进一步提出了基底-比值法的计算方法^[4] ...

2002

0.0

... Seah等采用Si/SiO₂材料构建了两层结构模型, 并将碳污染具象化为薄膜纳入计算^[5,6,7] ...

... 1 结构模型对于需要定量分析表面薄膜厚度的材料, 可以构造Seah等^[5]提到的分层模型进行分析(见图3), 以基底上单层薄膜的两层模型为例 ...

2005

0.0

... Seah等采用Si/SiO₂材料构建了两层结构模型, 并将碳污染具象化为薄膜纳入计算^[5,6,7] ...

2004

0.0

... Seah等采用Si/SiO₂材料构建了两层结构模型, 并将碳污染具象化为薄膜纳入计算^[5,6,7] ...

... Seah等^[7]在Si基底的SiO₂薄膜样品中采用式(18)对表面层SiO₂实测数据进行计算, XPS的膜厚计算结果与诸如: NRA、 RBS、 TEM等测试结果相近且具有良好的线性关系, 表明式(18)用于计算具有可行性 ...

2006

0.0

... 有研究简要总结了基底-比值法, 包括计算公式, 相关常数的理论计算方法以及样品和数据的处理等^[8] ...

1990

0.0

... Aarnink在总结基底-比值法的基础上提到了采用角度信息计算膜厚的方法^[9] ...

2022

0.0

... 若认为光电子的出射过程只由非弹性碰撞贡献, 忽略弹性碰撞的影响, 研究者们将其称之为直线近似(SLA), 若考虑弹性碰撞对光电子的影响, 研究者们将其称之为有效衰减近似^[10](EAL) ...

... 在距表面任意距离t处, Jablonski等给出了以非弹性碰撞模型的SLA近似为基础的XPS激发信号表达式^[10] ...

1996

0.0

... 薄膜测量应用中的材料通常是均匀固体, 研究表明在均匀固体中, 其弹性碰撞对受激光电子的影响不可忽略^[11,12], 研究者们^[13,14]用EAL近似略微修正了SLA近似, 开发了有效衰减长度L参数来替代非弹性平均自由程#cod#x003bb ...

2012

0.0

2009

0.0

2001

0.0

... Seah等^[14]指出在0#cod#x0003C ...

2003

0.0

... 若常数项数值通过单一批次样品的数据拟合获得, 可以一定程度上减小其带来的误差, ARXPS的激发信号与常规XPS无异, 直接求解的方式所导致的误差与常规XPS相同, 其常数项可以通过实测数据拟合确定^[15] ...

2005

0.0

... 例如, Smith^[16]等发现碳污染层厚度的错误估计将对数据带来约百分之三的影响, 通过后修正的方式, 进行了碳污染的校正工作, 最终将计算结果的平均误差从8 ...

1991

0.0

... 可以通过Tanuma等^[17,18]的工作计算取值 ...

1991

0.0

... 可以通过Tanuma等^[17,18]的工作计算取值 ...

1994

0.0

... 式(16)和式(17)表明在对碳污染的处理中, 比值法的近似更合理, 这一点在Mitchell等的工作中已通过实验数据证明^[19] ...

2007

0.0

... 采用两组不同测试角度的数据可计算膜厚, 而在实际计算时, 若选取的角度不同, 计算结果会出现不小的差距^[20], 被认为是碳污染项的处理方式带来的误差 ...