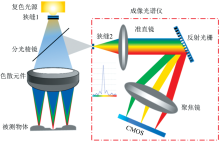
图1为线扫式光谱共焦原理示意图。 它主要由复色光源、 色散物镜和成像光谱仪三部分组成。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 光谱共焦原理示意图Fig.1 Schematic diagram of spectral confocal

光源能提供稳定的高亮度的复色光, 该系统波段范围是500~650 nm, 带宽是150 nm, 设计中心波长为550 nm。 色散物镜和分光棱镜一起决定了系统的轴向测量范围。 经被测表面反射的光线经过分光棱镜进入到成像光谱仪。 成像光谱仪主要由狭缝、 准直镜、 反射光栅、 聚焦镜和探测器组成。

复色光源发出的光经过狭缝和分光棱镜进入色散物镜, 由于不同波长的光在同一介质中的折射率不同, 通过色散物镜后不同波长的光会聚焦在光轴上不同位置, 即轴向色散。 当被测目标位于色散范围内时, 聚焦到被测表面的光线再次穿过色散物镜和分光棱镜进入到共焦狭缝, 没有聚焦到被测物体表面上的光线不能通过共焦狭缝, 从共焦狭缝发出的光线经过准直镜到达反射光栅, 再经聚焦镜的聚焦到CMOS探测器像面。 然后提取谱段的峰值波长, 通过建立波长和位移量之间的关系, 进而获得被测表面的深度信息。 从原理来看, 色散物镜是整个线扫式光谱共焦位移传感技术的核心, 系统的测量范围和扫描线长都受色散物镜光学结构的影响。 系统色散方向的分辨率则由成像光谱仪和色散物镜共同决定。 表1为高精度线扫式光谱共焦位移传感器的设计目标。

表1

Table 1

表1(Table 1)

表1 高精度线扫式光谱共焦位移传感器设计目标 Table 1 Design goal of high-precision line-scanning spectral confocal displacement sensor 设计指标 目标数值 扫描线长/mm ≥ 10 测量范围/mm ≥ 3 弥散斑半径/μ m ≤ 5.5 轴向分辨率/μ m ≤ 0.8

表1 高精度线扫式光谱共焦位移传感器设计目标 Table 1 Design goal of high-precision line-scanning spectral confocal displacement sensor

线扫式光谱共焦位移传感技术的设计难点:

(1) 相对于点扫式引入了扫描线长, 在色散物镜的光学设计中轴外像差激增, 给设计增加很大的难度。

(2) 线扫式光谱共焦位移传感器的色散物镜设计需要双远心光路, 物方需要保证绝对远心, 这样可以保证进入光谱仪中的光能量均匀, 像方远心则要求没有那么高, 在1° 以内即可, 可以消除不同波长放大倍率不同带来的影响。

(3) 目前对色散物镜的研究较多, 针对色散物镜后端的成像光谱仪研究很少, 往往采用商业化的产品; 要实现高精度的测量, 对成像光谱仪的光谱分辨率要求很高。

线扫式光谱共焦位移传感技术的测量范围主要由色散物镜决定。 色散物镜的设计要求为: 在保证扫描线长达到设计指标的情况下, 减少透镜片数, 缩短距离, 尽量减小各个视场的弥散斑半径, 并保证色散范围达到设计要求。

色散物镜的设计指标分为色散特性指标和光学设计指标。 根据上述高精度线扫式光谱共焦位移传感器的设计目标, 对色散物镜的色散特性参数进行指标分配; 如表2所示。

表2

Table 2

表2(Table 2)

表2 色散物镜色散特性参数指标 Table 2 Parameters of dispersive objective lens 设计指标 目标数值 扫描线长/mm ≥ 10 测量范围/mm ≥ 3 弥散斑半径/μ m ≤ 5.5

表2 色散物镜色散特性参数指标 Table 2 Parameters of dispersive objective lens

色散物镜设计与一般光学设计不同的是不仅不校正轴向色差, 而且还要增大轴向色差, 并且尽量保证线性色散。 轴向色差一般用F光和C光成像位置的差表示

Δl'FC=l'F-l'C(1)

式(1)中, l'_F和l'_C分别表示用F光和C光的折射率计算近轴光路所得到的近轴像距。 色散物镜的波段范围为λ ₀-λ ₁, 则色散物镜对应的轴向色差Δ l'_FC为

Δl'=l'λ0-lλ1(2)

线性轴向色差的理论公式如式(3)^[16]所示

φ=∑iNφdi∑i=1Nφi(λd)νdi(Pλi-Qλ)=0(3)

色散物镜的光学设计指标包括: 物方孔径, 工作距离, 放大倍率, 双远心光路远心度, 物方视场等参数。 经过上述色散物镜的理论分析, 针对线扫式光谱共焦位移传感器技术的设计难点, 提出了一种适合线扫式色散物镜的光学设计方法:

(1) 根据上述式(3)对初始结构的玻璃材料进行选择; 初始结构的选择有两种方法, 一种是运用近轴光学知识来计算初始结构参数, 再逐步调整达到设计目标, 但该方法对设计人员要求较高, 仅仅靠设计人员计算难以得出一个好的初始结构。 另一种是在已公开的文献或者专利中挑选一个合适的初始结构, 对所挑选结构进行优化设计。 初始结构挑选的原则是F数和视场角与设计指标匹配, 焦距可以通过软件缩放或者增大。 单片折射透镜不能获得线性色散, 因此需要多片透镜按照光学原理组合。 选择初始结构为双高斯结构, 以该结构作为起点开始设计。 该结构完全对称, 垂轴像差自动抵消, 简化了像差矫正过程。

(2) 色散物镜的色散范围主要由轴向色差来决定, 选择初始结构后, 在zemax设置多重结构来优化轴向色散。 首先, 以透镜材料为变量将轴向色散进行初步优化, 然后增加透镜半径和间隔以及厚度为变量, 根据设计指标添加操作数来控制色散范围、 像差、 放大倍率等因素。 在多重结构中设置一系列的波长, 使用AXCL操作数控制轴向色差及其线性度。

(3) 像差校正的方法: 除了轴向色差之外, 像差校正也是色散物镜设计需要重点注意的, 线扫式光谱共焦位移传感技术相对于点扫式引入了扫描线长, 也就是轴外像差, 轴外像差会随着视场的变大以幂函数的方式激增, 这也是线扫式光谱共焦位移传感技术的难点之一, 需要校正像差主要包括: 轴上点球差, 轴外像差, 以及色差。

像差矫正的方法有以下两种: (1) 对像差变化较大的玻璃, 采用玻璃替换的方式。 (2) 对相对孔径h/r或入射角很大的面使其弯向光, 以减小轴外像差。

根据上述理论分析, 使用光学设计软件zemax进行色散物镜的设计, 工作波段为500~650 nm, 选择的探测器像元大小为5.5 μ m。 最终的优化光学结构如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 色散物镜的优化后的结构图Fig.2 Optimized structure of dispersive objective lens

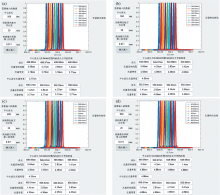
光学系统的点列图代表光学系统能量集中度。 如图3所示为优化后色散物镜的点列图, 由图3可知色散物镜各个波长的像差都得到了很好的校正且RMS直径均小于5.5 μ m。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 点列图 (a): 500 nm点列图; (b): 550 nm点列图; (c): 600 nm点列图; (d): 650 nm点列图Fig.3 Spot diagram (a): 500 nm spot diagram; (b): 550 nm spot diagram; (c): 600 nm spot diagram; (d): 650 nm spot diagram

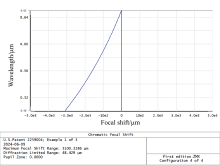
色焦移曲线就是用于确定光学系统轴向色差和波长的函数关系, 因此色焦移的大小可以作为评价色散范围大小的指标。 图4所示为色散物镜的色焦移图, 色焦移大于3 mm, 线性度拟合判定系数R²为0.992 1。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 色焦移图Fig.4 Color focal shift

最终色散物镜色散特性参数设计结果为: 扫描线长为10.2 mm, 色散范围为3.1 mm, 各个波长的弥散斑直径均小于5.5 μ m。 光学设计参数结果为: 物方孔径0.1, 工作距离为56.87~60 mm, 放大倍率为0.85, 物方绝对远心, 像方远心在1° 以内, 物方视场为12 mm。 色散物镜色散特性参数设计结果均达到上述设计目标要求。

成像光谱仪可以获得待检测目标的单色光谱像, 并将空间维信息和光谱信息结合成三维待测目标立方体数据, 从而为研究人员提供了探测目标空间维以及光谱维的特征细节^[17], 目前已经在各个领域广泛应用^{[18, 19, 20]}。 光谱仪一般都有准直镜, 分光元件, 聚焦镜和探测器组成。 采取准直镜和聚焦镜为完全对称的结构, 这样可以抵消部分像差, 简化光学设计过程。 常用的分光元件有光栅和棱镜。 棱镜分光与材料折射率和顶角角度有关^[21], 棱镜材料对不同的波长有不同的折射率, 在棱镜的楔角α 确定的情况下, 一束光的出射偏向角θ 与入射角i的关系可以表示为

θ=i+arctannsinα-arctansinin-α(4)

当入射角不变时, 偏向角是折射率n的函数, 所以不同波长的偏向角会不同, 从而将不同波长的光分开。 棱镜分光的缺点是棱镜色散非均一且色散率低。

相对棱镜而言, 光栅的光谱分辨率高, 光谱范围宽且色散均一。 光栅又分为透射光栅和反射光栅, 透射光栅受限于光栅制作材料的透射光谱特性, 使用时光谱范围受到限制, 且光能利用率较低, 因此选择反射光栅作为分光元件。

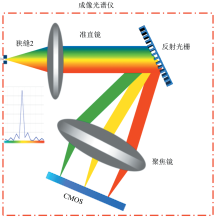
该系统的结构原理图如图5所示, 分光元件首先通过准直镜使狭缝发出的光准直射入到光栅上, 光栅负责将该波段的波长在色散方向上分开, 经聚焦镜成像在探测器接收面。 探测器部分负责接收和显示该波段的光谱信息。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 成像光谱仪原理图Fig.5 Schematic diagram of imaging spectrometer

成像光谱仪的光谱分辨率由系统的设计指标决定, 若该光谱共焦线扫式测量系统的位移分辨率为δ L, 工作的波段范围使Δ λ , 系统的测量范围使Δ L, 则该成像光谱仪需要达到的光谱分辨率为

δλ=Δλ×δLΔL(5)

测量范围设计目标为3 mm, 工作波段为500~650 nm, 位移分辨率为0.8 μ m, 代入式(5)可得该成像光谱仪需要的光谱分辨率至少为0.04 nm。

成像光谱仪工作波段要包含色散物镜的工作波段, 所以设计其工作波段为490~660 nm, 中心波长为575 nm。 光谱分辨率主要由准直镜和聚焦镜的焦距和孔径决定。 准直镜的焦距f₁与分辨率之间满足

Δλ=acosinf1(6)

式(6)中, a为狭缝宽度, n为光栅刻线密度。

聚焦镜的焦距f₂应满足

f2=hcosθcosγn(λ1-λ2)(7)

式(7)中, γ 为探测器与垂直方向的夹角, h为探测器像面长度, n为光栅刻线密度。

目前在可见光波段常用的光栅刻线数为1 200和600线· mm^-1。 根据所需光谱分辨率以及整体结构布局, 确定光栅参数如表3所示。

表3

Table 3

表3(Table 3)

表3 成像光谱仪设计参数 Table 3 Parameters of the imaging spectrometer 组件名称 参数 数值 准直镜 焦距 230 mm 聚焦镜 焦距 230 mm 光栅 光栅刻线数 1 200线· mm-1 狭缝尺寸 长度× 宽度 12 mm× 11 μ m 像元大小 尺寸 5.5 μ m× 5.5 μ m

表3 成像光谱仪设计参数 Table 3 Parameters of the imaging spectrometer

上面阐述了光栅光谱仪的一些基本原理以及各部件的设计, 按照上述参数设置成像光谱仪并在软件中对光路进行优化设计。 优化结果如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 成像光谱仪结构优化结果Fig.6 Optimized structure of imaging spectrometer

成像光谱仪的成像质量评价仍然选用点列图作为评价标准, 要求弥散斑直径一个像元大小, 如图7为四个采样波段500、 550、 600和650 nm的点列图情况。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 点列图 (a): 500 nm点列图; (b): 550 nm点列图; (c): 600 nm点列图; (d): 650 nm点列图Fig.7 Spot diagram (a): 500 nm spot diagram; (b): 550 nm spot diagram; (c): 600 nm spot diagram; (d): 650 nm spot diagram

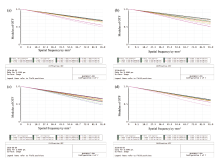
光学传递函数, 即MTF曲线, 是反映不同物体不同频率成分传递能力。 MTF曲线是评价光学成像系统的最系统的方法。 本成像光谱仪选用的探测器像元大小为5.5 μ m, 对应的奈奎斯特截止频率为=1/(5.5(μ m)× 2)=91 lp· mm^-1, 图8所示为中心波长处MTF调制函数曲线, 可以看出在截止频率处仍大于0.5, 接近衍射极限, 满足成像质量要求。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 光学传递函数MTF图 (a): 500 nm处MTF曲线; (b): 550 nm处MTF曲线; (c); 600 nm处MTF曲线; (d): 650 nm处MTF曲线Fig.8 MTF diagram of optical transfer function (a): MTF curve at 500 nm; (b): MTF curve at 550 nm; (c): MTF curve at 600 nm; (d): MTF curve at 600 nm

zemax无法读出光谱仪分辨率确切数值, 需要根据光谱仪分辨率的理论公式从zemax软件中读取所需要的数据, 再使用matlab软件进行仿真, 才能得到光谱仪分辨率的数值大小, 理论公式^[22]如式(8)

SFR(y)=rectya×LSFT(y)×rectya(8)

式(8)中, x代表卷积, a代表狭缝宽度, 两个矩形函数分别对应狭缝函数和探测器函数, y代表了像面坐标。 LSF(y)代表了位置处的线扩散函数, 通过相同y坐标的点扩散函数对狭缝长度方向积分获得。 通过编写宏语言指令, 从zemax软件中读取点扩散函数, 不同波长在像面的位置等数据, 通过matlab仿真得到光谱分辨率结果, 如图9所示, 可以看出在距离四个中心波长0.04 nm带宽的波长分开的距离均在一个像元的大小, 说明该成像光谱仪的分辨率达到0.04 nm。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 光谱仪分辨率仿真图 (a): 500 nm处光谱响应函数曲线; (b): 550 nm处光谱响应函数曲线; (c): 600 nm处光谱响应函数曲线; (d): 650 nm处光谱响应函数曲线Fig.9 Spectrometer resolution simulation (a): Spectral response function curve at 500 nm; (b): Spectral response function curve at 550 nm; (c): Spectral response function curve at 600 nm; (d): Spectral response function curve at 650 nm

整个系统是由色散物镜与成像光谱仪两部分组合而成, 中间的分束棱镜会使从被测物表面返回来的光线进入成像光谱仪。 成像光谱仪再将入射光经过准直, 分光后再经聚焦镜会聚到探测器接受面上, 光谱共焦线扫式位移测量系统整体光路图如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 光谱共焦线扫式测量全系统结构图Fig.10 Line-scanning confocal spectral meaurement system

根据该系统原理分析, 聚焦到被测目标表面的光线才能通过接收狭缝到达探测器, 在zemax非序列模式下, 针对500、 550、 600和650 nm四个波长进行追迹, 上述四个波长在被测物表面聚焦时的光迹图如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
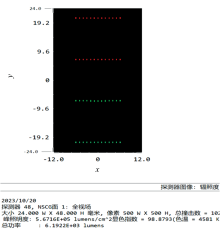	图11 光谱共焦线扫式测量系统整体光迹图Fig.11 Overall ray tracing of the line-scanning confocal spectral measurement system

全系统成像质量由探测器面上的光斑半径决定。 在zemax非序列模式下经光线追迹后在探测器面上可以获得光斑RMS半径值。 在工作波段500~650 nm范围内, 由探测器面上数据可知, 成像光斑半径均小于一个像元大小, 故成像质量满足要求。

由上述设计可知, 色散物镜色散范围为3 mm, 光谱仪光谱分辨率达到0.04 nm, 工作波段范围为500~650 nm, 代入式(5)可知位移分辨率至少为0.8 μ m。