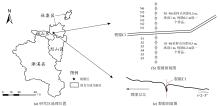
研究区位于安徽省淮北市朱庄煤矿3522工作面地表拉张裂隙区, 如图1所示, 土壤类型主要为潮土与半水成土纲的砂姜黑土。 受工作面回采影响, 在平行于工作面风巷、 下沉盆地坡地形成了拉张裂隙, 坡地北高南低, 坡度约2° ~3° 。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区位置及采样点布设Fig.1 Geographical location and sampling point layout of the study area

以C1裂隙为对象, 其东西走向长约70 m, 裂隙宽度范围2~15 cm。 垂直于C1裂隙分别向南、 北两方向每隔0.5 m布设一个采样点, 每点采样深度1 m, 裂隙以北、 以南分别间隔10和20 cm使用土钻分层方法采集一个土壤样本, 采样点布设如图1(b)所示。 共计采集90份土壤样本, 样本去除动植物残体和石砾, 经实验室风干、 研磨等处理, 过20目筛后装入袋中待测。 每份土样平均分为2份, 一份用于SOM含量测定, 一份用于光谱采集。

SOM含量采用实验室重铬酸钾外加热法测定。 在室内, 使用ASD FieldSpec4 测定样本光谱, 其波段范围350~2 500 nm, 波段间隔1 nm。 所用光源为50 W卤素灯, 距土样30 cm, 光源天顶角为45° , 光纤探头置于样本正上方5 cm处, 每个样本进行20次测量, 取平均值作为该样本的光谱数据。 使用ViewSpecPro 软件去除异常光谱, 最终得到88份土壤光谱数据。

光谱在350~399和2 451~2 500 nm等波段信噪比较低, 去除这两段光谱数据, 保留400~2 450 nm波段作为原始光谱。 为减弱杂散光、 基线漂移及背景噪声等对光谱数据的影响, 应用Savitzky-Golay卷积平滑后分别进行倒数之对数(inverse-log reflectance, LR)^[17]、 一阶导数(first order differential reflectance, FD)^[18]和连续统去除(continuum removal, CR)^[18]等3种光谱变换。

光谱指数通过不同波段之间的光谱反射率耦合计算得到, 波段组合具有协同效应, 相较于单波段, 具有更丰富的特征信息^[19]。 研究中, 首先按5 nm间隔重采样, 随后对4种光谱形式下的波段进行组合运算, 构建差值指数(difference index, DI)、 比值指数(ratio index, RI)和归一化指数(normalized difference index, NDI)等三种光谱指数, 其计算公式如式(1)— 式(3)

DI=Ri-Rj(1)

RI=Ri/Rj(2)

NDI=(Ri-Rj)(Ri+Rj)(3)

式(1)— 式(3)中, R_i和R_j分别代表i和j波段的土壤样本光谱反射率。

1.4.1 皮尔逊相关系数

皮尔逊相关系数(Pearson correlation coefficient, PCC)用于衡量两个变量X和Y之间的线性相关性, 其值介于-1~1 之间, 相关系数的绝对值越接近于1表示两个变量之间的线性相关性越强, 其中正值表示正相关, 负值表示负相关。 计算公式如式(4)

r=∑i=1n(xi-x̅)(yi-y̅)∑i=1n(xi-x̅)2∑i=1n(yi-y̅)2(4)

式(4)中, n为样本数, x̅和 y̅分别代表特征变量均值和目标变量均值。

1.4.2 最大相关最小冗余

在信息论中, 互信息(mutual Information, MI)用于衡量两个随机变量之间相互依赖程度^[20]。 互信息值越大, 两个随机变量之间的依赖性越强, 反之则表示它们之间的关联程度越低。 互信息定义如式(5)

I(x, y)=∑i, jP(xi, yj)logP(xi, yj)P(xi)P(yj)(5)

式(5)中, P(x_i)、 P(y_j)分别表示随机变量x、 y的概率密度, P(x_i, y_j)表示x、 y的联合概率密度, I(x, y)表示x与y之间的互信息。

最大相关最小冗余(maximum relevance minimum redundancy, mRMR)通过计算特征与目标变量之间的互信息以及特征之间的互信息, 来确定最佳的特征子集。

D(S, y)=1S∑xi∈SI(x, y)(6)

R(S)=1S|2∑xi, xj∈SI(xi, yj)(7)

maxϕ[D, R(S)], ϕ=D-R(S)(8)

式(6)— 式(8)中, D为特征与目标变量之间的互信息, R(S)为特征之间的互信息, |S|为特征个数, y为目标变量, x_i和x_j分别为特征集合中的元素, 代表最大相关最小冗余值。

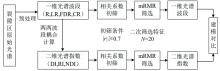
为保证训练集能代表样本的统计数据特征, 通过Kennard-Stone(KS)^[21]算法对88个样本数据进行划分, 选取2/3的样本作为训练集, 1/3的样本作为测试集。 在光谱特征选择中, 分别对光谱波段和构建的光谱指数独立进行筛选。 首先根据相关系数满足指定阈值的条件筛选光谱波段和光谱指数, 随后结合mRMR算法进一步提取敏感波段和敏感光谱指数, 作为输入变量构建裂隙区SOM含量估测模型, 其数据处理流程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 数据处理流程Fig.2 Flow chart of data processing

应用的模型分别是偏最小二乘回归(PLSR)和XGBoost, 模型的实现均基于Python 3.9.7软件。 PLSR是一种线性回归模型, 可有效解决变量之间的多重共线性问题。 XGBoost模型基于梯度增强方法开发改进, 核心是采用集成思想, 将多个弱学习器整合为一个强学习器^[18]。 PLSR的主成分数采用留一交叉验证法确定, XGBoost模型的参数通过随机搜索确定。 选用决定系数(determination coefficients, R²)、 均方根误差(root mean of squared error, RMSE)与相对分析误差(relative percent deviation, RPD)作为评价指标。 R²的值越接近1, RMSE越接近0, RPD越大, 模型的预测能力越好。

对裂隙区土壤样本SOM含量进行统计, 结果如表1所示。 经分析, 裂隙区SOM含量在0.26~7.06 g· kg^-1之间, 平均值为2.42 g· kg^-1, 依据全国第二次土壤普查养分分级标准, 对研究区88个土壤样品按养分的高低分为4个等级(> 5、 3~5、 2~3和< 2 g· kg^-1)。 SOM总体偏度呈正值, SOM含量属于非正态分布, SOM总体变异系数为61.32%, 根据土壤科学研究中变异系数对土壤性质变异程度的划分标准^[22], 其属于高等强度变异。

表1

Table 1

表1(Table 1)

表1 裂隙区SOM变异特征 Table 1 Statistics of soil organic matter content in fissures 样本类型 数量 最大值/ (g· kg-1) 最小值/ (g· kg-1) 平均值/ (g· kg-1) 标准差/ (g· kg-1) 变异系数/ % 偏度 总体 88 7.06 0.26 2.42 1.48 61.32 0.93 训练集 59 7.06 0.26 2.48 1.60 64.87 0.87 测试集 29 5.05 0.60 2.30 1.21 52.59 0.87

表1 裂隙区SOM变异特征 Table 1 Statistics of soil organic matter content in fissures

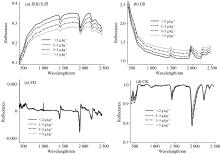
设置SOM含量> 5、 3~5、 2~3和< 2 g· kg^-1共4个区间范围, 计算各区间土壤光谱反射率平均值, 得到研究区土壤样本4个区间对应平均光谱曲线, 如图3所示。 图3(a)中, 不同SOM含量的土壤样本光谱曲线形态和走势相似, 但随着SOM含量的增加, 土壤光谱反射率逐渐降低, 在波段1 400、 1 900和2 200 nm处有三个明显的吸收谷, 其中1 400和1 900 nm处的吸收谷通常被认为与水分的吸收带有关^[23], 而波长为2 200 nm附近的吸收带主要是由于有机质中— OH官能团的伸缩振动和转角振动的合频跃迁引起^[24]。 此外, 在波段2 300 nm附近存在一个与有机质相关的C— H特征峰^[25]。 图3(b)— (d)为经过倒数之对数、 一阶导数和连续统去除等处理后的光谱曲线, 其光谱曲线的波谷和波峰更加突出。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同SOM含量的土壤光谱曲线Fig.3 Spectral curves of soil with different SOM content

2.3.1 土壤光谱与SOM的一维相关分析及波段筛选

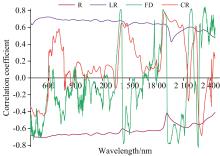
利用皮尔逊相关系数法计算原始光谱及LR、 FD、 CR光谱各波段反射率与SOM含量间的相关性, 结果如图4所示。 图4中, 原始光谱、 LR光谱与SOM含量的相关系数曲线变化较平缓, 其中原始光谱与SOM呈负相关, 而LR光谱呈正相关。 FD、 CR光谱与SOM含量的相关系数在零值附近波动, 曲线峰谷特征明显, 易于识别关键波段。 此外, FD、 CR光谱与SOM含量在部分波段上的相关性显著高于原始光谱和LR光谱, 其中最大相关系数分别达到0.85(1 878 nm)和0.78(2 340 nm), 而原始光谱和LR光谱的最大相关系数分别为0.71(528 nm)和0.72(579 nm)。 根据相关系数绝对值|r|≥ 0.7的标准, 初步选取波段数量分别为: 原始光谱144个波段, LR光谱207个波段, FD光谱262个波段, CR光谱54个波段。 为进一步减小冗余信息, 提高特征选择的代表性, 使用mRMR算法对满足相关性要求的波段进行优化筛选。 设置特征个数N为20, 选取的光谱波段参与后续建模。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 SOM含量与一维光谱波段的相关性Fig.4 Correlation between SOM content and one-dimensional spectral bands

筛选后的波段分布如图5, 由图5可分析出, 原始光谱中SOM特征波段主要集中在400~600 nm可见光波段, 与前人研究结果基本吻合^{[26, 27, 28, 29]}。 预处理后的光谱改变了SOM特征波段的分布。 LR光谱与原始光谱的特征波段基本一致, 主要集中在450~700 nm, 而FD预处理增强了1 300、 1 900、 2 200和2 300 nm波段处的相关性, CR预处理则增强了1 800~1 900 nm区间的相关性。 总之, FD预处理在增强波段的相关性方面表现更为突出, 不仅保留了400~600 nm 波段有效信息, 还使近红外区域(1 300~2 500 nm)新的敏感波段得以显现。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 特征波段分布Fig.5 Distribution of characteristic bands

2.3.2 基于一维光谱波段的SOM估算结果

利用R、 LR、 FD和CR的特征波段建立裂隙区SOM含量的回归模型, 结果如表2所示。 基于一阶导数光谱的回归模型效果最好, PLSR和XGBoost模型测试集的R²分别为0.73和0.78; 基于原始光谱和LR光谱的回归模型预测效果一般, R²均大于0.6小于0.7; 基于CR光谱的回归模型的预测能力较差, 其测试集的R²均不足0.6。 总体来看, 基于FD光谱的XGBoost模型效果最好, 其RPD大于2.0, 能够实现裂隙区SOM含量的估测。

表2

Table 2

表2(Table 2)

表2 不同估算模型预测精度 Table 2 The prediction accuracy of different estimation models 模型 训练集 测试集 R2 RMSE/ (mg· kg-1) R2 RMSE/ (mg· kg-1) RPD R-PLSR 0.59 1.02 0.60 0.75 1.59 R-XGBoost 0.76 0.78 0.69 0.67 1.78 LR-PLSR 0.61 1.0 0.65 0.70 1.69 LR-XGBoost 0.73 0.83 0.65 0.71 1.69 FD-PLSR 0.79 0.73 0.73 0.61 1.94 FD-XGBoost 0.94 0.40 0.78 0.56 2.11* CR-PLSR 0.62 0.98 0.59 0.76 1.56 CR-XGBoost 0.88 0.55 0.59 0.76 1.56

表2 不同估算模型预测精度 Table 2 The prediction accuracy of different estimation models

2.4.1 土壤光谱与SOM的二维相关分析及光谱指数筛选

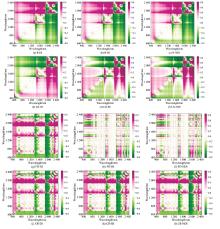
图6为研究区SOM含量与不同波段组合的光谱指数的相关性图, 展示了各波段组合的相关性强度分布。 在原始光谱中[图6(a)— (c)], SOM含量与DI相关性较高的波段组合主要分布在1 900~2 400 nm处, 相关性最高的波段组合为2 365和2 305 nm, 相关系数为0.855。 SOM含量与RI和NDI相关性较高的波段组合范围与DI一致, 但相关系数绝对值稍低, 最大相关系数分别为0.822和0.821。 在LR光谱中[图6(d)— (f)], SOM含量与DI、 RI、 NDI相关性较高的波段组合分布与原始光谱一致, 与DI的相关性不如与RI、 NDI的相关性高, 最大相关系数仅为0.821, 对应的波段组合是2 210和2 280 nm。 SOM含量与RI和NDI的相关系数绝对值均高达0.857。 在FD和CR光谱中[图6(g)— (l)], 相关性较高的波段组合分布散且范围窄, SOM与DI、 RI和NDI的相关性图分布一致。 FD光谱与SOM相关系数比CR高, 其中FD光谱的差值指数DI与SOM相关性最高, 相关系数最大为0.879, 对应的波段组合为1 340和2 255 nm。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 SOM含量与不同预处理二维光谱指数的相关性Fig.6 Correlation between SOM content and two-dimensional spectral index

表3中列出了光谱指数与SOM含量相关性最大的波段组合, SOM与光谱指数的相关系数比一维光谱波段高。 一维光谱对SOM的响应在可见光区域, 这主要源于有机色团(如胡敏酸)和金属氧化物的电子跃迁效应。 光谱指数则在1 900~2 400 nm波段组合处与SOM含量具有强相关性, 这是由于该区域能捕获有机分子中C— H、 N— H等化学键的分子振动及有机矿物相互作用等复合特征^[30]。 可见光区主要反映SOM的表观颜色特征, 而短波红外组合则更直接关联有机质的分子组成和官能团信息^[31]。 选择与SOM相关系数绝对值|r|≥ 0.7的光谱指数, 并利用mRMR算法进一步对光谱指数筛选。 设置特征个数N为20, 选取的光谱指数参与后续建模。

表3

Table 3

表3(Table 3)

表3 不同光谱指数的SOM敏感光谱指数统计 Table 3 The statistics of SOM sensitive spectral indices of different spectral indices 光谱指数 |r|最大值 |r|最大值对应波段组合 DI 0.88 FD1 340-FD2 255 RI 0.86 LR2 365/LR2 300 NDI 0.86 (LR2 365-LR2 300)/(LR2 365+LR2 300)

表3 不同光谱指数的SOM敏感光谱指数统计 Table 3 The statistics of SOM sensitive spectral indices of different spectral indices

2.4.2 基于二维光谱指数的SOM估算结果

利用R、 LR、 FD和CR光谱的DI、 RI、 NDI三种光谱指数建立采煤拉张裂隙区SOM含量的估算模型, 具体结果见表4。 原始光谱构建的模型中DI-PLSR模型效果最好, 测试集R²为0.79, RMSE为0.53 mg· kg^-1, RPD为2.26; LR、 CR光谱构建的模型效果较原始光谱提升不大, 测试集的最大R²分别为0.78、 0.76, 对应的模型分别是是LR-RI-XGBoost、 CR-RI-XGBoost; FD光谱构建的模型测试集RPD均大于2.0, 相比于其他光谱数据建立的模型估算效果较好。 经分析得出, FD-NDI-XGBoost模型效果最好, 其测试集R²为0.83、 RMSE为0.49 mg· kg^-1、 RPD为2.44。

表4

Table 4

表4(Table 4)

表4 不同估算模型预测精度 Table 4 The prediction accuracy of different estimation models 光谱形式 光谱指数 模型算法 训练集 测试集 R2 RMSE/(mg· kg-1) R2 RMSE/(mg· kg-1) RPD R DI PLSR 0.86 0.59 0.79 0.55 2.17 XGBoost 0.94 0.38 0.74 0.61 1.96 RI PLSR 0.86 0.59 0.75 0.59 2.01 XGBoost 0.94 0.38 0.71 0.64 1.86 NDI PLSR 0.87 0.58 0.72 0.62 1.91 XGBoost 0.94 0.39 0.72 0.63 1.89 LR DI PLSR 0.88 0.54 0.75 0.60 1.99 XGBoost 0.93 0.43 0.71 0.64 1.86 RI PLSR 0.80 0.71 0.74 0.60 1.99 XGBoost 0.99 0.11 0.78 0.56 2.14 NDI PLSR 0.79 0.72 0.73 0.62 1.92 XGBoost 0.96 0.31 0.77 0.57 2.08 FD DI PLSR 0.84 0.65 0.81 0.51 2.32 XGBoost 0.98 0.22 0.82 0.51 2.33 RI PLSR 0.81 0.70 0.77 0.56 2.11 XGBoost 0.94 0.39 0.79 0.55 2.17 NDI PLSR 0.82 0.68 0.82 0.51 2.34 XGBoost 0.95 0.37 0.83 0.49 2.44* CR DI PLSR 0.77 0.76 0.71 0.64 1.87 XGBoost 0.94 0.38 0.74 0.60 1.96 RI PLSR 0.82 0.68 0.73 0.61 1.94 XGBoost 0.91 0.47 0.76 0.58 2.06 NDI PLSR 0.82 0.68 0.73 0.62 1.93 XGBoost 0.94 0.39 0.73 0.62 1.91

表4 不同估算模型预测精度 Table 4 The prediction accuracy of different estimation models

综合评估R、 LR、 FD、 CR四种光谱数据, 并对比一维光谱波段与二维光谱指数建立的SOM预测模型, 模型评价指标如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同模型的评价指标(None: 一维光谱)Fig.7 Evaluation indexes of different models (None: 1D spectra)

对于不同预处理后的光谱数据, 研究区SOM含量模型估测效果依次为FD> LR≈ R> CR。 其中, FD处理能显著提升模型的估测精度, 其一维光谱波段模型R²> 0.73, 较原始光谱模型(R²> 0.60)提升21.7%; 光谱指数模型R²> 0.77, 较原始模型(R²> 0.71)提升8.5%。 这主要与FD处理能有效抑制土壤背景噪声和基线漂移有关^[20]; 一维光谱波段与二维光谱指数对比分析表明, 基于光谱指数构建的模型预测精度显著优于一维光谱波段模型, 这主要由于光谱指数通过特定波段的非线性耦合不仅能放大有机质特征波段的响应, 更能有效捕捉化学键振动及有机矿物相互作用等复合特征^{[30, 31]}; 从模型的角度来看, PLSR和XGBoost均表现良好, 基于XGBoost的模型精度略高于PLSR模型, 这可能源于XGBoost算法独特的建模过程, 其基于决策树的集成学习框架能够通过自适应处理非线性关系, 并利用boosting策略优化特征交互, 从而更有效地挖掘光谱数据的深层特征^[18]。 原始光谱反射率范围较大, 数值均为正值且差异明显, 适合构建差值指数DI; FD光谱值范围较小, 包含正负值, 归一化处理可以消除量纲影响, 能有效放大其微分后的特征差异。