柴油十六烷值近红外系统受控下数据质量目标的优化

引用本文

李颖, 潘志强, 王斗文. 柴油十六烷值近红外系统受控下数据质量目标的优化[J]. 光谱学与光谱分析, 2025,45(9): 2535-2542.
LI Ying, PAN Zhi-qiang, WANG Dou-wen. Optimization of Data Quality Objectives Under Control of Near Infrared System for Diesel Cetane Number[J]. Spectroscopy and Spectral Analysis, 2025,45(9): 2535-2542.
Doi:10.3964/j.issn.1000-0593(2025)09-2535-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

柴油十六烷值近红外系统受控下数据质量目标的优化

李颖¹, 潘志强², 王斗文^3,^*

1.大连产品质量检验检测研究院有限公司, 辽宁大连 116021

2.大连西太平洋石油化工有限公司, 辽宁大连 116600

3.大连海关技术中心, 辽宁大连 116001

*通讯作者 e-mail: wangdouwen@163.com

作者简介: 李颖,女, 1976年生,大连产品质量检验检测研究院有限公司高级工程师 e-mail: 819818501@qq.com

收稿日期: 2025-03-26 修回日期: 2025-06-24 接受日期: 2025-06-24

基金: 国家标准委科学基金项目(20211977-T-469)资助

摘要

柴油十六烷值近红外(NIR-CN)系统测试的数据质量目标(DQO)建模优化, 目前尚未见到成熟的研究成果。为减轻匹配错误的综合基体效应和避免单水平无法控制的β风险, 本工作利用美国瓦克夏(Waukesha)十六烷值机数据进行比对。经与幂律、二次线性组合和斜率弧度的统计比较, 认为最大似然估计戴明回归(DR)的偏倚修正属于最佳合理拟合模型。 DR建模来自水平下加权中心平方和(CSS)二维数据的变量迭代, 其建立在随机变量独立同分布(i.i.d)假设检验的前提条件, 非视相关系数为模型拟合优劣的判断依据, 而是通过失拟效应和Anderson-Darling(AD)拟合优度检验。这种检验能有效避免自相关函数(ACF)的累积冲击和交互干扰, 最大限度弥补控制图主观臆断趋势分析的目测不足。研究结果表明, DR模型更符合NIR系统的DQO稳健性和实际情况。 NIR系统以往仅局限于CN单一水平讨论, 现扩展到多个水平的变异研究。不同决策导致不同不确定度, 错误决策会遭致额外的成本损失。随时间推移在风险与成本统一的原则下难免会出现CSS的重新选择, 只要后续测试满足NIR系统所设定的DQO随机扰动, 将使用条件产生的风险控制在所论证的CSS范围内即可。

关键词: 数据质量目标; 戴明回归; 加权中心平方和; 失拟效应; 独立同分布; 自相关函数

中图分类号:O657.31 文献标志码:A

Optimization of Data Quality Objectives Under Control of Near Infrared System for Diesel Cetane Number

LI Ying¹, PAN Zhi-qiang², WANG Dou-wen^3,^*

1. Dalian Product Quality Inspection and Testing Institute, Dalian 116021, China

2. West Pacific Petrochemical Company, Dalian 116600, China

3. Dalian Customs Technical Center, Dalian 116001, China

*Corresponding author

Abstract

The DQO modeling for the NIR-CN system has not yet seen mature research results, in which comparison with data from the Waukesha CN engine was conducted to alleviate the composite matrix effect of matching error and the uncontrollable β risk at a single level. Compared to the power function, quadratic linear combination, and slope radian angles, the DR bias correction model's maximum likelihood estimate is found to be the best-fitting line. The DR modeling, which was derived from the variable iteration of two-dimensional data weighted by the CSS, was established under the premise of the i.i.d. assumption. Consequently, the correlation coefficient cannot be regarded as the criterion for judging the model, but rather through the lack of fit and the AD goodness-of-fit test. This test can effectively mitigate the cumulative impact and interaction interference of ACF, and maximize compensation for the limitations of subjective trend analysis in control charts. The research results indicate that the DR model aligns more closely with the DQO robustness and the actual situation of the NIR system. The NIR system was previously limited to a single CN level discussion; now it has been expanded to study variations at multiple levels. Different decisions lead to different uncertainties, and wrong decisions will incur additional cost losses. Under the uniform principle of risk and cost, the variation of CN over time will inevitably lead to the choice of CSS. As long as the DQO set by the NIR system is subsequently met, the risk arising from the use conditions can be controlled within the demonstrated CSS range.

Keyword: Data quality objectives; Deming regression; Centered Sum of Squares; Lack of fit; Independence identical distribution; Autocorrelation function

文章图片

引言

在柴油CN测试中, NIR系统(常规方法, 以下简称X法)是一种多元过程的关联模型测试, 常被用来替代笨重且昂贵的Waukesha十六烷值机操作(参考方法, 以下简称Y法)^[1]。在承担柴油调和的CN检验市场中, 在节能降费、提质增效与风险的折中权衡, X法起到了不可忽视的重要作用。

基于Y法对X法的确认, 两种方法的测试原理完全不同。无需努力评估两者分析技术的近似程度, 而是寻找其结果之间的一致性。为降低人为偏性的实验方案设计需斟酌可用资源的分配, 双总体配对的分割水平采用, 能减少外界条件变化所产生的不同影响。这种类似于随机处理的完全区组设计会涵盖更多变异源, 有助于总体误差之间的相互独立和偏离监控。

协同试验和能力验证非误差控制的有效方式, 重复性(r)太理想而再现性(R)过于保守, 本工作利用X法系统受控下的室内再现性(intermediate limit, R'), 最大限度覆盖时间和空间的广义重复, 以获得更多信息来推断总体^{[2, 3, 4, 5]}。 X法和Y法之间的关联性不等于因果关系, 而是受制于某些隐藏的混杂影响因素所致, 尤其是当产生基质和交互效应作用时, 很难将其排除掉, 极易导致X法和Y法两者间拟合模型的失败。然而, 当下某些学者一味地视相关系数为模型拟合优劣的判断依据, 可否将其理解为是一种仅可参考的商榷思路。

本工作根据汇集X法和Y法的CN数据集, 经坐标变换后论证, 幂律、二次线性组合和斜率弧度统计均无法完成数据的自相关分析和偏倚修正。经审慎的比较和思考, X法的DQO优化可考虑DR模型的CSS处理, 这种处理属于多单元等概率的分割水平时序设计, 最大限度代表已知或潜在变异源的预期总变异, 有助于较大范围内有价值的推断和预测、以及现行系统的改进和风险控制。

NIR-CN测试系统研究的前提条件是, 满足线性可加模型的随机化设计、以及避免交互作用产生的相关性趋势。这种i.i.d状态的判断依然困扰目前的研究者。当下频繁采用主观臆断的目测分析, 实属非纯粹意义上的假设检验。为达到i.i.d的受控状态, 本工作利用AD拟合优度的检验^{[6, 7, 8, 9]}, 为解消假设的风险预控、优化组合的有效决策和随机化处理提供了更合理的估计。

当采用DR回归模型进行偏倚修正时, 各种处理随区组不同容易质疑交互作用, 此时的NIR-CN系统必须实施AD检验, 以判断机遇的解消假设是否成立。

NIR-CN系统受控下的DQO靠不确定度度量。为避免不确定度分析产生错误的结论, 不能仅停留在单水平估计的局限认知, 而是依靠多水平变异监控来支撑。在坚持质量效益与客户需求一致性的原则下, 合理的不确定度宜为特定水平下给出最小成本的理想估计。

1 实验部分

1.1 交互效应分析与幂律模型建立

本工作针对某X法系统的CN长期测试中, 自实验室信息管理系统LIMS随机抽取了6人次提交的4水平样数据对结果(X法和Y法各自提交独立结果)。见表1和表2。

表1 某X法与Y法的CN数据对变换 Table 1 CN data pair transformation of X method and Y method

表2 交互效应检查与幂律建模 Table 2 Interaction checking and power modeling

表1分别给出重复性标准差(s_r)和室内再现性标准差(s_R')。避免s_R'/s_r之比出现水平依赖性, 利用s_R'的对数关系寻找变换参数, 使得其效益化符合最佳加权拟合预测的估计。变换后的数据集必须通过式(1)的AD拟合优度检验, 式(1)中, AD分为AD_s(判断正态性和分辨力)和AD_MR(判断独立性), AD_MR计算有移动极差(MR)^[10], p_i为结果的累积正态概率。

$AD = \{\frac{- \sum (2_{i} - 1) [\ln (p_{i}) + \ln (1 - p_{n + 1 - i})]}{n} - n\} \times$

$(1 + \frac{0.75}{n} + \frac{2.25}{n^{2}})$ (1)

表1中有, s_R'/s_r模型有p(斜率)< 0.05, 因无数据丢失可不必对s_r变换。但s_R'具不等自由度的效应, 可寻找其最佳的变换估计参数。变换值近似有 $\sqrt[]{X}$ 和 $\sqrt[]{Y}$ (省略积分常数)。变换后的数据集经广义极值学生化偏差(GESD)技术检查, 未发现存在离群值。 AD_s=0.462< 0.752, 接收系统的正态性假设。

表2为交互效应分析和系统性能建模, 按式(2)— 式(4)计算。 s'²(单元间方差)见式(2), 其中的a=X+Y, n=2, S为每个样品所得结果的总数, P为参加人次。

$s'^{2} = \frac{\sum \frac{{(a)}^{2}}{n} - \frac{{(\sum a)}^{2}}{S}}{P - 1}$ (2)

R'²见式(3), 其中, β= $\frac{PS - S}{P - 1}$ ; M_P、 M_PS和M_r分别为人次、交互和重复均方。

$R'^{2} = \frac{2}{β} M_{P} + (1 - \frac{2}{β}) M_{PS} + M_{r}$ (3)

R'(原结果)见式(4), 其中 $|\frac{d (原结果)}{d (变换值)}|$ 为求导。

$R^{'} (原结果) = |\frac{d (原结果)}{d (变换值)}| R^{'} (变换值)$ (4)

表2的F比值结果确保了交互作用影响减至最小。根据式(2)— 式(4)求得R'(XY)=2.48 ${\bar{XY}}^{0.6}$ × t $\sqrt[]{R'^{2}}$ , 其中R'²来自式(3)的计算有0.003, 基于此, 自由度42由Welch-Satterthwaite式求得。修正值1141.1来自 $\frac{{(\sum a)}^{2}}{全部结果} 。$

通过交互效应的评价建立了方法间的性能R'(XY)=0.26 ${\bar{XY}}^{0.6}$ , 但该性能无法对数据的自相关和偏倚做判断。

1.2 二次函数与斜率弧度等效探讨

基于表1的数据集, 表3给出了二次线性组合和斜率弧度的统计拟合。

表3 二次线性组合与斜率弧度的检查 Table 3 Check of quadratic linear combinations and slope radian

No	Y=62.34-1.27X+0.02X²								方法间斜率弧度统计
No	X	X²	X³	X⁴	Y	XY	X²Y	p(s)	(X- $\overset{̅}{X}$ )(Y- $\overset{̅}{Y}$ )	p(s)
1	46.6	2 172	101 195	4 715 673	45.5	2 120.30	98 806	0.074	19.39	0.132
2	47.3	2 237	105 824	5 005 467	45.9	2 171.07	102 692	0.069	14.69	0.102
3	45.4	2 061	93 577	4 248 381	47.5	2 156.50	97 905	0.784	14.71	0.901
4	45.8	2 098	96 072	4 400 094	47	2 152.60	98 589	0.574	16.00	0.732
5	47.4	2 247	106 496	5 047 930	46.6	2 208.84	104 699	0.169	11.99	0.218
6	45.1	2 034	91 734	4 137 197	47	2 119.70	95 598	0.697	18.32	0.862
7	48.1	2 314	111 285	5 352 791	48.5	2 332.85	112 210	0.587	4.58	0.603
8	49.9	2 490	124 251	6 200 150	48.6	2 425.14	121 014	0.224	1.25	0.191
9	48.3	2 333	112 679	5 442 376	49.6	2 395.68	115 711	0.844	1.66	0.842
10	50.7	2 570	130 324	6 607 419	49.9	2 529.93	128 267	0.422	-0.03	0.353
11	50.3	2 530	127 264	6 401 355	49	2 464.70	123 974	0.248	0.43	0.205
12	48.2	2 323	111 980	5 397 444	50.1	2 414.82	116 394	0.930	0.52	0.929
13	52.6	2 767	145 532	7 654 961	51.2	2 693.12	141 658	0.339	1.75	0.267
14	52.2	2 725	142 237	7 424 753	50.1	2 615.22	136 514	0.150	-0.33	0.109
15	52	2 704	140 608	7 311 616	53	2 756.00	143 312	0.931	3.68	0.888
16	50.2	2 520	126 506	6 350 602	51	2 560.20	128 522	0.848	-0.30	0.799
17	52.5	2 756	144 703	7 596 914	51.1	2 682.75	140 844	0.335	1.47	0.263
18	52.2	2 725	142 237	7 424 753	50.5	2 636.10	137 604	0.239	0.29	0.181
19	55.9	3 125	174 677	9 764 438	53.5	2 990.65	167 177	0.148	16.80	0.155
20	55.3	3 058	169 112	9 351 914	54	2 986.20	165 137	0.441	17.22	0.416
21	53.7	2 884	154 854	8 315 668	54.9	2 948.13	158 315	0.966	14.09	0.943
22	55	3 025	166 375	9 150 625	53.1	2 920.50	160 628	0.257	12.18	0.233
23	55.5	3 080	170 954	9 487 940	54.2	3 008.10	166 950	0.442	18.94	0.425
24	54.9	3 014	16 5469	9 084 256	55.7	3 057.93	167 880	0.941	23.01	0.921
p(s)为AD_s的正态概率值, 见式(1)
AD_s								0.529		1.136
偏差平方和	271.8				200.8				212.3

表3 二次线性组合与斜率弧度的检查 Table 3 Check of quadratic linear combinations and slope radian

表3的二次函数尽管接收AD的解消假设, 但回归参数对Y影响不大。

表3中的斜率弧度计算见式(5)和式(6)。

$β = \frac{S_{YY} - S_{XX} + \sqrt[]{(S_{YY} - S_{XX})^{2} + 4 S_{XY}^{2}}}{2 S_{XY}}$ (5)

$CL = θ \pm 0.5 \arcsin [t_{n - 2, 0.95} \frac{2}{\sqrt[]{n - 2}} \sqrt[]{\frac{S_{YY} S_{XX} - S_{XY}^{2}}{(S_{YY} - S_{XX})^{2} + 4 S_{XY}^{2}}}]$ (6)

式(5)和式(6)中, β为斜率; S_XX、 S_YY和S_XY分别为X法和Y法的数据偏差平方和、以及两个变量协方差。

为验证方法间斜率的等效结果, 利用坐标旋转变换的弧度法, 通过正交最小二乘线性关系的角度盘, 将数据反变换为原尺度。表3利用式(5)和式(6)求得, b(斜率)=0.849和a(截距)=7.446; ϕ=0.117 3; θ(弧度角)=0.702 6(与0.785 4有差异)。由此求得上限和下限有LCL(θ)=0.585和UCL(θ)=0.820, 进而给出LCL(β)=0.66和UCL(β)=1.07。接受(0.75-1.33)斜率等效假设, 但AD评价该模型系统失控。

	Figure Option View Download New Window
	图1 方法间斜率正交回归的弧度检查Fig.1 The radian check of slope orthogonal regression between different methods

1.3 DR模型的选择与评价

1.3.1 CSS的理解

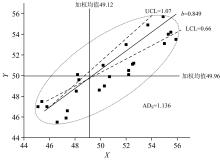
在柴油过程流体的CN分析中存在太多的变量, 确保测试系统的i.i.d状态不是一件容易的事情。毕竟X法属于非标系统, 最佳的办法是同时估计X和Y的误差, 找准残差变量间的函数关系f(x), 考察实际X与理论Y的符合程度, 确立X法实时测量的一致性和可靠性。见图2。

	Figure Option View Download New Window
	图2 方法间CSS拟合Fig.2 CSS fits between different methods

图2的解释有如下说明:

无偏函数有 $CS S_{0} = \sum w {(Y - X)}^{2}, 其中 w = 1 / (S_{X}^{2} + S_{Y}^{2})$ 。

常数函数有 $S S_{1} = \sum w [Y - {(X + a)]}^{2}$ , 其中 $a$ 为截距, $w = 1 / (S_{X}^{2} + S_{Y}^{2})$ 。

鉴于CN的0特性值无物理意义, 故未纳入比例函数的CSS拟合。

线性函数检验是否符合随机变量 $y$ 与 $x$ 之间的实际关系, 其函数关系有 $CS S_{2} = \sum w {(y - bX)}^{2}$ , 其中 $w = 1 / (S_{Y}^{2} + b^{2} S_{X}^{2}), x_{i} = X_{i} - \overset{̅}{X}$ (权值)和 $y_{i} = Y_{i} - \overset{̅}{Y}$ (权值)。 $b$ 斜率由二次函数求根迭代逼近, 其阈值收敛为0.001b。

1.3.2 DR模型的有效性评价

自LIMS系统在45-56(CN)水平范围内, 前一个阶段按时间序列随机抽取了X法和Y法水平下20个数据对结果, 见表4。

表4 两个阶段数据对的CSS评价与选择 Table 4 CSS evaluation and selection of data pairs for two phases

No	X	S_X	Y	S_Y	ω	CSS₀	ω X	ω Y	CSS₁	x	y	ω	ω X	ω Y	CSS₂	p(s)	p(MR)	Δ	Z(X)	评判
1	46.6	0.77	45.5	1.24	0.47	0.57	21.9	21.4	0.65	-3.41	-4.59	0.58	26.9	26.2	4.03	0.52	0.52	19.0	1.3	1.3
2	52.5	1.16	51.1	1.41	0.30	0.59	15.8	15.4	0.66	2.49	1.01	0.41	21.7	21.1	0.07	0.30	0.29	21.2	1.2	2.5
3	55.9	1.38	53.5	1.48	0.24	1.40	13.6	13.0	1.50	5.89	3.41	0.36	19.9	19.0	0.00	0.14	0.13	21.7	1.7	4.2
4	45.8	0.71	47.0	1.29	0.46	0.67	21.2	21.7	0.58	-4.21	-3.09	0.55	25.1	25.8	0.26	0.82	0.83	20.9	-1.6	-1.6
5	51.2	1.07	52.9	1.46	0.30	0.88	15.6	16.1	0.80	1.19	2.81	0.40	20.4	21.1	1.81	0.69	0.70	23.8	-1.5	-3.1
6	45.1	0.67	46.3	1.27	0.49	0.70	22.0	22.6	0.61	-4.91	-3.79	0.57	25.8	26.5	0.56	0.83	0.84	20.6	-1.7	-4.7
7	48.8	0.91	51.5	1.42	0.35	2.56	17.1	18.1	2.41	-1.21	1.41	0.44	21.3	22.5	1.93	0.85	0.86	23.7	-2.8	-7.5
8	52.6	1.16	51.2	1.41	0.30	0.59	15.7	15.3	0.66	2.59	1.11	0.41	21.6	21.0	0.06	0.30	0.29	21.3	1.2	1.2
9	55.3	1.34	54.0	1.49	0.25	0.42	13.7	13.4	0.47	5.29	3.91	0.35	19.6	19.2	0.28	0.24	0.23	22.5	0.9	2.1
10	50.7	1.04	48.7	1.34	0.35	1.40	17.7	17.0	1.51	0.69	-1.39	0.47	23.7	22.8	1.49	0.28	0.27	19.9	1.9	4.0
11	47.6	0.83	50.2	1.38	0.38	2.60	18.3	19.3	2.44	-2.41	0.11	0.47	22.3	23.5	1.03	0.87	0.88	23.1	-2.9	-2.9
12	48.2	0.87	50.1	1.38	0.38	1.36	18.1	18.8	1.24	-1.81	0.01	0.47	22.4	23.3	0.51	0.81	0.82	22.7	-2.1	-5.0
13	49.9	0.99	48.6	1.33	0.36	0.61	18.1	17.7	0.69	-0.11	-1.49	0.48	23.8	23.2	0.97	0.39	0.38	20.2	1.3	1.3
14	52.2	1.14	50.3	1.38	0.31	1.12	16.3	15.7	1.22	2.19	0.21	0.43	22.3	21.5	0.46	0.25	0.24	20.6	1.6	2.9
15	52.0	1.12	54.8	1.52	0.28	2.20	14.6	15.4	2.07	1.99	4.71	0.37	19.2	20.2	4.71	0.77	0.78	25.2	-2.4	-2.4
16	50.3	1.01	49.0	1.35	0.35	0.60	17.7	17.3	0.67	0.29	-1.09	0.47	23.5	22.8	0.74	0.37	0.37	20.4	1.2	1.2
17	48.4	0.89	47.5	1.30	0.40	0.33	19.5	19.2	0.39	-1.61	-2.59	0.51	24.8	24.4	1.43	0.49	0.49	20.0	1.0	2.2
18	55.8	1.38	54.3	1.50	0.24	0.54	13.4	13.1	0.60	5.79	4.21	0.35	19.4	18.9	0.29	0.21	0.20	22.5	1.1	3.3
19	47.4	0.82	45.6	1.25	0.45	1.46	21.3	20.5	1.59	-2.61	-4.49	0.57	26.8	25.8	5.09	0.40	0.40	18.6	2.1	5.3
20	53.8	1.24	52.2	1.44	0.28	0.71	14.9	14.4	0.78	3.79	2.11	0.39	20.9	20.2	0.00	0.25	0.24	21.6	1.2	6.6
21	51.7	1.10	53.0	1.46	0.30	0.50	15.4	15.8	0.44	1.69	2.91	0.39	20.3	20.9	1.49	0.63	0.64	23.6	-1.1	-1.1
22	48.7	0.91	51.6	1.42	0.35	2.96	17.1	18.1	2.80	-1.31	1.51	0.44	21.3	22.5	2.22	0.86	0.87	23.9	-3.0	-4.1
23	53.6	1.23	51.4	1.42	0.28	1.37	15.2	14.6	1.48	3.59	1.31	0.40	21.4	20.6	0.22	0.20	0.19	20.9	1.7	1.7
24	56.3	1.41	52.4	1.45	0.25	3.73	13.8	12.8	3.89	6.29	2.31	0.37	20.5	19.1	0.60	0.06	0.05	20.4	2.7	4.4
25	45.2	0.67	49.5	1.36	0.43	8.03	19.6	21.5	7.73	-4.81	-0.59	0.50	22.6	24.8	2.32	0.97	0.98	23.8	-5.8	-5.8
26	54.5	1.29	51.5	1.42	0.27	2.45	14.8	14.0	2.58	4.49	1.41	0.39	21.3	20.1	0.52	0.12	0.11	20.5	2.3	2.3
27	46.9	0.79	50.3	1.38	0.39	4.56	18.5	19.9	4.35	-3.11	0.21	0.47	22.2	23.8	1.86	0.92	0.93	23.6	-4.0	-4.0
28	45.3	0.68	49.7	1.37	0.43	8.31	19.5	21.3	8.01	-4.71	-0.39	0.50	22.5	24.6	2.61	0.97	0.98	23.9	-5.9	-9.9
29	55.6	1.36	51.8	1.43	0.26	3.70	14.3	13.3	3.86	5.59	1.71	0.38	21.0	19.6	0.83	0.07	0.06	20.2	2.7	2.7
30	54.6	1.30	51.1	1.41	0.27	3.34	14.9	13.9	3.50	4.59	1.01	0.40	21.6	20.2	1.02	0.09	0.08	20.0	2.6	5.3
AD																0.564	0.658
$\overset{̅}{Z}$ (X)																			-0.2
CSS						60.3			60.2						39.4
χ²	43.8			42.6											41.3

注: (1): S_X为X法的标准差, S_Y为Y法的标准差, 各水平下的标准差通过插值求得, 方法间的变异RSD≤ 5%; (2): p(s)为AD_S的正态概率值; p(MR)为AD_MR的正态概率值

Note: (1) The RSD≤ 5% betwwen X and Y methods, with their S_X and S_Y calculated by interpolations; (2): p(s) and p(MR) represent the normal probability values of AD_S and AD_MR

表4 两个阶段数据对的CSS评价与选择 Table 4 CSS evaluation and selection of data pairs for two phases

表4中的解消假设为CSS₀, 而更多的是备择假设。通过加权迭代的函数权重推导, 进行数学变换和线性修匀的平滑逼近。方法间CSS残差加权回归量化的选择计算有如式(7)和式(8)判断公式。

$F = \frac{(CS S_{0} - CS S_{2} \frac{)}{2}}{CS S_{2} / (S - 2)}$ (7)

$t_{1} = \sqrt[]{\frac{CS S_{0} - CS S_{1}}{CS S_{2} / (S - 2)}}, t_{2} = \sqrt[]{\frac{CS S_{1} - CS S_{2}}{CS S_{2} / (S - 2)}}$ (8)

式(7)的F为失拟效应检查, 可通过F单侧备择假设判断; 式(8)中若t₂接受备择假设则选CSS₂, 反之看CSS₁。若t₁绝原假设选择CSS₁, 反之用CSS₂。

$ε = \sqrt[]{w} (Y - \hat{Y})$ (9)

式(9)的ε为所选CSS模型的系列残差; w为所选CSS模型的加权值; $\hat{Y}$ 为所选CSS模型的Y拟合值。

在表4中, 前一个阶段按时序抽取的20个数据对, 利用功效0.90的双单侧区间Δ偏倚检查, 发现超出业内设定的± 3, 方法间需建立偏倚修正。因式(8)的计算有t₂=1.28和t₁=0.50, 均小于t临, 则选择Y=0.83X-0.22的拟合, 且CSS₂=19.27< χ²=28.9。

但由式(7)得知F=0.95< 3.55, 表明Y=0.83X-0.22无法改进X法和Y法的一致性。更严重的是, 由式(1)和式(9)给出AD_s=1.607和AD_MR=2.732, 完全拒绝系统具有良好的正态性、分辨力和独立性假设。

在表4第一阶段数据集的基础上, 后续跟进增加了10对时序数据, 形成第二阶段的30个数据对。

尽管表中的Z(X)标准评分有 $\overset{̅}{Z}$ (X)=-0.2, 但其评判(相同符号下Z分数的加合)暗指, 几个数据对有偏倚。功效0.90的双单侧区间Δ偏倚检查, 超出业内设定的± 3, 方法间需建立偏倚函数修正。

表4中的CSS₂最终求得b=0.570 3, a=-0.071。由式(7)和式(8)得知, F=4.76> 3.34, t₂=3.08> 2.05, 即利用Y=0.57X-0.07(CSS₂=39.4< χ²=41.3), 可以改进X法和Y法之间的预期一致性。

由式(1)和式(9)给出AD_s=0.564和AD_MR=0.658, 表明95%概率下方法间残差系统的良好正态性、分辨力和独立性假设成立。

DR模型的性能评价见式(10)

$R'_{XY} = \sqrt[]{\frac{b^{2} R'_{X}^{2}}{2} + \frac{R'_{Y}^{2}}{2}}$ (10)

其中的R'(XY)为方法间共享的室内再现性; b为所选CSS模型的斜率。

表4有模型s(X)=0.66+0.07(X-45)和s(Y)=1.23+0.03(Y-45)。根据式(10), 两个模型经合并整理后有R'(XY)= $\sqrt[]{0.006 {(X - 35.6)}^{2} + 0.003 5 {(Y - 4)}^{2}}$ 。

Y法规定的R^[1](括号内为CN值)有: 40(2.8), 44(3.3), 48(3.8), 52(4.3)和56(4.8), 见图3。

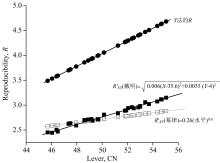	Figure Option View Download New Window
	图3 幂律和DR模型受控下45-56(CN)水平测试的DQO性能比较Fig.3 Comparison of DQO performance on 45-56 (CN) testing from power and DR model in control

图3中给出R'(XY)=0.26 ${\bar{XY}}^{0.6}$ 和R'(XY)= $\sqrt[]{0.006 {(X - 35.6)}^{2} + 0.003 5 {(Y - 4)}^{2}}$ 的变异比较, 其中, 幂律模型有AD_s=0.462, DR模型有AD_s=0.564和AD_MR=0.658。两个模型比较各自的R'(XY)差异不大, 且均控制在Y法的R范围内。

2 结果与讨论

2.1 R'测试条件下的GESD离群检查

数据集变换后需要做单变量广义极值学生化偏差GESD技术检查, 这种检查是一种四分位数回归分析的多离群值测算法。 GESD首先明确疑似离群值数的上限, 通过比较每个数据点标准化残差与预测阈值之间的偏差, 来予以识别异常值。

离群值的检测算法有多种手段和方法, 例如有曼德尔的h和k统计量、数值方法、何克伦(Cochran)和格拉布斯(Grubbs)检验等。因解释离群点的意义经常发生多义性, 且现实情况下数据集相互掩盖的异常值不止一个, 则本工作建议在X法和Y法的离群值检验中, 采用掩蔽现象具有较好抵抗能力的GESD检测技术为宜。

不同于Grubbs和Cochran两端极值剔除的检验, GESD在错误概率0.01的决策准则下能同时识别出多个异常值, 该检查信息量大, 可防止数据被过度甄别处理。

2.2 数据对样本量的功效判断

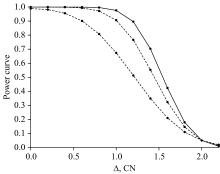
表4中第一阶段的数据对样本量为n=20, 第二阶段的数据对样本量为n=30, 样本量的设计可通过检出功率曲线来判断^[11]。

图4的检出功率曲线表明, 第二阶段的30批次样品量设计具有其合理性(n=30为收益递减的可接受点, 以低成本投入争取DQO优化的高效益)。图中所示, 输入变量的消费者风险0.05, 对称限± 2, 样品设计2和Z(α)=1.645。样本量设计目标90%不应太低, 其中检出功效1-β 承担了接收错误的风险。图中的三条曲线从左至右分别表示n=10(折线)、 n=20(折线)和n=30(实线)的样本量, 并在点(2, 0.05)相交。这些曲线处于柴油45-56(CN)的NIR测试范围, 功效曲线越右移, 越容易接受Δ(绝对差)的等效检验。

	Figure Option View Download New Window
	图4 不同功效曲线下的样本量选择Fig.4 Sample size selection for different power curves

图4的观察时间和成本、输出对异常的响应速度(过程动态)以及对反应不及时的后果, 这些都是考虑采样的实际因素。采样频率过高也会导致连续子群间的自相关性。所以, 应根据两种风险和错误决策成本的可接受水平, 来做权衡。显然, 第一阶段的Δ取n=20功效是勉强的, 而第二阶段共有n=30则大于90%, 说明取Δ的实验失败风险小于10%。

2.3 拟合优度检验

X法和Y法的系统已接受i.i.d状态下正态性和独立性的解消假设, 可不必按数学模型传播法(bottom-up)的思路来评定每个水平的变异。配合休哈特管控图的ACF目测分析[见图5(a)], 本工作更关注式(1)重尾分布修正的二次统计量AD_MR检验[见图5(b)]。

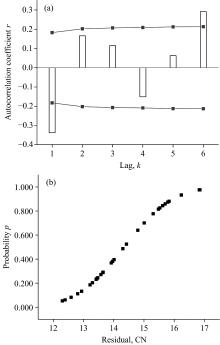	Figure Option View Download New Window
	图5 方法间系列残差的自相关趋势分析 (a): 阶滞后序列的ACF图; (b): AD_MR检查的概率图Fig.5 Autocorrelation trend analysis of series residuals between methods (a): ACF of the lagged sequence; (b): Probability of the AD_MR check

有别于均值分布趋于正态的连续性, 独立性指一个随机变量的发生对另一个随机变量不存在影响, 可利用图5(a)做目测分析。图中6个时滞数值(括号内为各自的上下控制限): -0.337 8(± 0.182 6)、 0.165 7(± 0.202 3)、 0.114 7(± 0.206 8)、 -0.151 0(± 0.208 9)、 0.062 6(± 0.212 5)和0.291 4(± 0.213 1)。这些因受到累积冲击效应的干扰或交互所增加的不稳定性, 非通过校准给予消除, 且任何变换不能形成平稳时序, 导致性能无法确定。

随机过程的数字特征中存在ACF函数, 刻划两个不同时刻之间的线性依从关系。即系列残差t₁和t₂的线性依从仅与(t₂-t₁)有关, ACF为单变量(t₂-t₁)的函数。这种随时间推移呈现一致向下或向上的变异趋势, 解释为变量与自身、或前后数值之间的相关, 在数学上表明各时刻的变量相互独立(依赖于随机变量在时间上分布)。期望时序来自独立白噪声过程、以及随滞后的增加而结果接近于0(以往间隔对当前影响不大)。若协方差不等于0, 可调整样本结果的抽取次数不要过于靠近而产生趋势, 导致残差在时序中产生自相关。

图5的ACF图发现不同滞后阶数出现不一致的现象(期望各时间步骤之间的相关性随时间增加而减少趋于消失)。根据以往判断似乎存在一种趋势, 表明解释变量随着滞后阶数的增加而增大(第一滞后超限)。 ACF的主观目测分析能否确定为平稳无趋势尚待敲定。

为配合ACF的作图分析, 本工作建议直接采用MR逐次差分(递差)消除短期波动的AD_MR检验来发现问题。图5(b)有配合分析AD_MR=0.658, 表明在没有确凿的物理证据下, 可以保留数据对的函数样本集拟合, 断定分布滞后回归模型中相邻观测值的随机扰动得到保障。

AD_MR检验的累积分布函数线性化[见图5(b)], 取决于原假设的统计函数值是否落入α错误率下拒绝域内, 见式(1)。 α阈值来自经验累积分布函数F_n(x)与原假设F₀(x)两者间的差异, 权函数在分布F₀两端取大值。所选分布拟合与非参数阶梯函数之间区域的度量, 视为AD统计量的平方距离。通过递推计算求得分布函数的线性化。根据大量现场数据集的试验而确定的临界分别有0.752(95%概率)和1.032(99%概率)。表4的数据集即利用这种递推来度量随机样本与理论PDF的兼容性, 其统计有AD_s=0.564和AD_MR=0.658, 表明没有理由拒绝系统呈正态、独立和响应适宜的统计假设。

不稳定性是NIR-CN系统测试的常见问题。例如, 部件的老化、数据分辨力、软件程序和环境变量的变化等, 造成任意t时刻数据受到所有随机冲击的累积影响增大。所以, AD_s和AD_MR的拟合优度检验不可忽视。

3 结论

针对预测和依赖变量模型, 其决定系数仅做比较而言, 不能作为模型度量的判断准则。当两个变量均存在误差时, 采用幂律、二阶与斜率函数的拟合需审慎。

DR回归模型同时涉及到X和Y的两者误差[R'(XY)], 能正确发现二维数据集的最佳拟合。 NIR-CN系统所设定的DQO目标是否合理, 非取决于DR模型的决定系数度量, 而是建立在i.i.d随机受控前提条件下。所以说, NIR-CN测试系统的DR建模是通过严谨的CSS偏倚修正和AD拟合优度检验完成的。其中, 为避免两类风险和有限信息可能导致模糊推理的非随机性, 尤其注意ACF的滞后目测和时序的AD_MR递归计算(见图5), 这种AD检查描述了尾部频率阶跃函数权重在累积经验分布下的符合程度。

DR回归模型提出的R'(XY)= $\sqrt[]{0.006 {(X - 35.6)}^{2} + 0.003 5 {(Y - 4)}^{2}}$ , 是一种不确定度已包含在自由度时域范围内的表征评定(见图3), 用以描述CN过程特性服从NIR系统预期内在的DQO控制状态。建议后续的R'(XY)动态监控更多应从主观决策和应用来自主寻找量值溯源, 利用top-down^[12]路线覆盖时间变化中各方变异所带来的效应。

参考文献

文献列表

[1]	Stand ardization Administration of the People's Republic of China(国家标准化管理委员会). GB/T 386—2021 Stand ard Test Method for Cetane Number of Diesel Fuel Oil(GB/T 386 —2021柴油十六烷值测定法), 2021. [本文引用:2]
[2]	WANG Dou-wen, DENG Yun(王斗文, 邓云). Top-Down Uncertainty Evaluation of Quality Control in Inspection and Testing Laboratory(检验检测实验室质量控制技术top-down不确定度评定). Beijing: China Quality and Stand ards Publishing Medica Co. , Ltd. (北京: 中国质检出版社/中国标准出版社), 2017. [本文引用:1]
[3]	Palma C, Morgado V, da Silva R J N B. Talanta, 2019, 192: 278. [本文引用:1]
[4]	Rigo-Bonnin R, Blanco-Font A, Canalias F. Clinical Biochemistry, 2018, 57: 56. [本文引用:1]
[5]	Wang D W, Sun H R, Pan Z Q, et al. Journal of Testing and Evaluation, 2017, 45(2): 703. [本文引用:1]
[6]	Moralles H F, Rebelatto D A N, Sartoris A. Mathematical and Computer Modelling, 2013, 58(9): 1648. [本文引用:1]
[7]	Datsiou K C, Overend M. Structural Safety, 2018, 73: 29. [本文引用:1]
[8]	Jantschi L, Bolboaca S D. Mathematics, 2018, 6(6): 88. [本文引用:1]
[9]	Berlinger M, Kolling S, Schneider J. Glass Structures & Engineering, 2021, 6: 195. [本文引用:1]
[10]	WANG Dou-wen, ZHAO Xue-rong, ZENG Ze, et al(王斗文, 赵雪蓉, 曾泽, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2004, 24(10): 1248. [本文引用:1]
[11]	Everest L, Chen B E, Hay A E, et al. BMC Medical Research Methodology, 2023, 23: 179. [本文引用:1]
[12]	Wang D W, Sun Z J, Zhang W Q, et al. Journal of Testing and Evaluation, 2024, 52(4): 2257. [本文引用:1]

0.0

... 0 引言在柴油CN测试中, NIR系统(常规方法, 以下简称X法)是一种多元过程的关联模型测试, 常被用来替代笨重且昂贵的Waukesha十六烷值机操作(参考方法, 以下简称Y法)^[1] ...

... Y法规定的R^[1](括号内为CN值)有: 40(2 ...

0.0

... 协同试验和能力验证非误差控制的有效方式, 重复性(r)太理想而再现性(R)过于保守, 本工作利用X法系统受控下的室内再现性(intermediate limit, R'), 最大限度覆盖时间和空间的广义重复, 以获得更多信息来推断总体^[2,3,4,5] ...

2019

0.0

2018

0.0

2017

0.0

2013

0.0

... d的受控状态, 本工作利用AD拟合优度的检验^[6,7,8,9], 为解消假设的风险预控、优化组合的有效决策和随机化处理提供了更合理的估计 ...

2018

0.0

... d的受控状态, 本工作利用AD拟合优度的检验^[6,7,8,9], 为解消假设的风险预控、优化组合的有效决策和随机化处理提供了更合理的估计 ...

2018

0.0

... d的受控状态, 本工作利用AD拟合优度的检验^[6,7,8,9], 为解消假设的风险预控、优化组合的有效决策和随机化处理提供了更合理的估计 ...

2021

0.0

... d的受控状态, 本工作利用AD拟合优度的检验^[6,7,8,9], 为解消假设的风险预控、优化组合的有效决策和随机化处理提供了更合理的估计 ...

2004

0.0

... 变换后的数据集必须通过式(1)的AD拟合优度检验, 式(1)中, AD分为AD_s(判断正态性和分辨力)和AD_MR(判断独立性), AD_MR计算有移动极差(MR)^[10], p_i为结果的累积正态概率 ...

2023

0.0

... 2 数据对样本量的功效判断表4中第一阶段的数据对样本量为n=20, 第二阶段的数据对样本量为n=30, 样本量的设计可通过检出功率曲线来判断^[11] ...

2024

0.0

... 建议后续的R'(XY)动态监控更多应从主观决策和应用来自主寻找量值溯源, 利用top-down^[12]路线覆盖时间变化中各方变异所带来的效应 ...