本文在进行下述算法实现之前, 均已经对拉曼光谱数据集进行基线校正和去噪等预处理操作。

1.1.1 常用增强方法

数据增强是机器学习和深度学习中的一个重要技术, 主要通过对原始数据进行一系列的变换和处理, 从而提高训练数据集的多样性和数量, 以提高模型的泛化能力和鲁棒性。 为了比较Voigt函数法与其他方法对光谱数据增强后的效果, 这里选用以下三种常用方法作为对照(由于GAN的原理与此类方法有较大差异, 且实现过程更为复杂, 因此不设为对照方法)。

(1)加噪法: 通过对每条光谱数据添加随机高斯噪声;

(2)线性偏移法^[18]: 该方法的函数表达式如式(1)所示, 偏移量为光谱数据标准差的± 0.1倍, 叠加次数是光谱数据标准差的1± 0.1倍, 斜率则在0.95~1.05之间随机均匀调整。

x'=k* x+α* h+δ-h-α2+b(1)

式(1)中, k为缩放比例, α为倾斜度, δ为倾斜时的偏移, h为步长从0到1之间的向量, b为对偏移结果调整的常数项。 x表示原光谱, x'表示用x生成的光谱。

(3)左右平移法: 通过限定光谱位移波动范围, 随机的左右平移光谱。

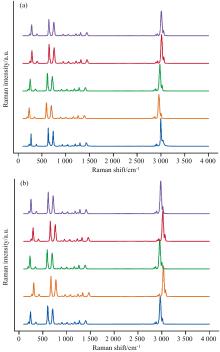
图1(a)为原始光谱样本图, 图1(b)、 (c)和(d)分别为使用加噪、 随机线性偏移和随机左右平移的数据增强方法对该原始光谱扩增五条所生成的增强光谱。 由其定义及光谱样本图可看出, 加噪法仅对光谱基线数据进行扰动, 未能有效增强光谱的谱峰特征, 而偏移法和左右平移法则仅对谱峰特征进行整体变换, 导致生成的谱峰特征之间具有线性相关性。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 原始光谱与常用的增强方法生成的光谱样本图 (a): 原始光谱; (b): 加噪法; (c): 偏移法; (d)左右平移法Fig.1 The original spectrum and the spectrum sample map generated by the commonly used enhancement method (a): Original spectrum; (b): Noise-adding method; (c): Offset method; (d): Left and right translation method

1.1.2 Voigt函数增强方法

Voigt函数主要用于描述由于多普勒展宽和碰撞展宽共同影响下的谱线形状, 从而作为分子光谱线型被广泛应用于光谱分析的研究中。 在数学形式上, Voigt函数定义为高斯函数和洛伦兹函数的卷积^[19], 其数学表达式^[20]如式(2)所示

I(λ)=ICθω2(λ-λC)2+ω2+(1-θ)exp-(λ-λc)22ω2(2)

式(2)中, λ为拉曼位移, I(λ)为λ处的拉曼强度, λ _c、 I_c为谱峰处的位移及其峰值, ω为谱峰的半峰宽, θ为高斯-洛伦兹系数, 该系数的取值范围为(0, 1)。

而对于光谱而言, 通常都具有较多的谱峰, 所以其拟合光谱可以看作是由n个Voigt峰的线性叠加, 其数学表达式如式(3)所示

I(λ)=∑t=1nItθtωt2(λ-λt)2+ωt2+(1-θt)exp-(λ-λt)22ωt2(3)

使用Voigt函数对光谱数据进行拟合的通用算法为: 首先使用寻峰算法提取光谱数据中的每一个谱峰信息。 寻峰算法通过比较数据中每个点与其相邻点的值, 识别出局部极大值, 即可得到谱峰的位置和幅值。 随后, 根据每个谱峰的位置和幅值, 找到峰高一半处的左右边界, 从而精确计算出谱峰的半峰宽。 最后, 利用Voigt函数即可对每个谱峰进行拟合, 将得到的所有拟合峰进行线性叠加, 即可实现对光谱数据进行重构。

考虑到光谱仪本身具有暗噪声, 有些物质的光谱经过基线校正处理后可能会出现倒峰的情况, 对于出现倒峰的光谱, 如果倒峰特征明显, 则要保留作为光谱的特征峰。 因此, 为了提高算法的通用性, 我们对拟合算法进行了改进。 首先, 需要找到光谱的基线位置, 分别计算光谱中最大正峰和最大倒峰到基线位置的幅值, 设定一个比例参数, 该参数与最大正峰的幅值相乘, 得到一个最小阈值(例如, 最大正峰的幅值的20%)。 如若最大倒峰的幅值大于这个最小阈值, 则说明其倒峰特征明显, 需要保留其倒峰信息。 通过这些步骤, 算法能够更准确地处理包含倒峰的光谱数据, 确保在复杂的光谱数据中实现更精确的拟合和重构。

在进行倒峰的峰函数拟合之前, 需要对其进行预处理过程。 首先, 找到光谱的基线高度并将其降至零值, 从而将倒峰转换为负峰。 接着, 复制并翻转数据, 使得负峰变为正峰。 随后利用上述通用拟合算法对基线降为零值的正峰和翻转后的正峰分别进行拟合, 最后对翻转得到的正峰进行逆操作, 并将其与基线降为零值的正峰进行线性叠加, 还原基线高度, 即可得到存在倒峰时的拟合光谱, 图2为存在倒峰时使用Voigt函数进行拉曼光谱拟合的过程图。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Voigt函数的拟合过程图 (a): 寻找到的谱峰; (b): 拟合正峰; (c): 拟合倒峰; (d): 重构的光谱图Fig.2 The fitting process diagram of Voigt function (a): The spectral peak found; (b): Fitting positive peak; (c): Fitting negative peak; (d): Reconstructed spectra

因此, 基于Voigt函数的拉曼光谱增强方法的算法流程图如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
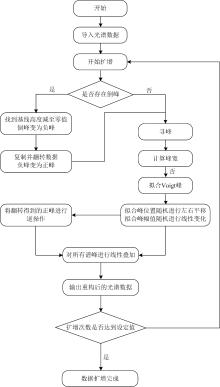	图3 基于Voigt函数的拉曼光谱增强方法的算法流程图Fig.3 The algorithm flow chart of Raman spectroscopy enhancement method based on Voigt function

该算法首先需要判断增强的光谱是否存在倒峰, 若存在, 则使用改进的拟合算法, 若不存在, 则直接使用通用拟合算法。 得到光谱中所有谱峰的拟合峰后, 对每个拟合峰进行数据增强操作。 具体而言, 就是将每个拟合峰当作该光谱的基元, 对其位置给定范围内进行随机左右平移, 同时对其幅值给定范围进行随机线性变换, 然后对光谱中增强后的所有谱峰进行线性叠加, 设置扩增次数, 即可得到增强后的光谱数据。 如图4所示, 该方法对原始光谱数据[图1(a)]进行扩增十条的增强处理后, 获得了具有显著差异性的增强光谱数据, 与加噪法[图1(b)]、 偏移法[图1(c)]和左右平移法[图1(d)]相比, 该算法生成了具有不同峰形、 强度和位移的谱峰特征, 所得的谱峰特征之间具有非线性关系, 有效提升了光谱样本的特征多样性。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Voigt函数增强方法生成的光谱样本图Fig.4 Spectral sample map generated by Voigt function enhancement method

利用增强后的光谱数据, 对K近邻(KNN)、 支持向量机(SVM)和一维卷积神经网络(1D-CNN)三种分类模型进行训练, 并基于训练得到的模型性能来评估增强数据集优劣。 KNN算法是一种简单但有效的监督学习算法, 主要用于分类和回归任务, 在光谱分析中, 通过比较光谱数据点之间的距离来进行分类。 SVM是一种广泛应用于分类和回归分析的监督学习算法。 由于光谱之间存在非线性关系, SVM可以通过使用核函数将数据映射到高维空间, 从而在高维空间中找到一个线性超平面来实现分类^[21]。 采用交叉验证的方法, 找到光谱数据分类最优的核函数为径向基函数(RBF)核

K(xi, x)=exp(-γxi-x‖2)(4)

同时也使用一维卷积神经网络(1D-CNN)对光谱数据进行分类识别, 1D-CNN是卷积神经网络的一种特殊形式, 主要用于处理一维数据, 能够自动的提取序列数据的中的特征, 更好的捕捉序列数据的结构和依赖关系。 本文使用的1D-CNN模型结构由5个卷积层、 5个最大池化层和2个全连接层组成。

1.3.1 增强数据质量评价指标

通过引入结构相似度(SSIM)和PCA总解释方差占比两种评价指标来评价增强数据的质量。

(1) 结构相似度(SSIM)

SSIM本是用于衡量两幅图像相似度的感知指标, 但其核心思想可以推广到一维数据中, 可以从结构上用来衡量原始数据和增强后的数据之间的结构相似度, SSIM的值越接近于1, 说明二者结构上更为相似。 计算公式如式(5)所示

SSIM(x, y)=2μxμy+c1)(2σxy+c2)(μx2+μy2+c1)(σx2+σy2+c2)(5)

式(5)中, μ _x和μ _y代表均值, σ _x和σ _y代表方差, σ _xy代表x和y的协方差, c₁和c₂为常数项。

(2) PCA总解释方差占比

主成分分析(PCA)是一种常用的数据降维技术, 其核心思想是将高维数据投影到低维空间, 同时尽可能保留数据的主要特征。 在PCA中, 解释方差占比用于衡量每个主成分对数据总方差的贡献, 而总解释方差占比是指前k个PCA解释方差占比之和, 用于衡量这k个主成分对数据整体方差的解释能力。 较高的总解释方差占比意味着通过较少的主成分就能解释大部分数据的方差, 从而有效的提取数据的主要特征。 这不仅意味着数据降维过程中的信息损失较少, 还反映了原始数据本身具有较高的质量和丰富的信息含量。 计算公式如式(6)所示

TEVR=∑i=1kλi∑j=1kλj(6)

式(6)中, λ _i表示第i个主成分的特征值, ∑j=1kλ _j表示所有k个主成分特征值之和(即总方差)。

1.3.2 模型效果评价指标

准确率(Acc)是分类问题中最常用的评估指标之一, 用于衡量分类模型中所有预测中正确分类的比例, 正常情况下, 模型的准确率越接近于1, 说明模型的分类效果越好。 计算公式如式(7)所示

Acc(%)=NpNt×100(7)

式(7)中, N_p为正确分类的样本数, N_t为样本总数。

实验所使用的拉曼光谱数据集来源于Wiley Science Solutions网站(Raman Spectral Databases-Wiley Science Solutions)中的公开拉曼光谱数据库的部分拉曼光谱数据库图集, 然后使用图像处理算法对拉曼光谱数据库图集中的拉曼光谱数据进行提取, 其中包含二氯甲烷、 二氯乙烷、 苯酚、 丙酮、 甲苯和二甲苯等65种化合物物质, 共计137条拉曼光谱数据, 以模拟少样本多类别情况下的物质分类。

本文首先采用上述四种数据增强方法对每条拉曼光谱数据扩增十倍, 构建了四组数量为1370条的拉曼光谱增强数据集。 然后对扩增后的数据与其原始数据进行了SSIM和PCA总解释方差占比的质量评价。 分别使用四组光谱增强数据在两种评价方法下的均值代表该组数据的增强质量指标, 以此进行分析比较。

在分类模型测试部分, 考虑到不同类别样本数量不均衡的问题, 我们采用了随机过采样^[22]的方法, 以确保各类别样本数量一致, 从而使得数据分布更加均匀。 然后, 将每个数据集按照80%的比例划分用于训练集, 剩余20%用于验证集。 为了测试增强后的数据是否会对原始数据的分类结果产生影响, 实验将原始数据也用以验证, 并对每条原始数据模拟了实际应用中可能出现的四种异常光谱数据作为测试集, 包括:

(1)由于光谱仪故障或数据采集错误导致的波长范围内数据缺失或不完整;

(2)由于光谱仪老化或偏移导致的光谱数据随机左右平移;

(3)由于光谱仪灵敏度或检测器响应变化引起的光谱幅值波动;

(4)由于样品不纯而出现的不规则尖锐峰。

其中, 异常光谱中的缺失位置、 左右平移的位移、 幅值变换的幅度和产生的不规则尖锐峰均为随机产生。 图5为正常光谱数据与不同情况下的异常光谱数据的对比图, 其中蓝色曲线为原始光谱, 红色曲线为异常光谱。 通过比较异常光谱数据在分类模型中分类的准确率, 旨在验证模型在不同增强方法下的泛化能力, 以期为实际应用提供更可靠的分类性能。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 原始光谱与异常光谱对比图 (a): 缺失数据; (b): 左右平移数据; (c): 幅值变化数据; (d): 异常峰数据Fig.5 Comparison of original spectrum and abnormal spectrum (a): Missing data; (b): Left and right translation data; (c): Amplitude change data; (d): Abnormal peak data

实验创建了Anaconda虚拟环境, 使用Python中的Scikit-learn和Pytorch运算库分别实现KNN、 SVM和1D-CNN模型对四组拉曼光谱增强数据集的训练和分类验证。 在KNN中, 选择最小近邻K=2来对光谱进行分类; 在SVM中, 通过交叉验证法, 寻找到其最优的参数组合为C=10, kernel=“ rbf” ; 而对于1D-CNN, 选择交叉熵损失(Cross-Entropy Loss)作为损失函数, Adam算法作为优化函数, 学习率lr为0.001。 为了更快的实现收敛, 设置批处理大小(Batch Size)为64, 以及训练轮数(Epoch)为10轮。 模型训练完成后, 将生成的异常光谱数据送入训练好的模型进行分类测试, 通过模型分类的准确率高低来评价模型的性能及其泛化能力的大小。 这三种分类模型在训练时均已经经过参数调试和优化, 确保其性能能达到最佳状态。 对每个分类模型进行10次实验, 并记录了验证集分类准确率和原始数据分类准确率的情况, 以验证集和原始数据的准确率均为最大值时确定为最优分类模型。

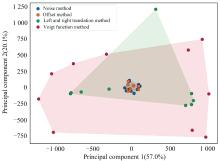
本文对四种不同的数据增强方法在SSIM和PCA总解释方差占比两种评价指标下的表现进行了比较。 根据表1的数据进行分析, 左右平移法和Voigt函数法在两种指标下均表现出较高的有效性, 其SSIM评价值分别为0.849和0.776, PCA总解释方差占比评价值分别为0.857和0.898, 表明这两种方法在保持数据结构相似性方面具有明显优势, 同时在增强数据的信息含量方面也表现出卓越的能力。 相比之下, 加噪法和偏移法在两个评价指标下均表现不佳, 其SSIM评价值分别为0.465和0.547, PCA总解释方差占比评价值分别为0.364和0.412, 表明这两种方法在数据增强效果上存在局限性。 图6展示了对二氯乙烷拉曼光谱数据采用四种不同增强方法后通过PCA降维得到的增强数据分布图, 图中由Voigt函数法增强的样本呈现出更广泛的光谱空间, 表明该方法能有效提升光谱样本分布的多样性。

表1

Table 1

表1(Table 1)

表1 不同数据增强方法生成增强数据集的质量评价 Table 1 Quality evaluation of enhanced data sets generated by different data enhancement methods 评价方法 加噪法 偏移法 左右 平移法 Voigt 函数法 SSIM 0.465 0.547 0.849 0.776 PCA总解释方差占比 0.364 0.412 0.857 0.898

表1 不同数据增强方法生成增强数据集的质量评价 Table 1 Quality evaluation of enhanced data sets generated by different data enhancement methods

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 基于PCA的二氯乙烷拉曼光谱在不同增强方法下的增强数据分布图Fig.6 Distribution of enhanced data of dichloroethane Raman spectra based on PCA under different enhancement methods

图7展示了使用1D-CNN模型对四种增强方法得到的增强数据集进行训练后的最优分类模型的Loss曲线。 其中, 蓝色曲线代表训练损失、 黄色曲线代表验证损失以及绿色曲线代表原始数据进行分类得到的损失。 从图中可以看出, 使用加噪法和偏移法生成的增强数据集进行训练, 模型的分类效果能够迅速达到最佳, 这是由于这两种方法生成的增强数据相对单一, 从而导致模型快速收敛, 未能学习到更多的光谱特征。 使用左右平移法生成的增强数据集训练的模型效果虽然在验证集上表现良好, 但在原始数据中分类效果较差, 得到的原始数据损失较大。 这表明, 左右平移法得到的增强数据可能改变了数据的原始固有分布, 从而影响了模型在原始数据上的表现。 相比之下, 使用Voigt函数生成的增强数据集训练的模型的分类效果表现优秀, 虽然在原始数据分类初期略有波动, 但在经过多轮训练以后也能达到最优效果。

图7

Fig.7

Figure Option ViewDownloadNew Window

图7 不同数据增强方法训练1D-CNN模型时的Loss曲线图 (a): 加噪法+1D-CNN模型Loss曲线; (b): 偏移法+1D-CNN模型Loss曲线; (c): 左右平移法+1D-CNN模型Loss曲线; (d): Voigt函数法+1D-CNN模型Loss曲线Fig.7 Loss curves of 1D-CNN model trained by different data enhancement methods (a): Noise method+1D-CNN model Loss curve; (b): Offset method+1D-CNN model Loss curve; (c): Left and right translation method+1D-CNN model Loss curve; (d): Voigt function method+1D-CNN model Loss curve

由表2数据可以看出, 加噪法、 偏移法和Voigt函数法生成的增强数据所训练的KNN、 SVM和1D-CNN分类模型对验证集和原始数据集分类效果出色, 分类准确率均为100%, 但左右平移法结合三类模型表现欠佳, 在KNN模型中验证集准确率为99.80%, 原始数据集准确率为96.35%。 在SVM模型中效果较差, 验证集准确率为98.75%, 原始数据集准确率为94.89%, 在1D-CNN模型中略有提升, 验证集准确率为100%。 但原始数据集准确率为98.54%, 进一步证明了该方法对原始数据的固有分布改变较大, 对某些光谱特征产生了畸变。

表2

Table 2

表2(Table 2)

表2 验证集和原始数据集在不同数据增强方法所训练的分类模型下的准确率 Table 2 The accuracy of the validation set and the original data set under the classification model trained by different data augmentation methods 分类算法 数据集类型 分类准确率/% 加噪法 偏移法 左右 平移法 Voigt 函数法 KNN 验证集 原始数据集 100 100 100 100 99.80 96.35 100 100 SVM 验证集 原始数据集 100 100 100 100 98.75 94.89 100 100 1D-CNN 验证集 原始数据集 100 100 100 100 100 98.54 100 100

表2 验证集和原始数据集在不同数据增强方法所训练的分类模型下的准确率 Table 2 The accuracy of the validation set and the original data set under the classification model trained by different data augmentation methods

表3和表4分别为不同异常数据集在不同数据增强方法所训练的KNN和SVM最优模型下的分类准确率。 从表中数据可以看出, 加噪法和偏移法在缺失数据、 幅值变化数据和异常峰数据中均保持了很好的准确率, 但在左右平移数据中, 准确率很低, 效果很差。 左右平移法仅仅在左右平移数据中相对于加噪法和偏移法保持较高的准确率, 但在其他三种异常数据集中表现较差。 而Voigt函数法不仅在幅值变换数据和异常峰数据中保持最高的准确率, 并且在缺失数据中表现良好, 在左右平移数据中表现也较为出色。 综合评价来看, 利用Voigt函数法得到的模型性能优于其他方法得到的模型性能。

表3

Table 3

表3(Table 3)

表3 不同异常数据集在不同数据增强方法所训练的KNN模型下的分类准确率 Table 3 The classification accuracy of different abnormal data sets under the KNN model trained by different data enhancement methods 数据集类型 分类准确率/% 加噪法 偏移法 左右平移法 Voigt函数法 缺失数据 81.10 81.02 75.18 78.10 左右平移数据 40.14 41.60 61.31 61.31 幅值变换数据 99.27 99.27 94.89 99.27 异常峰数据 100 100 97.08 100

表3 不同异常数据集在不同数据增强方法所训练的KNN模型下的分类准确率 Table 3 The classification accuracy of different abnormal data sets under the KNN model trained by different data enhancement methods

表4

Table 4

表4(Table 4)

表4 不同异常数据集在不同数据增强方法所训练的SVM模型下的分类准确率 Table 4 The classification accuracy of different abnormal data sets under the SVM model trained by different data enhancement methods 数据集类型 分类准确率/% 加噪法 偏移法 左右平移法 Voigt函数法 缺失数据 79.56 80.29 72.99 75.91 左右平移数据 34.30 34.30 69.34 67.88 幅值变换数据 99.27 99.27 94.16 100 异常峰数据 100 100 97.08 100

表4 不同异常数据集在不同数据增强方法所训练的SVM模型下的分类准确率 Table 4 The classification accuracy of different abnormal data sets under the SVM model trained by different data enhancement methods

表5为不同异常数据集在不同数据增强方法所训练的1D-CNN模型下的分类准确率。 从表中数据可以看出, Voigt函数法在该模型中表现出色, 不仅在幅值变换数据中得到的准确率达到100%, 而且和其他增强方法相比, 缺失数据(82.48%)、 左右平移数据(85.40%)以及异常峰数据(97.08%)均为最优的分类准确率。 证明Voigt函数法更适合作为1D-CNN模型下光谱分类的光谱数据增强方法。

表5

Table 5

表5(Table 5)

表5 不同异常数据集在不同数据增强方法所训练的1D-CNN模型下的分类准确率 Table 5 The classification accuracy of different abnormal data sets under the 1D-CNN model trained by different data enhancement methods 数据集类型 分类准确率/% 加噪法 偏移法 左右平移法 Voigt函数法 缺失数据 78.83 80.29 75.18 82.48 左右平移数据 60.58 56.20 82.48 85.40 幅值变换数据 100 100 98.54 100 异常峰数据 75.91 70.80 90.51 97.08

表5 不同异常数据集在不同数据增强方法所训练的1D-CNN模型下的分类准确率 Table 5 The classification accuracy of different abnormal data sets under the 1D-CNN model trained by different data enhancement methods

综上证明Voigt函数法不仅能够提供丰富的数据变体, 提升光谱样本特征与分布的多样性, 而且有助于模型更好地学习数据的内在结构, 从而在保持对原始数据的最优分类能力的同时, 对异常数据也表现优异, 提高了模型的泛化性能。