基于K-MLE的宽浓度范围气体吸收光谱反演方法研究

引用本文

俞沁怡, 范博强, 尤坤, 何莹, 张世奇, 蔡傲雪, 韩泠然, 张玉钧. 基于K-MLE的宽浓度范围气体吸收光谱反演方法研究[J]. 光谱学与光谱分析, 2025,45(9): 2475-2483.
YU Qin-yi, FAN Bo-qiang, YOU Kun, HE Ying, ZHANG Shi-qi, CAI Ao-xue, HAN Ling-ran, ZHANG Yu-jun. A Study of Gas Absorption Spectral Inversion Method Based on K-MLE With Wide Concentration Range[J]. Spectroscopy and Spectral Analysis, 2025,45(9): 2475-2483.
Doi:10.3964/j.issn.1000-0593(2025)09-2475-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于K-MLE的宽浓度范围气体吸收光谱反演方法研究

俞沁怡^1,², 范博强¹, 尤坤¹, 何莹¹, 张世奇^1,², 蔡傲雪^1,², 韩泠然^1,², 张玉钧^1,^*

1.中国科学院合肥物质科学研究院安徽光学精密机械研究所, 安徽合肥 230031

2.中国科学技术大学, 安徽合肥 230026

*通讯作者 e-mail: yjzhang@aiofm.ac.cn

作者简介: 俞沁怡, 2000年生,中国科学技术大学与中国科学院合肥物质科学研究院联合培养博士研究生 e-mail: qyyu@aiofm.ac.cn

收稿日期: 2024-10-21 修回日期: 2025-04-22 接受日期: 2025-04-22

基金: 国家重点研发计划项目(2023YFC3705402),国家自然科学基金项目(62033012),中国科学院合肥研究院院长基金项目(YZJJ2024QN11)资助

摘要

基于朗伯-比尔定律的气体吸收光谱技术被广泛运用于各类污染气体的排放检测研究中, 然而在进行高浓度气体测量时, 由于设备局限性、气体饱和吸收等因素影响, 光谱吸光度与浓度间出现的非线性偏移将使待测气体浓度的测量结果出现严重偏差。利用待测光谱与标准光谱间的线性信号相关性反映两者浓度间的关系, 提出对差分光密度谱间线性相关系数K值进行极大似然估计(K-MLE)来实现宽浓度范围内的气体浓度反演。基于移动区间法计算了气体吸收波段内不同波长处、不同区间大小内的线性相关系数, 对相关系数集合进行区间估计后分段构建似然函数并求解最佳系数估计值, 能够有效避免因信号扰动等问题引起的测量结果波动, 最终结合浓度阈值与补偿方程实现宽范围内浓度反演。以对二氧化硫(SO₂)气体的浓度检测为例, 对不同浓度气体样品获得的30组光谱信号数据进行处理, 用30组浓度均值的相对误差表征反演方法的准确性, 用浓度测量值的标准差衡量反演方法的稳定性。在相同的低浓度条件下, 宽带法、窄带法和K-MLE法计算得出的反演浓度均值误差分别为6.14%、 22.13%和0.11%, 在保证结果较好稳定性的前提下, K-MLE法实现了最佳测量精度; 在0~508 μL·L^-1的宽浓度范围内, K-MLE法浓度反演结果最大均值误差为0.98%, 最大标准差为1.25, 反演效果明显优于其他两种经典方法。结果表明, K-MLE法提供了一种有效的非线性偏移补偿方法, 能够准确且稳定地实现宽浓度范围内的气体浓度反演。

关键词: 信号相关分析; 极大似然估计; 宽浓度范围; 浓度反演方法

中图分类号:O433.51 文献标志码:A

A Study of Gas Absorption Spectral Inversion Method Based on K-MLE With Wide Concentration Range

YU Qin-yi^1,², FAN Bo-qiang¹, YOU Kun¹, HE Ying¹, ZHANG Shi-qi^1,², CAI Ao-xue^1,², HAN Ling-ran^1,², ZHANG Yu-jun^1,^*

1. Anhui Institute of Optics and Fine Mechanics, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China

2. University of Science and Technology of China, Hefei 230026, China

*Corresponding author

Abstract

The gas absorption spectroscopy technique, based on the Lambert-Beer Law, is extensively employed for the detection of various pollutant gases. However, challenges arise due to the limitations of devices, the saturation absorption of gases, and other interfering factors. When measuring gases at high concentrations, these issues create a nonlinear relationship between absorbance and concentration, resulting in significant deviations in gas detection across a wide concentration range.In this paper, we leverage the linear signal correlation between the measured spectra and reference spectra to reflect the relationship between the concentrations of the two. We propose employing Maximum Likelihood Estimation (MLE) to determine the linear correlation coefficient K between spectra signals, facilitating the inversion of gas concentrationsover a wide concentration range.To determine the linear correlation coefficients across variable spectral intervals in the gas absorption band, we implement a moving internal algorithm with adjustable parameters. The interval-wise statistical inference is carried out on the set of correlation coefficients, and optimal parameter estimators, K-values, are derived by constructing a piecewise likelihood function. This approach effectively mitigates fluctuations in measurement results caused by signal perturbation.Ultimately, gas concentration inversion across a wide concentration range is achieved through a combination of concentration threshold and compensation equation. Using sulfur dioxide (SO₂) gas concentration detection as a case study, we process thirty sets of spectral datasets acquired under each predetermined concentration condition. The accuracy of the concentration inversion methodologywas quantified through the relative error of the mean concentrations calculated from thirty replicate measurements. At the same time,its stability wasevaluatedusing the standard deviation of the concentration values. Under identical low-concentration conditions, the broadband method, narrowband method, and K-MLE algorithm demonstrated mean retrieved concentration errors of 6.14%, 22.13%, and 0.11% respectively. Under the premise of ensuring the stability of the results, the K-MLE algorithm achieved superior measurement accuracy. Furthermore, across a wide concentration range of 0~508 μL·L^-1, the maximum mean error for concentration inversion of the K-MLE method is only 0.98%, with a maximum standard deviation of 1.25, outperforming the other two conventional methods. The results demonstrate that the K-MLE method offers an effective approach for nonlinear offset compensation, enabling accurate and stable gas concentration inversion across a wide range of concentrations.

Keyword: Signal correlation analysis; Maximum likelihood estimation; Wide concentration range; Concentration inversion methodology

文章图片

引言

污染气体的排放与泄漏问题与人类身体健康和自然环境质量息息相关^{[1, 2]}。近年来, 各类光学气体检测技术研究得到了大力发展^[3], 其中, 紫外差分吸收光谱技术(ultraviolet differential absorption spectrum, UV-DOAS)因其可靠性高、精度高、选择性强、抗干扰性强等优点, 成为检测SO₂、 NO₂、 NO、 NH₃等污染气体最常用的技术之一, 具有广泛的应用前景^{[4, 5, 6]}。

朗伯-比尔(Lambert-Beer)定律是各光学气体浓度检测技术的基本原理^[7], 然而实际应用场景并不理想: 光谱仪所配置的滤光片无法完全去除因衍射效应产生的高阶次光^[8]; 气池内可能发生光散射和光化学现象^[9], 或因密度梯度、气流状态不稳定出现待测气体分布不均匀现象; 高浓度气体条件下会发生吸收饱和现象, 杂散光在透射光中占比过高, 造成光谱吸光度与浓度间出现非线性偏移, 导致测量结果难以校准、测量灵敏度和精度降低、浓度测量范围受限等一系列问题^[10]。为避免浓度反演中发生非线性偏移, Zhu等提出可以通过缩短样品池长度或采用稀释法降低光路中的样品浓度^[11]; Tolbin等为确定待测物质的稀释度, 将实际情况中吸光度与浓度的依赖关系近似为分段连续函数, 通过多次求导计算不连续点处的阈值浓度^{[12, 13]}; Abitan等认为朗伯-比尔定律失效的原因是忽略了高光子通量下受激辐射和自发辐射的过程, 提出使用Lambert-W函数描述复杂能级结构的光学介质吸收现象^[14]; Peng等使用多项式拟合法构建反演浓度与标准浓度之间的修正模型, NO气体与SO₂气体的满量程误差分别为2.31%与1.89%^[15]。

光谱信号中携带有物质浓度信息, 对不同浓度条件下测得的光谱信号进行相关分析, 可间接确定浓度值间的关系, 实现气体浓度反演。信号相关分析方法常实践于通信系统、雷达系统中, 用于衡量信号间的相似或相依性^{[16, 17]}。本工作将统计学中的参数估计方法应用于计算最佳线性相关系数K_best。参数估计主要指点估计和区间估计^[18], 其中, 利用区间估计可以在置信区间范围内考虑未知参数的分布和不确定性^[19], 点估计中的极大似然方法是一种概率模型参数估计算法, 指利用已知的样本结果来计算最大概率导致这样结果的参数值^[20]。

为应对基于UV-DOAS技术进行气体浓度检测过程中的非线性偏移, 本工作提出了一种对光谱间线性相关系数进行极大似然估计(maximum likelihood estimation of K, K-MLE)后补偿以实现浓度反演的方法。基于移动区间法计算了光谱信号在不同波段处、不同区间长度内与标准光谱间的线性相关系数K值, 利用统计学中的区间估计及点估计方法, 研究了通过求解似然函数极值点得到最佳估计K值的方法, 最终实现了宽浓度范围内的高精度反演。以浓度范围为0~508 μ L· L^-1的SO₂气体在200~226 nm波段范围内的光谱信号作为研究对象, 在各浓度条件下, K-MLE法与宽带法、窄带法相比, 其反演结果具有良好的精确度和稳定性。

1 方法与原理

1.1 基于DOAS技术的浓度反演原理

当一束波长为λ的单色激光穿过有吸收特性的待测气体时, 其透射光强变化可以使用朗伯-比尔定律来确定, 如式(1)所示。其中, I(λ)是光谱仪所测得的光强, I₀(λ)是光源出射光照射到被测气体的光强, σ(λ)为待测气体在波长λ处的吸收截面, 单位为cm²· molecule^-1, c是待测气体浓度, 单位为molecule· cm^-3, L(cm)是测量光通过的光程。

$I (λ) = I_{0} (λ) \times \exp [- σ (λ) \cdot cL]$ (1)

在DOAS系统中, 常需要考虑如瑞利(Rayleigh)散射和米氏(Mie)散射等对光强造成额外衰减的因素, 因此在式的基础上增加散射衰减因子ε(λ), 如式(2)所示

$I (λ) = I_{0} (λ) \times \exp [- σ (λ) \cdot cL - ε (λ)]$ (2)

基于此定义光密度OD(λ), 如式(3)

$OD (λ) = \ln \frac{I_{0} (λ)}{I (λ)} = σ (λ) \cdot cL + ε (λ)$ (3)

在散射衰减因子ε(λ)存在时, 气体吸收光谱的峰值和基线会因散射背景的叠加而发生显著变化, 因此在进行浓度反演前使用多项式拟合法将ε(λ)去除, 得到差分光密度DOD(λ), 将式(3)修正为式(4)

$DOD (λ) = \ln \frac{I_{0} (λ)}{I (λ)} - ε (λ) = σ (λ) \cdot cL$ (4)

若某气体的吸收波段为[λ_s, λ_e], 在此区间内差分光密度的积分值 $\sum DOD (λ)$ 与浓度的关系如式(5)

$\sum_{λ_{s}}^{λ_{e}} DOD (λ) = cL \cdot \sum_{λ_{s}}^{λ_{e}} σ (λ)$ (5)

相同测量条件下, 若有一对应浓度为c_std的标准光谱I_std(λ), 另有一未知浓度c_u的光谱I_u(λ), 那么这两个光谱之间有如式(6)的线性对应关系, 根据此线性关系可进行浓度反演(比例系数为K_ex)

$\frac{\sum DO D_{u} (λ)}{\sum DO D_{std} (λ)} = \frac{\sum \ln \frac{I_{0} (λ)}{I_{u} (λ)}}{\sum \ln \frac{I_{0} (λ)}{I_{std} (λ)}} = \frac{c_{u}}{c_{std}} = K_{ex}$ (6)

在实际测量中, 造成非线性偏移的原因非常复杂, 难以基于产生原理对Beer-Lambert定律进行修正^[21]。

1.2 光谱间线性相关性研究

假设已知某气体的低浓度c_std对应的差分光密度标准谱DOD_std(λ), 吸收波段范围为[λ_s, λ_e], 在相同环境条件下, 测得未知浓度c_u同一气体的差分光密度谱为DOD_u(λ), 在吸收波段可用DOD_std(λ)近似求得待测浓度的DOD_u(λ), 如式(7)所示

$DO D_{u} (λ) = K \cdot DO D_{std} (λ) + e (λ)$ (7)

式(7)中, e(λ)为误差函数。若在波段[λ _x, λ _y](∈ [λ_s, λ_e])内, 误差信号能量E取得极小值时, 可近似认为标准谱DOD_std(λ)与未知谱DOD_u(λ)之间存在线性相关关系, 线性系数为K

$E = \sum_{λ_{s}}^{λ_{e}} e (λ) = \sum_{λ_{s}}^{λ_{e}} [DO D_{u} (λ) - K \cdot DO D_{std} {(λ)]}^{2}$ (8)

$\frac{\partial E}{\partial K} = 0$ (9)

$K = \frac{\sum_{λ_{x}}^{λ_{y}} [DO D_{std} (λ) \cdot DO D_{u} (λ)]}{\sum_{λ_{x}}^{λ_{y}} [DO D_{std} {(λ)]}^{2}}$ (10)

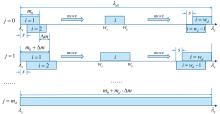
实际测量中, 由于设备稳定性、准确性限制以及各种噪声干扰, 待测浓度c_u差分吸收光谱的不同吸收波段将计算得出不同的K值。本文利用移动区间法遍历待测气体吸收波段内的光谱数据, 区间参数设置与长度、位置计算如式(11)所示, 在总宽度为λ_all的[λ_s, λ_e]吸收波段范围内, 首先设置区间初始长度m₀, 区间长度的增量为Δ m, 第j个区间长度为m, m_d为区间长度可增加次数, 设定区间移动步距为s, w_d为全吸收波段内存在的区间数量, [w_s, w_e]为其中第i个区间的左右边界波长值, 计算不同位置、不同区间长度内相关系数K。式(12)为第i个区间内K_i值计算公式

$\{\begin{array}{l} m_{d} = [\frac{λ_{all} - m_{0}}{Δm}] \\ m = m_{0} + j \cdot Δm, 0 \leq j \leq m_{d} \\ m_{0} + m_{d} \cdot Δm \leq λ_{all} \end{array}$ (11a)

$\{\begin{array}{l} w_{d} = [\frac{λ_{all} - m}{s}] + 1, λ_{all} = λ_{e} - λ_{s} \\ w_{s} = λ_{s} + (i - 1) * s, 1 \leq i \leq w_{d} \\ w_{e} = w_{s} + m - 1 \end{array}$ (11b)

$K_{i} = \frac{\sum_{w_{s}}^{w_{e}} [DO D_{std} (λ) \cdot DO D_{u} (λ)]}{\sum_{w_{s}}^{w_{e}} [DO D_{std} {(λ)]}^{2}}$ (12)

移动区间法的原理如图1所示。

	Figure Option View Download New Window
	图1 移动区间法原理Fig.1 Principle of the moving interval method

1.3 K值数据处理

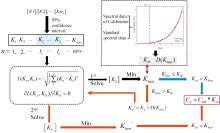
为提高利用K值数据进行线性浓度反演的准确性, 同时扩大该方法适用的浓度范围, 本文提出对不同区间大小内的K_i值数据集合进行处理修正, 最终获得待测浓度反演所需K_ex值的方法, 流程如图2所示, 分为四步: (1)筛选出待测谱中各不同区间长度下的K值集合[K1], [K2], …, [Kj], …, [Km_d]中95%置信区间内的所有元素K_n(n=1, 2, …, new), 组成新集合[K_new]; (2)基于极大似然估计法针对集合[K_new]中的元素构建似然函数L(K_n, K_b), 如式(13)所示, 该函数反映区间[ $K_{l_{s}}$ , $K_{l_{e}}$ ]内K_n值与理想估计值K_b之间的逼近程度, 分段构建似然函数有利于最小化数据波动对结果的干扰, 求解方程∂ L(K_n, K_b)/∂ K_b=0, 得到最佳估计值集合[K_b]; (3)将[K_b]中的所有元素重新代入似然函数L(K_n, K_b), 使此函数值最大的K_b定义为K_best; (4)比较线性相关系数阈值K_th与K_best, 决定是否对[K_new]内元素进行修正补偿, 若K_best≤ K_th, 则K_ex=K_best, 若K_best> K_th, 则对[K_new]中的元素进行修正后重复步骤(3), 最终实现浓度反演。

$L (K_{n}, K_{b}) = - \sqrt[]{\frac{1}{l} \sum_{l_{s}}^{l_{e}} (K_{n} - K_{b})^{2}}$ (13)

在进行待测浓度反演前, 需利用标准谱与标定谱确定线性相关系数阈值K_th与修正方程D(K_best)。其中, K_th与阈值浓度c_th相关, 定义为K_th=c_th/c_std; 修正方程D(K_best)表示初步计算得出的线性系数最佳估计值K_best与准确系数值K_ex之间的偏差程度, 基于前文提到的K值计算与处理方法计算不同浓度条件的标定谱对应的K_best, 当K_best> K_th时, 拟合K_best与K_ex-K_best间的关系, 定义为D(K_best)。

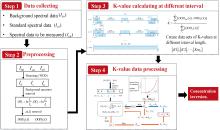
	Figure Option View Download New Window
	图2 K-MLE法中数据处理流程图Fig.2 The process of data processing in K-MLE

综上, 提出的K-MLE法流程如图3所示: 首先对采集到的背景光谱、标准光谱、标定光谱以及待测光谱数据进行小波去噪以提高信噪比, 并进行去除背景谱、去除ε(λ)等预处理, 基于移动区间法计算待测谱吸收波段内不同区间及位置处的线性相关系数K, 对K值进行多级处理并补偿后实现待测气体浓度反演。

	Figure Option View Download New Window
	图3 K-MLE法流程图Fig.3 The process of K-MLE

2 实验结果与讨论

2.1 实验装置

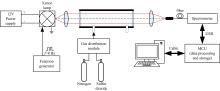
基于差分吸收光谱的SO₂气体浓度检测系统如图4所示, 该装置主要由光学系统、电学系统和气路系统组成。工作波段范围为185~2 000 nm的氙灯(Hamamatsu, L9456-01)发出的光束经焦距为2 cm的透镜准直为平行光, 通过光程长约20 cm、体积为约90 mL的样品池, 样品池的两端有进气口和出气口, 以保证待测气体快速流通。穿过样品池的透射光通过透镜聚光到光纤中, 耦合到分辨率为1.5 nm 的紫外光谱仪(Ocean Optics USB4000), 再连接到MCU (FriendlyARM, Smart210)中进行数据处理和存储。系统使用基于质量流量计(Sevenstar Electronics, CS100)的气体配比模块, 相对偏差为1%。实验中不同浓度的SO₂气体由南京特气有限公司出售的SO₂(508 μ L· L^-1)和N₂(99.9%)标准气瓶提供, 不确定度2%, 气体流量控制在1 L· min^-1。

	Figure Option View Download New Window
	图4 基于UV-DOAS技术的气体检测系统Fig.4 Gas detection system based on UV-DOAS technology

整个实验在室温(25 ℃)和一个大气压(101.3 kPa)条件下进行。光源预热5 min后开始实验, 向气池内充入氮气, 吹扫气池并采集信号作为背景谱, 随后向气池内通入多种体积占比不同的SO₂气体, 每种浓度的光谱信号采集30次, 相邻两次采集间隔1 min, 每次保存光谱数据时通气状态保持10 min以上, 以保证气体已完全充满气池且形成稳定状态。

2.2 光谱数据采集与预处理

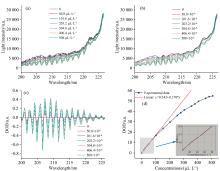
基于气体检测系统采集不同浓度气体的原始光谱信号, 如图5(a)所示。对所有原始光谱进行相同参数(heursure阈值法、软阈值函数、 3层分解层数、 sym8小波基)的小波滤噪(Wavelet domain denoising, WDD)后光谱信号如图5(b)所示, 其中508 μ L· L^-1浓度条件下的光谱信噪比(SNR)在滤波后提高了14.96%; 基于前文所提到的差分吸收光谱原理, 得到SO₂在200~226 nm 波段相应浓度下的差分光密度DOD(λ), 如图5(c)所示; 计算DOD(λ)在整个吸收波段内的积分值, 结果与对应的标准气体浓度的关系如图5(d)所示: 当气体浓度低于90 μ L· L^-1时, DOD(λ)积分值与浓度呈良好的线性关系(线性斜率=0.170, R²=0.996), 符合线性测量需求, 将90 μ L· L^-1确认为线性阈值浓度c_th; 随着气体浓度升高, 吸光度增长速率减缓, 出现吸收饱和现象, DOD(λ)积分结果与浓度之间的线性关系逐渐偏离。

Figure Option
View Download New Window

图5 光谱数据预处理
(a): 不同浓度气体测得的原始光谱信号; (b): 小波滤波后的光谱信号; (c): 不同浓度气体的差分光密度谱; (d): 差分光密度积分值与浓度间的非线性偏移Fig.5 Spectral data preprocessing
(a): Raw spectral signals measured at different concentrations; (b): Spectral signal after wavelet filtering; (c): Differential optical density at different concentrations; (d): Nonlinear relationship between integral value of differential optical density and concentrations

2.3 K值计算分析

为确定待测气体的光谱数据在不同波段区间中的线性偏离程度, 将采集的30组浓度为40.64 μ L· L^-1的光谱信号滤波后进行平均作为标准光谱, 即c_std=40.64 μ L· L^-1, 线性相关系数阈值K_th=2.2, 对3种浓度条件下(50.8、 203.2和508 μ L· L^-1)的差分吸收光谱数据进行线性相关系数计算分析。基于前文提出的移动区间法计算K值, 在200~226 nm 的吸收波段中选取大小分别为1、 2、 5、 10 nm的区间, 区间移动步距s均设置为0.5 nm, 在区间移动过程中计算每个区间的K_i值。图6为不同浓度的SO₂吸收光谱数据在不同波长处、不同大小区间中K_i值与准确值K_ex(K_ex=c_u/c_std)之间的相对误差, 横坐标代表区间中心波长, 图中标注了K_i值在± 5%误差范围及95%置信区间内的分布情况。

	Figure Option View Download New Window
	图6 不同浓度梯度下的K值分布 (a): c=50.8 μ L· L^-1; (b): c=203.2 μ L· L^-1; (c): c=508 μ L· L^-1Fig.6 K-values at different concentrations (a): c=50.8 μ L· L^-1; (b): c=203.2 μ L· L^-1; (c): c=508 μ L· L^-1

由图6可知, 相同浓度下K_i值的相对误差在不同波段范围内区别较大, 这表明气体在不同波段内的吸收特性与浓度间存在非线性关系。 50.8 μ L· L^-1的浓度条件下, 64.5%的K_i值分布在± 5%的误差区间内, 区间长度较短时K_i值波动较大, 在所选吸收波段内, 1 nm区间对应的K_i值标准差(standard deviation, SD)为0.183, 均值误差为6.4%, 而10 nm区间内K_i值分布更集中, SD为0.019, 均值误差为1.6%, 结果表明当气体浓度处于线性吸收范围内时, 宽区间能够更精确且稳定地进行低浓度反演。气体浓度升高后, K_i值分布逐渐呈现整体远离K_ex的趋势, 分布在± 5%的误差区间内的K_i逐渐减少: 508 μ L· L^-1浓度条件下, 1 nm区间K_i值SD为3.47, 均值误差为-39.15%, 10 nm区间的K_i值SD为0.93, 均值误差为-33.25%, 宽区间浓度反演结果虽然波动较小, 但均值误差大, 无法满足浓度反演需求。

对不同浓度下四种区间长度计算得出的K_i值集合进行95%置信区间计算, 结果如表1所示。浓度升高后出现非线性偏移现象, 区间中点值与准确值K_ex间的误差增大, 区间宽度增大代表数据不确定性增加, 因此需对置信区间内的K_i值进行进一步计算筛选, 并对结果进行非线性修正, 最终实现浓度反演。

表1 K值的95%置信区间 Table 1 95% confidence interval of K-value

2.4 K-MLE浓度反演

将实验收集的8种不同浓度条件下30组光谱数据进行预处理后, 根据阈值浓度c_th将其分类为低浓度与饱和吸收浓度。利用宽波段(200~226 nm)、窄波段(218~220 nm)的差分吸收谱与标准谱之间的线性相关系数、以及K-MLE法对低浓度(25.4和50.8 μ L· L^-1)下的光谱数据进行浓度反演, 取每个浓度下获得的30组浓度均值(Mean)作为当前测量浓度值, 以浓度均值的相对误差(mean relative error)表征该反演方法的准确性, 利用SD衡量30组浓度测量值离散程度, 来评价该反演方法的稳定性。选取最小区间长度为1 nm, 区间长度增量为0.5 nm, 移动步距为0.5 nm。

此三种反演方法对低浓度待测气体的浓度反演结果如图7所示: 气体浓度为25.4 μ L· L^-1时, 气体对光强吸收较弱且光谱信号不稳定, 宽带法、窄带法和K-MLE法计算得出的反演浓度均值误差分别为6.14%、 22.13%和0.11%, SD值分别为0.75、 5.76和2.93, 宽带法的测量精度优于窄带法, 窄带法测量结果误差最大且波动最大, K-MLE法的测量精度和稳定性表现良好。当气体浓度增加到50.8 μ L· L^-1时, 宽带法的测量结果均值误差和SD值最低, 分别为0.67%和0.98, 这表明宽带法可以稳定地进行低浓度反演, K-MLE法的结果均差为0.79%, SD为1.11, 表现稍差于宽带法。当气体浓度在线性吸收范围内时, 宽带法和K-MLE法能够相当准确、稳定地进行浓度反演; 而窄带法由于选取的波段短, 参与计算的光谱信号较少, 极易受到信号波动的影响, 稳定性非常差, 不能有效地进行浓度反演。

	Figure Option View Download New Window
	图7 低浓度条件下三种方法反演结果 (a): c=25.4 μ L· L^-1; (b): c=50.8 μ L· L^-1Fig.7 Inversion results of three methods at low concentration (a): c=25.4 μ L· L^-1; (b): c=50.8 μ L· L^-1

待测气体浓度升高至饱和吸收范围内, 必须对宽带法和K-MLE法进行补偿, 宽带法的二次多项式补偿方程为c₂=0.005 8× $c_{1}^{2}$ -0.166 8× c₁+67.518 7, 拟合均方根误差(root mean square error, RMSE)为6.177 1, 其中c₁为根据待测谱与标准谱间线性相关系数得出的初始浓度值, c₂为修正后的测量浓度; K-MLE法中K值修正方程为D(K_best)=0.051× exp(0.590 2× K_best), RMSE为0.080 2。利用两种方法对6种浓度条件下的光谱信号在非线性补偿前后的浓度反演结果如表2所示: 未进行非线性补偿前, 高浓度环境下严重的非线性偏移导致两种方法产生非常大的反演结果偏差, 且反演结果均值误差随着浓度升高而增大。气体浓度值为508 μ L· L^-1时, 宽带法达到最大均值误差为43.00%, K-MLE法的均值误差为38.40%。根据补偿方程对两种方法进行修正后, 101.6~508 μ L· L^-1的浓度范围内, 宽带法的均值误差最大为3.50%, K-MLE法的均值误差低于1%, 最小误差为0.25%, 且反演稳定性优于宽带法。结果表明, 在宽范围的气体浓度反演过程中, K-MLE法在低浓度情况下能够保证良好的反演精度, 在出现非线性偏移的高浓度情况下, 相较于常规的反演方法, K-MLE法能够准确且稳定地进行浓度反演。

表2 非线性补偿的浓度反演方法对比 Table 2 Comparison of concentration inversion methods with nonlinearly compensated

3 结论

基于朗伯-比尔定律的气体浓度反演方法由于实际测量中无法避免的限制因素, 在进行宽范围、高浓度的气体测量过程中, 待测气体吸光度积分与浓度间出现非线性偏移现象, 导致测量结果严重偏离实际浓度值。基于UV-DOAS的气体浓度检测系统, 本文提出了一种应用在宽浓度范围内的非线性吸收光谱反演方法, 利用待测气体差分光密度谱与标准谱之间的线性相关系数K值来反映待测浓度与已知标准浓度之间的关系, 对移动区间法得到吸收波段不同波长处、不同区间大小内K值进行分析, 基于置信区间估计提高K-MLE方法的抗干扰性, 构建线性关系系数的似然方程并求解极大值点, 研究了一种有效的针对最佳估计值K_best的计算补偿方法。相较于宽带法、窄带法, K-MLE法精确且稳定地实现了0~508 μ L· L^-1范围内SO₂气体浓度反演, 最大均值误差为0.98%, 最大标准差为1.25。结果表明, K-MLE法实现了低浓度气体测量中0.11%的测量精度, 同时提出了高浓度情况下一种有效的非线性补偿方法, 为宽浓度范围的气体提供了一种普遍适用的浓度反演方法。

参考文献

文献列表

[1]	Tan H Y, Chen Y M, Mao F Y, et al. International Journal of Digital Earth, 2024, 17(1): 1. [本文引用:1]
[2]	Chen C, Ren Q, Wang Y Z. Applied Spectroscopy Reviews, 2019, 54(5): 425. [本文引用:1]
[3]	Kwasny M, Bombalska A. Sensors, 2023, 23(5): 2834. [本文引用:1]
[4]	ZHANG Zhi-dong, XIE Pin-hua, LI Ang, et al(张之栋, 谢品华, 李昂, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(5): 1651. [本文引用:1]
[5]	Zhu R, Gao J, Li M, et al. Sensors and Actuators B: Chemical, 2023, 394: 134440. [本文引用:1]
[6]	You R X, Kang H, Zhang X, et al. International Journal of Hydrogen Energy, 2024, 86: 14. [本文引用:1]
[7]	Swinehart D F. Journal of Chemical Education, 1962, 39(7): 333. [本文引用:1]
[8]	Offersgaard J F, Öjelund H. Applied Spectroscopy, 2002, 56(4): 469. [本文引用:1]
[9]	Li L, Peng Y, Li Y, et al. Analytica Chimica Acta, 2019, 1087: 20. [本文引用:1]
[10]	De Boni L, Andrade A A, Correa D S, et al. The Journal of Physical Chemistry B, 2004, 108(17): 5221. [本文引用:1]
[11]	Zhu C, Griffiths P R. Applied Spectroscopy, 1998, 52(11): 1403. [本文引用:1]
[12]	Tolbin A Y, Pushkarev V E, Tomilova L G, et al. Physical Chemistry Chemical Physics, 2017, 19(20): 12953. [本文引用:1]
[13]	Tolbin A Y, Pushkarev V E, Tomilova L G, et al. Chemical Physics Letters, 2018, 706: 520. [本文引用:1]
[14]	Abitan H, Bohr H, Buchhave P. Applied Optics, 2008, 47(29): 5354. [本文引用:1]
[15]	Peng B, Tang Z, Xian S J, et al. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2024, 315: 124267. [本文引用:1]
[16]	Pallotta L, Giunta G. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(3): 2568. [本文引用:1]
[17]	ZHAO Guang-zhou(赵光宙). Signal Analysis and Processing(信号分析与处理). Beijing: Machinery Industry Press(北京: 机械工业出版社), 2016. 72. [本文引用:1]
[18]	Wasserman L. All of Statistics: A Concise Course in Statistical Inference, New York: Springer, 2004, 119. [本文引用:1]
[19]	Krishnamoorthy K, Waguespack D, Hoang-Nguyen-Thuy N. Journal of Applied Statistics, 2020, 47(1): 160. [本文引用:1]
[20]	Hu X M. Journal of Systems Science and Complexity, 2014, 27(2): 350. [本文引用:1]
[21]	Mäntele W, Deniz E. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2017, 173: 965. [本文引用:1]

2024

0.0

... 0 引言污染气体的排放与泄漏问题与人类身体健康和自然环境质量息息相关^[1,2] ...

2019

0.0

... 0 引言污染气体的排放与泄漏问题与人类身体健康和自然环境质量息息相关^[1,2] ...

2023

0.0

... 近年来, 各类光学气体检测技术研究得到了大力发展^[3], 其中, 紫外差分吸收光谱技术(ultraviolet differential absorption spectrum, UV-DOAS)因其可靠性高、精度高、选择性强、抗干扰性强等优点, 成为检测SO₂、 NO₂、 NO、 NH₃等污染气体最常用的技术之一, 具有广泛的应用前景^[4,5,6] ...

2023

0.0

2023

0.0

2024

0.0

1962

0.0

... 朗伯-比尔(Lambert-Beer)定律是各光学气体浓度检测技术的基本原理^[7], 然而实际应用场景并不理想: 光谱仪所配置的滤光片无法完全去除因衍射效应产生的高阶次光^[8] ...

2002

0.0

2019

0.0

... 气池内可能发生光散射和光化学现象^[9], 或因密度梯度、气流状态不稳定出现待测气体分布不均匀现象 ...

2004

0.0

... 高浓度气体条件下会发生吸收饱和现象, 杂散光在透射光中占比过高, 造成光谱吸光度与浓度间出现非线性偏移, 导致测量结果难以校准、测量灵敏度和精度降低、浓度测量范围受限等一系列问题^[10] ...

1998

0.0

... 为避免浓度反演中发生非线性偏移, Zhu等提出可以通过缩短样品池长度或采用稀释法降低光路中的样品浓度^[11] ...

2017

0.0

... Tolbin等为确定待测物质的稀释度, 将实际情况中吸光度与浓度的依赖关系近似为分段连续函数, 通过多次求导计算不连续点处的阈值浓度^[12,13] ...

2018

0.0

... Tolbin等为确定待测物质的稀释度, 将实际情况中吸光度与浓度的依赖关系近似为分段连续函数, 通过多次求导计算不连续点处的阈值浓度^[12,13] ...

2008

0.0

... Abitan等认为朗伯-比尔定律失效的原因是忽略了高光子通量下受激辐射和自发辐射的过程, 提出使用Lambert-W函数描述复杂能级结构的光学介质吸收现象^[14] ...

2024

0.0

... 89%^[15] ...

2022

0.0

... 信号相关分析方法常实践于通信系统、雷达系统中, 用于衡量信号间的相似或相依性^[16,17] ...

2016

0.0

... 信号相关分析方法常实践于通信系统、雷达系统中, 用于衡量信号间的相似或相依性^[16,17] ...

2004

0.0

... 参数估计主要指点估计和区间估计^[18], 其中, 利用区间估计可以在置信区间范围内考虑未知参数的分布和不确定性^[19], 点估计中的极大似然方法是一种概率模型参数估计算法, 指利用已知的样本结果来计算最大概率导致这样结果的参数值^[20] ...

2020

0.0

2014

0.0

2017

0.0

... 在实际测量中, 造成非线性偏移的原因非常复杂, 难以基于产生原理对Beer-Lambert定律进行修正^[21] ...