引用本文
范炳瑞, 翟爱平, 王东, 梁婷, 张根伟, 曹树亚. 基于改进高阶残差网络的中红外危化品混合光谱识别研究[J]. 光谱学与光谱分析, 2025,45(9): 2459-2466.
FAN Bing-rui, ZHAI Ai-ping, WANG Dong, LIANG Ting, ZHANG Gen-wei, CAO Shu-ya. Research on the Recognition of Mixed Mid-Infrared Spectra of Hazardous Chemicals Based on an Improved High-Order Residual Network[J]. Spectroscopy and Spectral Analysis, 2025,45(9): 2459-2466.
Doi:10.3964/j.issn.1000-0593(2025)09-2459-08  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于改进高阶残差网络的中红外危化品混合光谱识别研究
范炳瑞1,2, 翟爱平1, 王东1, 梁婷3, 张根伟2,*, 曹树亚2,*
1.太原理工大学物理与光电工程学院, 山西 太原 030024
2.核生化灾害防护化学全国重点实验室, 北京 102205
3.陆军防化学院, 北京 102205
*通讯作者 e-mail: zhgw1984@163.com; caoshuya@skinbcpc.cn

作者简介: 范炳瑞, 1999年生,太原理工大学物理与光电工程学院硕士研究生 e-mail: fabr1999@163.com

收稿日期: 2024-12-05 修回日期: 2025-05-02 接受日期: 2025-05-02
基金: 山西省基础研究计划项目(20210302123195)资助
摘要

在化学工业快速发展的背景下, 大量危险化学品的生产与使用带来了环境风险, 也对人类健康带来了潜在威胁。 因此, 亟需开发高效的监测与识别手段以应对这一挑战。 中红外光谱技术凭借其独特的分子“指纹”识别能力和高灵敏性, 已广泛应用于危险化学品的识别分析。 同时, 近年来深度学习在特征提取和目标检测领域的显著突破, 为解决复杂数据分析问题提供了新思路。 为满足在复杂背景下对危险化学品进行精准识别的需求, 提出了一种结合深度可分离卷积与高阶残差网络的模型(DSC-HORN), 以进一步提升中红外复杂光谱数据的特征提取效率和识别精度。 DSC-HORN模型通过深度可分离卷积技术, 将标准卷积分解为深度卷积和逐点卷积, 从而将参数量和计算复杂度减少了约65.89%。 这一优化使DSC-HORN模型的运行速度较一维卷积神经网络提升约4倍, 显著降低了内垫消耗, 使其在资源受限环境中表现出更高的适应性。 在实验方面, 本研究采集了10%浓度的DMMP溶液在11类地物背景下的中红外混合光谱数据。 经过数据预处理剔除异常样本后, 最终得到528组有效光谱数据用于模型构建。 为了确保不同标签样本在各子集中保持均衡分布, 并真实反映数据的整体分布特征, 采用分层随机抽样方法对数据集进行划分, 以6:1:3的比例分为训练集、 验证集和测试集。 实验结果显示, DSC-HORN模型在识别效率和准确率方面相较现有模型表现出显著优势。 与传统模型(如K-最邻近、 随机森林、 鲁棒众数回归稀疏非负矩阵分解和反向传播神经网络)以及深度学习模型(如一维卷积神经网络)相比, DSC-HORN模型的识别准确率达到96.84%, 较上述模型分别提高了5.7%、 13.93%、 5.07%、 10.76%和6.33%, 这一性能提升归因于深度可分离卷积的参数优化和高阶残差连接的高效特征提取能力。 结果进一步表明, DSC-HORN模型不仅是一种高效准确的中红外危化品识别模型, 还为危险化学品的实时监测与精准识别提供了新的技术路径。 此外, 基于改进高阶残差网络的中红外危化品识别技术, 有望进一步推动中红外光谱技术在复杂场景中的广泛应用。

关键词: 危险化学品监测; 光谱识别; 中红外光谱; 深度可分离卷积; 高阶残差网络
中图分类号:O433.4 文献标志码:A
Research on the Recognition of Mixed Mid-Infrared Spectra of Hazardous Chemicals Based on an Improved High-Order Residual Network
FAN Bing-rui1,2, ZHAI Ai-ping1, WANG Dong1, LIANG Ting3, ZHANG Gen-wei2,*, CAO Shu-ya2,*
1. College of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan 030024, China
2. National Key Laboratory of Nuclear, Biological and Chemical Hazard Protection, Beijing 102205, China
3. Institute of Chemical Defense, Beijing 102205, China
*Corresponding authors
Abstract

Amid the rapid development of the chemical industry, the large-scale production and use of hazardous chemicals have brought significant environmental risks and potential threats to human health. Consequently, there is an urgent need to develop efficient monitoring and identification methods to address these challenges. Mid-infrared (MIR) spectroscopy, characterized by its unique molecular “fingerprint” recognition capability and high sensitivity, has been widely applied in the identification and analysis of hazardous chemicals. Meanwhile, recent breakthroughs in deep learning, particularly in feature extraction and object detection, have provided novel solutions for addressing complex data analysis problems. To meet the need for precise identification of hazardous chemicals under complex background conditions, this study proposes a novel model that combines Depthwise Separable Convolution (DSC) and a High-Order Residual Network (HORN), referred to as DSC-HORN. This model is designed to enhance further the efficiency of feature extraction and the accuracy of recognition for complex MIR spectral data. By leveraging depthwise separable convolution, the DSC-HORN model decomposes standard convolutions into depthwise and pointwise convolutions, resulting in a reduction of approximately 65.89% in parameter count and computational complexity. This optimization increases the operational speed of the DSC-HORN model by approximately four times compared to traditional one-dimensional convolutional neural networks (1D-CNNs), while significantly reducing memory consumption and enhancing its adaptability in resource-constrained environments. For the experiments, this study collected MIR spectral data of a 10% DMMP solution mixed with 11 types of background materials. After data preprocessing and removal of outlier samples, a total of 528 valid spectral datasets were obtained for model construction. To ensure balanced distribution of different labeled samples across subsets and to accurately reflect the overall data characteristics, the dataset was divided into training, validation, and testing sets using a stratified random sampling method, with a 6:1:3 ratio for training, validation, and testing, respectively. The experimental results demonstrated that the DSC-HORN model exhibits significant advantages in recognition efficiency and accuracy compared to existing models. Compared to traditional models such as K-Nearest Neighbors(KNN), Random Forest(RF), Robust Mode Regression Sparse Non-negative Matrix Factorization(MR-NMF), and Backpropagation Neural Networks(BP), as well as deep learning models like1D-Convolutional Neural Network(1D-CNN), the DSC-HORN model achieved a recognition accuracy of 96.84%. This represents improvements of 5.7%, 13.93%, 5.07%, 10.76%, and 6.33%, respectively, over the models above. These performance enhancements can be attributed to the parameter optimization achieved through depthwise separable convolution and the efficient feature extraction enabled by high-order residual connections. The results further confirm that the DSC-HORN model is not only an efficient and accurate MIR hazardous chemical recognition model but also provides a novel technical pathway for real-time monitoring and precise identification of hazardous chemicals. Additionally, the MIR recognition technology, based on the improved high-order residual network, has great potential to promote further the widespread application of MIR spectroscopy in complex scenarios.

Keyword: Hazardous chemical monitoring; Spectral recognition; Mid-infrared spectroscopy; Depthwise separable convolution; High-order residual network
引言

随着社会经济的快速发展和工业化进程的不断加速, 化学工业在国民经济中的地位和作用愈发重要, 但在其生产过程中大量使用的危险化学品也带来了潜在的环境风险和对人类健康的严重威胁。 一旦这些危险化学品管理不当, 可能引发严重的环境污染或安全事故, 造成不可挽回的损失。 近年来的一系列重大化学事故凸显了危险化学品识别与安全处理的重要性。 例如, 2015年天津港爆炸事故导致了严重的环境污染和人员伤亡; 2019年山东致爆物品生产企业爆炸事故以及江苏化工厂爆炸事故亦造成了巨大损失。 因此, 对危险化学品的高效监测和安全控制已成为社会关注的重点。 在这一背景下, 红外光谱技术由于具有绿色高效、 可实时在线分析等特点, 已经成为发展最快和最引人瞩目的一门独立的分析技术[1]。 特别是中红外光谱技术, 凭借分子振动产生的吸收峰, 可以提供物质的特定化学“ 指纹” , 从而实现对复杂样本的精准识别。 这一技术不仅在化学分析[2]中被广泛应用, 还在食品安全[3]、 生物医学[4]、 环境监测[5]等领域展现出巨大潜力。

近年来人们开始探索基于近红外光谱和中红外光谱分析识别化学品, 郭腾霄等利用支持向量机建立危险化学品红外遥测光谱的鉴别模型, 基于40个训练样本建立的模型对267个测试样本的鉴别正确率达到93.6%[6]。 冷思雨等利用改进的U-Net++网络结合近红外光谱技术, 提出了一种羊毛含量的快速定性分析方法, 预测准确率达到了93.59%[7]。 现有化学品光谱研究多集中于近红外区域, 而中红外领域的危化品研究相对较少。 中红外光谱特别擅长处理复杂分子结构的物质, 如有机化合物和多组分混合物, 能够通过特定波段的吸收峰识别分子特征。 尽管中红外光谱技术具备显著优势, 在实际混合光谱的识别应用中仍然面临一些挑战。 复杂背景环境(如植被、 土壤及水体)中的干扰信号, 会导致光谱数据的噪声增多, 影响分析的精度。 传统的光谱分析方法在处理这些问题时有一定成效[8], 但在多组分混合物的高维光谱数据处理中, 其提取特征的能力有限。 这些问题严重影响了该技术在复杂背景条件下的广泛应用。

针对这些问题, 研究者们开始探索将红外光谱技术与深度学习相结合, 以进一步提升光谱分析的效率和准确性。 深度学习具有强大的自动特征学习能力和高度鲁棒性, 已经广泛应用于图像处理[9]、 自然语言处理[10]、 生物信息学[11]、 工业自动化控制[12]等领域。 在此, 提出一种结合深度可分离卷积[13]与高阶残差连接的网络结构, 即深度可分离卷积高阶残差网络模型(depthwise separable convolution-high-order residual network, DSC-HORN)。 该模型在处理复杂光谱数据时表现出优越的性能, 尤其适用于复杂环境条件下的中红外光谱分析。

1 方法原理
1.1 DSC-HORN模型设计与架构

对于传统的深度学习算法模型, 随着网络的加深, 模型的准确率往往趋于饱和甚至下降。 为解决这一问题, 同时提高复杂数据模式下的特征提取效率, 本工作提出了DSC-HORN网络模型。 其通过深度可分离卷积将标准卷积分解为深度卷积和逐点卷积, 大幅减少参数数量和计算复杂度, 显著提高计算效率。 同时, 高阶残差连接通过多层残差路径整合深层特征, 增强信息流动与特征复用能力, 从而有效缓解梯度消失的问题, 提升网络的学习能力与泛化性能。

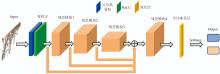
图1展示了DSC-HORN的拓扑结构, 该模型由输入层、 卷积层、 四个残差模块、 全局平均池化层和输出层组成。 输入层明确定义了网络输入数据的形状与维度, 确保数据流能够与网络结构无缝对接, 并高效传递至后续计算模块。 初始卷积层的功能在于提取基础特征并调整通道数, 为后续残差模块的特征处理提供适配的输入。 模型中橙色标识的部分为残差模块, 这种设计通过逐步降低空间分辨率与调整通道数, 实现了多层次特征的分级提取。 全局平均池化层的核心作用在于对每个通道的特征图进行全局均值计算, 生成一个表征该通道整体特征的单一数值。 最终, 输出层通过预测类别的概率分布, 精确完成目标类别的识别任务。

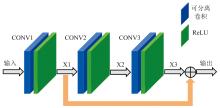
图1 深度可分离卷积高阶残差网络拓扑结构Fig.1 Topological structure of the DSC-HORN

1.2 残差子模块网络模型

DSC-HORN的拓扑结构中, 各残差模块遵循相似的结构(深度可分离卷积+残差连接), 但其具体参数(通道数、 步幅)是根据不同层次特征提取需求进行设置的。 图2展示了残差子模块的内部结构, 其输入依次经过CONV1、 CONV2和CONV3卷积后生成中间特征X1、 X2和X3。 为确保信息有效传递与融合, 模块内部采用残差连接, 灰色操作符表示对X1与X3进行求和, 生成包括低层和高层特征的最终输出。

图2 残差子模块网络模型拓扑结构Fig.2 Topological structure of the residual submodule network model

这种设计保留了输入的低层信息并与高层特征结合, 实现多层次的信息提取, 显著提升了特征表达能力。 深度可分离卷积被设计用于显著降低模型的计算复杂度和参数规模, 其架构由深度卷积和逐点卷积两部分组成。 其工作原理是将每个输入通道独立地进行卷积(深度卷积), 不跨通道进行卷积操作, 从而提取通道内部的特征; 然后在每个位置使用1× 1 的卷积核将所有通道的信息组合在一起(逐点卷积), 实现跨通道的信息整合。

标准卷积的参数量P1为

P1=M×N×Cin×Cout(1)

而深度可分离卷积的参数量P2为

P2=M×N×Cin+1×1×Cin×Cout(2)

式中, M× N是卷积核的大小, Cin是输入通道数, Cout是输出通道数。 深度卷积通过在空间维度上对每个通道独立执行卷积操作, 有效减少了空间计算负担; 逐点卷积则在通道维度上实现特征的线性组合, 进一步压缩计算开销, 同时保持关键信息的完整性。 与传统卷积操作相比, 深度可分离卷积在减少参数数量的同时, 大幅提升了计算效率, 使其在资源受限的环境下更具有优势。

1.3 DSC-HORN模型的运行环境和参数

本研究提出的DSC-HORN模型的网络参数结构如表1所示。 模型运行环境为: CPU: Intel(R) Core(TM) i7-9750H @2.60GHz; 内存: 16 GB; 操作系统: 64-bit Windows 10 Home Edition; 编程工具: MATLAB R2023b (MathWorks, Deep Learning Toolbox, Inc)。 在本模型的设计中, 卷积层C1和各个残差模块均使用了ReLU激活函数, 以充分利用其在深度学习中的优势。 卷积层C1设置为3× 256卷积核, 步幅为1, 输出256个通道, 并应用ReLU激活函数。 这个卷积层负责提取初始特征, 并在激活后将负值截断为零, 保留正特征值, 从而生成稀疏、 有效的特征表示。

表1 DSC-HORN模型每层网络结构参数 Table 1 Network structure parameters of each layer in the DSC-HORN model

在残差模块中, ReLU激活函数主要用于激活深度卷积和逐点卷积的输出。 在不同的残差模块之间, 模型引入了卷积调整层。 例如, 从残差模块1到残差模块2的通道调整层将通道数从128减少到64, 通过一个1× 64的卷积核实现。 这些卷积调整层的设计使得主分支和残差分支的输出维度匹配, 从而能够顺利进行残差连接, 并实现特征的叠加和有效融合。 通过这种分层的卷积调整和特征融合设计, 模型在优化参数量和计算效率的同时, 也保留了深度可分离卷积的优势。

2 实验部分
2.1 实验设计以及样本处理方案

为了确保在实验过程中光谱信号的稳定性, 实验在室温(约25 ℃)和相对湿度(约55%)的环境条件下进行, 以尽量减小温湿度波动对光谱数据的影响。 光谱数据采集使用便携式傅里叶红外光谱仪ALPHAPEC5010, 配备材质为ZnSe的衰减全反射附件, 设备由中船重工安谱(湖北)仪器有限公司提供。 在实验开始之前, 首先启动便携式傅里叶红外光谱仪ALPHAPEC5010, 进行约2 min的预热, 以保证设备的稳定运行。 接着, 将样品放置在检测位置启动光谱采集程序。 利用FTIR Spectrometer软件, 仪器自动进行光谱数据的采集及傅里叶变换, 并生成吸光度光谱。

实验所用试剂包括甲基膦酸二甲酯(Dimethyl methylphosphonate, DMMP; AR级)以及二氯甲烷(AR级), 均购自北京化工厂。 从实际场景中采集了11种地物样本作为背景参考, 包括细叶结缕草、 地毯草、 杨树叶子、 柳树叶子、 泥土、 沙石、 自来水、 雨水、 石英玻璃、 硬纸板和二氯甲烷。 各类地物样本的处理过程有所不同, 对于植物样本(细叶结缕草、 地毯草、 杨树和柳树叶子), 首先通过清洗去除表面尘土与杂质, 以确保其不含外部污染物, 随后将样本自然晾干, 并根据测量要求切割成适当的尺寸。 泥土和沙石样本则经过筛子粗筛以去除杂质。 自来水和雨水样本在采集后不需要额外处理, 直接进行光谱分析。 石英玻璃样本使用超声波清洗机去除表面污物, 硬纸板样本则用剪刀裁剪至适当的尺寸, 对于二氯甲烷样本则直接使用纯二氯甲烷试剂进行实验。

2.2 光谱数据处理

采集了11种地物样本的光谱数据, 得到的光谱曲线如图3(a)所示。 为了尽量减少因人为操作或实验误差等因素导致的数据偏差, 每种地物样本在相同条件下重复采集20次, 共获得220组背景地物光谱数据。 此外, 实验利用纯净水配制了六种不同浓度梯度的DMMP溶液, 并通过光谱测量确定了其在1 050 cm-1附近的显著吸收峰, 对应于磷氧碳(P— O— C)键的伸缩振动, 如图3(b)所示。 为更贴近实际爆炸或化学品泄漏场景中低浓度残留DMMP的环境特征, 同时保留其显著吸收峰并增加模型识别难度, 选取10%浓度的DMMP溶液, 分别滴加至11种地物背景样本中采集混合光谱数据。 每类样本在相同实验条件下重复采集30次, 以确保数据稳定性和代表性, 最终获取330组混合光谱数据。 图4显示了10% DMMP溶液在11种地物背景下的光谱曲线。 可以观察到, 在不同背景条件下, 10%浓度的DMMP的光谱曲线受到显著干扰。

图3 背景地物和不同浓度DMMP的光谱曲线
(a): 11类背景地物的光谱曲线; (b): 6种不同浓度DMMP的光谱曲线Fig.3 Spectral curves of background materials and DMMP at different concentrations
(a): Spectral curves of 11 background objects; (b): Spectral curves of DMMP with six different concentrations

图4 10%浓度DMMP在不同地物背景下的混合光谱曲线Fig.4 Spectra of 10% DMMP mixed with different background materials

在数据采集过程中, 难以完全避免由于仪器性能和环境波动引起的异常数据。 为此, 针对每类样本数据, 基于马氏距离法对光谱数据进行异常值检测, 计算各样本点与数据均值的距离, 设定阈值剔除偏离值, 确保数据集质量和分析结果的可靠性。 共检测剔除了22组异常样本, 其中包括10组背景地物光谱数据和12组混合光谱数据。 随后根据光谱样本是否含有危险化学品将其划分为两种标签, 标签0表示样本中基本不含危险化学品, 因此不触发警示; 而标签1表示样本中含有一定量的危险化学品, 此时触发警示, 自动发出声光警报。

最终, 构建了包含528组样本数据的光谱数据集, 并基于分层随机抽样方法, 将数据集按照6:1:3的比例划分为训练集、 验证集和测试集(见表2)。 分层随机抽样方法在数据集划分过程中, 可以确保两类标签样本在各子集中保持均衡分布, 从而能够更真实地反映数据的整体分布特征。

表2 数据集样本划分表 Table 2 The dataset sample partition table
2.3 评价指标

为评估和比较不同模型的性能, 采用准确率(Accuracy, ACC)、 精准率(Precision, PRE)、 召回率(Recall, REC)、 特异性(Specificity, SPE)以及F1分数(F1-Score, F1)等指标。 ACC是识别模型常用的整体性能指标, 用于衡量模型的总体准确度; PRE则表示正样本预测的准确性, 用于评估模型的精确率; REC表示对正样本的识别能力(即召回率), 用于评估模型的敏感性和漏报率; SPE衡量对负样本的识别能力, 反映模型的特异性及误报率; F1分数是PRE和REC的调和平均值, 可以衡量模型精确性与敏感性的综合表现, 其值越接近1, 模型性能越优。 相应指标的计算公式如式(3)— 式(7)

ACC=TP+TNTP+TN+FP+FN(3)

PRE=TPTP+FP(4)

REC=TPTP+FN(5)

SPE=TNTN+FP(6)

F1=2×PRE×RECPRE+REC(7)

式(3)— 式(7)中, TP(真阳性)表示正确预测为该类的样本数量, TN(真阴性)表示正确预测为非该类的样本数量, FP(假阳性)表示错误预测为该类的样本数量, FN(假阴性)表示错误预测为非该类的样本数量。 此外, 为更直观地分析和评估各类别的识别结果, 尤其是类别不平衡的数据, 常采用多分类混淆矩阵[14](multi-label confusion matrix, MCM)的方式。 混淆矩阵是一种特殊的交叉表格, 矩阵主对角线上的值表示预测与实际一致的样本数量, 而非主对角线上的值则表示预测与实际不符的样本数量。

3 结果与讨论
3.1 DSC-HORN模型识别效果与分析

在模型构建过程中, 数据集需系统划分为三个互斥子集以实现模型的科学评估。 训练集通过迭代优化算法驱动模型参数的学习过程, 使其逐步捕获数据的内在特征; 验证集承担超参数优化与模型结构筛选的任务, 通过监控其损失曲线动态调整学习策略, 从而抑制对训练数据的过度拟合; 最终阶段则通过测试集的综合性能指标对模型的泛化能力进行最终评估, 该过程严格遵循仅单次评估原则以确保结果的统计学意义。 这种分层评估机制通过数据隔离策略有效防止信息泄露, 为模型性能的客观量化提供了可靠保障。

图5展示了DSC-HORN模型的训练与验证过程, 训练集准确率在初期迅速提升, 于100轮后趋于收敛, 接近100%, 表明模型对训练数据具有强大的学习能力。 验证集准确率在前20轮内快速提高, 随后逐步稳定在较高水平, 显示出模型的良好拟合能力。 此外, 训练集和验证集的损失值均随着训练轮次的增加逐渐下降, 并于130轮次后趋于稳定。 训练损失曲线在初期下降较快, 说明模型能够迅速学习全局特征。 验证集的损失曲线下降平稳, 最终趋于稳定, 表明模型在未见数据上的泛化性能较强。 验证集损失与训练集损失曲线未出现显著偏差, 表明过拟合现象较少。 为进一步评估DSC-HORN模型的稳定性和鲁棒性, 采用了十折交叉验证方法。 结果表明, 该模型在所有折上的训练集平均准确率为98.98%, 验证集平均准确率为93.66%, 测试集平均准确率为95.06%, 显示出DSC-HORN在不同数据集划分情况下具有高度一致的识别能力, 这一结果进一步证明了模型的可靠性和优越的泛化能力。

图5 DSC-HORN模型训练与验证过程Fig.5 Training and validation process of the DSC-HORN model

3.2 不同模型的性能对比

利用训练好的DSC-HORN模型对158个测试样本进行实际验证。 为全面评估DSC-HORN模型的性能, 与其他多种模型进行了对比, 包括传统的K-最邻近算法(K-nearest neighbors, KNN)模型, 以及随机森林(random forest, RF)、 鲁棒众数回归稀疏非负矩阵分解(mode regression non-negative matrix factorization, MR-NMF)、 反向传播神经网络(backpropagation neural network, BP)模型, 还有深度学习领域的1D-CNN(1D-convolutional neural network)识别模型。 其他对比模型同样采用十折交叉验证, 图6显示了某次测试集交叉验证结果的混淆矩阵。 从图6可以看出, DSC-HORN在158个样本中仅误判5个, 是所有模型中误判样本数最少的。

图6 不同模型的分类混淆矩阵Fig.6 The multi-label confusion matrices of different models

表3展示的各模型的性能指标及预测耗时, 表明了DSC-HORN模型在多个指标上优于传统模型。 DSC-HORN的ACC达到96.84%, 比1D-CNN提高6.33%, 比BP提高10.76%, 比MR-NMF提高5.07%, 比RF提高13.93%, 比KNN提高5.7%, 表现出显著的准确率优势。 此外, DSC-HORN在其他指标上也表现优异, 如PRE达到95.05%, REC达到100%, SPE达到91.94%, 以及F1为97.46%。

表3 不同模型的性能指标 Table 3 Performance metrics of different models

综合分析表明, DSC-HORN在多个性能指标上表现最佳, 能够高效识别正类与负类, 展现了卓越的识别能力。 相比之下, MR-NMF和KNN在综合性能上表现较好, 但分别存在负类误报和正类漏检的问题, 如表3所示, MR-NMF的误报率较高, 而KNN的正类召回率低于其他模型; 尽管1D-CNN 模型在正类召回率上达到了100%, 但其负类特异性较低, 仅为75.81%(表3所示), 明显低于DSC-HORN模型的91.94%, 较高的误报率限制了1D-CNN模型在实际应用中的实用性; 而RF和BP的整体表现中规中矩, 各项指标均低于DSC-HORN。 因此, DSC-HORN凭借其均衡且卓越的性能成为最优选择。

3.3 深度可分离卷积的优势

本研究在DSC-HORN算法中引入了深度可分离卷积[13]这一策略(depthwise separable convolution), 显著优化了计算效率。 选取基于模型实际应用场景中典型光谱数据的通道数量和卷积核大小, 当输入通道数为400、 输出通道数为128、 卷积核大小为3时, 根据式(1)和式(2)进行计算, 结果显示: 标准卷积的参数量为153 600, 而深度可分离卷积仅需52 400, 减少约65.89%, 参数量的显著减少降低了内存消耗, 使DSC-HORN在资源受限环境中具有更好的适应性。 表3的预测耗时显示, 引入深度可分离卷积后, DSC-HORN的预测耗时为0.2174秒, 仅次于BP模型(0.177 4 s), 在所有模型中排名第二。 速度提升的计算基于预测耗时数据。 相比传统1D-CNN模型的预测耗时0.801 8 s, DSC-HORN模型的预测耗时减少至0.217 4 s, 缩短了0.584 4 s, 时间减少比例为72.89%, 预测速度提高约4倍。 通过引入深度可分离卷积, DSC-HORN在保留强大特征提取能力的同时, 显著减少了参数量并提升了计算效率。 相比传统卷积神经网络, DSC-HORN能够有效降低内存资源消耗和计算复杂度, 为资源受限的环境和实时应用场景提供了一种轻量化且高性能的解决方案。

4 结论

提出了一种结合深度可分离卷积与高阶残差网络的新型模型(DSC-HORN), 针对中红外光谱数据中的复杂化学品识别问题, 提出了一种较为新颖的解决方案。 该方案在理论与实验层面上均展现了创新性与应用价值。 通过结合深度可分离卷积与高阶残差网络, DSC-HORN模型有效优化了特征提取效率和识别精度。 通过实验验证, DSC-HORN模型在植被、 土壤等复杂背景中能够有效应对干扰信号, 保持高识别精度, 展现出较强的鲁棒性与环境适应能力。

综合来看, 本文提出的DSC-HORN模型不仅在光谱数据的特征提取能力和识别效率上具有优势, 还为复杂环境条件下的危险化学品监测与精准识别提供了一种高效、 可靠的解决方案。 未来工作将进一步扩展该模型在更多化学品种类及更复杂场景下的适用性, 例如针对高噪声环境设计更强鲁棒性的模块, 同时优化模型结构以适应拉曼光谱等其他类型光谱数据的分析需求。 本研究为中红外光谱技术在复杂场景中的应用开辟了新的思路, 为高维光谱数据的智能化分析提供了重要的理论支持和技术保障, 也为危险化学品的实时监测与应急响应提供了关键工具。

参考文献
[1] Zhu L, Lu S H, Zhang Y H, et al. Vibrational Spectroscopy, 2020, 109: 103071. [本文引用:1]
[2] Zhang L J, Huang X D, Fan X M, et al. Environmental Technology, 2021, 42(2): 270. [本文引用:1]
[3] Ceniti C, Spina A A, Piras C, et al. Foods, 2023, 12: 2917. [本文引用:1]
[4] De Bruyne S, Speeckaert M M, Delanghe J R. Critical Reviews in Clinical Laboratory Sciences, 2018, 55(1): 1. [本文引用:1]
[5] Wang J, Niu X, Zheng L, et al. Sensors, 2016, 16: 1941. [本文引用:1]
[6] GUO Teng-xiao, DING Xue-quan, DONG Xiao-qiang, et al(郭腾霄, 丁学全, 董晓强, 等). Computers and Applied Chemistry(计算机与应用化学), 2013, 30(1): 18. [本文引用:1]
[7] LENG Si-yu, QIAO Jia-hui, WANG Lian-qing, et al(冷思雨, 乔嘉慧, 王连庆, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(1): 303. [本文引用:1]
[8] Lee L C, Liong C Y, Jemain A A. Chemometrics and Intelligent Laboratory Systems, 2018, 182: 90. [本文引用:1]
[9] Jin X, Che J, Chen Y. IEEE Access, 2021, 9: 10940. [本文引用:1]
[10] Nassif A B, Shahin I, Attili I, et al. IEEE Access, 2019, 7: 19143. [本文引用:1]
[11] Min S, Lee B, Yoon S. Briefings in Bioinformatics, 2017, 18(5): 851. [本文引用:1]
[12] Kuutti S, Bowden R, Jin Y, et al. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(2): 712. [本文引用:1]
[13] Srivastava H, Sarawadekar K. Proceedings of 2020 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 2020, 1. [本文引用:2]
[14] Ruuska S, Hämäläinen W, Kajava S, et al. Behavioural Processes, 2018, 148: 56. [本文引用:1]