1.1.1 近红外光谱采集仪器

德国Bruker公司的Matrix-F型傅里叶变换近红外光谱仪。

1.1.2 基酒样品采集

实验样品源自中国四川某著名酒企浓香型白酒生产车间的62个不同发酵池, 上半年选择3、 4、 5月采集, 下半年选择9、 10、 11月采集。 实验采集的基酒样本根据酒质划分标准划分为一级酒、 二级酒、 三级酒以及四级酒。 基酒的等级划分先由现场工作人员初步确定, 随后交由该酒企的5名感官评定师进行再一次的综合评定。 总共采集687个酒样, 其中各等级基酒样本数依次为139、 282、 166、 100个。

1.1.3 基酒近红外光谱数据采集

采集光谱时环境温度为(20± 2) ℃, 空气相对湿度小于80%RH。 光谱采集的检测模式为透射模式, 扫描范围为12 500~4 000 cm^-1, 分辨率为8 cm^-1, 扫描次数32次, 共2 204个扫描值, 平均间隔为3.855 cm^-1, 取两次扫描结果的均值作为初始光谱。

受仪器本身原因, 初始光谱图的两端受噪声影响较大且有效信息较少, 因此截取4 300~9 000 cm^-1范围内的1 215个光谱点作为原始光谱。 为削弱仪器和环境中所带来的影响, 提高光谱数据的表征能力和信噪比, 通过9点2次卷积平滑处理基酒的原始光谱数据。 因此后续的研究均基于卷积平滑处理后的光谱数据。

原数据集分别基于X-Y距离的样本集划分(sample set partitioning based on joint X-Y distances, SPXY)、 随机划分和分层抽样划分以4∶ 1的比例划分为训练集和测试集, 并根据训练集的支持向量机(support vector machine, SVM)模型5折交叉验证准确率来选择划分方法。 其中SVM采用了一对多的分类策略, 并使用高斯核函数将数据映射至高维空间。 SVM的正则化参数C和核函数参数g采用网格搜索算法去寻找最优C和g的组合方式, 二者的搜索范围均为2^-10~2¹⁰, 并以指数步长2递增。

SHAP源于经济学家Lloyd Shapley于1953年提出的合作博弈解决方案, 每个特征对预测模型输出值的贡献度可通过对应的Shapley值来体现。 SHAP通过x=h_x(z)将x映射至z来创建简化输入z, 基于z原始模型f(x)可用二元变量的线性函数来近似

f(x)=g(z)=φ0+∑i=1Mφizi(1)

式(1)中, z={0, 1}M, M为输入特征的数量, φ ₀=f(hx(0)), φ _i是特征属性值

$\begin{array}{c} \varphi_{i}(f, x)=\sum_{S \in F \backslash\{i\}} \frac{|S|!(M-|S|-1)}{M!} \cdot \\ {\left[f_{x}(S \bigcup\{i\})-f_{x}(S)\right]} \end{array} $ (2)

$f_{x}(S)=f\left(h_{x}^{-1}(z)\right)=E\left[f(x) \mid x_{s}\right] $ (3)

式(2)和式(3)中, F是z中的非零输入集, S为F的子集, 排除了F中第i个特征, φ _i是加性特征归因的统一度量, 即Shapley值。 Shapley值满足局部准确性、 缺失性、 一致性三大性质^[17], 同时在模型参数固定时, 各特征的Shapley值是唯一的, 特征的贡献值仅由模型结构和输入样本决定。 Shapley值可表示特征与因变量间的正、 负关系和相关程度, 并且收益分配具备客观性, 因此可以作为一种有效的特征选择方法^[18]。

由于精确计算E[f(x)|x_s]的计算量与输入特征数量呈指数级增加关系, 并且近红外光谱数据中数据维度较高, 因此直接计算近红外光谱每个光谱点的Shapley值十分困难。 基于此, 本研究采用了由Lundberg等^[19]提出的一种近似方法Tree SHAP, 该方法通过决策树结构来有效计算E[f(x)|x_s]的值, 将原始计算复杂度由O(TL2^M)转换为O(TLD²), 其中T为树的数量, L为任意树的最大子叶树, D为任意树的最大树深^[20]。

本研究中将训练集中的1 215个原始光谱点作为模型输入, 并基于XGBoost算法建立预测模型(训练集准确率96.36%)。 然后将XGBoost预测模型以及自变量X作为Tree SHAP的输入, 分别获得各样本关于四种等级基酒的Shapley值矩阵V₁、 V₂、 V₃、 V₄。 随后按照图1中的流程, 设置的目标光谱点数n依次为10, 20, 30, 40, 50(n=n₁+n₂+n₃+n₄), 通过计算得到的SHAP贡献值排序来确定关于各等级基酒的特征子集Rn_i, 最后将四个子集的并集结果(剔除重复的特征光谱点)作为特征选择结果。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于Shapley值矩阵的特征选择流程 P: 样本数; q: 光谱点数; Rni: 第i个等级基酒特征光谱点集合Fig.1 Feature selection process based on the shapley value matrix P: Number of samples; q: Number of spectral points; Rni: Feature spectral point set for the i-th grade of base Baijiu

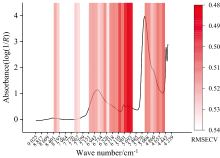
iPLS算法于2000年由Nø rgaard等^[21]提出, 其原理是将原始光谱分割为若干个子区间, 然后分别在每个子区间上进行偏最小二乘回归建模。 随后采用交叉验证计算每个区间回归模型的交叉验证均方根误差(root mean square of cross-validation, RMSECV), 并根据RMSECV值的大小选择特征区间, 子区间的RMSECV值越小则说明该区间的重要性越大。 在本研究中, 首先将训练集的1 215个光谱点依次等分为45个特征区间, 每个区间包含27个光谱点, 随后在每个区间上进行偏最小二乘回归建模, 采用留一交叉验证计算每个区间的RMSECV值。 最后基于前向特征选择确定最优特征区间数, 并选择了26特征区间作为iPLS特征选择结果。 随后按照1.4节中的SHAP特征选择方法完成特征选择(初始XGBoost模型训练集准确率100%)。

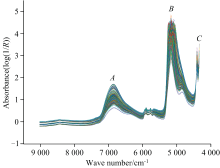
基酒中主要的成分为水分子和乙醇, 从图2中可以看出, 基酒的近红外原始光谱图形成了明显的三个吸收峰A、 B、 C。 其中A峰位于6 842 cm^-1附近, 属于水分子的一级倍频吸收峰; B峰位于5 160 cm^-1附近, 属于水分子的合频吸收峰; C峰位于4 347 cm^-1附近, 属于乙醇分子的特征吸收峰^[22]。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基酒近红外原始光谱Fig.2 Original near-infrared spectrum of base Baijiu

原基酒数据集分别采用SPXY、 随机划分和分层抽样划分并基于SVM进行5折交叉验证, 各划分方法的准确率分别为86.72%、 83.52%和83.70%, 说明SPXY为本数据集的更优划分方法。 SPXY是依据样本的光谱信息(X)和基酒等级(Y)之间的空间分布最大化来划分数据集, 因此划分结果在X-Y空间中更具有代表性, 进而模型泛化能力和预测性能更优。 SPXY划分结果见表1。

表1

Table 1

表1(Table 1)

表1 基于SPXY的数据集划分结果 Table 1 Dataset partitioning results based on SPXY 基酒等级 一类基酒 二类基酒 三类基酒 四类基酒 样本总数 139 282 166 100 训练集样本数 115 224 128 82 测试集样本数 24 58 38 18

表1 基于SPXY的数据集划分结果 Table 1 Dataset partitioning results based on SPXY

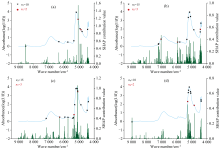
原始光谱经SHAP特征选择后, 依次得到10、 18、 26、 36、 40个特征光谱点, 图3和图4展示了n等于10和50时的各等级基酒选择结果以及最终特征光谱点的分布。 随后对特征选择结果依次采用XGBoost和LightGBM算法建模的测试集结果如图4。 结果表明LightGBM预测准确率整体上优于XGBoost, 在36和40个特征光谱点时准确率较高。 为验证模型的稳定性和泛化能力, 对各特征选择结果分别基于XGBoost和LightGBM算法进行5折交叉验证计算准确率均值, 结果见表2。 各数据集的5折交叉验证结果表明LightGBM模型的表现整体上仍优于XGBoost。 并且5折交叉验证与SPXY的结果表现出较为一致的趋势, 预测性能整体随特征数的增加而增加, 当特征数为40时, XGBoost和LightGBM模型的交叉验证准确率均为最高。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 各等级基酒的SHAP贡献值及特征分布 (a): 一类基酒; (b): 二类基酒; (c): 三类基酒; (d): 四类基酒Fig.3 SHAP contribution values and feature distribution for each grade of base Baijiu (a): Grade 1 base Baijiu; (b): Grade 2 base Baijiu; (c): Grade 3 base Baijiu; (d): Grade 4 base Baijiu

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 SHAP特征选择结果 (a): 特征分布; (b): 模型测试集结果Fig.4 Results of SHAP feature selection (a): Feature distribution; (b): Model test set results

表2

Table 2

表2(Table 2)

表2 基于SHAP特征选择的交叉验证结果 Table 2 Cross-validation results of feature selection based on SHAP 特征光谱数 10 18 26 36 40 XGBoost验证结果/% 91.50 92.25 93.67 94.39 94.54 LightGBM验证结果/% 94.12 95.13 94.40 95.01 96.25

表2 基于SHAP特征选择的交叉验证结果 Table 2 Cross-validation results of feature selection based on SHAP

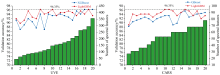
为进一步探讨SHAP在特征选择中的可行性与优势, 本研究引入两种主流的光谱特征选择算法UVE和CARS进行对比分析。 参数设置时, 首先训练集数据经蒙特卡洛模拟500次结合5折交叉验证确定偏最小二乘模型的最优潜变量数为9。 在此基础上, UVE噪声服从均值0.4、 标准差0.25 的正态分布, CARS的迭代次数为50, 对二者20次重复计算后结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 UVE和CARS特征选择结果Fig.5 UVE and CARS feature selection results

从特征选择结果来看, UVE选择的特征数在199.5± 155.5之间波动, CARS选择的特征数在52.5± 25.5之间波动。 可看出无论是UVE还是CARS, 其特征选择结果在特征数量上均表现出了一定的不确定性, 具体表现为在相同数据集和参数下, 重复运行后得到的特征光谱点波数及数量具有较大的波动性, 且特征光谱数难以控制。 而SHAP的唯一性保证了在固定模型参数以及输入时特征选择结果保持一致。 并且SHAP在特征选择时依据的是光谱点的贡献值排序, 因此模型的透明度较高, 可通过特征集所构建模型的预测性能灵活调整特征数。 因此, 从特征选择的确定性、 透明度和灵活性来看, 基于SHAP的特征选择方法具备一定的优势。 从模型性能方面, UVE和CARS的最高测试集准确率均为96.35%, 其中UVE最低在101个特征光谱点时达到了最高预测性能, 而CARS最低在53个特征光谱点时达到了最高预测性能。 相比之下, SHAP以36个特征光谱点实现了97.08%的测试集准确率, 在更少特征数的前提下表现出了更高的模型预测性能。

值得注意的是, 采用SHAP特征选择时, 其核心是计算各特征对于模型输出的边际贡献来衡量特征的重要性。 并且SHAP是通过已训练模型的输出评估特征(事后解释方法), 模型的预测性能将直接影响特征选择的效果。 因此当训练模型的预测性能较低时可能会错误学习数据中特征与标签之间的关系, 进而导致光谱点的SHAP贡献值排序可能无法准确反映特征与标签的真实关系。 所以在SHAP特征选择时, 提高已训练模型预测性能对于正确学习数据中特征与标签之间的关系有积极意义。 基于这一考虑, 本研究提出了先采用iPLS对原始光谱数据进行初步特征选择, 再采用SHAP特征选择的混合策略。 以提高SHAP值计算时训练模型的预测性能, 并进一步探讨本数据中是否存在Fryer等^[23]所指出的SHAP贡献值排名与预测性能排名可能不一致的情况。

原始光谱经SHAP特征选择后, 依次得到9、 18、 26、 33、 38个特征光谱点, 图7为SPXY测试集结果, 表3为各数据集的5折交叉验证结果。 综合图7和表3中的内容可以看出iPLS-SHAP特征选择结果的模型性能整体上优于单独使用SHAP的特征选择结果。 并且采用LightGBM建模时, iPLS-SHAP选择的9个特征达到了99.27%的测试集准确率和98.75%的交叉验证准确率, 为最优预测模型。 为论证结果的显著性和避免偶然性, 对iPLS-SHAP结果的9特征集与SHAP选择结果的36、 40特征集分别采用5折交叉验证并重复10次, 对各自50组配对结果采用配对t检验进行显著性分析。 结果表明9特征集与36、 40特征集之间的差异均具有统计显著性(p< 0.05), 说明iPLS-SHAP特征选择的最优特征集的模型性能高于单独使用SHAP的最优特征集。

图6和图7中可看出, iPLS滤去了4 443~4 343和5 588~5 172 cm^-1等光谱区域, 尽管这些区域中分布着SHAP贡献值较高光谱点, 并将原本存在这些区域的特征光谱点由RMSECV更低区域内SHAP贡献值相对更低的光谱点替换。 如n=10时, 采用SHAP特征选择的特征光谱点中4 432、 5 276和5 330 cm^-1被iPLS-SHAP选择的5 014和5 049 cm^-1所替换后, XGBoost和LightGBM模型的测试集准确率分别上升了0.73%和4.91%。 说明经iPLS初筛后再采用SHAP特征选择的模型性能更优, 也就是说部分SHAP贡献值较高的光谱点由SHAP贡献值相对较低的光谱点替换后可以提高模型的预测性能。 所以iPLS-SHAP混合策略表现更优的原因可能是: 采用iPLS可以初步滤去对模型预测性能的提升有限但包含多个高SHAP贡献值光谱点的光谱区间以及冗余区间, 并提高SHAP值计算时的训练模型性能。 从而有利于SHAP值计算时正确学习光谱点与标签的关系, 以及选取部分SHAP贡献值相对更低但对模型预测性能提升相对更高的光谱点。 上述结果表明: SHAP贡献值并不完全是模型预测性能的直接指标, 即特征光谱点的SHAP贡献值排名与模型预测性能排名并不严格一致, 但基于SHAP贡献值进行特征选择是可行的, 这与Van等^[24]的研究结果相似。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 iPLS特征选择结果Fig.6 iPLS feature selection results

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 iPLS-SHAP特征选择结果 (a): 特征分布; (b): 模型测试集结果Fig.7 iPLS-SHAP feature selection results (a): Feature distribution; (b): Model test set results

表3

Table 3

表3(Table 3)

表3 基于iPLS-SHAP特征选择的交叉验证结果 Table 3 Cross-validation results of feature selection based on iPLS-SHAP 特征光谱数 9 18 26 33 38 XGBoost验证结果/% 94.68 95.56 96.44 95.27 95.00 LightGBM验证结果/% 98.75 97.31 96.16 97.14 96.43

表3 基于iPLS-SHAP特征选择的交叉验证结果 Table 3 Cross-validation results of feature selection based on iPLS-SHAP

上述iPLS筛选剔除的高SHAP值光谱点中, 4 432 cm^-1可能与基酒中醇类的C— H伸缩振动的第二泛频相关; 5 276和5 330 cm^-1可能与基酒中水和醇的O— H吸收相关, 表明剔除的3个光谱点主要与基酒中水和醇类物质含量相关^[25]。 以水分和乙醇为代表的各类醇不仅是基酒中的主要成分, 也是摘酒工艺中不同等级基酒间显著特征之一, 因此与其相关的光谱点SHAP贡献值可能较高。 在基酒近红外光谱中, 水和醇类物质的特征吸收峰较宽(如O— H伸缩振动和O— H弯曲振动的组合频覆盖4 550~5 550 cm^-1)且SHAP选取的多个特征点在此范围内。 该结果可能会导致基于SHAP值排序的特征选择结果存在信息冗余, 即过多特征点用于表达基酒中水和醇的物质信息, 而丢失了基酒中其他微量物质信息。 在白酒的摘酒工艺中, 基酒等级的划分不仅需要考虑水和醇类等显著物质的变化, 还需要考虑酸、 酯等微量物质对基酒口感和香气的影响。 iPLS-SHAP筛选的5 014 和5 049 cm^-1光谱点虽然SHAP值相对较低, 但其不仅可能与水和醇的O— H伸缩振动和O— H弯曲振动的组合频相关, 还可能与基酒中羧酸的C— H弯曲振动和O— H伸缩振动组合频相关。 Harris等^[26]也指出, 这两个光谱点所在区域的吸光度可能与酒中羧酸含量相关。 因此5 014和5 049 cm^-1 可能不仅表达基酒中醇的物质信息, 还可能表达基酒中羧酸的物质信息。 因此部分光谱点高SHAP贡献值但低预测贡献的潜在机理为: 仅通过高SHAP值进行特征选择可能会导致光谱特征冗余, 进而掩盖了基酒各组分间的协同和交互作用, 从而模型性能欠佳。

iPLS-SHAP混合选择策略可以将两种特征选择算法的优势相结合, iPLS针对模型的预测性能对光谱区间进行初步的选择, 以剔除冗余区间。 SHAP则根据光谱点对模型输出的贡献值排名去选择特征光谱点, 大幅降低了光谱数据的维度且有效保留与基酒等级划分的关键信息。 并且在采用iPLS算法进行特征区间选择时, 本研究采用的是留一交叉验证的方法去计算每个光谱区间的RMSECV值, 即每个样本依次作为了测试集, 从而保证重复运行时每个区间RMSECV值的确定, 进而保证区间选择结果的确定。 结合SHAP值的唯一性, 所以本研究所提出的iPLS-SHAP特征选择策略也是一种具备确定性特征选择方法。