GBAII-DASH中消除莫尔条纹对高层大气测风精度的影响

引用本文

惠宁菊, 王彦龙, 李文文, 刘洋河, 李存霞, 章艺珊, 符迪迪, 唐远河. GBAII-DASH中消除莫尔条纹对高层大气测风精度的影响[J]. 光谱学与光谱分析, 2025,45(8): 2266-2272.
HUI Ning-ju, WANG Yan-long, LI Wen-wen, LIU Yang-he, LI Cun-xia, ZHANG Yi-shan, FU Di-di, TANG Yuan-he. Eliminating the Influence of Moiré Fringes on Upper Atmospheric Wind Measurement Accuracy in GBAII-DASH[J]. Spectroscopy and Spectral Analysis, 2025,45(8): 2266-2272.
Doi:10.3964/j.issn.1000-0593(2025)08-2266-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

GBAII-DASH中消除莫尔条纹对高层大气测风精度的影响

惠宁菊^1,², 王彦龙¹, 李文文¹, 刘洋河³, 李存霞^1,², 章艺珊¹, 符迪迪¹, 唐远河^1,^*

1.西安理工大学理学院, 陕西西安 710048

2.陕西省超快光电与太赫兹科学重点实验室, 陕西西安 710048

3.西安理工大学机械与精密仪器工程学院, 陕西西安 710048

*通讯作者 e-mail: ltp1801@163.com

作者简介: 惠宁菊, 女, 1986年生, 西安理工大学理学院讲师 e-mail: huiningju@163.com

收稿日期: 2024-09-24 修回日期: 2025-03-20

基金: 国家自然科学基金项目(41975040), 陕西省教育厅青年创新团队项目(24JP114), 陕西省自然科学基础研究计划项目(2025JC-YBMS-059), 山东大学晶体材料国家重点实验室2024年开放课题项目(KF2411)资助

摘要

为了提高中高层大气风速的探测精度, 研制了Ground Based Airglow Imaging Interferometer-Doppler Asymmetric Spatial Heterodyne Spectroscopy(GBAII-DASH)成像干涉系统, 研究了其产生的周期性干涉直条纹与阵列CCD探测器以一定耦合角重叠时所产生的莫尔条纹对系统测风精度的影响, 提升了系统的测风精度。分析了GBAII-DASH系统莫尔条纹的成因。利用“四强度法”和“傅里叶变换法”两种方法, 从不同耦合角度下产生的包含莫尔条纹的干涉图中提取了正演风速, 得到平均测风相对误差分别为3.07%和6.89%, “四强度法”具有更高的测风精度。利用频谱分析方法模拟了莫尔条纹对CCD探测器的像素和GBAII-DASH系统的干涉条纹两者空间频率的差值大小的依赖关系, 发现增大两者差值可改善莫尔条纹对测风精度的影响。在实验室内得到了有、无莫尔条纹的两种干涉图, 并将室外探测的测风结果与西安上空90~100 km的过境卫星仪器Thermosphere-Ionosphere-Mesosphere Energetics and Dynamics Doppler Interferometer(TIDI)的观测结果进行了比较, 发现GBAII-DASH与TIDI探测西安上空90~100 km的大气风速误差仅为0.3 m·s^-1。由此可见, 消除莫尔条纹后再利用“四强度法”确实大大提高了系统的测风精度。

关键词: 莫尔条纹; 测风精度; “四强度法”测风

中图分类号:P164 文献标志码:A

Eliminating the Influence of Moiré Fringes on Upper Atmospheric Wind Measurement Accuracy in GBAII-DASH

HUI Ning-ju^1,², WANG Yan-long¹, LI Wen-wen¹, LIU Yang-he³, LI Cun-xia^1,², ZHANG Yi-shan¹, FU Di-di¹, TANG Yuan-he^1,^*

1. School of Science, Xi'an University of Technology, Xi'an 710048, China

2. Key Laboratory of Ultrafast Photoelectric Technology and Terahertz Science in Shaanxi, Xi'an 710048, China

3. School of Mechanical and Precision Instrument Engineering, Xi'an University of Technology, Xi'an 710048, China

*Corresponding author

Abstract

To enhance the detection accuracy of wind speed in the middle and upper atmosphere, GBAII-DASH (Ground-Based Airglow Imaging Interferometer-Doppler Asymmetric Spatial Heterodyne Spectroscopy) imaging interferometer system was developed. The influence of Moiré fringes generated when the periodic interference of straight fringes produced by the system overlapswith the array CCD detector at a certain coupling angle on the wind measurement accuracy of the system was studied, and the wind measurement accuracy of the system was improved. This paper analyzed the cause of Moiré fringes in the GBAII-DASH system. Using the “Four-point algorithm” and the “Fourier transform method”, the forward wind speed was extracted from the interference patterns containing Moiré fringes generated at different coupling angles. The average relative wind measurement errors were 3.07% and 6.89% respectively, so the “Four-point algorithm” had higher wind measurement accuracy. The spectral analysis method simulated the relationship between the difference in spatial frequency between the Moiré fringes and the interference fringes of the GBAII-DASH system and the CCD detector. It was found that increasing the difference could improve the influence of the Moiré fringes on the wind measurement accuracy.The laboratory obtained two types of interference patterns with and without moiré fringes. The wind speed measurement results detected outdoors were compared with the observations of the satellite instrument TIDI (Thermosphere-Ionosphere-Mesosphere Energetics and Dynamics Doppler Interferometer) passing over Xi'an at an altitude of 90~100 km. It was found that the wind speed error of the GBAII-DASH and TIDI in detecting the atmosphere above Xi'an at 90~100 km was only 0.3 m·s^-1. Thus it can be seen that eliminating the moiré fringes and then using the “Four-point algorithm” greatly improves the system's wind measurement accuracy.

Keyword: Moiré fringes; Wind measurement accuracy; “Four-point algorithm”

文章图片

0. 引言

为了提高地球中高层(60~300 km)及行星大气风速的探测精度, 科技工作者一直在努力探寻新系统和新方法。 1991年, 美国发射的Upper Atmospheric Research Satellite(UARS)卫星上搭载的High Resolution Doppler Imager(HRDI)采用3个高、中、低分辨率的法布里-波罗干涉仪(Fabry-Polo Interferometer, FPI)探测地球上空10~110 km的大气, 以波长630.0、 690.0和762.0 nm的气辉为目标光源的测风精度可达5 m· s^-1[1]。 UARS上搭载的广角迈克尔逊干涉仪(Michelson Interferometer, MI)的Wind Imaging Interferometer(WINDII)利用压电陶瓷驱动MI一臂的反射镜产生四分之一波长的步进技术实现“ 四强度法” 测风, 以波长557.0、 630.0、 762.0和732.0 nm的气辉为目标光源, 探测地球上空80~300 km的大气风速精度为10 m· s^-1[2], WINDII和HRDI相互重叠30 km大气区域相互验证的探测结果证明FPI和MI两种仪器均具优良品质^[3]。于2001年发射且还在轨服役的TIDI仪器, 结合WINDII和HRDI的优点, 探测地球上空60~300 km中的557.7、 630.0和732.0 nm等多条气辉谱线的测风精度可达3 m· s^-1[4]。为了提高仪器分辨率^[5]、稳定性和测风精度, 2019年搭载在Ionospheric connection explorer(ICON)卫星上的Michelson Interferometer for Global High-resolution Thermospheric Imaging(MIGHTI)^[6]探测90~300 km的大气风速, MIGHTI采用Doppler Asymmetric Spatial Heterodyne Spectroscopy(DASH)^[7]思路, 将广角MI两臂的反射镜替换为闪耀光栅实现静态测风, DASH采用傅里叶变换法探测高层大气风速^[7], MIGHTI的测风精度达1.2~4.7 m· s^-1[6]。 2022年中科院光电所提出用DASH干涉仪测速时的复合光程差相移求解算法, 可将测风误差控制在5.0%以内^[8]。

2012年, 我们课题组研制了地基气辉成像干涉仪(Ground Based Airglow Imaging Interferometer, GBAII), 将广角MI和窄带FPI揉合在一起的GBAII成功探测了西安上空90~100 km的大气风速、温度、体发射率、重力波等物理量^{[9, 10, 11, 12]}, 探测目标光源是峰值高度为94 km的O₂(0-1) 865.2~867.9 nm和峰值高度在98 km的O(¹S)557.7 nm气辉, 2016年改进系统后, 测风精度可达4~6 m· s^-1[1]。为了实现静态探测且把GBAII探测气辉的干涉圆环变为直条纹, 我们将GBAII的MI两臂的反射镜换为闪耀光栅, 从而实现两臂衍射光的波阵面之间形成夹角, 构成了GBAII-DASH光学系统, 我们提出DASH系统可用“ 四强度法” 测风, 它与目前国际上流行的DASH傅里叶变换法测风相比具有更高精度^[13]。鉴于GBAII-DASH使用的面阵CCD和MI两臂的闪耀光栅这3个元件均为离散型周期性结构的器件, 其成像干涉图中将可能出现莫尔条纹, 故有必要研究消除GBAII-DASH系统中莫尔条纹的方法, 以提高GBAII-DASH系统的测风精度。

1 消除GBAII-DASH成像系统中莫尔条纹

1.1 GBAII-DASH干涉成像系统的莫尔条纹

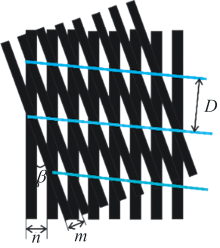
18世纪由法国莫尔(Jacques Moiré )发现并命名的莫尔条纹, 是将两个具有周期性的图像或者结构按照一定的夹角重叠放置时可能出现的明暗交替排列的条纹。我们在室内搭建如图1所示的GBAII-DASH系统, 用532 nm的激光器作为光源, 先通过光纤传输, 然后利用视场光阑及透镜得到平行光, 经1∶ 1的分束棱镜(BS)反射和透射后得到两束平行光, 再分别经过两臂上的闪耀光栅(Grating₁和Grating₂)衍射后返回分束棱镜, 经BS透射和反射后, 这两束相干光叠加将得到干涉直条纹, 成像在CCD探测器上。理论上GBAII-DASH干涉仪应拍摄到明暗相间、周期性排列的干涉直条纹, 但由于面阵型CCD探测器也是具有周期性结构的光敏元件, 所以CCD探测器在获取干涉图的过程中, 实际上是一个离散阵列对另一个不同空间频率的离散阵列的采集过程, 两组离散阵列重叠在一起时可能产生莫尔条纹, 导致CCD拍摄的成像干涉图的强度分布不均匀。下面采用几何遮光阴影原理研究GBAII-DASH系统中的莫尔条纹规律。

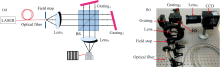	Figure Option View Download New Window
	图1 GBAII-DASH的光路图 (a): 光路图; (b): 实物图Fig.1 Optical path of GBAII-DASH (a): Optical path; (b): Picture of GBAII-DASH

假设栅距分别为m和n的两光栅, 它们形成莫尔条纹的几何模型如图2所示, 莫尔条纹宽度为

$D = \frac{mn}{\sqrt[]{m^{2} + n^{2} - 2 mn \cos β}}$ (1)

式(1)中, β 是两光栅之间的夹角。考虑到光栅的栅距m和n已知, 故式(1)中莫尔条纹宽度随β 的改变而改变。将形成图2莫尔条纹的两个光栅均看作余弦光栅, 因为光栅透过率函数为

$T_{0} = \frac{1}{2} \cos (1 + \vec{k} \vec{x})$ (2)

式(2)中, $\vec{k}$ 为光栅的波矢量, $\vec{x}$ 为横坐标。

	Figure Option View Download New Window
	图2 莫尔条纹的几何模型Fig.2 Geometric model of Moiré fringes

图1所示的GBAII-DASH系统中有两个光栅Grating₁、 Grating₂及可看作光栅的面阵CCD, 我们把经Grating₁、 Grating₂衍射后叠加所产生的明暗相间的干涉直条纹看作一个复合光栅, 其栅距为m, 并设透过率为T₁, 把CCD看作一个光栅, 其栅距为n, 设透过率为T₂, 故GBAII-DASH系统总透过率为

$T = T_{1} \times T_{2}$ (3)

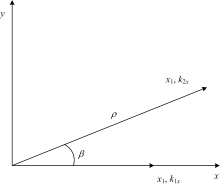
建立如图3所示的光栅叠加向量坐标轴, 其中下标1代表栅距为m的复合光栅, 即GBAII-DASH所形成的干涉直条纹, 下标2代表栅距为n的CCD探测器, β 是两光栅之间的耦合角度, ρ 代表两个光栅的周期比, 则式(3)变为

$T = \frac{1}{4} (1 + \cos {\vec{k}}_{1 x} {\vec{x}}_{1}) (1 + \cos {\vec{k}}_{2 x} {\vec{x}}_{2})$ (4)

	Figure Option View Download New Window
	图3 光栅叠加的向量坐标轴Fig.3 Vector axes of the grating overlay

因为 ${\vec{k}}_{1 x} {\vec{x}}_{1} = kx, {\vec{k}}_{2 x} {\vec{x}}_{2} = ρk (x \cos β + y \sin β),$ 展开式(4)可得标量透过率函数为

$T = \frac{1}{4} {1 + \cos kx + \cos [ρk (x \cos β + y \sin β)]} + \frac{1}{8} {\cos [kx (1 + ρ \cos β) + kyρ \sin β] + \cos [kx (1 - ρ \cos β) - kyρ \sin β]}$ (5)

我们根据参数文献[14]的思路, 进行坐标旋转后, 得到透过率式(5)中的5个波数: ∞ 、 1、 ρ 、 $\sqrt[]{1 + 2 ρ \cos β + ρ^{2}}$ 、 $\sqrt[]{1 - 2 ρ \cos β + ρ^{2}}$ ; 这5个波数的第一项是式(5)常数1对应波数, 第二和第三项分别是两个光栅的波数, 第四和第五项是因为两个光栅相互作用所产生的波数, 其中第五项的波数最小, 是分析莫尔条纹所需的量。

1.2 莫尔条纹影响GBAII-DASH测风精度的正演研究

仪器的正演研究是根据干涉系统参数及其原理用计算机模拟得到干涉结果。为了研究莫尔条纹对GBAII-DASH干涉系统的测风精度的影响, 我们用MATLAB模拟了大气风速为50 m· s^-1的GBAII-DASH光学系统的干涉直条纹, 以557.7 nm的气辉波长为例(如图4所示)。其中取干涉直条纹周期为3个像素(单像素24 μ m), 而把CCD探测器看作是栅距为2个像素间距的光栅, 故式(5)中的光栅周期比ρ =1.5。图4模拟的耦合角度分别为 0° 、 1° 、 4° 和19° , 从结果可见两种典型情况: 图4(a)和(b)是两光栅的耦合角分别为0° 和1° , 此时形成纵向莫尔条纹; 图4(c)和(d)是两光栅的耦合角分别为4° 和19° , 此时形成横向莫尔条纹, 其他耦合角度情况均与图4所列结果相似。

Figure Option
View Download New Window

图4 GBAII-DASH干涉直条纹与CCD探测器以不同耦合角叠加时产生的莫尔条纹模拟结果
(a): 耦合角0° ; (b): 耦合角1° ; (c): 耦合角4° ; (d): 耦合角19° Fig.4 Simulation results of Moiré fringes produced by the superposition of GBAII-DASH interferometric straight fringes and CCD detector signals at different coupling angles
(a): 0° ; (b): 1° ; (c): 4° ; (d): 19°

为了研究莫尔条纹对测风精度的影响, 我们从模拟风速是10、 20、 30、 40和50 m· s^-1的含有莫尔条纹的干涉图中提取风速, 首先对干涉图进行平场处理, 我们这里的平场做法是选取出干涉图中多行值后求平均, 然后再用 “ 四强度法” 和傅里叶变换法从干涉图中提取风速。

以耦合角α =0° , 风速为v₁=50 m· s^-1为例, 对含有莫尔条纹的模拟干涉图进行处理, 提取出与风速相关的相位^[13]

$φ_{v} = 4 π σ_{0} Δ Lv / c$ (6)

其中2Δ L=Δ ₀=7.495 cm为GBAII-DASH系统的固定光程差, c为真空中光速, σ ₀为零风速的气辉波数。再根据我们提出的“ 四强度法” 测风, 得到一个周期范围内步进相位分别为0、 π /4、 2π /4和3π /4所对应的4个干涉强度值I₁、 I₂、 I₃和I₄, 利用表达式(7)的反正切^[13]

$\tan (φ_{0} + φ_{v}) = (I_{4} - I_{2}) / (I_{1} - I_{3})$ (7)

即可求出零风速相位φ ₀(对应固定光程差)和含风速的相位φ _v₌₅₀, 进而求出风速为v₂=48.55 m· s^-1, 风速误差Δ v=v₁-v₂=1.45 m· s^-1。同理我们用“ 四强度法” 分别求出耦合角α =1° 、 2° 、 3° 、 4° 、 9° 、 14° 和19° 情况下的反演风速值如表1所示。从表1结果可见, 测风相对误差的平均值约为3.07%。

表1 不同耦合角下基于“ 四强度法” 测风的结果 Table 1 Results of wind measurement at different coupling angles by the “ Four-point algorithm”

利用傅里叶变换法求风速, 即利用干涉强度

$\begin{array}{l} I_{D}^{0} (x) = S_{0} E_{0} (x) \exp [i (2 π κ_{0} x + φ_{0} + δ φ_{0})] / 2 \\ = S_{0} E_{0} (x) [\cos (2 π κ_{0} x + φ_{0} + δ φ_{0}) + \\ i \sin (2 π κ_{0} x + φ_{0} + δ φ_{0})] / 2 \end{array}$ (8)

的虚部sin和实部cos的反正切

$2 π κ_{0} x + φ_{0} + δ φ_{0} = \arctan [J (I_{D}^{0}) / R (I_{D}^{0})]$ (9)

获得CCD上不同位置点x处的相位所对应的风速。鉴于选择CCD的中心区域的光程差点来提取相位的计算结果较为准确, 故我们选取CCD上位于x=289像素位置求风速。以耦合角α =1° 时为例, 用傅里叶变换法分别从模拟风速v₁'=50 m· s^-1含有莫尔条纹的GBAII-DASH成像干涉徒中提取出相位。由式(8)和式(9)求出零风速相位和含有风速的相位, 再由式(6)求出风速为v'₂=54.46 m· s^-1, 风速误差Δ v'=v'₁-v'₂=4.46 m· s^-1。同理我们求出不同耦合角下的风速值如表2所示, 可见所有结果的测风相对误差的平均值约为6.89%。

表2 不同耦合角下基于傅里叶变换法测风的结果 Table 2 Results of wind measurement at different coupling angles by the Fourier transform method

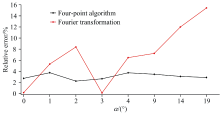
在相同耦合角α 下, 利用“ 四强度法” 和傅里叶变换法得到的测风误差结果如图5所示。由图5可知, 用“ 四强度法” 时, 不同耦合角度的莫尔条纹对测风精度的影响均较小, 测风误差约为3.00%; 而用傅里叶变换法时, 莫尔条纹的存在严重影响测风精度, 且耦合角度在14° 和19° 时, 测风误差大于10.00%, 再次说明用 “ 四强度法” 提取GBAII-DASH干涉图的大气风速比傅里叶变换法更具优势^[13]。

	Figure Option View Download New Window
	图5 有莫尔条纹时“ 四强度法” 和傅里叶变换法的测风相对误差与耦合角之间关系图Fig.5 The relationship between the relative error and coupling angle of wind measurings by “ Four-point algorithm” and Fourier transform method with Moiré fringes analysis

实际拍摄中, 图1所示的光学系统难免有操作误差, 干涉图与CCD光敏元件阵列的耦合角可能发生变化。下面我们分析不同风速和耦合角情况下, 莫尔条纹对测风精度的影响。

我们用“ 四强度法” 测风对耦合角为0° 、 1° 、 2° 、 3° 、 ···、 19° 且风速是10、 20、 30、 40和50 m· s^-1正演模拟GBAII-DASH系统的干涉图进行处理并提取风速的误差结果如图6所示, 结果可见, 测风相对误差的浮动范围很广, 最小为0.23%, 最大可达33.45%, 可见莫尔条纹的存在将严重影响干涉仪系统的测风精度。我们还正演模拟了零风速的不同耦合角时的干涉图, 用“ 四强度法” 从含有莫尔条纹的干涉图中提取风速, 并求出测风相对误差, 计算结果如表3所示。从表3可见, 总测风相对误差的平均值约为6.24%, 故可认为莫尔条纹对GBAII-DASH系统的测风精度的影响不可忽视。

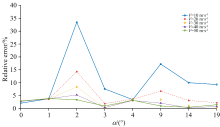	Figure Option View Download New Window
	图6 不同耦合角下“ 四强度法” 测风的相对误差结果Fig.6 The relative errors of wind measurement by the “ Four-point algorithm” at different coupling angles

表3 不同风速与不同耦合角时“ 四强度法” 的测风结果 Table 3 Wind measurement results of the “ Four-point algorithm” at different wind speeds and coupling angles

1.3 消除莫尔条纹提高GBAII-DASH测风精度

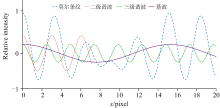
将莫尔条纹看成是各级谐波和基波的叠加^[15], 我们根据式(5)模拟得到莫尔条纹波函数的叠加如图7所示, 可见莫尔条纹波函数中基频项形成的莫尔条纹周期最大。为了消除GBAII-DASH干涉图中的莫尔条纹, 我们最主要是分辨出基频项所生成的莫尔条纹^[16]。将模拟的GBAII-DASH干涉图当成光栅1, CCD探测器光敏元件阵列当成光栅2。假设光栅1和光栅2的空间频率分别是k₁和k₂, 根据我们的实验器件参数知k₁=12.2 L· mm^-1, k₂=16.3 L· mm^-1。当两个光栅的耦合角为0° 时, 由式(2)分别求出光栅1和2的透过率函数T₁和T₂, 由式(3)求出叠加后的透过率函数T, 计算结果如图8所示。光栅组叠加后的透过率函数的基频项是与光栅的空间频率有关, 从图8可知, 透过率函数T的基频项易被分离(图中的红线是基频波), 故莫尔条纹容易被观察到。

	Figure Option View Download New Window
	图7 莫尔条纹波函数的合成Fig.7 Synthesis of the moiré fringe wave function

	Figure Option View Download New Window
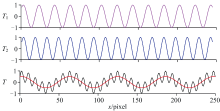	图8 较小空间频率差(k₁=12.2 L· mm^-1, k₂=16.3 L· mm^-1)的两光栅透过率函数Fig.8 Transmittance function of two gratings with a smaller spatial frequency difference(k₁=12.2 L· mm^-1, k₂=16.3 L· mm^-1)

当k₁=12.2 L· mm^-1, k₂=83.3 L· mm^-1时, 运用式(2)和式(3)求出此时光栅1、 2和两光栅叠加后的透过率函数如图9所示。由图9可知, 两光栅叠加后的透过率函数的基频项不能很好地分离出来, 故认为此时莫尔条纹不易被观察到, 也就是两光栅叠加后产生的莫尔条纹对干涉图的影响较小。

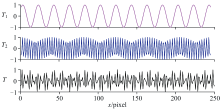	Figure Option View Download New Window
	图9 较大空间频率差(k₁=12.2 L· mm^-1, k₂=83.3 L· mm^-1)的两光栅透过率函数Fig.9 Transmittance function of two gratings with a larger spatial frequency difference(k₁=12.2 L· mm^-1, k₂=16.3 L· mm^-1)

我们得出结论: 当两光栅的k₁和k₂的差值Δ k=|k₁-k₂|≪min(k₁, k₂)时, 莫尔条纹容易被观察到, 且容易被分离出来; 当两光栅的k₁和k₂相差较大时, 莫尔条纹的信息不易被提取出来, 莫尔条纹现象不易被观察。综上可知: 我们可以通过改善GBAII-DASH干涉仪系统的器件使得中高层大气气辉谱线成像干涉图条纹的空间频率与CCD探测器像素阵列的空间频率的差值增大, 来减小莫尔条纹对测风精度的影响。具体方法有, 减小GBAII-DASH干涉仪系统中CCD探测器像素的尺寸, 或者提高GBAII-DASH系统的视场展宽, 增大成像干涉条纹的周期。

选用像素大小为12的CCD探测器, 对应k₂=83.3 L· mm^-1, 模拟该情况下不同耦合角和风速的含有莫尔条纹的干涉图, 用“ 四强度法” 从干涉图中提取风速, 当模拟干涉图零风速和含有风速的初始条件相同时, 测风误差是2.60%, 小于表1情况中3.07%的测风误差, 当模拟干涉图零风速和含有风速的初始条件不同时的测风误差结果如表4所示, 表4 中所列情况的平均值为4.12%, 小于表3的平均测风误差6.24%, 可见提高了测风精度。

表4 k₂=83.3 L· mm^-1时“ 四强度法” 的测风结果 Table 4 Wind measurement results of the “ Four-point algorithm” when k₂=83.3 L· mm^-1

鉴于中高层大气的气辉光强很弱, 又需要我们选用大尺寸像素的CCD探测器, 有时也会将2× 2的像素作为一个bin来接收气辉, 所以在设计干涉仪系统时, 要考虑到CCD探测器光敏元件的空间频率与气辉谱线干涉图的空间频率这两者的数量关系, 我们的“ 四强度法” 拉伸法可以进一步减少莫尔条纹现象的影响, 更合适提高测风精度的要求。

2 实验结果与讨论

通过上述理论和正演模拟结果, 我们建议在GBAII-DASH探测过程中, 尽可能匹配实验条件, 以消除莫尔条纹对测风精度的影响, 例如图10是用532 nm的激光作为光源在实验室零风速情况下实际拍摄的GBAII-DASH的成像干涉图结果, 图10(a)未见明显的莫尔条纹, 图10(b)中可见明显的横向莫尔条纹, 且干涉图的强度分布不均匀。图10的这两幅图的其他拍摄条件相同, 只是拍摄时微调了GBAII-DASH系统中一个闪耀光栅的摆放位置, 闪耀光栅的位置改变会导致干涉条纹整体发生旋转, 也就是耦合角的改变。模拟风速不同、耦合角不同时, 莫尔条纹对测风精度的影响均不同, 在实验室尽可能消除莫尔条纹的影响。

Figure Option
View Download New Window

图10 零风速时不同耦合角下室内GBAII-DASH的成像干涉图
(a): 初始成像干涉图; (b): 微调闪耀光栅后明显有莫尔条纹的干涉图Fig.10 Imaging interferograms of GBAII-DASH in the indoor environmentat different coupling angles at zero wind speed
(a): Initial imaging interferogram; (b): Interference pattern with obvious Moiré fringes after fine-tuning the blazed grating

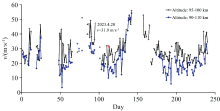
鉴于GBAII-DASH探测的室外光源是西安上空98 km处的O(¹S)557.7 nm气辉, 我们比较研究了GBAII-DASH与TIDI^[17]的观测结果如图11所示, 其中TIDI在2023.4.20探测西安上空的大气纬向风速为31.9 m· s^-1(高度范围是90~100 km), 2023.4.20我们把GBAII-DASH搬到距离西安市临潼山上的穹庐民宿(海拔1 250 m, 34.3° N, 109.3° E), 用“ 四强度法” 反演处理观测到的干涉图, 得到的风速结果为32.2 m· s^-1, 两者误差0.3 m· s^-1。可见消除莫尔条纹后采用“ 四强度法” 确实大大提高了GBAII-DASH的测风精度。

	Figure Option View Download New Window
	图11 2023年1月— 8月TIDI探测西安上空90~100 km的大气风速 * 为GBAII-DASH在2023.4.20日的探测结果Fig.11 Upper atmospheric wind speed over Xi′an at the altitude of 90~100 km detected by TIDI from January to August in 2023 * The detection result of GBAII-DASH on April 20, 2023

3 结论

研究了GBAII-DASH系统中莫尔条纹的成因及其对测风精度的影响, 并提出了改善莫尔条纹的方法以提高测风精度。因GBAII-DASH系统获得的干涉条纹是明暗相间的直条纹, 它以一定耦合角成像到CCD的面阵结构上时, 将可能出现莫尔条纹。得到如下结论:

(1)本文理论分析了系统中莫尔条纹的数学模型, 模拟分析了不同耦合角情况下形成的含莫尔条纹的干涉图, 发现了纵向和横向两种类型的莫尔条纹。

(2)用“ 四强度法” 和傅里叶变换法两种测风方法从干涉图反演风速, 研究了零风速耦合角与有风速耦合角相同和不同两种情况下莫尔条纹对测风精度的影响, 发现莫尔条纹对系统测风精度是有影响的, 且“ 四强度法” 反演风速的误差较小。

(3)通过频谱分析方法模拟研究发现: 增大中高层大气气辉谱线成像干涉图条纹的空间频率与CCD探测器像素阵列的空间频率的差值可以改善GBAII-DASH系统莫尔条纹对测风精度的影响。

(4)给出了不同实验条件下得到的莫尔条纹明显与否的两种干涉条纹, 并于2023.4.20在室外搭建GBAII-DASH系统进行探测, 利用“ 四强度法” 从探测的结果反演风速并与TIDI观测的数据进行了比较, 发现减少了莫尔条纹之后用“ 四强度法” 测风的误差很小。

参考文献

文献列表

[1]	Hays P B, Abreu V J, Dobbs M E, et al. Journal of Geophysical Research: Atmospheres, 1993, 98(D6): 10713. [本文引用:2]
[2]	Shepherd G G, Thuillier G, Gault W A, et al. Journal of Geophysical Research: Atmospheres, 1993, 98(D6): 10725. [本文引用:1]
[3]	McLand ress C, Shepherd G G, Solheim B H, et al. Journal of Geophysical Research: Atmospheres, 1996, 101(D6): 10441. [本文引用:1]
[4]	Killeen T L, Wu Q, Solomon S C, et al. Journal of Geophysical Research: Space Physics, 2006, 111(a10): A10S01-1. [本文引用:1]
[5]	LI Jin-hua, ZHANG Min-juan, WANG Zhi-bin, et al(李晋华, 张敏娟, 王志斌, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(6): 1974. [本文引用:1]
[6]	Englert C R, Harland er J M, Marr K D, et al. Space Science Reviews, 2023, 219(3): 27. [本文引用:2]
[7]	Englert C R, Harland er J M, Babcock D D, et al. Proceedings of SPIE, 2006, 6303: 63030T. [本文引用:2]
[8]	PENG Xiang, LIU En-hai, TIAN Shu-lin, et al(彭翔, 刘恩海, 田书林, 等). Acta Physica Sinica(物理学报), 2022, 71(24): 240601. [本文引用:1]
[9]	Gao H Y, Tang Y H, Hua D X, et al. Applied Optics, 2013, 52(36): 8650. [本文引用:1]
[10]	Tang Y H, Duan X D, Gao H Y, et al. Applied Optics, 2014, 53(11): 2273. [本文引用:1]
[11]	Tang Y H, Yang R, Gao H Y, et al. Proceedings of SPIE, 2017, 10256: 102563C. [本文引用:1]
[12]	FANG Yan, LI Cun-xia, HUI Ning-ju, et al(方妍, 李存霞, 惠宁菊, 等). Chinese Journal of Geophysics(地球物理学报), 2024, 67(3): 960. [本文引用:1]
[13]	LI Wen-wen, HUI Ning-ju, LI Cun-xia, et al(李文文, 惠宁菊, 李存霞, 等). Acta Physica Sinica(物理学报), 2023, 72(24): 240601. [本文引用:4]
[14]	Savelje V V, Son J-Y, Javidi B, et al. Journal of Display Technology, 2005, 1(2): 347. [本文引用:1]
[15]	Savelje V V, Kim S-K. Optics Express, 2013, 21(2): 1693. [本文引用:1]
[16]	WANG Xue-li, LI Gen-qian, ZHAO Hong, et al(王学礼, 李根乾, 赵宏, 等). Semiconductor Optoelectronics(半导体光电), 2001, 22(1): 65. [本文引用:1]
[17]	TIDI: TIMED Doppler Interferometer TIMED Instrument: http://tidi.engin.umich.edu. Michigan Engineering, 2025. [本文引用:1]

1993

0.0

... s^-1[1] ...

1993

0.0

... s^-1[2], WINDII和HRDI相互重叠30 km大气区域相互验证的探测结果证明FPI和MI两种仪器均具优良品质^[3] ...

1996

0.0

... s^-1[2], WINDII和HRDI相互重叠30 km大气区域相互验证的探测结果证明FPI和MI两种仪器均具优良品质^[3] ...

2006

0.0

... s^-1[4] ...

2022

0.0

... 为了提高仪器分辨率^[5]、稳定性和测风精度, 2019年搭载在Ionospheric connection explorer(ICON)卫星上的Michelson Interferometer for Global High-resolution Thermospheric Imaging(MIGHTI)^[6]探测90~300 km的大气风速, MIGHTI采用Doppler Asymmetric Spatial Heterodyne Spectroscopy(DASH)^[7]思路, 将广角MI两臂的反射镜替换为闪耀光栅实现静态测风, DASH采用傅里叶变换法探测高层大气风速^[7], MIGHTI的测风精度达1 ...

2023

0.0

... s^-1[6] ...

2006

0.0

2022

0.0

... 0%以内^[8] ...

2013

0.0

... 2012年, 我们课题组研制了地基气辉成像干涉仪(Ground Based Airglow Imaging Interferometer, GBAII), 将广角MI和窄带FPI揉合在一起的GBAII成功探测了西安上空90~100 km的大气风速、温度、体发射率、重力波等物理量^[9,10,11,12], 探测目标光源是峰值高度为94 km的O₂(0-1) 865 ...

2014

0.0

2017

0.0

2024

0.0

2023

0.0

... 测风, 它与目前国际上流行的DASH傅里叶变换法测风相比具有更高精度^[13] ...

... s^-1为例, 对含有莫尔条纹的模拟干涉图进行处理, 提取出与风速相关的相位^[13] ...

... /4所对应的4个干涉强度值I₁、 I₂、 I₃和I₄, 利用表达式(7)的反正切^[13] ...

... 提取GBAII-DASH干涉图的大气风速比傅里叶变换法更具优势^[13] ...

2005

0.0

... 我们根据参数文献[14]的思路, 进行坐标旋转后, 得到透过率式(5)中的5个波数: #cod#x0221e ...

2013

0.0

... 3 消除莫尔条纹提高GBAII-DASH测风精度将莫尔条纹看成是各级谐波和基波的叠加^[15], 我们根据式(5)模拟得到莫尔条纹波函数的叠加如图7所示, 可见莫尔条纹波函数中基频项形成的莫尔条纹周期最大 ...

2001

0.0

... 为了消除GBAII-DASH干涉图中的莫尔条纹, 我们最主要是分辨出基频项所生成的莫尔条纹^[16] ...

2025

0.0

... 7 nm气辉, 我们比较研究了GBAII-DASH与TIDI^[17]的观测结果如图11所示, 其中TIDI在2023 ...