引用本文
张贺, 高昆, 柯坤鑫, 王敬宜, 张泽丰, 胡柏杨, 杨纪元, 程灏波. 基于多级循环优化网络的复杂光照高光谱反射率无参重建方法[J]. 光谱学与光谱分析, 2025,45(8): 2174-2182.
ZHANG He, GAO Kun, KE Kun-xin, WANG Jing-yi, ZHANG Ze-feng, HU Bai-yang, YANG Ji-yuan, CHENG Hao-bo. Reference-Free Reconstruction of Hyperspectral Reflectance Under Complex Illumination Based on Multi-Level Cyclic Optimization Network[J]. Spectroscopy and Spectral Analysis, 2025,45(8): 2174-2182.
Doi:10.3964/j.issn.1000-0593(2025)08-2174-09  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于多级循环优化网络的复杂光照高光谱反射率无参重建方法
张贺, 高昆*, 柯坤鑫, 王敬宜, 张泽丰, 胡柏杨, 杨纪元, 程灏波
近地面探测全国重点实验室, 北京 100072
*通讯作者 e-mail: gaokun@bit.edu.cn

作者简介: 张 贺, 女, 2002年生, 北京理工大学光电学院硕士研究生 e-mail: zhanghe819925@163.com

收稿日期: 2024-12-25 修回日期: 2025-04-08
基金: 国家自然科学基金项目(U2241275)资助
摘要

光谱反射率重建旨在从高光谱图像中计算得到物体表面对入射光的真实反射率分布情况, 是定量遥感等高光谱成像应用领域中研究的重要内容。 传统的反射率重建方法主要依赖于统计学模型, 往往需要稳定的平场光照条件或参考图像等先验信息来进行反射率估计。 然而, 在实际应用中如果缺乏参考图像等先验信息, 尤其是当光照条件复杂多变的情况下, 利用传统方法重建的精度并不理想。 针对这一问题, 将光照估计和反射率重建视为一个约束矩阵的分解问题, 提出了一种用于光谱反射率重建的多级循环优化网络模型。 该模型通过通道-空间混合注意力机制, 自适应聚焦反射光谱图像的关键特征, 强化非均匀、 多光源光照条件下关键信息的提取与增强, 提升重建鲁棒性。 同时, 通过联合引入低秩化与全变分正则化模块构建去噪机制: 低秩正则化挖掘光照与反射率的潜在低维结构, 抑制噪声干扰; 全变分正则化则沿空间维度施加平滑约束, 在提高重建精度的同时减少光谱突变与冗余信息, 保障空间一致性。 为了验证所提出方法的有效性, 设计了相关的数据预处理、 模型训练和评估方法。 在训练过程中以KAUST高光谱数据集为训练集, 测试中模拟添加了不同类型的入射光源场景, 并以CIE 1964 10°标准观察者色彩匹配函数为基准, 将高光谱图像转化为彩色图像进行可视化展示和性能的定量化评价。 实验结果表明, 所提出无参考反射率重建方法较传统统计类的重建方法和当前流行的深度学习类重建方法, 在SAM、 GFC等重建精度指标上更具优势; 尤其在无定标白板作为参考的情况下, 仍能保证光谱重建的精度, 显示出本论文方法在复杂光照环境下具有更好的泛化能力和良好的重建精度。

关键词: 光谱反射率; 多级循环优化; 混合注意力机制; 无参重建
中图分类号:O433.4 文献标志码:A
Reference-Free Reconstruction of Hyperspectral Reflectance Under Complex Illumination Based on Multi-Level Cyclic Optimization Network
ZHANG He, GAO Kun*, KE Kun-xin, WANG Jing-yi, ZHANG Ze-feng, HU Bai-yang, YANG Ji-yuan, CHENG Hao-bo
National Key Laboratory on Near-surface Detection, Beijing 100072, China
*Corresponding author
Abstract

Spectral reflectance reconstruction aims to calculate the true reflectance distribution of an object's surface in response to incident light from hyperspectral images. It is an important research topic in quantitative remote sensing and other hyperspectral imaging applications. Traditional reflectance reconstruction methods mainly rely on statistical models, often requiring stable flat-field illumination conditions or reference images as prior information for reflectance estimation. However, when reference images or other prior information are lacking in practical applications, especially under complex and varying lighting conditions, reconstruction accuracy using traditional methods is not ideal. This paper treats illumination estimation and reflectance reconstruction as a constrained matrix decomposition problem to address this issue. It proposes a multi-level cyclic optimization network model for spectral reflectance reconstruction. The model utilizes a hybrid channel-spatial attention mechanism to adaptively focus on key features in reflectance spectral images, thereby enhancing the extraction and amplification of critical information under non-uniform and multi-illuminant conditions, significantly improving reflectance reconstruction's robustness. Additionally, the network integrates a denoising mechanism comprising two modules: low-rank regularization and total variation regularization. The low-rank regularization module explores the intrinsic low-dimensional structures of illumination and reflectance to suppress noise interference. The total variation regularization module imposes spatial smoothness constraints on the reconstructed spectra, thereby improving reconstruction accuracy, reducing spectral mutations and redundant information, and ensuring spatial consistency throughout the process. To validate the effectiveness of the proposed method, this paper designs related data preprocessing, model training, and evaluation methods. The KAUST hyperspectral dataset is used as the training set in the training process, and different types of incident light source scenarios are simulated in the testing phase. Using the CIE 1964 10° standard observer color matching function as a reference, the hyperspectral images are converted into color images for visualization and quantitative performance evaluation. Experimental results show that the proposed reference-free reflectance reconstruction method outperforms traditional statistical-based reconstruction methods and current popular deep learning-based reconstruction methods regarding reconstruction accuracy indicators such as SAM and GFC. Particularly, without a calibrated whiteboard as a reference, the method still maintains high spectral reconstruction accuracy, demonstrating superior generalization capability and excellent reconstruction performance in complex lighting environments.

Keyword: Spectral reflectance; Multi-level cyclic optimization; Hybrid attention mechanism; Reference-free reconstruction
0. 引言

光在物体表面发生反射时, 会呈现出多种复杂的反射机制。 如体反射、 表面反射和次表面散射等, 它们共同作用呈现了物体的视觉特性然后被光谱相机捕获。 除了物体表面复杂的反射机制, 入射到物体表面的光源的数量及种类也是难以确定的, 这导致物体表面呈现的反射光谱复杂多样, 难以利用统一的物理模型进行描述。 光谱反射率是物体的固有信息, 不会随照明条件的改变而改变, 基于光谱反射率进行目标识别或分类能有效克服同色异谱问题, 因此光谱反射率的重建被广泛应用在安防识别[1, 2]、 材质筛选[3]、 植被反演[4]等领域。

在高光谱成像过程中, 图像中每个像素的响应由照明光源的光谱分布、 物体表面的光谱反射特性以及相机的光谱响应共同作用。 通过使用Hadamard乘积来表示照明光谱与反射率光谱的乘积, 可以有效地将每个像素的观测值分解为照明和反射的贡献。 因此, 复杂光照条件下光谱反射率的无参重建问题的核心在于精确估计每个像素的光照光谱(即受环境光照影响的光谱)以及与光照无关的物体表面反射率光谱。 一般来说, 光谱反射率重建方法主要可以分为以下三类: 基于图像统计先验的方法、 基于场景物理约束的方法和基于光谱数据驱动的深度学习方法。 这一分类框架已被广泛接受, 并在多光源估计与动态场景重建中得到验证[5]。

基于图像统计先验的方法通过捕获场景的统计特性并设定假设先验来估计照明光谱, 往往需要较为理想的光照条件, 如Gray World[6]假设认为照明光谱可以直接从整个图像的平均响应中获得, 难以应对多光源或非均匀照明的复杂环境, 且对反射率和光源光谱的重建精度有限。 Wang等[7]基于统计规律寻找最佳光谱分布, 通过优化光源的光谱分布来提升光谱反射率的重建精度。 基于图像统计先验的方法主要依赖场景内的统计规律和归一化方法, 适合在有部分参考区域或特定光源条件下使用, 但其对非均匀照明的敏感性仍需依赖颜色幻觉等生物学机制进行补偿[8]。

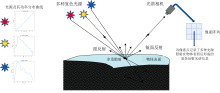图1 光在物体表面的反射机制及被高光谱相机捕获Fig.1 The reflection mechanism of light on the surface of an object and a hyperspectral camera capturing light

基于场景物理特性约束的重建方法通过物理模型训练样本, 建立成像系统响应值与光谱反射率之间的学习映射关系, 早期依赖引导滤波[9]、 维纳估计[10]等传统模型, 此类模型受限于定标白板对光学系统的校正和光谱反射率真值的获取。 近年来, 研究人员提出联合分割与单光源估计的框架, 通过学习模型实现多光源场景下的区域分割与局部光源估计, 显著提升了物理约束方法的适用性[11]。 基于场景物理约束的方法强调物理建模和优化求解, 但局限于光源和传感器特性已知、 且物理规律可以准确建模的场景。

基于光谱数据驱动的深度学习方法通过训练数据的映射能力应对复杂环境, 具有更广泛的学习性和特征提取能力[12]。 早期研究主要通过改进网络架构提升性能: 基于CIFARIO-quick网络[13]的方案虽然利用多尺度输入来预测光源, 但在单一卷积结构的局限下, 难以全面关注关键的光谱特征; IGTN网络[14]则通过深度度量学习提升了光源一致性, 但仍需依赖特定模块对光源进行分类, 缺乏适应性; 三阶段卷积神经网络[15]图像估计方法采用逐阶段局部和全局估计来细化光源, 但流程复杂且对场景变化敏感, 难以处理多变的环境。 最新研究提出亮度鲁棒性增强策略, 通过对抗性亮度增强与对比损失优化, 显著提升了深度模型对亮度变化的适应能力[16]; 此外, 基于双曝光特征的模型设计可有效利用多帧信息提升光源估计精度[17]。 基于光谱数据驱动的深度学习方法融合对抗学习、 多模态感知与高效架构设计, 正逐步突破复杂光照的固有限制, 但其对标注数据的强依赖性仍是开放场景应用的瓶颈[18]。

传统白板定标类方法的核心缺陷在于: 其假设“ 标定区域的光照代表全局光照” , 而这一假设在非均匀、 多光源场景中严重失效。 而且在高光谱数据采集的过程中, 并不是所有场景都具备白板定标与校准的条件, 且一般自然场景下的照明环境通常较为复杂, 光源的数量、 光强的空间分布以及光源的入射角度都难以确定[19]。 此外, 高光谱图像中每个波段都包含丰富的场景信息, 相邻波段之间的高相关性往往带来冗余数据, 增加了模型处理的难度。

本工作旨在解决在复杂环境光照条件下, 如何自适应地聚焦于关键光谱区域并克服无定标板限制, 准确重建开放场景中的高光谱图像光谱反射率。 为此, 提出了一种基于多级循环优化网络的复杂光照下的高光谱反射率无参重建方法。 通过引入混合注意力机制[20], 模型能够自动聚焦于光谱反射率中的重要特征, 提高在不同光照条件下的鲁棒性, 并有效抑制背景噪声干扰。 通过动态调整不同场景下的光谱权重, 模型能够实现更精确的光谱反射率重建, 从而增强在复杂光照环境中的适应能力。 此外, 该方法实现了无定标下的光谱反射率重建, 能够在开放场景中获取任意像素点的光谱反射率, 避免了光谱相机使用中的定标板放置限制的问题。

1 原理
1.1 复杂光照下的高光谱反射率重建方法框架

针对复杂照明条件与反射机制下捕获的高光谱图像, 开展了像素级的照明光谱与光谱反射率重建的研究。 当波长λ 在400~1 000 nm范围内变化时, 一个像素点或样本在相机的第i通道所得到的响应可以被表示为

Ii=∫400nm1000nmL(λ)R(λ)C(λ)dλ+ni(1)

式(1)中, L(λ )为照明光源的光谱功率分布, R(λ )表示物体表面的光谱反射特性, C(λ )描述了相机的光谱响应[21]。 在高光谱成像中, 图像被表示为一个二维mn× c矩阵, 旨在将每个像素分解为照明光谱L和反射率光谱R的乘积, 且L和R的维度也为m× n× c。 每个像素值由L和R的Hadamard乘积并加上噪声或者误差项表示。 在单照明估计的情况下, 照明光谱向量L被视为所有像素共享相同光谱的一阶矩阵。 而在多重照明估计的情况下, 则需要逐像素重建照明光谱和反射率。

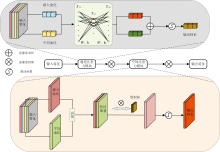
本工作提出的像素级高光谱反射率重建网络如图2所示, 主要由不均匀照明高光谱图像的合成、 混合注意力机制和多级循环优化网络展开三个模块组成, 以应对复杂光照条件下的光源估计和反射率重建。 通道和空间注意力机制分别在光谱通道和空间区域内聚焦关键特征, 优化网络则基于多个循环阶段逐步更新关键变量, 包括反射率R、 照明光谱L、 非局部先验、 全变分正则化项和一系列相应的辅助变量等。 该方法将光源和反射率重建视为矩阵分解问题, 引入稀疏性和光照平滑性正则化, 并在测试时无须依赖白板定标真值, 确保模型在多变照明场景下的稳健性与重建精度。

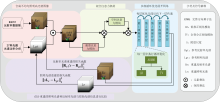图2 复杂场景下的高光谱反射率重建方法框架Fig.2 A framework for hyperspectral reflectance reconstruction in complex scenarios

本方法将光照估计和反射率的重建视为约束矩阵的分解, 用优化问题可以描述为

minR, L‖I-R☉L‖F2+α|R|1+β‖L‖TV, subject to:L≥0, R≥0, ∑i=1mLi=1(2)

式(2)中, α |R|1是反射率的稀疏性正则化, 鼓励反射率矩阵R的稀疏性, 因为在一幅图像上反射率矩阵R的很多像素点是暗的, 只有少数连续区域会有较高的反射率, 该非局部先验可以帮助优化器更快找到符合该特性的解, 并减少不必要的噪声。 β ‖ L‖ TV是照明光谱的全变分正则化项, 用于在空间维度上平滑照明, 相邻像素的光照值也是趋向一致的, 进而保持在图像边缘减少不必要的波动。 使用非局部正则化项进行反射率重建考虑了非局部数据冗余。

除此之外, 考虑物理合理性, 估计的光谱照度被限制为非负值并做归一化约束, 反射率R被限制在[0, 1]范围内。

1.2 混合注意力机制

通道注意力机制模块用于在通道维度上增强关键光谱特征的表达。 该模块首先对输入特征图进行全局最大池化和全局平均池化, 从而在空间维度上压缩特征图, 获得两张通道特征描述。 池化后的两张特征图共用一个多层感知器网络, 该网络包括两个全连接层: 第一个全连接层将通道数从c降至较小的维度c/r, 第二个全连接层则将通道数恢复至原始维度c。 得到的特征图在通道维度上相加后通过激活函数Sigmoid, 将每个通道的权重归一化到[0, 1]区间。 最后, 将归一化后的权重与输入特征图逐元素相乘, 得到通道注意力加权后的输出特征图。

空间注意力机制模块用于在空间域处理通道注意力机制输出的特征图。 具体而言, 该模块首先对输入特征图在通道维度上执行最大池化和平均池化操作。 将这两张特征图在通道维度上堆叠, 得到堆叠特征, 然后使用一个大小为7× 7的卷积核对堆叠后的特征图进行卷积, 以融合通道信息并压缩至单通道特征图。 最后, 将输入特征图与空间权重逐元素相乘, 从而得到空间注意力加权后的输出。

通过该机制, 模型可以更加专注于光谱反射率重建过程中对重建结果有显著影响的光谱和空间区域, 从而提升重建的准确性。

1.3 算法伪代码

本算法伪代码如下:

算法1 基于多级循环优化网络的高光谱反射率无参重建算法

输入: 真实光谱反射率: Rgt, 照明光谱: Lgt

光谱重建注意力网络fsra, 非线性重构映射frec

输出: 重建后的光谱反射率Re和照明光谱Le

a.混合注意力机制权重

1. 初始化网络fsra并根据光谱波段信息构建波段编码图像X'a

2. 通道注意力模块: 生成通道注意力权重矩阵Wchannel, 从而在通道维度上聚焦于关键光谱特征

3. 空间注意力模块: 生成空间注意力权重矩阵Wspatial, 聚焦图像中的重要空间区域, 提升光谱重建的空间一致性

4. 光谱特征提取与重构: 利用重构映射网络frec对经过通道和空间注意力处理后的数据X'a提取光谱特征, 并重构得到原始光谱Xa

5. 迭代优化更新: 利用多级循环优化展开网络, 通过迭代更新对偶变量, 实现对反射率Rgt和照明Lgt的注意力增强和特征优化

6. 优化权重矩阵: 通过最小化损失函数, 优化frec和fsra的参数, 得到最终的目标注意力权重矩阵Wsra

b. 多级循环优化展开网络:

1. 分层处理: 初始化每一层的展开网络, 利用交替方向乘子法 (alternating direction method of multipliers, ADMM)将目标优化问题分解为多个子问题, 以实现反射率和照明光谱的精细优化

2. 特征更新: 在每层迭代执行低秩正则化(low rank, LR)和全变分正则化(total variation, TV)操作, 增强反射率和光谱估计的准确性

3. 重复更新: 重复步骤1— 2, 逐层展开优化直至达到预定的层数, 输出最终的反射率Re和Le

所提出的算法模型利用低秩正则化模块提取光照和反射率的潜在物理结构(如光源光谱平滑性、 反射率局部相似性), 替代白板的标定作用; 通过混合注意力模块动态分配光谱与空间权重, 在无参考区域的情况下精准定位关键特征(如高反射率区域), 避免传统方法对白板区域的依赖性。

图3 混合注意力机制进行特征提取流程Fig.3 The process of feature extraction using a hybrid attention mechanism

2 实验部分
2.1 高光谱图像反射率数据

为了测试所提出的算法在反射率重建方面的有效性, 使用有已知定标白板校正的KAUST高光谱数据集[22]。 该数据集共有400张光谱数据, 使用紧凑型扫描型高光谱相机Specim IQ获取。 为了得到真实反射率数据, 使用参考白板来计算高光谱图像上每个像素的反射光谱, 并将400~700 nm可见光范围内的光谱按10 nm间隔均匀采样, 总共31个通道。 裁剪图像大小为256× 256以去除参考定标白板, 保留高光谱图像场景主体部分, 并在[0, 1]范围内对高光谱反射率进行归一化。 最后随机选择320张图像来生成训练集, 并在其余80张图像上测试深度展开网络的性能, 每套都有数量均衡的室内/室外场景, 如图4所示。

图4 高光谱图像反射率数据集Fig.4 The image in hyperspectral reflectance dataset

2.2 复杂照明条件设计

为了合成各种模拟照明下的高光谱图像, 我们收集了一些常见标准光源的光谱功率分布数据来构建光谱照明数据集, 其中主要包括A光源、 D65光源、 C光源、 D50光源、 D55光源和D75光源等, 光源功率分布曲线如图5。

图5 光源功率分布曲线Fig.5 Power distribution curves of light sources

在单照明估计的情况下, 一般直接将单照明光源的SPD乘以反射图像来模拟捕获的高光谱图像。 但是实际场景下, 环境中往往存在多个照明光源且光强分布在空间上不均匀。 因此我们主要采用多重照明估计, 首先从照明数据集中随机选择三个照明光谱ω i (i=1, 2, 3), 然后生成三个随机的基于二维正弦的函数ω i(x, y)用于表示每个照明的空间分布。 随机空间分布函数表示每个光照的贡献, 定义为

ωi(x, y)=Aisin[ωi1(x+pi1)]sin[ωi2(y+pi2)][ωi1(x+pi1)][ωi2(y+pi2)](3)

式(3)中, A, ω , p分别是振幅、 频率、 相位。 将空间分布函数ω i归一化并保证各个贡献之和为常数, 这里令归一化函数之和 ∑ωi(i=1, 2, 3)=1, 确保整个功率分布曲线符合实际光源的性质。 空间变化照明是由三个照明光谱的线性组合生成的, 这种光谱照明的合成能够更好地模拟真实世界中的光照条件。

通过对非均匀、 多光源复杂照明场景的设计, 本方法通过式(3)生成的随机三个光源空间分布模型, 直接建模复杂光照的非均匀性和混合性, 无需白板提供光照先验, 摆脱了对白板的依赖。

2.3 训练过程

网络训练过程在NVIDIA GeForce RTX 3090上进行, 使用Pytorch构建模型。

之前的大多数方法都使用光谱的余弦相似度损失来训练或评估其模型, 然而这种损失函数对低强度像素中的图像噪声很敏感。 为了确保所提出方法的鲁棒性并迫使估计的反射率满足实际反射率的先验, 我们选择缩放估计照明和反射率的均方误差的加权组合作为损失函数, 表示为

L=‖sLe-Lgt‖22+ϕ1Res-Rgt22+ϕ2|log(s)|s=< Lgt, Le> < Le, Le> (4)

式(4)中, s表示照度尺度, ϕ 1和ϕ 2表示加权参数, Lgt、 Rgt和Le、 Re分别表示照明光谱及反射率光谱的真值和估计重建的照明光谱及反射率光谱, s应尽可能接近1, 以增强网络的鲁棒性并避免一般解。

3 结果与讨论
3.1 算法对比与结果展示

为了展示反射率光谱与随机照明合成的高光谱场景图像及照明估计的效果, 我们通过CIE 1964 10° 标准观察者色彩匹配函数将高光谱图像转化为RGB 图像。 首先获取D65光源的光谱功率分布并与图像数据进行逐像素相乘来实现模拟在D65标准光源下的图像数据, 然后根据高光谱图像数据S(λ )和色彩匹配函数, 通过数值积分计算XYZ值, 再将计算得到的XYZ值转换为RGB值。 转换得到的RGB值同样被限制在非负值并进行归一化表示, 使得最大RGB值为1, 从而确保图像在显示设备上的颜色真实呈现。

将对RGB三通道的颜色恒常性处理方法: Gray World、 Max-RGB扩展到31通道合成高光谱图像, 可重建出高光谱条件下经由经典颜色恒常性处理方法下的照明光谱及反射率。 Bianco等[23]使用卷积神经网络将特征学习和回归集成到一个回归过程中, FC4网络[24]利用不同置信度权重来处理具有估计模糊性的图像块, PWCC方法[25]使用基于U-Net的端到端训练框架, 通过双边滤波实现光照平滑, 最终实现像素级颜色恒常性校正。 为了量化估计的反射率重建精度, 我们采用RMSE、 SAM、 GFC这三个评价指标与上面的方法进行对比。 其中RMSE直接量化反射率曲线在数值上的全局偏差, 能够反映重建结果与真实光谱的绝对误差分布, 是评估光谱保真度的基础指标; SAM衡量重建光谱与真实光谱在形状和趋势上的相似性, 对区分不同物质的反射特性至关重要; GFC关注光谱曲线的局部梯度变化, 用于评估重建结果在细节特征(如吸收峰、 反射谷)的保留能力。

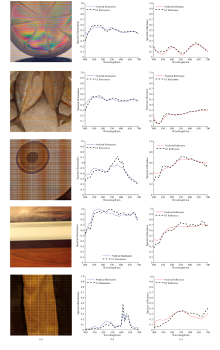
表1中的定量结果表明, 我们的方法在反射率重建的RMSE、 SAM和GFC三个指标上均优于其他方法, 尤其在GFC指标上达到了0.939 3, 显示了优异的光谱相关性。 与其他方法相比, 注意力机制引导的多级循环优化展开网络在重建反射率时能更好地捕捉高光谱图像中的复杂空间和光谱特征, 提高了模型在高光谱数据上的表现。 重建效果如图6所示。

表1 六种方法的反射率重建结果对比 Table 1 Comparison of reflectance reconstruction results using six methods

图6 各种照明场景下的真实和估计的照明光谱和反射率重建结果展示
(a): 合成高光谱图像; (b): 照明光谱估计重建结果; (c): 反射率估计重建结果Fig.6 Presentation of the actual and estimated illumination spectra and reflectance reconstruction results under various lighting scenarios
(a): Synthesized hyperspectral image; (b): Spectral reconstruction of illumination estimation; (c): Spectral reconstruction of reflectance

从图6中可以看出, 在多种照明条件下, 本方法能够很好地重建出接近真实的光谱曲线, 表现出较强的泛化能力和重建准确性, 无论是在高饱和度或复杂光源下, 都表现出较强的适应性和稳定性。

3.2 消融实验

为了充分研究展开混合注意力机制的代表模型、 卷积注意力模块(convolutional block attention module, CBAM)和去噪模块(LR: 低秩, TV: 全变分)的贡献, 进行了三次消融模拟实验, 以评价数据集上的多重照明条件下的重建效果。 定量结果如表2所示。

表2 消融实验结果展示 Table 2 Presentation of ablation experiment results

从定量显示结果可以看出, 对于照明光谱, 循环展开网络中的低秩化处理能够有效减少数据的冗余性和噪声, 从而提高图像的整体质量和清晰度; TV正则化处理则在空间维度上帮助保持图像的边缘细节和结构, 同时抑制噪声, 提升图像的对比度。 而引入混合注意力机制后, 模型在捕获多尺度特征和重要区域的权重分配方面展现出显著优势。 通过整合通道和空间注意力, 模型能够更好地关注信息丰富的区域, 从而增强对复杂光谱特征的学习能力。 对于反射率光谱的重建, 移除LR和TV模块后, 模型结构变得更简单, 这说明在特定的数据集或场景下, 模型可能更容易学习和适应原始数据的主要特征, 而不被噪声或非必要的细节干扰, 这导致了均方根误差的降低。 然而, 引入混合注意力机制后, 即便在复杂的光谱场景下, 光谱角映射和拟合优度仍然表现良好, 表明混合注意力机制在提升模型鲁棒性和提高重建效果方面发挥了关键作用。

此外, 在反射率光谱重建针对GFC这一指标的定量效果上, 在未使用CBAM的情况下, GFC值下降并不明显, 主要原因在于循环展开网络本身具备多尺度特征融合能力, 即使未引入注意力机制, 仍可通过卷积层捕捉一定程度的局部特征。 然而, CBAM的缺失导致模型对关键光谱区域的动态聚焦能力下降(例如高反射率波段或噪声敏感区域), 这直接反映在SAM指标的大幅劣化上, 表明光谱整体形状的保真度显著降低。 而移除TV模块时, GFC从0.933 1下降至0.650 1, 降幅显著, 这是因为TV模块对局部梯度细节的保持起到关键作用, GFC重点关注的就是光谱反射率曲线的局部梯度变化(如吸收峰、 反射谷的细节特征)。

综合三个指标在消融实验结果的表现来看, LR模块通过低秩先验增强了模型对光照和反射率中隐含物理结构的建模能力, 尽管在某些简单场景中移除LR后因拟合含噪数据可能降低RMSE, 但会严重损害光谱的物理合理性与泛化性; TV模块对局部梯度细节的保持起到关键作用(通过GFC指标体现); CBAM模块更侧重于优化光谱的全局形态相似性(通过SAM指标体现)。

4 结论

提出了一种基于混合注意力机制引导的多级循环优化网络, 用于复杂光照条件下的高光谱反射率重建。 实验结果表明, 与传统方法及主流深度学习模型相比, 本方法在多项关键指标上均取得显著提升。 相较于最优传统方法和深度学习基线, 本方法将RMSE误差分别降低22.5%(0.059 5 vs. 0.076 8)和12.6%(0.059 5 vs. 0.068 1), 验证了其在数值精度上的绝对优势; 且GFC拟合优度系数达到0.939 3, 远高于传统统计方法和基于物理模型的方法; SAM误差仅为1.996 7, 证明模型能够更精确地恢复光谱曲线的全局形态特征。 本模型的优势在于能够有效整合混合注意力机制对关键光谱和空间区域的捕捉和多级循环优化网络对相关变量的迭代更新, 进而克服复杂环境的干扰, 提高光谱反射率重建精度并显著减少估计误差, 并且不依赖于标准定标板提供的真值, 使得该方法在高光谱反射率重建领域具有较高的实用价值。

未来在农业遥感和生态环境监测领域, 该方法可摆脱传统标定白板的场地限制, 通过实时反演作物光谱特征实现精准长势监测, 或基于污染物光谱指纹实现野外环境的快速精准检测[26]; 在工业制造场景中, 其抗复杂光照干扰的特性可显著提升材料表面缺陷检测的稳定性, 为智能制造中的在线光谱质检提供可靠技术支撑[27]。 这种无需标定、 场景自适应的技术特性, 使得本方法在动态化、 多样式高光谱采集系统中具有独特的应用潜力。

参考文献
[1] Dib A, Thebault C, Ahn J, et al. Towards High Fidelity Monocular Face Reconstruction with Rich Reflectance Using Self-Supervised Learning and Ray Tracing, Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021: 12819. [本文引用:1]
[2] Ren X, Deng J, Cheng Y, et al. Monocular Identity-Conditioned Facial Reflectance Reconstruction. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2024: 885. [本文引用:1]
[3] Wang W Z, Deng N, Xin B J. Optik, 2020, 208: 164491. [本文引用:1]
[4] Gong L X, Zhu C X, Luo Y E, et al. Applied Spectroscopy, 2023, 77(2): 200. [本文引用:1]
[5] Kınlı F, Özcan B, Kiraç F. Journal of Visual Communication and Image Representation, 2025, 108: 104412. [本文引用:1]
[6] Celik T, Yetgin Z. Signal, Image and Video Processing, 2015, 9: 1889. [本文引用:1]
[7] Wang L X, Sole A, Hardeberg J Y, et al. Optics Express, 2021, 29(16): 24695. [本文引用:1]
[8] Ulucan O, Ulucan D, Ebner M. Investigating Color Illusions from the Perspective of Computional Color Constancy, 2023, arXiv: 2312. 13114. [本文引用:1]
[9] Sippel F, Seiler J, Genser N, et al. Journal of the Optical Society of America A-Optics, Image Science and Vision, 2020, 37(11): 1695. [本文引用:1]
[10] WANG Han, LI Chang-jun(王晗, 李长军). Laser and Optoelectronics Progress(激光与光电子学进展), 2022, 59(19): 1933001. [本文引用:1]
[11] Vršnak D, Domislović I, Subašić M, et al. IEEE Access, 2023, 11: 2128. [本文引用:1]
[12] Lazar M, Hladnik A. Sensors, 2023, 23(2): 1000. [本文引用:1]
[13] Robles-Kelly A, Wei R. A Convolutional Neural Network for Pixelwise Illuminant Recovery in Color and Spectral Images, International Conference on Pattern Recognition, 2018, 109. [本文引用:1]
[14] Xu B, Liu J, Hou X, et al. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020: 3616. [本文引用:1]
[15] Bianco S, Cusano C, Schettini R. IEEE Transactions on Image Processing, 2017, 26(9): 4347. [本文引用:1]
[16] Xie M D, Zhong C Z, He Y L, et al. 2025, arXiv: 2502. 12418. [本文引用:1]
[17] Afifi M, Hu Z H, Liang L. Optimizing Illuminant Estimation in Dual-Exposure HDR Imaging, in Computer Vision—ECCV 2024, Vol 15060, Springer, 2024. [本文引用:1]
[18] Li C X, Kang X J, Zhang Z F, et al. SWBNet: A Stable White Balance Network for sRGB Images, Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 1278. [本文引用:1]
[19] Xu J H, Luo M R, Fan H. Color Research and Application, 2023, 48(4): 368. [本文引用:1]
[20] Woo S, Park J, Lee J Y. CBAM: Convolution Block Attention Module, Proceedings of the European Conference on Computer Vision, 2018: 3. [本文引用:1]
[21] MA Xiang-cai, CAO Qian, BAI Chun-yan, et al(麻祥才, 曹前, 白春燕, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2024, 44(3): 610. [本文引用:1]
[22] Li Y Q, Fu Q, Heidrich W. Multispectral Illumination Estimation Using Deep Unrolling Network, IEEE Conference on Computer Vision, 2021, 12672. [本文引用:1]
[23] Bianco S, Cusano C, Schettini R. Color Constancy Using CNNs, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2015: 81. [本文引用:1]
[24] Hu Y M, Wang B Y, Lin S. FC4: Fully Convolutional Color Constance With Confidence-Weighted Pooling. IEEE Conference on Computer Vision and Pattern Recognition, 2017, 4085. [本文引用:1]
[25] Entok U C, Laakom F, Pakdaman F, et al. Pixel-Wise Color Constancy via Smoothness Techniques in Multi-Illuminant Scenes, IEEE International Conference on Image Processing, 2024: 2737. [本文引用:1]
[26] Du S S, Zhao D R, Guan L L, et al. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 4415514. [本文引用:1]
[27] Liang C, Zhao E L, Ma L. Proceedings of SPIE, 2024, 13227: 1322702. [本文引用:1]