引用本文
朱瑞, 笪耀东, 常勇强, 高杰, 石腾达, 张云刚. 基于自适应滑动窗吸收光谱的二氧化硫宽范围浓度测量[J]. 光谱学与光谱分析, 2025,45(8): 2134-2139.
ZHU Rui, DA Yao-dong, CHANG Yong-qiang, GAO Jie, SHI Teng-da, ZHANG Yun-gang. Wide Range Concentration Measurement of Sulfur Dioxide Based on Adaptive Sliding Window Absorption Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2025,45(8): 2134-2139.
Doi:10.3964/j.issn.1000-0593(2025)08-2134-06  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于自适应滑动窗吸收光谱的二氧化硫宽范围浓度测量
朱瑞1, 笪耀东2,3,5,*, 常勇强2,4,5, 高杰1, 石腾达2,3,5, 张云刚1,*
1.燕山大学电气工程学院, 河北 秦皇岛 066004
2.中国特种设备检测研究院, 北京 100029
3.国家市场监督管理总局技术创新中心(锅炉清洁低碳高效燃烧与安全评价), 北京 100029
4.国家市场监督管理总局重点实验室(特种设备安全与节能), 北京 100029
5.低碳热力发电技术与装备全国重点实验室, 北京 100029
*通讯作者 e-mail: dayaodong@csei.org.cn; zhangyg@ysu.edu.cn

作者简介: 朱 瑞, 2000年生, 燕山大学电气工程学院硕士研究生 e-mail: zhurui@stumail.ysu.edu.cn

收稿日期: 2024-12-03 修回日期: 2025-03-06
基金: 国家重点研发计划课题(2021YFF0600602)资助
摘要

二氧化硫(SO2)是化石燃料燃烧过程中不可避免的污染产物, 其浓度水平被认为是燃烧效率和能源利用率的关键指标, 因此实现燃烧过程中SO2的监测具有重意义。 吸收光谱技术凭借其准确度高、 稳定性强以及非接触式测量等特性, 在气体检测领域中展现出了广泛的应用前景。 然而, 在实际测量中, 高浓度SO2的吸收强度与浓度之间会出现严重的非线性, 这是SO2的宽范围浓度测量必须面对的问题。 为此, 对吸收光谱非线性的处理分析方法进行了实验研究, 提出了一种自适应滑动窗吸收光谱(ASWAS)技术。 实验中通过滑动窗自适应遍历和选择该特征吸收波段, 对其进行初次筛选和二次筛选, 最终反演获得最优测量结果。 与宽波段测量法和窄波段测量法相比, ASWAS在50~1 500 ppm浓度范围内的相对误差在1.3%以下, 表现出优异的性能。 实验分析结果表明, 该测量系统在低浓度和高浓度情况下的测量精度分别为0.80%和0.48%, 稳定性系数分别为0.28%和0.21%。 证明了提出的基于ASWAS的测量系统可以实现高精度、 高稳定性的SO2宽范围浓度测量, 为环境保护与能源利用领域内提供了一种有效的新思路和方法。

关键词: 二氧化硫; 自适应滑动窗吸收光谱; 浓度测量; 非线性
中图分类号:O433.1 文献标志码:A
Wide Range Concentration Measurement of Sulfur Dioxide Based on Adaptive Sliding Window Absorption Spectroscopy
ZHU Rui1, DA Yao-dong2,3,5,*, CHANG Yong-qiang2,4,5, GAO Jie1, SHI Teng-da2,3,5, ZHANG Yun-gang1,*
1. School of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China
2. China Special Equipment Inspection & Research Institute, Beijing 100029, China
3. Technology Innovation Center of Boiler Clean, Low-carbon, Efficient Combustion and Safety Evaluation, State Administration for Market Regulation, Beijing 100029, China
4. Key Laboratory of Special Equipment Safety and Energy-saving, State Administration for Market Regulation, Beijing 100029, China
5. State Key Laboratory of Low-carbon Thermal Power Generation Technology and Equipments, Beijing 100029, China
*Corresponding authors
Abstract

Sulfur dioxide (SO2) is an unavoidable pollutant product of the fossil fuel combustion process, and its concentration level is considered a key indicator of combustion efficiency and energy utilization, so it is of great significance to realize the monitoring of SO2 in the combustion process.Absorption spectroscopy technology has shown a wide range of applications in gas detection due to its high accuracy, strong stability, and non-contact measurement. However, a serious nonlinearity between the absorption intensity and the measured concentration of SO2 at high concentrations occurs in practical measurements, which interferes with the measurement of SO2 over a wide range of concentrations. To address this problem, an experimental study was conducted to analyze the treatment of nonlinearity in absorption spectra, and an adaptive sliding window absorption spectroscopy (ASWAS) technique was proposed. In the experiment, the sliding window adaptive traversal and selection of the characteristic absorption band, the first and second screening, and the final inversion were performed to obtain the optimal measurement results. Compared with the wide-band and narrow-band methods, ASWAS shows excellent performance with a relative error of less than 1.3% in the concentration range of 50 to 1 500 ppm.The experimental analysis results show that the measurement system has a measurement accuracy of 0.80% and 0.48% at low and high concentrations, and a stability coefficient of 0.28% and 0.21%, respectively. The above experimental results prove that the proposed measurement system based on ASWAS can realize the measurement of SO2 concentration in a wide range with high precision and high stability, which provides an effective new idea and method for environmental protection and energy utilization.

Keyword: Sulfur dioxide; Adaptive sliding window absorption spectroscopy; Concentration measurement; Nonlinearity
0.引言

在当前能源转换体系中, 化石燃料的燃烧虽然会对环境产生破坏, 但其仍占据主导地位[1, 2, 3]。 为提升燃烧效率并减轻环境污染, 优化燃烧过程显得尤为重要, 精确调控燃烧产物是其关键所在[4, 5, 6]。 二氧化硫(SO2)作为化石燃料燃烧的主要产物之一, 其浓度被视为评估及改进燃烧效率的关键指标[7, 8, 9]。 鉴于此, 在化石燃料燃烧过程中, 同步检测宽范围的SO2浓度对于促进燃烧效率的提升及降低环境的污染具有深远的意义。

目前, 有许多方法可以实现SO2的检测, 例如电化学传感、 光声光谱(photoacoustic spectroscopy, PAS)、 激光诱导荧光(laser-induced fluorescence, LIF)、 石英增强激光光谱(quartz-enhanced photoacoustic spectroscopy, QEPAS)、 吸收光谱[10, 11, 12, 13, 14, 15]。 其中, Lu等[16]开发了以不同摩尔比的Mn/Ce复合氧化物为传感电极材料的混合电位型二氧化硫传感器, 用于实现燃煤锅炉烟气中SO2的检测。 Zhao等[17]基于光纤耦合紫外发光二极管开发了全光学光声系统来检测SO2, 计算得到的检测限达到48 ppb。 此外, Weng等[18]利用宽带紫外吸收光谱和LIF技术定量检测燃烧环境中的SO2, 灵敏度达到2 ppm。 Zhang等[19]报道了一种基于可调谐二极管激光吸收光谱和支持向量回归结合的SO2传感器, 计算得到的检测限高达20 ppb。 不可否认, 上述所有研究都实现了SO2的精准测量。 然而上述的方法中, 电化学传感技术对环境温湿度较为敏感, 高温或者高湿环境可能会影响其零点、 灵敏度和使用寿命。 PAS技术可能由于气体浓度过高出现饱和现象, 导致光声信号不再随气体浓度的增加而增强。 同样的, LIF技术对于高浓度气体来说容易出现荧光猝灭现象, 导致无法准确测量气体浓度。 可调谐二极管激光吸收光谱技术在检测高浓度气体时, 由于气体分子的强吸收, 激光功率可能会发生衰减, 从而导致测量信号减弱。 QEPAS技术在高浓度SO2检测时仍面临信号饱和等问题, 限制了其测量范围。 本研究旨在克服上述方法的不是, 由于SO2在紫外波段有强吸收, 许多研究小组开发了基于紫外差分吸收光谱的SO2传感器。 Wang等[20]报道了一种基于紫外差分吸收光谱的高灵敏度SO2传感器, 波长范围为198~222 nm, 检测限为17 ppb。 Thalman等[21]对基于宽带腔增强吸收光谱技术的SO2检测方法进行了研究, 并实现了SO2的高精度动态测量。 在理想条件下, 根据朗伯-比尔定律, 吸收强度和浓度之间存在线性关系, 但实际测量中常出现线性偏差和非线性问题。 非线性会导致一系列问题, 包括测量结果曲线校准困难、 测量灵敏度和精度降低以及浓度测量范围有限。 上述研究中, 没有考虑在测量宽范围SO2浓度时出现的非线性问题。 因此, 有必要提出一种新的光学处理方法来消除这些因素引起的线性偏差。 滑动窗的概念在光谱学领域已被广泛用于选择光谱有效信息。 由于其在选择特征波长方面的出色性能, 本研究首次将滑动窗的思想引入光谱的非线性领域, 以解决宽范围SO2吸收强度和浓度之间出现的线性偏差。

在此提出了一种自适应滑动窗吸收光谱(adaptive sliding window absorption spectroscopy, ASWAS)方法, 用于实现宽范围SO2浓度的高精度检测。 它是一种数据处理方法, 在全光谱数据中生成具有自适应长度调节的滑动窗进行波段选择, 然后根据约束动态搜索最佳估计系数, 最终通过反演得到SO2的最佳浓度值。 通过评估计算结果的测量精度和稳定性, 有效地验证了该方法的可行性。 该方法为环境保护与能源利用领域内污染物气体的宽范围浓度检测提供了一种光学新方式。

1 ASWAS基本原理

ASWAS是一种基于吸收光谱的自适应数据处理方法, 主要是通过滑动窗对光谱数据特征进行精确结果近似的数据循环过程。 它可以消除传统光谱数据反演算法中的线性偏差问题, 实现气体浓度的精确测量。 不同测量波段反演得到的浓度值不同, 因此用于测量同一气体不同浓度的测量波段不是唯一固定的, 通过实现全光谱带的精确划分和最佳kbest筛选来确保不同浓度的准确测量。 滑动窗划分波段的过程可表示为

Si=S1+(i-1)ΔS0< i≤λe-z-S1ΔS+1Δλmin≤S1≤λe-z(1)

式(1)中, Δ S和Si分别为滑动窗的宽度增量和第i组滑动窗的宽度; λ e-z=λ e-λ z为分析波段, 其中λ z为起始波长, λ e为终止波长; Δ λ min为分析波段最小值。 在第i组滑动窗的宽度Si处, 按照滑动步长M划分整个吸收波段。 滑动窗的左右边界分别为λ l和λ r, 并且滑动窗的滑动规则可表示为

λl=λ0+nMλr=λ0+nM+Ni　(n=0, 1, 2, …)(2)

式(2)中, λ 0和n分别为滑动窗的起始左边界波长和滑动步数。 在这种情况下, λ 0等于λ z。 该研究中选择SO2的主要吸收波段进行研究, 起始波长和终止波长分别被设置为210和230 nm。 上述过程的原理示意图如图1所示。

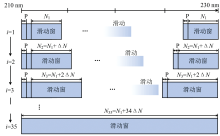图1 用于划分SO2特征吸收波段的滑动窗示意图Fig.1 Schematic diagram of the sliding window used to dynamically select the characteristic absorption wavebands of SO2

根据窗口宽度的设置规则和滑动窗的滑动规则来精确划分波段。 选择浓度为150 ppm的SO2标准吸收光谱作为参考光谱。 然后, 待测浓度的吸收光谱与参考光谱之间的关系可表示为

$F(k)=\sum_{\lambda}\left[P_{m}(\lambda)-k P_{s}(\lambda)\right]^{2}$ (3)

式(3)中, Pm(λ )为测量浓度的吸收光谱; Ps(λ )为参考光谱; k为F(k)最小值时的估计系数; F(k)为k的二次函数, 并且平方项的系数为正。 根据极值原则

∂F(k)∂k=0(4)

估计系数k的值可表示为

k=∑λPm(λ)Ps(λ)∑λPs2(λ)(5)

上述步骤中, 通过遍历不同组的不同波段得到k值的初步筛选结果。 相同窗口宽度的k值筛选规则可表示为

Ri=Uili·α|kin-kmax|≤ri(6)

式(6)中, Ri为第i组样本的选择距离; li为第i组样本的个数; Ui为第i组样本的标准差; α 为“ 3-sigma” 规则的标准化值; kin为第i组样本中第n个窗口的估计系数; kmax为当前组样本中相同窗口宽度的最大k值。 置信区间设为99.7, 区间内的所有k值都可以通过上述初次筛选过程得到, 即可以得到数据集E。 按照窗口宽度从窄到宽对数据集E中相应的k值依次编号后, 对其进行二次筛选。 二次筛选的目标函数可表示为

Q(kdj)=1Wd∑czce(kc-kdj)2　(j=1, 2, …, m)(7)

Wd=w-(d-1)Δwm=Ee-z-WdM'+1　(Wd≥2)(8)

cz=1+(j-1)M'ce=Wd+(j-1)M'　(cz≤c≤ce)(9)

式(7)中, Wd为当前窗口的宽度; w为起始窗口的宽度; M'为滑动步长; cz和ce分别为窗口的左边界和右边界; 数据集E中的k值被分为j组, 每组的窗口宽度相同; Ee-z为数据集E的维度, 即经过初次筛选后得到k值的个数; 数据集E根据窗口宽度以Δ w减小的过程遍历d次; kdj为二次筛选过程中第d个滑动窗在第j个窗口处的最佳k值。 随后, 式(7)中的kdj求导, 得到当前数据子集中的最优估计系数kdj, 该过程可表示为

∂Q(kdi)∂kdi=0(10)

式(10)中, 将求得的kdj代入式(7), 即可得到该子集的最优目标函数值Q(kdj)。 Q(kdj)反映了非线性影响下测量结果的离散程度, 其值越小, 说明系统的抗非线性能力越强, 稳定性越好。 在目标函数Q(kdj)小于1× 10-3时, 得到满足误差要求的kdj。 然后, 将得到的Q(kdj)由小到大排序, 并且将相应的kdj值代入式(7), 验证kdj值是否能使F(k)最小化。 如果当前的kdj满足要求, 则此时的kdj即为最优估计系数kbest。 否则, 顺序取下一个与Q(kdj)相对应的kdj进行验证, 直到F(k)达到最小值为止。 在本研究中, 上述参数设置为w=De-z、 M'=1和Δ w=1。 最佳浓度测量结果和其相对误差的计算过程可表示为

cm=kbest·c0(11)

e=|cm-ct|ct×100%(12)

式(11)和(12)中, ct和cm分别为待测气体的真实浓度和测量浓度; c0为参考光谱的标准浓度。 通过利用多组不同浓度的吸收光谱数据计算相对误差, 并且通过测量浓度来验证方法的可行性。

2 实验部分

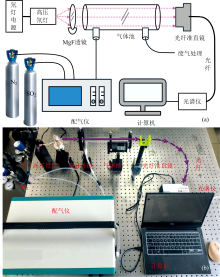
实验装置如图2(a, b)所示: 系统的光源为氘灯(A410JU, MILAS), 光源的平均寿命为2 000 h, 波长范围为160~400 nm。 透镜材质为氟化镁, 焦距为3 cm。 气体池的光程长度为25 cm, 材质为石英玻璃。 光谱仪(Maya 2000Pro, Ocean Insight)的分辨率为0.19 nm, 工作范围为172~320 nm。 本实验使用标准SO2浓度为2 000 ppm, 并且选择高纯氮气(N2)作为平衡气体。 配气仪(GC400, TUNKON)的测量精度和最大稀释比分别为± 0.5% F.S.和500∶ 1。 在本研究中, 通过配气仪将标准浓度SO2与高纯N2按不同比例混合制备不同浓度的SO2。 光源发出紫外线通过氟化镁透镜后射入气体池, 光纤接收到从气体池射出的出射光后传输给光谱仪。 计算机端海洋光学软件的参数中平均次数被设置为32次、 积分时间被设置为100 ms、 平滑度被设置为2。

图2 测量系统实验设计图
(a): 流程原理示意图; (b): 测量系统实物图Fig.2 Diagram of experimental design (a) and the photo of measurement system (b)

3 结果与讨论
3.1 SO2浓度筛选分析

采用的SO2特征吸收分析波段为210~230 nm, 对所有k值反演浓度进行了初次筛选和二次筛选, 并且以低浓度(100 ppm)、 中浓度(500 ppm)和高浓度(1 000 ppm)为例验证了该方法。 图3显示了不同波长宽度的滑动窗的浓度反演结果。 图3(a)中的黑色球体表示不同测量波段获得的浓度值, 初次筛选后获得的浓度值如图3(a)中的红色球体所示。 可以看出随着窗口的加宽, 反演浓度逐渐收敛于稳定值。 然后对从初次筛选(数据集E)获得的红色球体进行二次筛选, 得到SO2最佳浓度测量结果为99.3 ppm, 该值与稳定状态下达到的值非常接近。 基于这一分析, 可以得出结论, 宽波段更适合测量低浓度的SO2。 另一方面, 图3(b)中的测量值与上述结果不同, 初次筛选的数据没有收敛到稳定值。 对图3(b)中由红色球体组成的数据集E进行二次筛选后, SO2最佳浓度测量结果为503.1 ppm, 更接近中等窗口宽度获得的浓度值。 这可以表明, 随着浓度的增加, 适用的波段趋于变窄。 图3(c)中的原始测量数据在初始筛选后也没有收敛到稳定值, 第二次筛选计算出SO2最佳浓度测量结果为1 001.4 ppm, 这与窄测量波段反演得到的浓度值更相似。 由上述结果可以得出, 随着浓度的增加, 适用的波段变窄, 即使用窄的测量波段来计算高浓度SO2更准确。 上述三个SO2浓度的真实值和筛选后获得的测量结果证明了该方法筛选过程的可行性。 通过初次筛选和二次筛选, 最终计算出SO2的最佳浓度测量结果。

图3 不同浓度初次筛选和二次筛选的测量结果
(a): 100 ppm; (b): 500 ppm; (c): 1 000 ppmFig.3 Measured results of initial and secondary screening at different concentrations
(a): 100 ppm; (b): 500 ppm; (c): 1 000 ppm

3.2 系统测量结果

为了验证ASWAS的优异性能, 将其与窄波段测量法和宽波段测量法进行了比较, 测量结果如图4所示。 在210~230 nm范围内, SO2存在明显的特征吸收峰。 225~230 nm波段包含了一个较强的吸收峰, 适合作为窄波段代表; 而210~230 nm则涵盖了多个吸收峰, 能够反映宽波段特征。 因此, 分别以225~230和210~230 nm波段分别代表窄波段和宽波段。 从图中可以看出, 宽波段测量法在低浓度时表现出良好的线性, 但随着SO2浓度的增加, 测量结果的相对误差逐渐增加到58.8%, 在高浓度环境下难以准确测量SO2的浓度。 窄带测量法对于低浓度SO2测量结果的相对误差大部分超过了4%, 但是对高浓度SO2测量结果的相对误差都在3.6%以下。 上述结果表明这种方法窄带测量法更适合测量高浓度气体, 与宽带测量法相比, 在高浓度测量范围内显示出更好的测量能力。 然而, 由于225~230 nm仅代表一个窄带, 并非无限小, 随着SO2浓度的增加, 非线性仍会出现。 与上述两种测量方法相比, 本研究提出的ASWAS方法对于低浓度和高浓度SO2都有很好的测量能力, 在50~1 500 ppm的浓度范围内相对误差均小于1.3%。 上述讨论结果证明了ASWAS方法具有高精度SO2宽范围浓度测量的能力。

图4 不同方法的SO2测量结果和相对误差
(a): 窄波段测量法; (b): 宽波段测量法; (c): 自适应滑动窗吸收光谱Fig.4 SO2 measurement results and relative errors for different methods
(a): Narrow-band measurement; (b): Broad-band measurement; (c): ASWAS

3.3 测量精度和稳定性分析

为了验证该测量系统的测量精度和稳定性, 在低浓度(100 ppm)和高浓度(1 000 ppm)下分别采集了50组光谱数据。 ASWAS方法的测量结果如图5所示, 可以看出低浓度下测量结果波动范围为99.5~100.8 ppm, 误差范围为-0.5~0.8 ppm; 高浓度下测量结果波动范围为996.8~1 004.8 ppm, 误差范围为-3.2~4.8 ppm。 因此, 该测量系统在低浓度下的测量精度为0.80%, 在高浓度下的测量精度为0.48%, 表明该测量系统对SO2宽范围浓度测量具有出色的检测精度。 此外, 在低浓度SO2情况下, 测量结果的标准差和稳定性系数分别为0.28和0.28%; 在高浓度SO2情况下, 测量结果的标准差和稳定性系数分别为2.06和0.21%。

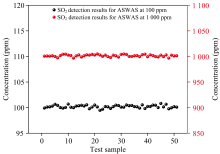图5 100和1 000 ppm浓度下ASWAS的SO2测量结果Fig.5 SO2 measured concentrations by ASWAS for 100 and 1 000 ppm concentrations

上述结果证明了该测量系统在测量SO2宽范围浓度方面具有良好的稳定性。

4 结论

提出了一种自适应滑动窗吸收光谱方法, 该方法成功抑制了高浓度下出现的非线性效应, 并且实现了宽范围SO2浓度的高精度测量。 首先, 通过滑动窗自适应遍历和划分SO2的特征吸收波段, 计算其估计系数。 然后, 根据初次筛选和二次筛选规则, 得到最优估计系数。 最后, 基于最优估计系数反演SO2浓度。 实验结果表明, 提出的ASWAS方法能够检测SO2的浓度范围为50~1 500 ppm。 在低浓度情况下的测量精度、 标准差和稳定性系数分别为0.80%、 0.28和0.28%; 在高浓度情况下测量精度、 标准差和稳定性系数分别为0.48%、 2.06和0.21%。 结果验证了ASWAS方法实现高精度宽范围SO2浓度测量的可行性, 为环境保护与能源利用领域内污染物气体的宽范围浓度检测提供了一种新的途径, 进一步推动了该领域检测技术的研究。

参考文献
[1] Dorokhov V V, Nagibin P S, Shlegel N E, et al. Fuel, 2024, 372: 132247. [本文引用:1]
[2] Yang B, Li W, Xie J, et al. Measurement, 2023, 214: 112766. [本文引用:1]
[3] GUO Xiu-rui, YAO Chang, LIU Yao, et al(郭秀锐, 姚畅, 刘瑶, 等). Journal of Beijing University of Technology(北京工业大学学报), 2024, 50(6): 733. [本文引用:1]
[4] Köse Ö, Koç Y, Yağlı H. Energy Conversion and Management, 2020, 211: 112745. [本文引用:1]
[5] Yao Z, Romero C, Baltrusaitis J. Fuel, 2023, 344: 128145. [本文引用:1]
[6] AO Wen(敖文). Chinese Journal of Explosives & Propellants(火炸药学报), 2023, 46(7): 10004. [本文引用:1]
[7] Vamvuka D, Zacheila K. Thermochimica Acta, 2024, 739: 179811. [本文引用:1]
[8] Obeid F, Van T C, Horchler E J, et al. Energy Conversion and Management: X, 2022, 14: 100179. [本文引用:1]
[9] Yi P, Wu Y, Meng C, et al. Journal of the Energy Institute, 2024, 114: 101590. [本文引用:1]
[10] ZHANG Xue-jun, CHEN Qin-gen, YANG Zhan, et al(张学军, 陈勤根, 杨展, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2024, 44(5): 1412. [本文引用:1]
[11] YANG Xi, XIA Hua, ZHANG Zhi-rong, et al(杨曦, 夏滑, 张志荣, 等). Chinese Journal of Lasers(中国激光), 2024, 51(17): 313. [本文引用:1]
[12] ZHANG Zhong-lin, YANG An-long, WANG Jiang, et al(张仲磷, 杨岸龙, 王江, 等). Chinese Optics(中国光学), 2024, 17(5): 1014. [本文引用:1]
[13] Wang R, Qiao S, He Y, et al. Opto-Electronic Advances, 2025, 8: 240275. [本文引用:1]
[14] Qiao S, He Y, Sun H, et al. Light: Science & Applications, 2024, 13(1): 100. [本文引用:1]
[15] Liu Y, Qiao S, Fang C, et al. Opto-Electronic Advances, 2024, 7(3): 230230. [本文引用:1]
[16] Lu Q, Zhang J, Wang B, et al. Sensors and Actuators B: Chemical, 2023, 377: 133050. [本文引用:1]
[17] Zhao X, Xu Y, Li C, et al. Sensors and Actuators B: Chemical, 2024, 403: 135193. [本文引用:1]
[18] Weng W, Aldén M, Li Z. Analytical Chemistry, 2019, 91(16): 10849. [本文引用:1]
[19] Zhang Y, Li Y, Yan J, et al. High Voltage, 2024, 9(4): 786. [本文引用:1]
[20] Wang L, Zhang Y, Zhou X, et al. Sensors and Actuators B: Chemical, 2017, 241: 146. [本文引用:1]
[21] Thalman R, Bhardwaj N, Flowerday C E, et al. Sensors, 2022, 22(7): 2626. [本文引用:1]