基于图像融合的多光谱辐射测温MC-CNN反演算法

引用本文

邢键, 朱自民, 崔双龙. 基于图像融合的多光谱辐射测温MC-CNN反演算法[J]. 光谱学与光谱分析, 2025,45(8): 2124-2127.
XING Jian, ZHU Zi-min, CUI Shuang-long. Multi Spectral Radiometric Temperature MC-CNN Inversion Algorithm Based on Image Fusion[J]. Spectroscopy and Spectral Analysis, 2025,45(8): 2124-2127.
Doi:10.3964/j.issn.1000-0593(2025)08-2124-04 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于图像融合的多光谱辐射测温MC-CNN反演算法

邢键, 朱自民, 崔双龙^*

东北林业大学计算机与控制工程学院, 黑龙江哈尔滨 150080

*通讯作者 e-mail: cui.shuanglong@qq.com

作者简介: 邢键, 1979年生, 东北林业大学计算机与控制工程学院教授 e-mail: xingniat@sina.com

收稿日期: 2024-11-19 修回日期: 2025-03-11

基金: 国家自然科学基金项目(62305053, 61975028)资助

摘要

多光谱辐射测温法是在一个仪器中设置多个光谱通道, 利用被测目标的多个光谱辐射亮度信息, 经数据处理得到被测目标的温度和目标材料的光谱发射率。该方法不需要辅助设备和附加信息, 对被测对象亦无特殊要求, 因而特别适用于高温目标的温度和材料发射率的同时测量。由于受未知的光谱发射率的影响, 多光谱辐射测温反演问题可归纳为在发射率约束条件下的欠定方程组求解问题, 传统的约束优化算法面对该问题存在求解时间长、惩罚系数调整困难导致算法不稳定等问题, 因此多光谱辐射测温反演算法一直是该领域研究的难点和热点。随着深度学习的不断发展, 为了充分利用深度学习算法在图像领域的精准特征识别能力解决多光谱辐射测温反演问题, 本文提出基于马尔可夫转换场(MTF)和格拉姆角场(GAF)多种光谱-温度图像融合的多通道卷积神经网络(MC-CNN)多光谱辐射测温反演算法。为了利用卷积神经网络在图像特征识别领域的明显优势, 提出利用MTF和GAF方法将一维的光谱-电压数据转换为具有光谱-温度特征的二维图像, 然后将携带光谱-温度特征的图像融合后输入改进的卷积神经网络网络进行训练, 从而实现温度反演。仿真结果表明, 8个光谱通道数据, 在温度2 355~2 624 K之间的1 K均分温度点进行反演的平均绝对误差为16.6 K, 平均相对误差为0.7%, 对火箭尾焰实测数据反演的误差与理论值相比均在±16.5 K内, 反演精度较高。该方法不受未知发射率的影响, 直接通过光谱-电压数据反演温度值, 进一步完善了多光谱辐射测温理论。

关键词: 多光谱测温; 图像转换; 神经网络; 反演

中图分类号:O140.3025 文献标志码:A

Multi Spectral Radiometric Temperature MC-CNN Inversion Algorithm Based on Image Fusion

XING Jian, ZHU Zi-min, CUI Shuang-long^*

College of Computer and Control Engineering, Northeast Forestry University, Harbin 150080, China

*Corresponding author

Abstract

Multispectral radiation thermometry is a method of creating multiple spectral channels in an instrument, using multiple spectral radiance information of the measured target, and processing the data to obtain the temperature. This method has no special requirements for the measured object, making it particularly suitable for simultaneous measurement of temperature and material emissivity of high-temperature targets. Due to the influence of unknown spectral emissivity, the problem of multispectral radiometric temperature inversion can be summarized as an underdetermined equation-solving problem under emissivity constraints. Therefore, multispectral radiometric temperature inversion algorithms have always been a difficult and hot research topic in this field. With the continuous development of deep learning, to fully utilize the precise feature recognition ability of deep learning algorithms in the image field to solve the problem of multispectral radiometric temperature inversion, this paper proposes a multi-channel convolutional neural network (MC-CNN) based on the fusion of Markov Transition Field (MTF) and Gramian Angular Field (GAF) for multispectral radiometric temperature inversion. Deep learning algorithms have obvious advantages in the field of image feature recognition. First, MTF and GAF methods convert one-dimensional spectral voltage data into two-dimensional images with spectral temperature features. Then, the images carrying spectral temperature features are input into an improved convolutional neural network for training, thereby achieving temperature inversion. The simulation results show that for 8 spectral channel data, the average absolute error of inversion at 1K evenly distributed temperature points between 2 355 and 2 624 K is 16.6 K, and the average relative error is 0.7%. Compared with the theoretical value, the inversion error of the measured data of the rocket tail flame is within ±16.5 K, indicating a high inversion accuracy. This method is not affected by unknown emissivity and directly uses spectral voltage data to invert temperature values, further improving the multispectral radiation temperature measurement theory.

Keyword: Multispectral temperature; Image conversion; Neural network; Inversion

文章图片

0. 引言

多光谱辐射测温技术利用多个光谱通道采集的辐射信息, 通过数据处理获得待测目标的温度值, 具有无测量上限、响应速度快及不干扰被测场等优点。目前, 多光谱辐射温度计的硬件结构基本成型, 但在理论方面, 受未知发射率的影响, 多光谱辐射测温理论仍待完善。目前, 多光谱辐射测温反演算法主要分为假设模型法^{[1, 2, 3]}、约束优化法^{[4, 5, 6, 7, 8, 9]}和神经网络法^{[10, 11, 12]}。假设模型法需要事先假设发射率模型, 如果假设模型与实际模型不符则反演结果误差较大; 约束优化算法则存在求解时间长、惩罚系数调整困难导致算法不稳定等问题; 神经网络法以BP神经网络法为主, 存在局部极小化的问题, 但是为利用神经网络反演温度的可行性提供了理论支撑。

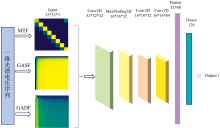
为了充分利用深度学习算法在图像领域的精准特征识别能力解决多光谱辐射测温反演问题, 本工作在参考温度模型的基础上, 提出了基于马尔可夫转换场(Markov transition field, MTF)和格拉姆角场(Gramian angular field, GAF)多通道卷积神经网络(multi-channel convolutional neural networks, MC-CNN)的多光谱辐射测温深度学习反演算法, 该方法不受未知发射率的影响, 仅利用多光谱辐射特征反演温度, 实现了深度学习与多光谱辐射测温技术的充分融合, 算法进一步完善了多光谱辐射测温理论。

1 参考温度模型

根据Plank公式, 对于多光谱高温计的第i个光谱通道, 输出的电压信号可以通过式(1)描述

$\frac{V_{i}}{V'_{i}} = ε (λ_{i}, T) \cdot e^{- C_{2} / λ_{i} T} \cdot e^{- C_{2} / λ_{i} T'}$ (1)

式(1)中, V_i为第i个光谱通道测量待测目标时所对应的电压; V'_i为标定时测量黑体目标时所对应的电压; ε (λ _i, T)是与光谱通道λ _i和待测温度T有关的光谱发射率; C₂为第二辐射常数; T'为标定时的黑体温度。如何在未知光谱发射率的情况下实现温度的反演, 是多光谱辐射测温理论的核心问题。

2 多光谱数据图像化

2.1 仿真数据集

为与实验验证数据一致, 将文献[13]中的8个光谱作为仿真光谱。 6类发射率样本包含“ ∨ 、 ∧ 、 w、 m型” 等10种发射率模型, 每种发射率模型又扩展为10组发射率。参考温度选为2 252 K, 待测温度为2 355~2 624 K之间的1 K均分270个温度点, 代入式(1), 得到仿真电压值, 共计27 000组数据进行仿真实验。

2.2 马尔可夫转换图像(MFT)法

首先, 将光谱-电压值归一化至[-1, 1], 如式(2)所示

$\tilde{x}_{i}=\frac{\left(x_{i}-\max X\right)+\left(x_{i}-\min X\right)}{\max X-\min X} $ (2)

依据序列的幅值特性, 将这些值离散化为Q个分位数单元。每个数值x_i都将映射到对应的分位数q_i上(q_i∈ [1, Q])。利用这些分位数, 构造一个基于马尔科夫转移概率的Q× Q矩阵w, 该矩阵反映了不同分位数之间的转移概率, 这一过程遵循一阶马尔科夫链原理, w的计算公式如式(3)所示

$w_{i j}=\sum_{\substack{\forall x \in q_{i}, y \in q_{j} \\ x+1=y}} \frac{1}{\sum_{j=1}^{Q} w_{i j}} $ (3)

将其拓展为马尔可夫转换场, 并通过MTF矩阵M来进行表示, 如式(4)所示

$M = [\begin{array}{l} m_{11} & m_{12} & \dots & m_{1 Q} \\ m_{21} & m_{22} & \dots & m_{2 Q} \\ ︙ & ︙ & ⋱ & ︙ \\ m_{Q 1} & m_{Q 2} & \dots & m_{QQ} \end{array}]$ (4)

式(4)中, m_ij为分位数q_i向分位数q_j转移概率。

2 355~2 362 K的温度相差1 K, 横纵坐标为光谱通道的MTF图像如图1所示。

	Figure Option View Download New Window
	图1 马尔可夫转换场(MTF)图片Fig.1 Markov transform field (MTF) image

2.3 格拉姆角场(GAF)法

同MTF转换法一样, 将光谱-电压值归一化至[-1, 1]; 将归一化后的序列数据映射到极坐标系统中, 每个数据对应的光谱通道看作半径r, 如式(5)所示

$\{\begin{array}{l} ϕ = \arccos {\tilde{x}}_{i}, & - 1 \leq {\tilde{x}}_{i} \leq 1, {\tilde{x}}_{i} \in \tilde{X} \\ r = n_{i} / N, & n_{i} \in N \end{array}$ (5)

通过反余弦函数计算得到的角度值均匀地分割成N个部分, 从而将点与光谱序列数据相对应起来。

根据格拉姆矩阵的定义, 如式(6)

$G = [\begin{array}{l} \cos (ϕ_{1, 1}) & \cos (ϕ_{1, 2}) & \dots & \cos (ϕ_{1, n}) \\ \cos (ϕ_{2, 1}) & \cos (ϕ_{2, 2}) & \dots & \cos (ϕ_{2, n}) \\ ︙ & ︙ & ⋱ & ︙ \\ \cos (φ_{n, 1}) & \cos (φ_{n, 1}) & \dots & \cos (φ_{n, n}) \end{array}]$ (6)

式(6)中, ϕ _i_,_j表示两个向量之间的夹角。可计算2种格拉姆角场, 即格拉姆和角场GASF式(7)与格拉姆差角场GADF式(8)

$GASF = [\begin{array}{l} \cos (ϕ_{1} + ϕ_{1}) & \dots & \cos (ϕ_{1} + ϕ_{n}) \\ \cos (ϕ_{2} + ϕ_{1}) & \dots & \cos (ϕ_{2} + ϕ_{n}) \\ ︙ & \cos (ϕ_{i} + ϕ_{i}) & ︙ \\ \cos (ϕ_{n} + ϕ_{1}) & \dots & \cos (ϕ_{n} + ϕ_{n}) \end{array}]$ (7)

$GADF = [\begin{array}{l} \cos (ϕ_{1} - ϕ_{1}) & \dots & \cos (ϕ_{1} - ϕ_{n}) \\ \cos (ϕ_{2} - ϕ_{1}) & \dots & \cos (ϕ_{2} - ϕ_{n}) \\ ︙ & \cos (ϕ_{i} - ϕ_{i}) & ︙ \\ \cos (ϕ_{n} - ϕ_{1}) & \dots & \cos (ϕ_{n} - ϕ_{n}) \end{array}]$ (8)

2 355~2 362 K的GASF和GADF温度相差1 K的图像如图2所示。

	Figure Option View Download New Window
	图2 GASF(a)和GADF图像(b)Fig.2 GASF (a) and GADF (b) images

3 MC-CNN温度反演网络

3.1 数据融合

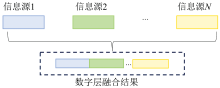
采用数据层融合, 将多源数据直接合并, 保持数据的初始状态和完整性, 避免信息损失。数据层融合可提供全方位数据特征信息, 有助于后续的特征提取, 数据融合如图3所示。

	Figure Option View Download New Window
	图3 数据层融合Fig.3 Data layer fusion

3.2 网络结构

网络结构如图4所示。该模型将MTF、 GASF和GADF图像同时输入网络。网络采用了堆叠3× 3小卷积核设计, 可更有效地捕捉图像的局部特征。同时, 在每组卷积层后整合了最大池化层, 大大减少了数据规模, 提升了反演效率, 为实时测温提供支撑。

	Figure Option View Download New Window
	图4 MC-CNN网络结构图Fig.4 MC-CNN network structure diagram

4 实验部分

4.1 仿真数据验证

为了验证MC-CNN算法, 相同数据下, 利用1D-CNN、 MTF-CNN、 MTF-VGGNet、 MC-CNN模型在待测温度为2 355~2 624 K之间的270个温度点反演, 结果如表1所示。

表1 算法结果对比 Table 1 Comparision of different algorithms

从表中可以看出, MC-CNN算法的平均绝对误差相较于主流算法MTF-VGGNet降低了30.5%, 最大误差降低了17.9%, 体现了MC-CNN算法的优势。

4.2 实测数据验证

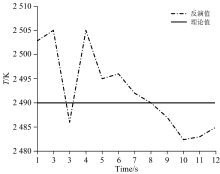
以文献[13]的火箭尾焰多光谱测温实际实验数据为基础, 将8波长高温计的12个测量时刻的电压数据转换为图像信息后送入经仿真数据训练好的MC-CNN网络, 结果如图5所示, 表明与理论值2 490.0 K的平均绝对误差为± 16.5 K, 精度较高, 满足实测精度要求。

	Figure Option View Download New Window
	图5 实测数据反演结果Fig.5 Inversion of measured data

5 结论

为了利用深度学习算法在图像识别领域的优势, 提出将光谱-电压数据通过马尔可夫转换和格拉姆角场法转换为多类二维图像, 同时输入改进的卷积神经网络算法MC-CNN实现了温度反演, 2 355~2 624 K温度区间仿真结果平均误差为± 16.6 K, 优于主流算法; 火箭尾焰2 490 K实测结果平均误差为± 16.5 K, 精度较高。该算法进一步完善了多光谱辐射测温理论。

参考文献

文献列表

[1]	Zheng S, Cai W G, Liu B, et al. Fuel. , 2023, 333: 126391. [本文引用:1]
[2]	SUN Bo-jun, SUN Xiao-gang, DAI Jing-min(孙博君, 孙晓刚, 戴景民). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(5): 1336. [本文引用:1]
[3]	Zheng S, Yang Y, Li X Y, et al. Fuel Processing Technology, 2020, 204: 106423. [本文引用:1]
[4]	Zou Z, Fu X, Zhang Y, et al. Infrared Physices & Technology, 2022, 127: 104385. [本文引用:1]
[5]	Chen L W, Zhang X Q, Gao S, et al. Optics Express, 2022, 30(20): 36603. [本文引用:1]
[6]	Zheng S, Cai W G, Sui R, et al. Fuel, 2022, 323: 124328. [本文引用:1]
[7]	Yang Z, Wang B, Dai J, et al. Results in Physics, 2023, 53: 107014. [本文引用:1]
[8]	Liang M, Wang Y, Wang C. Optics Express, 2023, 31(20): 33638. [本文引用:1]
[9]	Liang M, Wang Y, Wang C, et al. Measurement Science and Technology, 2022, 33(6): 65004. [本文引用:1]
[10]	Dong P K, Zhou L, Liu Z H, et al. Applied Optics, 2024, 63(30): 7900. [本文引用:1]
[11]	Zhang X, Han Y. Photonics. , 2024, 11(8): 767. [本文引用:1]
[12]	Jiang H, Tang R, Wang C Y, et al. IEEE Sensors Journal, 2024, 24(7): 10125. [本文引用:1]
[13]	Sun X G, Yuan G B, Dai J M, et al. International Journal of Thermophysics, 2005, 26(4): 1255. [本文引用:2]

2023

0.0