引用本文
谭小凤, 齐瑾, 李占峰, 张鹏. FY-3E太阳辐照度光谱仪可见光波段在轨光谱漂移特征分析与修正[J]. 光谱学与光谱分析, 2025,45(7): 2054-2060.
TAN Xiao-feng, QI Jin, LI Zhan-feng, ZHANG Peng. Analysis and Correction of On-Orbit Spectral Drift of FY-3E Solar Spectral Irradiance Monitor Visible Band[J]. Spectroscopy and Spectral Analysis, 2025,45(7): 2054-2060.
Doi:10.3964/j.issn.1000-0593(2025)07-2054-07  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
FY-3E太阳辐照度光谱仪可见光波段在轨光谱漂移特征分析与修正
谭小凤1,2, 齐瑾2,3,4,*, 李占峰5, 张鹏6,7,*
1.中国气象科学研究院, 北京 100081
2.国家卫星气象中心(国家空间天气监测预警中心), 北京 100081
3.许健民气象卫星创新中心, 北京 100081
4.中国气象局遥感卫星辐射测量和定标重点开放实验室, 北京 100081
5.中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033
6.中国气象局气象探测中心, 北京 100081
7.临近空间环境特性及效应全国重点实验室, 北京 100081
*通讯作者 e-mail: zhangp@cma.gov.cn; qijin@cma.gov.cn

作者简介: 谭小凤,女, 2000年生,中国气象科学研究院硕士研究生 e-mail: tanxiaofeng22@mails.ucas.ac.cn

收稿日期: 2024-09-30 修回日期: 2025-02-17 接受日期: 2025-02-17
基金: 国家重点研发计划项目(2022YFB3903105)资助
摘要

太阳辐照度光谱仪(SSIM)是我国首台自主研制的在大气层顶开展太阳连续光谱监测的跟踪式辐照度光谱仪, 它搭载于第二代极轨气象卫星风云三号黎明星(FY-3E)。 SSIM的光谱范围为165~2 400 nm, 在紫外和可见光波段具有1 nm的光谱分辨率, 以及0.1和0.25 nm间隔的采样率, 能够捕捉太阳精细光谱特征。 针对SSIM可见光波段获取的太阳光谱结构, 利用国际上最新发布的高分辨率太阳参考光谱TSIS-1 HSRS(Total and Spectral Solar Irradiance Sensor-1 Hybrid Solar Reference Spectrum, TSIS-1 HSRS)为定标基准, 分析2021年9月至2023年11月期间光谱的在轨变化特征, 评估在轨光谱定标精度。 基于太阳参考光谱的夫琅禾费吸收线特征, 利用仪器发射前测定的光谱狭缝函数卷积后得到与仪器特征相匹配的参考光谱, 筛选出9个夫琅禾费特征波长, 基于光谱匹配方法计算波长偏移, 分析在轨波长偏移随时间的变化特征, 并建立精细化订正方法提升仪器在轨光谱定标精度。 针对晨昏轨道对日观测的轨道运动特征, 首先分析了多普勒频移的年变化特征, 评估其在可见光波段可引起的波长最大偏移区间为-0.005~0.001 nm(700 nm 处)。 基于太阳夫琅禾费吸收线方法发现可见光波段光谱漂移的长期变化呈现周期性波动, 与在轨初期相比, 410 nm吸收线波长偏移的波动范围大致为-0.032~0.025 nm, 分析认为波长偏移与仪器温度的周期性波动有关, 各特征波长偏移与SSIM光栅温度的相关系数在-0.766~-0.964之间, 存在强的负相关。 针对波段内不同光谱位置的漂移特征, 利用光谱匹配方法分段滑动计算波长偏移, 再对其进行拟合修正, 修正结果显示光谱定标精度优于0.028 nm, 消除了卫星发射过程和在轨工作环境变化对光谱精度的影响, 以及仪器温度周期性波动导致的波长偏移, 长期稳定性较好, 有效提升了SSIM在轨光谱定标精度。 本文可为宽波段太阳光谱仪的在轨光谱定标研究提供参考。

关键词: 太阳光谱辐照度; 光谱定标; 太阳参考光谱; 可见光波段
中图分类号:TP722.4 文献标志码:A
Analysis and Correction of On-Orbit Spectral Drift of FY-3E Solar Spectral Irradiance Monitor Visible Band
TAN Xiao-feng1,2, QI Jin2,3,4,*, LI Zhan-feng5, ZHANG Peng6,7,*
1. Chinese Academy of Meteorological Sciences, Beijing 100081, China
2. National Satellite Meteorological Center (National Center for Space Weather), Beijing 100081, China
3. Innovation Center for FengYun Meteorological Satellite (FYSIC), Beijing 100081, China
4. Key Laboratory of Radiometric Calibration and Validation for Environmental Satellites, China Meteorological Administration, Beijing 100081, China
5. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China
6. Meteorological Observation Center, China Meteorological Administration, Beijing 100081, China
7. State Key Laboratory of Environment Characteristics and Effects for Near-Space, Beijing 100081, China
*Corresponding authors
Abstract

The Solar spectral irradiance monitor (SSIM) is China's first spaceborne solar irradiance spectrometer designed to measure solar continuum spectrumat the top of the atmosphere. It is mounted on the Fengyun-3E (FY-3E) satellite, the fifth satellite in the second generation of Chinese polar-orbit meteorological satellites. SSIM covers a spectral range from 165 to 2 400 nm, with a spectral resolution of 1 nm and sampling intervals of 0.1 and 0.25 nm in the ultraviolet and visible bands, which can capture fine solar spectrum characteristics of the sun. This study evaluated the spectral calibration accuracy of the SSIM visible band using the latest Total and Spectral Solar Irradiance Sensor-1 Hybrid Solar Reference Spectrum (TSIS-1 HSRS) as reference, with measurements from September 2021 to November 2023. By convoluting the pre-launch spectral slit function with TSIS-1 HSRS, a reference spectrum was generated to match the SSIM's characteristics. Using the spectrum matching method, nine solar Fraunhofer lines were selected to characterize wavelength shifts. The temporalvariationof spectral drift was analyzed, and a refined correction method was developed to improvethe spectral calibration accuracy of SSIM. Considering the characteristics of the early morning orbit, the annual variation of the Doppler shift was first analyzed, revealing the maximum wavelength shift of -0.005 to 0.001nm at 700 nm. Based on the assessment results of the Fraunhofer lines, the long-term variation of wavelength shifts in the visible band exhibited periodic fluctuations, with the shift of 410 nm varying from -0.032 to 0.025 nm compared to the initial on-orbit state. Further analysis indicates that the spectral driftis strongly correlated with the periodic fluctuations in the grating temperature of SSIM, with correlation coefficients between the wavelength shifts of the Fraunhofer lines and the grating temperature ranging from -0.766 to -0.964. Considering the drift characteristics on different spectral regions, the method of segmenting and sliding to calculate wavelength shifts and then fitting them for correction has been applied to the SSIM visible band, which shows that the results of spectral calibration accuracy are better than 0.028 nm. This method eliminates the impact of satellite launch, environmental changes on spectral accuracy, and also temperature fluctuations induced spectral drift. It has good long-term stability and effectively improves the on-orbit spectral calibration accuracy of SSIM. This paper provides a reference for the research on the on-orbit spectral calibration of wide-band solar spectrometers.

Keyword: Solar spectral irradiance; Spectral calibration; Solar reference spectrum; Visible band
引言

太阳是地球系统最主要的外部能量源, 其自身的能量波动具有周期性和波长依赖性, 而地球系统对其能量吸收的差异性驱动着地球气候和天气的变化[1, 2]。 太阳光谱辐照度(solar spectral irradiance, SSI)表征地球大气层顶入射太阳辐射不同波长的能量分布, 是气候模式、 痕量气体反演等多个研究领域的输入参数, 长期准确的太阳光谱辐照度数据是研究地气系统对太阳活动响应的重要基础[3, 4]。 太阳辐照度光谱仪(solar spectral irradiance monitor, SSIM)搭载于风云三号黎明星(FY-3E)上[5, 6], 于2021年7月5日成功发射, 是我国首次在晨昏轨道(局地过境时间为05:30)开展太阳辐射观测, 主要目标是通过紫外、 可见光和近红外三个波段获取大气层顶165~2 400 nm波长范围内高精度逐日太阳连续光谱。 SSIM是扫描型光栅光谱仪, 完成整条太阳光谱观测需要约20 min, 它的主要性能指标如表1所示。

表1 SSIM仪器主要性能指标 Table 1 SSIM instrument properties

仪器发射前在地面实验室已对其光谱和辐射特征进行精细标定。 由于仪器在发射过程中的冲击振动、 在轨运行期间的环境变化以及自身老化等因素, 仪器已测定的精度可能会发生变化, 因此在轨定标对于保持仪器的精度和稳定度至关重要。 光谱定标是辐射定标的前提, 在轨光谱定标方法主要分为两大类: 一是仪器设计有星上光谱定标装置, 利用精确已知的特征谱线位置作为参考基准, 通过实测结果与已知标准谱线比较确保光谱测量的准确性; 二是利用外部参考基准, 以仪器观测目标物自身的特征谱线为参考, 比如太阳夫琅禾费吸收线、 大气吸收带等[7, 8, 9, 10, 11]。

本文基于SSIM可见光谱仪在轨测量结果的实际响应特征, 利用太阳夫琅禾费吸收线特征提出针对性在轨光谱定标方法, 分析仪器在轨以来的波长变化特征, 并开展波段的光谱漂移订正。 将高分辨率的太阳参考光谱作为定标基准, 基于光谱匹配方法首先在卷积后的仪器参考光谱中筛选出9个吸收特征明显的吸收线, 通过相关系数计算得到波长在轨偏移, 分析波长偏移与SSIM可见光谱仪光栅温度的相关性, 最后优化算法对整个波段的光谱漂移进行订正, 给出了订正后的评估结果, 表明该方法可以消除光谱温漂的现象, 有效提升了SSIM的在轨光谱定标精度。

1 原理和方法
1.1 SSIM可见光波段发射前光谱定标方法

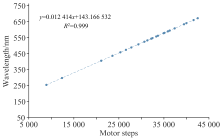
单一特征谱线经过仪器光栅会被展宽至仪器的光谱分辨率, 形成具有仪器特性的光谱响应谱线。 在已知特征谱线位置的情况下, 通过高斯拟合可得到中心位置(即特征谱线波长)对应的仪器电机步数和光谱分辨率。 SSIM在发射前以汞灯特征波长(9组)和一系列稳频激光光源(共16组)为光谱定标基准, 分别进行高斯拟合得到波长与电机步数数据, 建立波长定标方程:

λ=aj+b(1)

式(1)中, j为丝杠电机步数, λ 为波长, a、 b为定标系数。 通过最小二乘拟合得到的波长公式如图1所示, 在线性拟合下R2优于0.999。

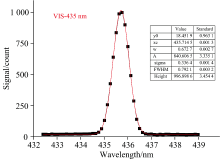
图1 VIS波段波长定标公式Fig.1 Wavelength calibration formula for the VIS band

在卫星发射前, SSIM仪器利用卤钨灯和汞灯对仪器的光谱特征参数进行核查, 包含光谱范围、 光谱采样间隔、 光谱分辨率、 波长重复性和波长定标精度5项光谱性能指标测试结果如表2所示。 图2给出了在汞灯特征谱线435 nm处的高斯拟合结果。

表2 SSIM可见光波段发射前光谱定标结果 Table 2 Pre-launch spectral calibration results of SSIM VIS band

图2 汞灯435 nm光谱响应曲线高斯拟合Fig.2 Gaussian fitting of spectral response curve of mercury lamp at 435 nm

1.2 SSIM可见光波段在轨光谱定标方法

太阳夫琅禾费吸收线广泛分布于太阳光谱中, 这些吸收线由太阳大气层的元素吸收导致, 是独立于仪器之外的目标物特征。 本文基于太阳夫琅禾费吸收线特征, 针对SSIM可见光波段1 nm光谱分辨率、 0.05 nm光谱定标精度需求开展在轨光谱定标研究, 以TSIS-1 HSRS高分辨率太阳参考光谱[12]作为参考基准, 将TSIS-1 HSRS与SSIM的光谱响应函数卷积, 再利用卷积后的参考光谱与SSIM光谱进行光谱匹配, 以此计算SSIM在轨波长偏移, 并开展精细订正。

1.2.1 太阳参考光谱的处理

太阳参考光谱Sref(λ )需要与SSIM的光谱响应函数F(λ )进行卷积运算获得仪器光谱分辨率下的理论参考光谱S(λ ), 由式(2)计算

S(λ)=∫Sref(λ)F(λ)dλ∫F(λ)dλ(2)

当SSIM波长偏移β 时, 相应的光谱响应函数会随之变化

F(λj, β)=12πσje-[λ-(λj-β)]22σj2(3)

1.2.2 构建光谱匹配的评价函数及确定最优波长偏移

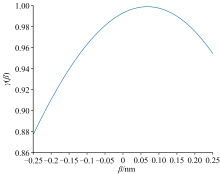
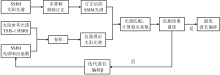
利用皮尔森相关系数确定SSIM观测光谱与参考光谱的最佳匹配, 如式(4), 其中M(λ j)和S(λ j, β )分别为SSIM观测光谱和参考光谱, N为光谱采样点个数。 迭代波长偏移β 计算相关系数, 求得相关系数最大值对应的β 作为评估结果。 相关系数γ (β )随波长偏移β 的变化关系如图3所示, 在一定范围内, 存在SSIM光谱与参考光谱的最大相关性。 利用Nelder-Mead单纯形数值优化方法寻找波长偏移的最优解, 当β 趋近于SSIM波长实际偏移量时, 相关系数γ (β )逐渐收敛, 趋向于达到最大值, 认为此时SSIM光谱与参考光谱的差异最小, 从而实现光谱曲线的最佳匹配。 光谱匹配算法流程如图4所示。

$\gamma(\beta)=\frac{\sum_{j=1}^{N}\left(M\left(\lambda_{j}\right)-\overline{M\left(\lambda_{j}\right)}\right)\left(S\left(\lambda_{j}, \beta\right)-\overline{S\left(\lambda_{j}, \beta\right)}\right)}{\sqrt{\sum_{j=1}^{N}\left(M\left(\lambda_{j}\right)-\overline{M\left(\lambda_{j}\right)}\right)^{2}} \sqrt{\sum_{j=1}^{N}\left(S\left(\lambda_{j}, \beta\right)-\overline{S\left(\lambda_{j}, \beta\right)}\right)^{2}}}$(4)

图3 相关系数γ (β )与β 的关系Fig.3 The relationship between γ (β ) and β

图4 光谱匹配算法流程Fig.4 Flow chart of the spectrum-matching algorithm

1.2.3 可见光波段光谱漂移订正

为了精确修正SSIM在可见光波段的光谱漂移, 采用了细分谱段滑动窗口方法进行波段处理, 设置窗口长度为25 nm, 步长为2.5 nm, 将SSIM可见光波段划分为若干小谱段。 逐谱段应用光谱匹配方法计算波长偏移, 再对全部小谱段的波长偏移进行多项式拟合, 得到SSIM探测点的订正量, 从而实现SSIM高精度的波长偏移订正。 该方法能够很好的覆盖全波段, 但在1 nm光谱分辨率下, 有些小谱段经卷积后无强吸收线特征, 对方法的应用有一定影响。

2 在轨光谱定标特征

尽管SSIM在发射前经过了实验室定标, 但是实际在轨工作状态下需要进行卫星运行轨道速度引起的多普勒频移订正, 同时由于实际在轨的工作环境有别于实验室环境, 并且随着卫星-太阳的位置, SSIM在轨工作的温度、 辐射环境时刻在发生变化, 所以需要通过长期的数据了解SSIM在轨的光谱定标随着时间的变化特征。

2.1 晨昏轨道多普勒频移订正

SSIM对日观测光谱需修正因相对运动产生的多普勒效应。 在光谱维上, 波长偏移与多普勒效应因子fdoppler呈线性关系, 可利用式(5)和式(6)进行订正

fdoppler=1-vrelc(5)

λ0=λinstrument×fdoppler(6)

式(5)和式(6)中, vrel为卫星与太阳的相对速度(二者相互靠近时, vrel为负值), c为光速, λ instrument为仪器观测波长位置。

图5显示了2023年SSIM对日观测状态下在280和700 nm两个波段极值波长由多普勒频移引起的波长偏移, 2023年700 nm波长处的偏移在-0.005~0.001 nm之间, 280 nm的波长偏移为-0.002~0.000 5 nm。 对于SSIM可见光波段整体而言, 多普勒频移引起的波长偏移相对较小, 不到波长定标精度的1/5。

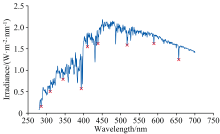
图5 280和700 nm波长处的多普勒频移Fig.5 Doppler shifts at 280 and 700 nm

2.2 SSIM在轨光谱定标特征分析

鉴于SSIM可见光波段的光谱覆盖范围较广, 选定了9条具有代表性的太阳夫琅禾费吸收线, 截取吸收线附近10 nm的光谱区域利用光谱匹配方法逐段计算波长偏移, 分析SSIM光谱不同位置波长偏移特征。 图6为选定的9条夫琅禾费吸收线, 它们均匀分布在SSIM可见光波段内。

图6 所选太阳夫琅禾费吸收线Fig.6 Selected the Fraunhofer lines

图7(a)显示了2021年9月— 2023年11月期间所选9条夫琅禾费吸收线的波长偏移时序特征, 波长偏移为正值时, 代表SSIM光谱相对于参考光谱向长波方向漂移。 长期监测结果显示出不同吸收线的波长偏移具有相似的时间变化趋势, 存在周期性波动, 部分波长偏移已超出了波长定标精度指标(≤ 0.05 nm)。 图7(b)显示了不同时期波长偏移的光谱分布特征, 可以看到吸收线的波长偏移在SSIM可见光波段内呈现出特定的分布结构, 340~700 nm波段范围内的波长偏移均向长波方向漂移, 而在280~340 nm之间的两个吸收线位置的偏移方向与之相反。 这种结构说明了仪器在轨环境与地面实验室定标环境有差异, 波长定标公式的斜率发生变化, 新旧斜率交叉点的一侧偏小, 另一侧偏大。

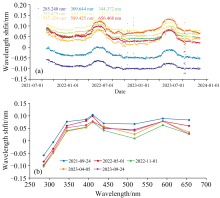图7 (a) 太阳夫琅禾费吸收线波长偏移的时间变化; (b) 太阳夫琅禾费吸收线波长偏移的分布Fig.7 (a) Temporal variation of wavelength shifts of the Fraunhofer lines; (b) The distribution of wavelength shifts of the Fraunhofer lines

在轨仪器温度变化通常是影响其性能的重要因素, 图8显示了SSIM光栅温度的变化趋势, 与图7(a)比对分析发现, 相对于在轨初始状态, 光栅温度升高, SSIM光谱向短波方向漂移, 光栅温度降低, SSIM光谱向长波方向漂移, 进一步说明了光栅温度变化引发的形变对仪器光谱性能的影响。

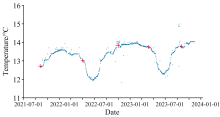图8 SSIM光栅温度
红色标记符号为图7(b)所选日期的温度Fig.8 The grating temperature of SSIM
The red marker symbols are the temperatures for the dates selected in Figure 7(b)

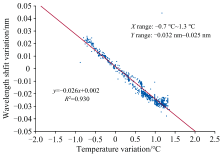
分别计算9条吸收线的波长偏移与光栅温度的相关系数如表3 所示, 计算结果处于-0.766~-0.964之间, 表明二者之间存在强相关性。 图9展示了负相关系数最高的410 nm吸收线波长偏移和光栅温度相对于在轨初期(2021年9月24日)的变化量之间的散点图。 由图可见, 仪器可见光光栅的在轨温度变化约为-0.7~1.3 ℃, 波长位置变化约为-0.032~0.025 nm。

表3 太阳夫琅禾费吸收线波长偏移与SSIM光栅温度的相关系数 Table 3 The correlation coefficients between wavelength shifts of the Fraunhofer lines and SSIM grating temperature

图9 相对于2021年9月24日的波长偏移相对变化与温度相对变化之间的关系Fig.9 The relationship between wavelength shifts relative change and temperature relative change to September 24, 2021

3 SSIM在轨光谱漂移修正

利用1.2.3中介绍的细分谱段滑动窗口方法, 将分段计算的波长偏移再拟合, 用于修正SSIM可见光波段太阳光谱。 图10(a)为细分谱段评估波长偏移的计算结果, 显示在SSIM可见光波段中段的波长偏移较为一致, 具有较好的连续性; 550~650 nm间的结果波动与该段太阳光谱较平滑无强夫琅禾费吸收线有关。 通过多项式拟合对光谱漂移进行修正, 随后将修正后的SSIM光谱与参考光谱重新匹配计算波长偏移, 修正效果如图10(b)所示, 可以看到可见光波段两端的不稳定性得到了显著改善, 整个工作波段内的波长偏移均在0.05 nm以内。

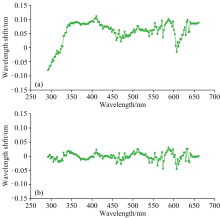图10 (a) SSIM可见光波段光谱漂移未修正评估结果; (b) SSIM可见光波段光谱漂移修正后评估结果Fig.10 (a) The uncorrected spectral drift in the VIS band of SSIM; (b) The spectral drift after correction in the VIS band of SSIM

图11给出了波长偏移修正前后特征谱线的效果图, 由图可见在仪器1 nm的光谱分辨率下, 在轨的波长偏移是相对小量, 本方法能够改善观测与参考光谱的一致性。 图12显示了修正后特征波长偏移的长期变化, 相较于图7的监测结果图, 有效修正了原有的光谱漂移以及周期性温度波动对其的影响, 稳定性较好, 光谱定标精度小于0.028 nm。 对2021年9月至2023年11月在轨运行期间光谱漂移修正前后太阳夫琅禾费吸收线的波长偏移进行统计分析, 如表4所示, 其中未修正的吸收线波长偏移的标准差介于0.012至0.023 nm之间, 波动程度较为一致, 但均值不同, 经过修正, 吸收线的波长偏移降至0.028 nm以下, 标准差小于0.012 nm, 多个吸收线波长偏移的标准差小于0.005 nm, 显示出修正后的波长具有较好的精度和稳定性。 总体而言, 采用分段滑动评估并修正波长偏移的方法可以满足SSIM可见光波段的波长定标需求, 显著提升了SSIM光谱数据的整体质量和可靠性。

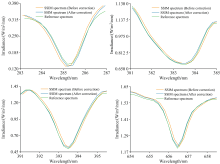图11 修正前后SSIM光谱和太阳参考光谱的夫琅禾费吸收线Fig.11 The Fraunhofer lines in the SSIM spectrum before and after correction, and in the solar reference spectrum

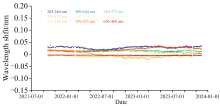图12 光谱漂移修正后太阳夫琅禾费吸收线波长偏移的时间变化Fig.12 Temporal variation of wavelength shifts of the Fraunhofer lines after correction

表4 光谱漂移修正前后太阳夫琅禾费吸收线波长偏移的统计结果 Table 4 Statistics ofwavelength shifts of the Fraunhofer lines before and after correction
4 结论

为了满足SSIM入轨后对光谱定标精度的高指标要求, 本文利用太阳夫琅禾费吸收线的特征结构建立在轨波长参考基准, 基于光谱匹配方法开展在轨光谱定标, 以相关系数得到最优波长偏移评估结果, 分析了波长偏移的周期性波动原因, 在此基础上针对可见光波段的280~700 nm波段范围提出以25 nm小谱段最优匹配以2.5 nm步长滑动的方法实现对整个谱段光谱漂移的精细评估, 再利用多项式拟合实现对波段的最优修正, 并针对修正效果给出统计分析与评价。

基于筛选的9个太阳夫琅禾费吸收线长时序的波长偏移特征, 揭示了仪器在轨后相较地面实验室的环境差异影响和受工作环境长期影响的变化特征, 统计分析表明, 它们的偏移均值在-0.089~0.09 nm之间, 偏移标准差为0.012~0.023 nm, 波动幅度较为一致。 这种周期性波动与SSIM光栅温度的周期性变化呈现强相关性, 通过定量分析, 建立二者的变化响应关系, 其线性拟合的R2为0.930。 通过细分谱段计算波长偏移, 再运用多项式拟合修正的结果显示, 修正后SSIM的光谱定标精度优于0.028 nm, 偏移标准差较修正前普遍减少50%~80%。

本文针对SSIM可见光波段光谱在轨变化特征, 提出以光谱匹配方法开展定量分析与光谱漂移修正算法, 基于该方法可实现在SSIM可见光波段1 nm的光谱分辨率下, 在轨长时序光谱定标精度优于0.028 nm。 在此过程中, 分析了仪器波长漂移与光栅温度变化的响应关系, 建立的定量线性模型显示, 要实现与算法相当的光谱精度, 仪器在轨温度波动需小于1.1 ℃, 可作为仪器指标优化的数据支撑。 本文可为宽波段太阳光谱仪的在轨光谱定标研究提供参考。

参考文献
[1] XIAO Zi-niu(肖子牛). Chinese Journal of Nature(自然杂志), 2021, 43(6): 408. [本文引用:1]
[2] DING Yi-hui(丁一汇). Meteorological Monthly(气象), 2019, 45(3): 297. [本文引用:1]
[3] Ermolli I, Matthes K, de Wit T D, et al. Atmospheric Chemistryand Physics, 2013, 13(8): 3945. [本文引用:1]
[4] Thuillier G, Zhu P, Snow M, et al. Light-Science & Applications, 2022, 11(1): 79. [本文引用:1]
[5] Zhang P, Hu X Q, Sun L, et al. Bulletin of the American Meteorological Society, 2024, 105(1): E144. [本文引用:1]
[6] Zhang P, Hu X Q, Lu Q F, et al. Advances in Atmospheric Sciences, 2022, 39(1): 1. [本文引用:1]
[7] LI Zhan-feng, WANG Shu-rong, HUANG Yu, et al(李占峰, 王淑荣, 黄煜, 等). Acta Optica Sinica(光学学报), 2013, 33(2): 0228002. [本文引用:1]
[8] Kang M, Ahn M H, Liu X, et al. Remote Sensing, 2020, 12(17): 2846. [本文引用:1]
[9] WANG Hong-bo, HUANG Xiao-xian, FANG Chen-yan, et al(王宏博, 黄小仙, 房陈岩, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2018, 38(1): 296. [本文引用:1]
[10] BI Yan-meng, WANG Qian, YANG Zhong-dong, et al(毕研盟, 王倩, 杨忠东, 等). Chinese Journal of Atmospheric Sciences(大气科学), 2022, 46(3): 645. [本文引用:1]
[11] ZHANG Ya-qiong, ZHANG Wen-juan, CHEN Zheng-chao, et al(张雅琼, 张文娟, 陈正超, 等). Journal of Infrared and Millimeter Waves(红外与毫米波学报), 2015, 34(3): 360. [本文引用:1]
[12] Coddington O M, Richard E C, Harber D, et al. Geophysical Research Letters, 2021, 48(12): e2020GL091709. [本文引用:1]