基于色彩感知的通用高保真光谱图像压缩

引用本文

梁玮, 蔡磊, 郝雯, 金海燕, 侯煜. 基于色彩感知的通用高保真光谱图像压缩[J]. 光谱学与光谱分析, 2025,45(7): 2008-2016.
LIANG Wei, CAI Lei, HAO Wen, JIN Hai-yan, HOU Yu. Universal High Fidelity Spectral Image Compression Based on Color Perception[J]. Spectroscopy and Spectral Analysis, 2025,45(7): 2008-2016.
Doi:10.3964/j.issn.1000-0593(2025)07-2008-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于色彩感知的通用高保真光谱图像压缩

梁玮^1,², 蔡磊^1,², 郝雯^1,², 金海燕^1,², 侯煜³

1.西安理工大学计算机科学与工程学院, 陕西西安 710048

2.陕西省网络计算与安全技术重点实验室, 陕西西安 710048

3.中国人民解放军陆军工程大学基础部, 江苏南京 211101

作者简介: 梁玮,女, 1985年生,西安理工大学计算机科学与工程学院讲师 e-mail: wliang@xaut.edu.cn

收稿日期: 2024-06-28 修回日期: 2025-02-01 接受日期: 2025-02-01

基金: 陕西省自然科学基础研究计划项目(2024JC-YBMS-477, 2023-JC-YB-545),国家自然科学基金面上项目(62372369)资助

摘要

针对光谱图像在特定再现环境下的色彩高保真复制等领域的应用, 为增加通用性, 提升压缩效率, 进一步存储传输, 本文提出了特定光照中基于视觉感知特性的通用低复杂度色彩高保真光谱图像压缩方法。首先研究特定再现环境中光谱图像的色彩再现原理, 设计重建光谱图像色彩误差衡量方式, 进而提出特定光照中光谱图像色彩保真压缩的失真指导准则。基于色彩失真指导准则, 得出压缩原理, 进而设计光谱预处理、空谱去冗余方法、编码方法和优化策略, 最终提出可供高保真再现的光谱图像压缩方法。在失真指导准则方面, 首先构建了光谱图像的色彩分解环境, 提出了对光谱图像在特定照明下(单一或者混合照明)进行色彩感知信息提取的矩阵算子; 然后, 利用色彩感知信息提取算子, 采用色彩感知误差衡量光谱图像于色彩测度上的偏差; 最后, 提出用于指导压缩环节的光谱图像色彩感知失真准则。基于该准则提出针对性压缩原理, 设计了本文压缩算法流程。首先, 对光谱数据色彩感知加权预处理, 采用色彩感知信息提取算子, 获得特定再现条件下保持光谱特性的光谱色彩感知数据; 然后, 基于色彩感知压缩原理, 对色彩感知光谱数据进行APWS-RA编码, 命名为W_SF-APWS-RA。光谱图像解码分为两个阶段。首先, 对压缩码流进行编码的逆处理, 形成重建的光谱色彩感知数据矩阵; 然后, 采用设计的可逆色彩感知提取算子, 通过感知信息提取矩阵算子的逆矩阵与重建光谱色彩感知数据矩阵相乘获得重构光谱图像。实验表明, 在相同比特率下, 较低复杂度压缩APWS, APWS-RA及色彩再现类WF-APWS-RA, W_SF-APWS-RA编码不但能够更加有效地保留特定再现条件下的光谱色彩信息, 具有最优秀的变光照色彩再现稳定性, 同时可有效提升光谱重建精度。因此, 新方法亦可泛化用于遥感等领域, 具有重要实用价值。

关键词: 可见光谱; 光谱图像压缩; 色彩高保真再现; 色彩感知信息提取; 小波编解码

中图分类号:TN919.81 文献标志码:A

Universal High Fidelity Spectral Image Compression Based on Color Perception

LIANG Wei^1,², CAI Lei^1,², HAO Wen^1,², JIN Hai-yan^1,², HOU Yu³

1. School of Computer Science and Engineering, Xi'an University of Technology, Xi'an 710048, China

2. Shaanxi Key Laboratory for Network Computing and Security Technology, Xi'an 710048, China

3. Basic Department, Army Engineering University of Chinese People's Liberation Army, Nanjing 211101, China

Abstract

Aiming at the application of spectral images in the fields of color high fidelity reproduction in specific reproduction environments, this paper proposes universal low-complexity, color-high-fidelity spectral image compression methods based on visual characteristics in specific illumination, which could enhance algorithms' versatility, improve compression efficiency, and further facilitate images' storage and transmission. This paper first studies the color reproduction principle of spectral images in specific reproduction environments, designs a measurement method for the color error of reconstructed spectral images, and then proposes distortion guidelines for spectral image color fidelity compression in specific illumination. Based on the color distortion guidelines, the compression principle is derived. Then spectral preprocessing, spatial-spectral de-redundancy methods, encoding methods, and optimization strategies are designed, and finally, spectral image compression methods for high-fidelity reproduction are proposed. In terms of distortion guidance criteria, first the color decomposition environment of spectral images is constructed, and a matrix operator is proposed to extract color perception information from spectral images under specific lighting (single or mixed lighting); then, through the color perception information extraction operator, color perception error is used to measure the deviation of spectral images in the color measurement; finally, the color perception distortion criterion of the spectral image is proposed to guide the compression process. Based on this criterion, a targeted compression principle is proposed, and the compression flow of this paper is designed. First, the color perception weighted preprocessing of the spectral data is performed, and the color perception information extraction operator is used to obtain spectral color perception data under specific reproduction conditions that still maintains spectral characteristics; then, based on the color perception compression principle, APWS-RA encoding is performed on the color perception spectral data. The method is named W_SF-APWS-RA. Spectral image decoding is divided into two stages. First, the compressed bit stream is encoded inversely to form a reconstructed spectral color perception data matrix; then, the reconstructed spectral image is obtained by multiplying the inverse matrix of the perception information extraction operator and the reconstructed spectral color perception data matrix. Experiments show that at the same bit rate, compared with the existing low-complexity APWS, APWS-RA, and universal color-high-fidelity WF-APWS-RA compression, WsF-APWS-RA codings can not only more effectively retain spectral color information under specific reproduction conditions, but also have the best variable illumination color reproduction stability. Meanwhile, it can also effectively improve the accuracy of spectral reconstruction. Therefore, the new methods can also be generalized to remote sensing and other fields, and have important practical value.

Keyword: Visible spectrum; Spectral image compression; High-fidelity color reproduction; Color perception information extraction; Wavelet codec

文章图片

引言

多光谱图像(在色彩复制领域, 光谱图像谱间通常31维或以上, 统称为多光谱图像)被视为物体光学“ 指纹” 。其采用光谱反射率数值描述场景信息, 是一种结合了二维空间信息和一维光谱信息的三维数据立方体。与传统RGB图像的色度三通道记色模式不同, 光谱图像记录物体固有属性, 可结合任意外部环境呈现精准、一致的颜色, 具备色度图像无法企及的超强色彩再现能力, 因此对高保真颜色科学与颜色复制技术的推进举足轻重, 在光谱打印、文化遗产修复、电子医疗、纺织印染、汽车喷漆、食品安全等领域有着重要的实用价值。然而, 多光谱图像数据量庞大、维度高, 存储、传输、再现困难。为高效存储和传输, 并且保证其后续再现等应用需求, 必须充分利用其光谱特性, 进行合理的按需有效压缩。

目前, 光谱图像压缩集中应用于航空航天遥感, 通常包含三个处理阶段: 压缩指导准则、去相关性以及编码^[1]。算法在压缩准则的指导下按需去除相关性并进行优化编码, 压缩指导准则体现为光谱均方误差, 去相关性表现为去除准则意义下的空谱冗余, 编码则充分利用去冗余后的数据特征, 形成应用需求下的二进制码流。随着深度学习在计算机视觉任务中的兴起, AEs、 VAEs、 CNNs、 RNNs、 GANs等网络架构先后应用于静态色度图像压缩^{[2, 3, 4]}。然而, 学习式压缩采用深度网络进行准则指导下的特征提取, 训练时间长, 且其生成图通常并不具备较好的熵编码基础, 需进一步进行概率分布建模、自适应学习等, 再度增加了算法的时空复杂性。当前, 通用、低复杂度的多光谱图像压缩算法更加受到各领域应用的青睐, 具备更强的理论和实用价值。例如, 在互联网传输和电子终端显示中, 基于DCT的JPEG编码一直占据静态图像压缩的主流地位。同样, 基于小波编码的硬件和软件实现也依然是遥感领域光谱图像压缩的最优选择^[1]。综上, 用于引导压缩各环节的失真准则关乎后续重建图像应用适应度的优劣, 遥感类光谱图像压缩没有考虑重建图像的色彩还原性能, 无法满足低比特率下场景色彩信息的高保真复现, 而保真的色彩再现性能恰恰是光谱图像正在产生革命性影响的色彩复制类工业生产中极为关键的应用指标。平均CIELAB色度误差超过5是绝大部分应用都无法接受的。

面向色彩再现的光谱图像压缩, 通常分为: 降维法、色度降维复合编码及通用低复杂度的WF-X编码等。降维法为主流算法, 包含了主成分分析^[5]、 LabPQR^[6]、 LabRGB^[7]、 LabW2P(-M)^[8]、 LabAB^[9]、 XYZXYZ、 XYZLMS^[10]等。此类算法只对光谱图像谱向去相关, 主要提取典型照明下场景的色度通道信息, 并在一定程度上提取(或忽略)不可视光谱信息。因此其专用性强, 压缩比低, 色度值与再现环境相关程度高, 泛化能力不足。为了解决压缩比低的问题, 文献^[11]结合了降维法与传统编码, 首先提取光谱图像的RGB图, 然后获取原图与RGB估计图间的残差图, 最后采用JPEG2000分别对其编码, 实现了优先传输色度值的基础上对光谱图像的无损和有损压缩。但是, 其特定的RGB通道限制了使用范围, 通用性较弱。为了解决通用性问题, 作者^[12]提出了面向色彩再现的低复杂度光谱图像压缩WF-APWS-RA, 其以色感应失真准则指导编码, 首先提取标准观察者感应部分光谱信息, 然后结合传统编码优先传输观察者感应数据, 进而逐渐补充不可视光谱数据码流。该方法由于仅借助标准观察者感应特性, 因此不可避免地无法充分去除在特定范围照明条件下图像的不可视冗余。然而, 在色彩再现领域, 特定照明场景下的光谱色彩管理通常较为常用, 且关注其光照稳定性。综上, 色彩再现类光谱图像压缩研究多集中在光谱维冗余去除方面, 无针对性编码方案, 尚缺少面向特定照明场景的通用低复杂度压缩。

本文针对现有光谱图像压缩存在的特定再现环境下不可视冗余去除不充分、通用性弱、复杂度高等问题, 研究了特定光照中基于色彩失真引导的压缩原理, 基于此设计了特定光照中基于视觉感知特性的通用低复杂度色彩高保真光谱图像压缩算法。算法可有效重建特定再现条件下的光谱色彩信息, 具有优秀的变光照色彩再现稳定性, 同时可兼顾提升光谱重建精度。

1 特定光照中基于色彩失真引导的光谱图像压缩原理

目前, 光谱图像编码多以光谱图像的非感知差异引导, 目标是最小化原始和重建光谱图像间的光谱均方误差(mean squared error, MSE)。为了降低重建光谱图像的颜色偏差, 首先考虑人类视觉感知到的颜色数据提取, 在此基础上建立基于色彩感知误差的光谱图像压缩原理。

1.1 光谱图像色彩分解环境的构建

观察条件的指定, 是人类视觉系统感知颜色的前提。故本文首先确定对实物光谱进行色彩分解的观察环境, 包括: 场景光源和观察者模型。对于场景光源, 本文采用单一或混合照明光源, 作为光谱再现的目标照明条件。在包含n种可能的特定照明光色彩再现环境中, 采用国际照明委员会(CIE)标准照明体A、 D65、 D50、 F2等, 分别代表相关色温约为2 856、 6 500、 5 000和4 150 K的白炽灯光、平均日光、中午日光以及冷白荧光灯照明等的光谱功率分布。选取D65为通用单一再现光源, 选取多种照明的算术平均功率分布作为混合再现光源。对于观察者模型, 本文选取CIE 1931 2° 颜色匹配函数建模标准观察者条件。

1.2 光谱图像色彩感知数据提取算子

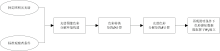
人类视觉系统基于观察环境对光谱进行解释, 进而感知到实物颜色。本文在感知意义下, 将光谱图像数据分为特定光照下的色彩基本刺激光谱和同色异谱黑。采用图1流程提取再现观察条件下的色彩感知数据, 设计色彩感知数据提取算子。

	Figure Option View Download New Window
	图1 再现观察条件下色彩感知数据提取算子形成流程图Fig.1 Flow chart of color perception data extraction operators

如图1所示, 在色彩分解环境下, 提取光照的相对功率分布S, 以及标准观察者的光谱三刺激值V, 由式(1)综合确定色彩转换矩阵D。

$D = diag ({[\begin{array}{l} \frac{1}{X_{ill}} & \frac{1}{Y_{ill}} & \frac{1}{Z_{ill}} \end{array}]}^{T}) VS$ (1)

式(1)中, [X_illY_illZ_ill]^T=VS· ones(1)。

色彩转换矩阵D可将实物光谱r从光谱空间转换至色彩三刺激值c, 即c=Dr。则色彩基本刺激光谱 $\bar{r}$ 可表示如式(2)

$\bar{r} = D^{T} (D D^{T})^{- 1} Dr = Rr$ (2)

式(2)中, R为本文光谱色彩分解矩阵。

基于色彩分解矩阵R, 鉴于压缩算法设计需求, 利用其对角元素, 设计特定再现照明条件下色彩感知数据提取算子W_S, 如式(3)。

$W_{S} = diag (sqrt (diag (R)))$ (3)

1.3 以特定光照中色彩感知误差为指导准则的图像压缩原理

小波图像嵌入编码, 是遥感领域流行的通用高效光谱图像压缩法, 其均以不依赖于人类感知的MSE作为引导压缩的图像失真准则。本节压缩原理借助该类通用压缩编码思想获得。

设光谱图像为F₃_d∈ R^M^×^N^×^L, 谱间子图为F_i∈ R^M^×^N, i=1, 2, …, L, 空间子图为F(x, y)∈ R^L, x=1, 2, …, M; y=1, 2, …, N。则均方误差可定义为

$MSE = \frac{1}{MNL} \sum_{i} \sum_{x} \sum_{y} (F_{i} (x, y) - {\hat{F}}_{i} {(x, y))}^{2}$ $= \frac{1}{MNL} \sum_{x} \sum_{y} ‖ F (x, y) - \hat{F} (x, y) ‖_{2}^{2}$ (4)

式(4)中, ${\hat{F}}_{\cdot}$ (· )表示重建光谱图像数据。

为降低人类对光谱图像的色彩感知偏差, 本文采用式(3)所示色彩感知数据提取算子, 建立式(5)特定光照中色彩感知误差指导准则。

$ε = \frac{1}{MNL} \sum_{x} \sum_{y} ‖ W_{S} F (x, y) - W_{S} \hat{F} (x, y) ‖_{2}^{2}$ $= \frac{1}{MNL} \sum_{r} ‖ W_{S} r - W_{S} \hat{r} ‖_{2}^{2}$ (5)

式(5)中, r为空间子图F(x, y), 即空间位置(x, y)处的实物光谱。由式(2)、式(3)和式(5)可知, 保证原始与重建光谱图像的特定光照色彩感知最大相似度, 即降低W_Sr偏差, 可有效降低Rr偏差, 从而降低光谱图像色彩基本刺激的损失。另外, 基于该压缩原理与W_S特性, 随着比特率的增加, 该类压缩可在优先降低色彩感知误差的同时, 逐渐补充同色异谱黑数据, 进而实现近无损压缩。

2 基于色彩感知的通用高保真光谱图像压缩方法W_SF-APWS-RA

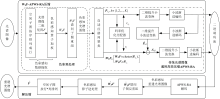
基于式(5)压缩准则, 分析式(4)可知, 利用传统编码对W_Sr进行编码, 可随比特率增加, 降低W_Sr数据的均方误差, 即 $MSE = (1 / MNL) \sum_{r} ‖ W_{S} r - \overset{\land}{W_{S} r} ‖_{2}^{2} 。$ 此时, 令色感知误差ε =MSE, 可得 $\hat{r}$ = $W_{S}^{- 1} \overset{\land}{W_{S} r}$ 。这表明, 在 $\hat{r}$ = $W_{S}^{- 1} \overset{\land}{W_{S} r}$ 的情况下, 可在W_Sr的渐进编码过程中, 逐渐降低重构光谱图像的特定光照色彩感知偏差。

故本文基于上述原理, 设计色彩感知算子加权、结合小波变换嵌入编码, 最终提出基于色彩感知的通用低复杂度色彩高保真光谱图像编解码器W_SF-APWS-RA。压缩和解压缩流程如图2所示, 其中, $P_{c_{k}}$ 为代表谱间子图^[12]。

	Figure Option View Download New Window
	图2 W_SF-APWS-RA压缩解压缩算法流程图Fig.2 Flow chart of W_SF-APWS-RA codec

2.1 光谱图像色彩预处理

如图2所示, 色彩预处理是实现色彩高保真重建的重要环节, 目标为生成色彩感知光谱图像。其包含三个步骤。首先, 光谱空间子图逐行(列)排列形成二维光谱矩阵F; 然后, 利用1.2节所提色彩感知数据提取算子W_S左乘F, 形成加权光谱图像二维矩阵W_SF, 实现对光谱图像的色彩感知数据提取; 最后, 对W_SF进行谱间子图重组, 以其行向量形成对应色彩感知光谱图像的各谱间子图。

色彩加权预处理, 相当于对光谱空间子图像素附加视觉感知权值, 对变换后的光谱相关数据进行嵌入编码, 有利于后续等比特率下基本色刺激的保留。设计的W_S矩阵为数值介于0-1间的对角阵, 较直接对F编码, W_SF数据提取了大部分光谱图像色彩感知数据, 具有更低的数量级, 利于编码存储, 且易于反向重建。而谱间子图重组为后续低复杂度的光谱图像数据去冗余提供了数据基础。因此, 该预处理步骤提取了色彩感知数据, 并形成了原理引导, 且利于进一步编码的加权光谱图像数据。

2.2 通用低复杂度的色彩感知数据空谱去冗余

由于色彩感知光谱图像的空谱特性类似原始光谱图像, 本文算法利用带间低复杂度AP聚类算法, 设计W_SF_i间负的F范数为色彩感知光谱图像谱间相似性度量, 形成感知光谱图像谱间较优稀疏表示, 将其变换为代表谱间子图和差别子图, 有效去除代表大部分基本色刺激的加权图像中的谱间相关性。对于代表子图 $P_{c_{k}}$ 和差别子图Δ '_jk, 算法采用通用二维提升小波变换转换至小波空间, 利用渐进编码SPIHT进行二维小波变换系数编码, 有效去除空间相关性及结构冗余。

一维谱段间聚类与二维小波变换及编码的结合, 并未涉及高维特征变换编码, 因此可以避免计算复杂度高的问题。另外, 基于代表大部分基本色刺激的加权光谱图像进行变换, 可以直接消除光谱图像的感知冗余, 有效去除不可视成分。

2.3 低复杂度下的性能提升策略

为进一步提升编码性能, 本文算法按需分配码率, 并补偿子图的量化误差。对于W_SF各谱间稀疏表示成分的编码, 设计码率优化分配器, 采用基于谱间代表子图-差别子图信息量的码率预分配策略, 对信息量较大的代表子图分配较多的比特数, 反之分配较少比特, 合理控制利用了比特率。对于类内差别子图编码, 采用预测差别子图编码, 以补偿谱间代表子图编码产生的误差。

两种性能提升策略, 利用单波段标准差或矩阵相减运算即可, 均简单易行, 可在低复杂度下有效提升感知数据重构质量, 进一步增强光谱图像的重建精度。

3 算法验证

为验证所提算法有效性, 本文采用单一和混合再现光源色彩感知算子, 分别形成算法W_SdF-APWS-RA和W_SfF-APWS-RA, 并选取哥伦比亚大学发布的色彩涵盖全面、纹理渐增的三幅光谱图像, 从光谱重建和色彩再现精度两个方面, 与通用低复杂度的APWS、 APWS-RA及色彩再现类WF-APWS-RA压缩算法进行对比实验。测试光谱图像共31波段(波长范围: 400~700 nm, 光谱分辨率: 10 nm, 空间分辨率: 512× 512), 量化位数16 bit, 其D65下对应RGB图如图3。

	Figure Option View Download New Window
	图3 多光谱图像合成RGB图 (a): 多光谱玩具图; (b): 多光谱羽毛图; (c): 多光谱衣物图Fig.3 Composite RGB images of multispectral images (a): Stuffedtoys; (b): Feathers; (c): Cloth

3.1 光谱重建精度

本文采用峰值信噪比(peak signal to noise ratio, PSNR)评价重建光谱图像的光谱精度, 其公式为 $PSNR＝ (1 / L) \sum_{i}\left(10 \log _{10}\left[\left(2^{16}-1\right)^{2} / M S E_{i}\right]\right) $。其中, $L$为波段数, $M S E_{i}=[1 /(M N)] \sum_{x} \sum_{y}\left(\boldsymbol{F}_{i}(x, y)-\hat{\boldsymbol{F}}_{i}(x, y)\right)^{2}$为单波段均方误差, F_i(x, y)与 ${\hat{F}}_{i}$ (x, y)分别为场景于第i波段(x, y)处的原始与重建光谱反射率。算法的光谱重建性能对比如图4所示。

	Figure Option View Download New Window
	图4 测试图像在不同通用低复杂度压缩算法下的PSNR性能对比 (a): 多光谱玩具图; (b): 多光谱羽毛图; (c): 多光谱衣物图Fig.4 PSNR performance comparison for test images under various universal low-complexity compression (a): Stuffedtoys; (b): Feathers; (c): Cloth

由图4可知, 本文方法W_SfF-APWS-RA(复合光源)的PSNR重建性能优于W_SdF-APWS-RA(单一光源), 均优于通用色彩再现压缩WF-APWS-RA。随着图像纹理细节的增多, 本文算法PSNR逐渐从低中高比特率下, 全面超越APWS算法, 鲁棒性较好。 APWS-RA的光谱重建性能最优, 但纹理内容越复杂, 本文方法与APWS-RA的PSNR差距越小。

对于stuffedtoys, 较WF-APWS-RA, 在0.1、 0.2、 0.5、 0.8和1 bpppb比特率下, W_SfF-APWS-RA和W_SdF-APWS-RA的平均PSNR分别提升了0.90和0.81 dB; 当压缩比为20和32时, W_SfF-APWS-RA的PSNR最低和最高分别提升了0.75和1.06 dB; 当压缩比为20和160时, W_SdF-APWS-RA的PSNR最低和最高分别提升了0.69和0.95 dB。对于feathers, W_SfF-APWS-RA和W_SdF-APWS-RA的平均PSNR分别提升了0.79和0.61 dB; 当压缩比为160和32时, W_SfF-APWS-RA的PSNR最低和最高分别提升了0.67和0.93 dB, W_SdF-APWS-RA分别提升了0.52和0.75 dB。对于cloth, W_SfF-APWS-RA和W_SdF-APWS-RA的平均PSNR分别提升了0.68和0.27 dB; 当压缩比为160和16时, W_SfF-APWS-RA的PSNR最低和最高分别提升了0.35和0.94 dB, W_SdF-APWS-RA分别提升了0.05和0.55 dB。另外, 色彩全面条件下, 细节纹理复杂程度越低, 本方法PSNR越高; 且随着比特率的提升, 本方法的重建PSNR逐渐提高, 可实现渐进式无损压缩。

3.2 色彩再现精度

本文采用平均和最大色度误差衡量方法的色彩保真性能, 采用不同照明下色度误差的标准差衡量算法的色彩再现稳定性。在特定再现条件下的色度误差定义为 $Δ E_{ab}^{*} = \sqrt[]{(Δ L^{*})^{2} + (Δ a^{*})^{2} + (Δ b^{*})^{2}} 。式中, Δ L^{*} 、 Δ a^{*} 、 Δ b^{*}$ 为原始和重建光谱图在均匀色度空间CIELAB中对应的三个维度距离。色彩再现稳定性的量值定义为 $s = \sqrt[]{\sum_{i = 1}^{n} (Δ E_{ab_i}^{*} {- \overset{E_{ab}^{*}}{Δ})}^{2} / (n - 1)}$ , 其中, $n$ 为不同照明数目, $Δ E_{ab_i}^{*}$ 为重建图像在第i种照明下的色度误差(平均/最大), $\overline{\Delta E_{a b}^{*}}=\left(\sum_{i=1}^{n} \Delta E_{a b_{-} i}^{*}\right) / n$为重建图像在 $n$ 种不同照明下的平均色差。算法色彩重建性能客观对比如表1— 表4所示。

表1 多光谱玩具图, 不同观察条件下各算法的重建图色彩失真对比 Table 1 Δ

E_{ab}^{*}

performance comparison of stuffedtoys under different illumination

压缩算法	不同照明条件下色差比较(平均/最大色差)
	0.1 bpppb			0.5 bpppb			1 bpppb
	D65	A	F2	D65	A	F2	D65	A	F2
APWS	4.35/70.83	4.40/69.37	4.40/67.96	1.66/27.31	1.72/29.22	1.90/33.67	1.40/17.93	1.48/18.07	1.70/20.41
APWS-RA	2.48/41.59	2.51/37.34	2.45/37.12	0.77/26.13	0.73/20.13	0.76/23.49	0.60/16.77	0.57/15.46	0.59/17.41
WF-APWS-RA	3.17/58.50	3.24/62.53	2.79/45.08	0.92/24.19	0.96/22.77	0.79/21.12	0.61/15.61	0.63/11.92	0.53/11.16
W_SdF-APWS-RA	2.30/36.22	2.49/53.62	2.22/41.37	0.71/14.10	0.77/14.61	0.66/12.79	0.50/9.60	0.52/8.53	0.46/8.53
W_SfF-APWS-RA	2.37/38.20	2.46/54.34	2.27/36.35	0.72/18.35	0.74/15.97	0.69/19.32	0.51/12.03	0.51/9.88	0.51/15.67

表1 多光谱玩具图, 不同观察条件下各算法的重建图色彩失真对比 Table 1 Δ

E_{ab}^{*}

performance comparison of stuffedtoys under different illumination

表2 多光谱羽毛图, 不同观察条件下各算法的重建图色彩失真对比 Table 2 Δ

E_{ab}^{*}

performance comparison of feathers under different illumination

压缩算法	不同照明条件下色差比较(平均/最大色差)
	0.1 bpppb			0.5 bpppb			1 bpppb
	D65	A	F2	D65	A	F2	D65	A	F2
APWS	5.76/219.27	5.80/194.77	5.79/219.36	2.62/28.17	2.70/31.88	2.91/38.17	2.10/42.69	2.22/46.87	2.46/55.70
APWS-RA	3.54/71.11	3.52/60.05	3.36/68.01	1.19/33.65	1.16/30.70	1.15/33.37	0.77/20.24	0.77/17.58	0.76/20.02
WF-APWS-RA	3.63/93.11	3.75/84.14	3.41/85.37	1.21/30.93	1.28/28.66	1.12/29.41	0.72/13.12	0.78/14.91	0.68/17.15
W_SdF-APWS-RA	3.38/71.64	3.46/66.41	3.27/73.40	1.14/24.01	1.15/23.45	1.09/29.20	0.69/12.13	0.70/11.78	0.68/13.22
W_SfF-APWS-RA	3.37/72.04	3.39/66.82	3.24/74.30	1.14/25.68	1.12/24.22	1.08/28.56	0.69/12.53	0.68/9.72	0.67/13.36

表2 多光谱羽毛图, 不同观察条件下各算法的重建图色彩失真对比 Table 2 Δ

E_{ab}^{*}

performance comparison of feathers under different illumination

表3 多光谱衣物图, 不同观察条件下各算法的重建图色彩失真对比 Table 3 Δ

E_{ab}^{*}

performance comparison of cloth under different illumination

压缩算法	不同照明条件下色差比较(平均/最大色差)
	0.1 bpppb			0.5 bpppb			1 bpppb
	D65	A	F2	D65	A	F2	D65	A	F2
APWS	9.95/272.03	9.23/299.37	9.53/204.37	5.17/119.52	4.76/102.86	4.93/98.11	2.96/46.03	2.74/35.78	2.85/39.37
APWS-RA	9.62/195.17	8.91/152.81	9.16/159.17	3.84/64.68	3.52/52.29	3.69/56.69	1.92/37.69	1.73/29.61	1.93/33.32
WF-APWS-RA	8.26/182.32	7.16/135.17	7.67/122.23	3.09/57.32	2.68/40.11	2.65/45.75	1.53/27.45	1.36/24.27	1.20/22.59
W_SdF-APWS-RA	8.00/186.16	7.27/172.92	7.70/176.38	2.96/40.64	2.76/31.16	2.81/34.95	1.34/27.99	1.26/26.45	1.24/29.65
W_SfF-APWS-RA	7.80/235.32	7.09/193.04	7.48/197.61	2.75/41.98	2.57/39.97	2.59/34.30	1.24/27.75	1.16/21.94	1.13/21.01

表3 多光谱衣物图, 不同观察条件下各算法的重建图色彩失真对比 Table 3 Δ

E_{ab}^{*}

performance comparison of cloth under different illumination

表4 色彩重建统计性能对比 Table 4 Color reproduction statistical performance comparison

平均色差是衡量色彩重建性能的重要指标。由表1— 表3可知, APWS平均色差最大, WF-APWS-RA会随着图像色彩纹理以及比特率的增加, 色彩重建性能逐渐全面超越APWS-RA。本文算法为四种算法中最优: W_SdF-APWS-RA更适合色彩纹理复杂度低中的stuffedtoys和feathers, 对于复杂度高的cloth, 算法优先保证了D65下的色彩重建性能, 并随着比特率的提升, 平均色差逐渐降低, 适应了更多照明再现环境; W_SfF-APWS-RA适应于色彩纹理复杂度低中高的所有图像, 对于复杂度中高的feathers和cloth绝对最优, 较APWS、 APWS-RA和WF-APWS-RA, 最高提升可达47.44%、 29.76%和10.95%。

由表4知, APWS、 APWS-RA和WF-APWS-RA的色彩重建精度依次提升。本文方法较其他算法, 在0.1、 0.5和1 bpppb时, 于各个光照下的平均色差均值最低: W_SdF-APWS-RA算法在三种光照下的平均色差均值分别为4.45、 1.56和0.82, 较其余三种算法中最优的WF-APWS-RA, 误差分别降低了6.94%, 4.42%和8.08%; W_SfF-APWS-RA的平均平均色差均值分别为4.39、 1.49和0.79, 较WF-APWS-RA误差分别降低了8.38%、 8.84%和11.69%。由稳定性统计数据可知, 本文方法具有更优更稳定的变光照色彩再现性能。随着比特率的提升, W_SfF-APWS-RA的平均色差稳定性逐渐超过W_SdF-APWS-RA, 提升更快。另外, 值得注意的是, 在160倍压缩比下, 两种算法的统计平均色差均可控制在5以内, 可更好地满足工业、文化遗产等领域需求。同理, 对于最大色差, 本文算法同样可达综合最优。

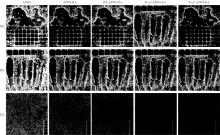
为进一步体现客观指标数值差异, 对算法色彩再现性能进行主观评价, 将五种算法在160倍(stuffedtoys和feathers)和16倍(cloth)压缩比下的代表性重建光谱图像于D65下进行直观RGB色彩再现效果对比, 如图5所示。此外, 以图6展示上述代表性重建光谱图在D65下产生的CIELAB色度偏差, 其中大于5的色差被放大至255, 以突出显示其分布情况。原测试光谱图像在D65下的再现RGB图如图3。

Figure Option
View Download New Window

图5 不同压缩比下, APWS、 APWS-RA、 WF-APWS-RA、 W_SdF-APWS-RA和W_SfF-APWS-RA算法重建图的RGB色彩再现效果对比
(a): Stuffedtoys, 0.1 bpppb; (b): Feathers, 0.1 bpppb; (c): Cloth, 1 bpppbFig.5 RGB color reproduction comparison of reconstructed images of APWS, APWS-RA, WF-APWS-RA, W_SdF-APWS-RA and W_SfF-APWS-RA algorithms under different compression ratios
(a): Stuffedtoys, 0.1 bpppb; (b): Feathers, 0.1 bpppb; (c): Cloth, 1 bpppb

Figure Option
View Download New Window

图6 不同压缩比下, APWS、 APWS-RA、 WF-APWS-RA、 W_SdF-APWS-RA和W_SfF-APWS-RA算法重建图于D65下的CIELAB色差分布对比
(a): Stuffedtoys, 0.1 bpppb; (b): Feathers, 0.1 bpppb; (c): Cloth, 1 bpppbFig.6 CIELAB color difference distribution comparison of reconstructed images of APWS, APWS-RA, WF-APWS-RA, W_SdF-APWS-RA and W_SfF-APWS-RA algorithms at different compression ratios under D65
(a): Stuffedtoys, 0.1 bpppb; (b): Feathers, 0.1 bpppb; (c): Cloth, 1 bpppb

由图5和图6, 结合表1— 表3可知, 随着比特率的提升, 各算法的重建色差逐步降低, 本文算法可更快地达到更小的色差, 呈现更稀疏零星的5以上色差分布。在相同比特率下, 较其他算法, 本文W_SdF-APWS-RA和W_SfF-APWS-RA算法(4、 5列)直接提升了色观感, 产生的色差较小, 5以上的CIELAB色差分布区域(图6中白色区域)减少, 在视觉上实现了明显的色彩再现质量提升。对于stuffedtoys, 对比图5(a)和图6(a)各列可知, 在160倍压缩比下, 本文算法较APWS、 APWS-RA和WF-APWS-RA算法, 消除了重建时产生的大量边界模糊和横竖条纹现象, 很好地降低了点状和带状色彩失真, 实现了光谱重建质量的提升。从图5(a)的上部分玩具边缘及背景区域对比可知, 较其他算法, 本文算法的重建RGB图像边缘整体更加清晰, 蓝色玩具胸前的点状失真、红色玩具翅膀底端的带状失真及背景部分的带状失真得到明显降低(其余位置可参照图6色差分布区域, 与图5进行对照观察); 从下部分色卡及背景区域对比可知, 本文算法再现图像的色块区域色彩更加柔和平滑, 色块间隔更具区分度, 色卡上部边缘清晰, 色卡下部文字及背景部分降低了带状色差, 整体色彩呈现及过渡更加细腻、平缓。同理, 对于feathers, 由图5(b)和图6(b)可知, 在160倍压缩比下, 本文算法在色卡四周、羽毛内部及羽毛根部等区域均较好地降低了色彩失真。对于cloth, 由图5(c)和图6(c)可知, 在16倍压缩比下, 本文算法消除了众多花朵轮廓、色卡边缘及纹样内部的点状色彩失真。

综上所提两种算法具有最优的重建色彩精度和次优的光谱精度。随着图像色彩丰富程度和细节纹理的增加, W_SfF-APWS-RA算法的综合性能较W_SdF-APWS-RA算法更胜一筹, 适用范围更广。

4 结论

本文以特定范围光照中光谱图像的高再现色彩质量作为压缩目标, 提出色彩感知数据提取算子, 并基于此设计了以特定光照中色彩感知误差为引导的W_SfF-APWS-RA和W_SdF-APWS-RA压缩方法。算法较现有色彩再现领域的经典降维压缩, 压缩比可调, 通用性强, 在不同比特率下色彩信息优先保存, 不可视部分光谱信息可渐进存储。较现有通用光谱图像压缩, 本文方法提取了特定光照范围下光谱图像的色彩感知数据, 进行了充分的指定条件下不可视冗余的去除, 采用一维谱间聚类结合二维小波变换去除空谱冗余, 并利用二维编码器编码, 不需要高维特征提取及编码, 保留了算法通用与低复杂度的优势, 具有更优的色彩重建精度、变光照色彩再现稳定性及光谱重建精度。

参考文献

文献列表

[1]	Hernández-Cabronero M, Kiely A B, Klimesh M, et al. IEEE Geoscience and Remote Sensing Magazine, 2021, 9(4): 102. [本文引用:2]
[2]	Prakash A, Moran N, Garber S, et al. Semantic Perceptual Image Compression Using Deep Convolution Networks. 2017 Data Compression Conference (DCC), 2017, 250. [本文引用:1]
[3]	Kong F, Hu K, Li Y, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 2745. [本文引用:1]
[4]	Guo Y, Tao Y, Chong Y, et al. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 1. [本文引用:1]
[5]	Ma L, Qiu X, Cong Y. MIPPR 2015: Multispectral Image Acquisition, Processing, and Analysis, 2015, 9811: 98110C. [本文引用:1]
[6]	Wu G, Liu Z, Yang S, et al. Journal of Spectroscopy, 2014, 2014(1): 595602. [本文引用:1]
[7]	Lv C, Li C, Xiao K, et al. Optics Express, 2022, 30(22): 40144. [本文引用:1]
[8]	Liang W, Hao W, Jin H, et al. Spectroscopy Letters, 2021, 54(5): 395. [本文引用:1]
[9]	Le Moan S, Blahová J, Urban P, et al. Journal of Imaging Science and Technology, 2016, 60(6): 060501. [本文引用:1]
[10]	Zhang X, Wang Q, Wang Y, et al. Optics Letters, 2012, 37(24): 5097. [本文引用:1]
[11]	Shinoda K, Murakami Y, Yamaguchi M, et al. Journal of Electronic Imaging, 2011, 20(2): 023003. [本文引用:1]
[12]	LIANG Wei, ZENG Ping, LUO Xue-mei, et al(梁玮, 曾平, 罗雪梅, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(1): 276. [本文引用:2]

2021

0.0

... 目前, 光谱图像压缩集中应用于航空航天遥感, 通常包含三个处理阶段: 压缩指导准则、去相关性以及编码^[1] ...

... 同样, 基于小波编码的硬件和软件实现也依然是遥感领域光谱图像压缩的最优选择^[1] ...

2017

0.0

... 随着深度学习在计算机视觉任务中的兴起, AEs、 VAEs、 CNNs、 RNNs、 GANs等网络架构先后应用于静态色度图像压缩^[2,3,4] ...

2022

0.0

... 随着深度学习在计算机视觉任务中的兴起, AEs、 VAEs、 CNNs、 RNNs、 GANs等网络架构先后应用于静态色度图像压缩^[2,3,4] ...

2023

0.0

... 随着深度学习在计算机视觉任务中的兴起, AEs、 VAEs、 CNNs、 RNNs、 GANs等网络架构先后应用于静态色度图像压缩^[2,3,4] ...

2015

0.0