基于近红外光谱技术的木糖含量快速检测

引用本文

蓝希华, 王志国, 栾小丽, 刘飞. 基于近红外光谱技术的木糖含量快速检测[J]. 光谱学与光谱分析, 2025,45(7): 1916-.
LAN Xi-hua, WANG Zhi-guo, LUAN Xiao-li, LIU Fei. Rapid Detection for Xylose Content Using Near-Infrared Spectroscopy Technology[J]. Spectroscopy and Spectral Analysis, 2025,45(7): 1916-.
Doi:10.3964/j.issn.1000-0593(2025)07-1916-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于近红外光谱技术的木糖含量快速检测

蓝希华, 王志国^*, 栾小丽, 刘飞

江南大学自动化研究所轻工过程先进控制教育部重点实验室, 江苏无锡 214122

*通讯作者 e-mail: zhiguowang@jiangnan.edu.cn

作者简介: 蓝希华, 1998年生,江南大学轻工过程先进控制教育部重点实验室硕士研究生 e-mail: 6221913030@stu.jiangnan.edu.cn

收稿日期: 2024-08-07 修回日期: 2025-03-03 接受日期: 2025-03-03

基金: 国家自然科学基金重点项目(61833007)资助

摘要

木糖作为一种功能性低聚糖, 具有抗氧化、促进肠道健康等保健作用, 被广泛应用于食品、医药和生物燃料等领域。目前仍然缺乏有效的木糖含量快速检测方法。针对木糖生产过程中的含量检测问题, 提出一种基于近红外光谱的在线检测方法。首先, 采集样本溶液, 使用近红外光谱仪扫描得到原始光谱, 进一步使用一阶导数和平滑滤波方法对原始光谱进行预处理, 去除噪声与基线漂移的影响。然后, 使用随机蛙跳算法对光谱变量进行特征选择, 结合预测相对分析误差搜索最佳特征数, 结果显示: 当特征数在20~30时模型的预测性能最优。综合其他指标, 选择特征数量为25, 确定能表征木糖含量的波长特征。由于随机蛙跳算法具有随机子集选择和随机森林回归的特性, 该算法在执行高维木糖数据的特征波长筛选任务时存在明显优势, 同时也存在结果重现性低的缺陷。在得到波长特征后对结果进行加权累计, 弱化该算法不确定性对最终模型的影响, 再以液相色谱仪测得的数据为标签, 建立木糖含量的预测模型。最后, 使用以上方法对工艺现场采集的样本进行木糖含量的快速测定, 并对比PLS模型及Lasso模型的预测效果。结果表明, 指标中的训练集决定系数 R²=0.937 7, 测试集决定系数$R_{p}^{2}=0.933 5$, R²和$R_{p}^{2}$都接近1, 模型能较好的解释训练集数据, 并具备良好的泛化性能。预测均方根误差RMSEP=5.844 6, 预测相对分析误差RPD=3.879 2>2.5, 模型可以较为准确地预测样品的木糖含量。通过对比发现, RJFA-PLS模型的各项评价指标均优于PLS模型, RMSEP降低了112.7%, R²、 RPD和$R_{p}^{2}$分别提高了21.8%、 52.5%和24.6%。而Lasso算法在基于本数据集的木糖含量预测上表现不佳。在此次实验条件下, 使用以上方法建立的模型比PLS模型及Lasso模型更适用于木糖含量的预测。本方法解决了木糖含量检测结果滞后的问题, 还为木糖在线检测技术的研究提供了先决条件。

关键词: 木糖含量; 近红外光谱; 随机跳蛙算法; 快速测定

中图分类号:O657.3 文献标志码:A

Rapid Detection for Xylose Content Using Near-Infrared Spectroscopy Technology

LAN Xi-hua, WANG Zhi-guo^*, LUAN Xiao-li, LIU Fei

Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, Jiangnan University, Wuxi 214122, China

*Corresponding author

Abstract

Xylose, as a functional oligosaccharide, possesses health benefits such as antioxidant properties and promoting intestinal health, and is widely used in food, medicine, and biofuels. There is still a lack of effective rapid detection methods for xylose content. An online detection method based on near-infrared spectroscopy technology is proposed to address the issue of content detection during xylose production. Firstly, sample solutions are collected and scanned using a near-infrared spectrometer to obtain raw spectra. The raw spectra are then preprocessed using first derivative and smoothing filter methods to remove noise and baseline drift effects. Subsequently, the random frog algorithm is employed for feature selection of spectral variables, and the prediction relative analysis error is used to search for the optimal number of features. The results show that the model's predictive performance is optimal when the number of features is between 20 and 30. Considering other indicators, the number of features is selected as 25, determining the wavelength characteristics representing xylose content. Due to the random subset selection and random forest regression characteristics of the random frog algorithm, this algorithm has obvious advantages in performing the task of feature wavelength screening for high-dimensional xylose data, but also has the defect of low result reproducibility. After obtaining the wavelength features, the results are weighted and accumulated to weaken the impact of the algorithm's uncertainty on the final model. Then, a predictive model for xylose content is established using data measured by a liquid chromatograph as labels. Finally, the method is used to rapidly determine the xylose content of samples collected from the process site, and the prediction effects are compared with those of the PLS and Lasso models. The results indicate that the training set determination coefficient R²=0.937 7, and the test set determination coefficient $R_{p}^{2}=0.933 5$, with R² and $R_{p}^{2}$ close to 1, indicating that the model can explain the training set data well and has good generalization performance. The prediction root mean square error RMSEP=5.844 6, and the prediction relative analysis error RPD=3.879 2>2.5, indicating that the model can predict the xylose content of samples relatively accurately. Through comparison, it is found that the RJFA-PLS model's evaluation indicators are superior to those of the PLS model, with RMSEP reduced by 112.7%, and R², RPD, and $R_{p}^{2}$ increased by 21.8%, 52.5%, and 24.6%, respectively. However, the Lasso algorithm performs poorly predicting xylose content based on this dataset. Under the experimental conditions of this study, the model established using the above method is more suitable for predicting xylose content than the PLS and Lasso models. The proposal of this method solves the problem of lag in xylose content detection results and also provides a prerequisite for the research of online detection technology for xylose.

Keyword: Xylose content; Near infrared spectroscopy; Random jumping frog algorithm; Rapid determination

文章图片

引言

木糖作为一种功能性低聚糖, 因其安全无毒、不被肠道吸收从而避免引起肥胖、可促进人体肠道益生菌生长等优点, 被广泛用于食品、饲料和医药等领域。实际工业过程中, 木糖的分离提纯主要设备之一是模拟移动床。为保证模拟移动床设备的正常运行, 操作人员需要对各出口的产物含量进行检测。木糖含量的传统测量方法是使用高效液相色谱仪进行测定。该方法操作和分析过程依赖专业技术人员, 分析时间过长, 且色谱柱寿命有限。近红外(near-infrared, NIR)光谱检测技术是一种通过检测分子化学键的特定频率吸收来分析物质成分的方法, 利用分子吸收固定频率的光子实现能级跃迁, 其具有快速性、低成本等特点。

近红外光谱技术应用于各行业的在线检测, 取得了良好效果, 其中较常见的应用领域有化工、食品和农业。早在20世纪90年代, 近红外分析技术就被应用于化工领域, 用于建立多元回归模型, 在线分析混合物中乙烷、乙烯、丙烷和丙烯的含量。随后, Tang等将近红外光谱分析技术应用于流化床系统的控制, 利用探头对流化床一步制粒的全过程进行扫描采集光谱, 建立预测模型后, 使用该模型得到的温度和水分数据作为流化床干燥终点的判定条件, 为干燥终点的多变量控制提供了一种新思路^[1]; Yang等提出基于光纤近红外透射光谱的新分析方法, 对中药大孔吸附树脂纯化过程进行检测, 并成功地用于黄连生物碱提纯过程^[2]。

在食品和农业领域, Lafuente等将声波脉冲和近红外光谱两种非破坏分析技术相结合, 提高了桃品种“ Calrico” 的MT硬度检测的可靠性^[3]。 Mishra等采集苹果的光谱数据, 尝试使用动态正交化投影和域自适应两种方法对苹果的无损糖分检测模型进行校正, 两种尝试均取得成功^[4]。近红外技术还被用于食品质量检测中, Dharmawan等完成了主成分分析(PAC)和机器学习算法的光谱技术开发工作, 并将该项技术用于检测咖啡豆来源^[5]; Cruz-Tirado等尝试使用近红外技术鉴别羊驼肉中掺入其他肉的行为, 取得良好效果^[6]; Zhao等使用近红外分析结合化学计量方法实现高粱单宁含量的快速检测^[7]; Xu等采集水稻节间样本, 构建水稻节间主要碳氮代谢组分模型, 为水稻栽培研究提供支撑^[8]; Jia等为了减少光谱仪购入成本, 将低分辨率光谱数据优化, 分辨霉变小麦, 并取得成功^[9]; Tang等采集柚子透射光谱数据, 在有限波长范围内建立近红外模型, 实现了柚子糖度的在线检测^[10]。

近红外检测技术还应用于其他的领域, 如能源与环境领域。 Felizardo等使用NIR开发校准模型, 并在模型建立之前, 采用一阶Savitsky-Golay导数、二阶Savitsky-Golay导数和标准正态变换(SNV)等预处理方法对原始光谱数据进行预处理, 使模型的预测性能得到提升^[11]。 Kulcsar等将近红外在线分析仪与偏最小二乘(PLS)相结合, 建立基于PLS的二维近红外光谱模型, 并将该模型应用于发动机缸的在线过程监控^[12]。 Yang等使用漫反射近红外光谱仪扫描水泥生料, 采用X射线荧光光谱法标定参考值从而建立近红外光谱模型, 实现了水泥生料中氧化物含量的快速测定^[13]。 Nioka等将近红外光谱技术应用于医学领域, 使用近红外窗口检测血液来定位癌症^[14]。

本研究提出了一种基于近红外光谱技术的木糖含量快速检测方法。得到原始光谱数据后, 先用一阶导数(FD)和平滑滤波(SG)方法对数据进行预处理, 再使用随机蛙跳算法(RJFA)对全光谱进行特征选择, 筛选出与木糖含量强相关的特征波长, 为了解决RJFA筛选特征波长具有不确定性的问题, 对得到的特征波长进行加权累计后再进行木糖含量预测模型的建立, 并将得到的RJFA-PLS模型与PLS模型和Lasso模型作对比, 结果显示本研究建立的预测模型的预测性能和泛化能力均优于PLS模型与Lasso模型。

1 实验部分

1.1 仪器与样品

实验仪器采用Bruker Optics公司生产的Matrix-F近红外光谱仪, 配套软件为OPUS/QUANT。实验样品采集自木糖分离提纯的色谱分离工艺现场, 生产原料为发酵后的木糖母液, 洗脱液为纯净水, 工艺生产温度为70 ℃。木糖分离提纯工艺采用液相色谱法, 通过不同的流动相和固定相的相互作用, 分离出木糖、果糖、阿拉伯糖等成分。该工艺通过有效分离和提纯, 从混合液中获得高纯度的木糖, 为后续生产提供原料。在一个完整的木糖分离提纯过程中按时间均匀采集20个样本, 一共采集7个生产过程中的样本, 总计样本140个。

1.2 光谱数据采集

近红外光波长范围为780~2 526 nm, 在该范围的光谱吸收主要由含氢基团的倍频和合频引起。木糖别名为五碳醛基糖, 化学式为C₅H₁₀O₅, 具有碳氢键(C— H)、碳氧键(C— O)、氢氧键(O— H)三种化学键。而该三种化学键在近红外光谱频段都具有吸收峰, 故使用近红外光谱信息检测木糖含量在理论上具有可行性。当特定频率的光以固定光程通过样本溶液时, 样本溶液中的物质分子吸收该频率的光子发生能级跃迁, 同时透射光的强度降低, 在谱图上表现为吸收峰。当物质浓度越高时, 透射光的损失越大, 光强越低。根据Beer-Lambert定律可知物质特定波长处的吸光度与物质浓度成正比。

$A = ε \times c \times L$ (1)

式(1)中, A为吸光度, c为物质浓度, L为光程, ε 为吸光系数。由于式(1)只表示吸光度A与物质浓度c呈正相关, 为了解释吸光度A与物质含量的联系, 需要建立物质浓度c与物质含量之间的关系: 当溶液总体积和总质量恒定, 物质浓度和含量呈正相关, 所以对于同一份溶液, 当特定物质的含量增加时, 特定频率的光的吸光度也将增加, 物质含量与吸收度也存在如式(1)所示的正相关性。

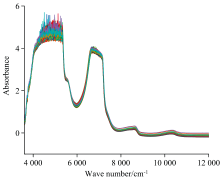
设置光谱仪的波长扫描范围为800~2 500 nm, 光谱仪分辨率设为8 cm^-1, 扫描时间为16 s, 扫描次数为20次。将采集得到的样本分别取5 mL用光谱仪进行扫描, 得到近红外光谱原始数据。为尽量减少测量误差, 数据采集时将同一样本扫描两次, 取其吸光度平均值作为原始光谱数据, 如图1 所示。为了确保两次扫描数据的一致性和可靠性, 在每次扫描后, 对比两次测量的吸光度值。如果两次数据的差异小于0.02吸收度单位, 则认为数据合理, 并取其平均值作为最终光谱数据。如果两次扫描数据差异较大, 则进行第三次扫描, 若第三次扫描与前两次中某一次的数据一致, 则取相同两次结果的平均值作为最终结果; 若差异仍未得到有效控制, 则排除该样本数据并重新采样。另外各取30 mL样品, 使用高效液相色谱法得到样品溶液中的木糖含量。

	Figure Option View Download New Window
	图1 样本原始吸收光谱Fig.1 The original absorption spectra of the samples

采集得到的原始光谱数据如图1所示, 每条曲线代表一个样本的吸收谱数据, 每个样本数据都由2 125个波长变量的吸光度组成。由于C— O键、 O— H键和C— H键伸缩振动组合频率相近, 在约4 320~5 300 cm^-1处形成一个宽峰, O— H键伸缩振动二倍频在约6 900~7 100 cm^-1处形成一个吸收峰, C— H键和O— H键伸缩振动三倍频在8 400~8 700 cm^-1处和10 200~10 600 cm^-1处形成两个吸收峰。

1.3 数据预处理

样本在进行近红外光谱数据采集时会受到各种因素的干扰导致基线漂移, 同时不可避免的产生随机噪声, 因为数据本身不均匀的原因还会产生基线漂移, 采集得到的数据会因为尺度差异过大而对后续的模型产生不利影响。选择合适的预处理方法能够极大程度解决以上问题, 突出光谱特征信息, 提高信噪比。

常见的近红外预处理方法大致分为四类, 分别为基线校正、散射校正、平滑处理和尺度放缩。基线校正方法如FD, 能够消除基线漂移的影响。散射校正方法如多元散射校正(MSC)和SNV, 用来处理样品颗粒大小、形状、分布不均匀导致的影响。平滑处理方法如SG、移动平均平滑(MA)可以用来消除光谱数据中的随机噪声。尺度放缩方法如最大最小归一化(MMS)、均值中心化(CT)、标准化(SS)主要用于去除量纲, 消除不同变量因为数值大小差异过大对模型建立产生的不利影响。

1.4 特征波长选择

前面采集到的原始光谱数据中仅存在少部分与木糖含量有关的特征波长, 使用全谱数据建立预测模型泛化性能低, 且易受到无关变量的影响。建模前首先对光谱数据进行特征波长选择, 减少数据维度非常必要。传统的波长选择方法主要包括逐步回归、区间偏最小二乘回归和主成分分析等。这些方法能够有效筛选出与目标变量相关的波长, 从而提高模型的预测性能。然而逐步回归容易受多重共线性的影响, 导致波长选择结果不稳定; 区间偏最小二乘对区间划分的依赖性大, 不合理的区间划分可能导致模型性能下降, 人为调整区间划分方式又会导致该方法的效率大幅度降低; 主成分分析作为无监督学习方法可能会忽略与目标变量相关的重要波长。

为克服传统方法的不足, 采用随机蛙跳算法(RJFA)进行特征波长选择。 RJFA结合了随机子集选择和随机森林回归的特性, 使其能够在广泛的特征空间中进行全局搜索, 适用于处理木糖含量预测中的高维光谱数据。在此研究中, 随机子集选择特性帮助算法在高维数据中避免冗余和不相关特征的干扰, 提高了特征选择的稳定性和准确性。随机森林回归则通过集成多个回归模型, 增强了预测性能和鲁棒性。通过对选定特征波长进行加权累计, 进一步减少了不确定性对最终模型的影响。相比传统方法, RJFA具有更强的适应性和更高的效率, 能够在较大的搜索空间内找到最优特征组合, 减少共线性对模型的影响, 从而提升模型的预测精度和泛化能力。

RJFA具体实现步骤如下:

(1) 从全集V中随机选择Q个变量记作V₀。

(2) 从正态分布N(Q, θ Q)中生成一个随机数, 四舍五入取整记为Q^*, Q^*为候选变量子集V^*中变量的数量。

(3) 若Q^*=Q, 则令V₀=V^*; 若Q^*> Q, 需要在当前变量子集V₀中添加变量, 记作V^*; 若Q^*< Q, 需要在当前变量子集V₀中删除变量, 记作V^*。保证V^*中变量个数为Q^*。

(4) 确定是否可以接收V^*, 使用V₀和V^*计算交叉验证的误分类错误概率, 分别记作Err和Err^*。如果Err≤ Err^*, 则接收V^*作为V₁; 否则以η · Err/Err^*接收V^*作为V₁。

(5) 使用V₁中的变量更新V₀, 重复步骤2— 步骤4, 直到完成N次循环。

(6) 计算每个变量的选择概率: N次迭代后, 总共可以得到N个变量子集。记第j个变量被选入这些N个变量子集的频数为N_j。因此, 每个变量的选择概率可以使用式(2)计算

$Pro b_{j} = \frac{N_{j}}{N}, j = 1, 2, \dots, p$ (2)

(7)根据概率选择全集V中变量作为特征输出。

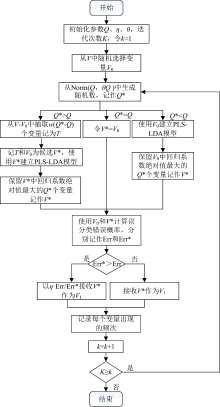
图2为RJFA具体算法的流程图。

	Figure Option View Download New Window
	图2 RJFA算法流程图Fig.2 Algorithm flowchart of RJFA

1.5 预测模型建立与评价

偏最小二乘回归以提取潜变量的形式降低数据维度, 从而避免了传统回归模型在多重共线性下的失效, 并在一定程度上捕捉非线性趋势, 提供稳定的预测结果。同时, PLS通过选择最能解释数据变异的主成分, 简化模型, 避免过拟合, 有效提升模型的泛化能力。与多元线性回归相比, PLS能更好地应对共线性问题; 相较于支持向量机等非线性模型, PLS在处理高维线性关系较强的木糖含量预测中效率更高且易于解释; 相比于主成分回归, PLS考虑了自变量与因变量的关系, 可以提供更高的预测精度。综合考虑, 选择PLS作为木糖含量的预测模型。

PLS通过在高维数据中提取一组潜变量, 同时考虑原来自变量空间的数据变化信息和自变量对因变量的解释作用, 完成一个稳健的回归模型的构建。设样本个数为n, 使用光谱仪扫描样本得到了m个波长数据点的近红外光谱数据, 则有n× m的自变量数据矩阵如式(3)。

$X = [x_{1}, x_{2}, \dots, x_{m}]$ (3)

式(3)中, x_i(i=1, 2, …, m)为n维列向量。矩阵X中每一行代表一个样本的近红外光谱数据, 每一列表示一个波长变量。模型输出为单变量时, 因变量矩阵Y可表示为y, 如式(4), 其中y_i(i=1, 2, …, n)为因变量实际值。

$Y = y = [y_{1}, y_{2}, \dots, y_{n}]^{T}$ (4)

自变量矩阵X和因变量矩阵Y与潜变量的关系分别用式(5)表示。式(5)为PLS的外部模型, 其中T=[t₁, t₂, …, t_a]∈ Rⁿ^×^a和U=[u₁, u₂, …, u_a]∈ Rⁿ^×^a分别为X和Y的得分矩阵, a为主元个数, t_i为自变量矩阵X的潜变量, u_i为因变量矩阵Y的潜变量, P=[p₁, p₂, …, p_a]∈ R^m^×^a和Q=[q₁, q₂, …, q_a]∈ R^r^×^a分别为各自的负荷矩阵。 E∈ Rⁿ^×^m和F∈ Rⁿ^×^r是残差矩阵。

$\{\begin{array}{l} X = T P^{T} + E = \sum_{i = 1}^{a} t_{i} {p^{T}}_{i} + E \\ Y = U Q^{T} + F = \sum_{i = 1}^{a} u_{i} {q^{T}}_{i} + F \end{array}$ (5)

由于矩阵T、 P、 U和Q的计算和主元个数a相关, 需要通过迭代式以列向量的形式逐个计算。自变量矩阵X与因变量矩阵Y之间的关系由式(6)表示。

$Y = X B_{PLS} + F$ (6)

式(6)中, B_PLS为权重向量w_i、负荷向量p_i和系数向量b_i的函数, 下面步骤为B_PLS的迭代求取过程。

(1) 令E₀=X和F₀=Y, 令i=1。

(2) 权值向量w_i由式(7)计算得到。 w_i为矩阵 ${E^{T}}_{i - 1}$ F_i_-1 ${F^{T}}_{i - 1}$ E_i_-1的最大特征值λ _i对应的特征向量w_i, i=1, 2, , …, a。

${E^{T}}_{i - 1} F_{i - 1} {F^{T}}_{i - 1} E_{i - 1} w_{i} = λ_{i} w_{i}$ (7)

(3)计算得分向量t_i, 公式如式(8)。

$t_{i} = E_{i - 1} w_{i}$ (8)

(4)使用式(9)计算E_i_-1和F_i_-1相应于t_i的负荷量p_i和b_i, 以及自变量矩阵X对应于得分向量t_i的权值向量 $w_{i}^{*}$ 。

$\{\begin{array}{l} {p^{T}}_{i} = {t^{T}}_{i} E_{i - 1} / ({t^{T}}_{i} t_{i}) \\ {b^{T}}_{i} = {t^{T}}_{i} F_{i - 1} / ({t^{T}}_{i} t_{i}) \\ w_{i}^{*} = (I - G_{1}) (I - G_{2}) \dots (I - G_{i - 1}) w_{i} \\ G_{i} = w_{i} {p^{T}}_{i} \end{array}$ (9)

(5)使用式(10)计算 ${E^{T}}_{i}$ F_i ${F^{T}}_{i}$ E_i。

$\{\begin{array}{l} {E^{T}}_{i} F_{i} {F^{T}}_{i} E_{i} = D^{T} ({E^{T}}_{i - 1} F_{i - 1} {F^{T}}_{i - 1} E_{i - 1}) D \\ D = I - w_{i} {p^{T}}_{i} \end{array}$ (10)

(6)令i=i+1, 重复步骤2— 步骤5, 计算新的w_i、 p_i、 b_i和t_i。

(7)使用式(11)计算PLS模型对于自变量矩阵X的输出。

$B_{PLS} = w_{1}^{*} {b^{T}}_{1} + w_{2}^{*} {b^{T}}_{2} + \dots + w_{a}^{*} {b^{T}}_{a}$ (11)

使用经过预处理和特征波长选择过后的近红外光谱数据进行PLS建模, 将光谱数据分为训练集和测试集, 用训练集建立模型, 测试集不参与建模过程。在模型的建立过程中要兼顾模型的泛化性能和预测性能, 选择合适的潜变量数量异常重要, 在模型预测性能和拟合优度变化不大的前提下, 尽可能降低模型潜变量个数, 提升模型泛化性能。

为检验回归模型的性能, 选用决定系数R²来评估模型的拟合优度与泛化能力, 使用预测均方根误差RMSEP和预测相对分析误差RPD来直观地评价模型的预测性能。 R²的计算公式如式(12), 其表示模型对数据变异的解释程度, R²取值范围在0到1之间, 数值越接近1, 表示模型对数据的拟合越好。使用训练集数据计算R²可以衡量模型在训练集数据上的拟合程度, 用于评估模型的拟合优度; 使用测试集数据计算R²可以衡量模型在训练集数据上的预测能力, 此时R²记作 $R_{p}^{2}$ , 是评估模型泛化性能的关键指标。 RMSEP 是用于评估模型预测精度的指标, 反映了模型预测值与实际值之间的偏差。 RMSEP 越小, 表示模型的预测精度越高, 其计算公式如式(13)。 RPD 是用于评估模型预测能力的指标, 通过比较数据的标准差和预测误差来衡量模型的相对性能, 其公式如式(14)。 RPD 越高, 表示模型的预测性能越好, 当RPD> 2.5时, 可以认为该模型具有良好的预测能力, 适用于定量分析^[15]。

$R^{2} = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{n} (y_{i} - {\bar{y}}_{i})^{2}}$ (12)

$RMSEP = \sqrt[]{\frac{\sum_{i = 1}^{n} ({\hat{y}}_{i} - y_{i})^{2}}{n}}$ (13)

$RPD = \sqrt[]{\frac{\sum_{i = 1}^{n} (y_{i} - {\bar{y}}_{i})^{2}}{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}}$ (14)

式(12)— 式(14)中, ${\hat{y}}_{i}$ 为因变量预测值, ${\bar{y}}_{i}$ 为因变量实际值的平均值。

2 结果与讨论

2.1 数据预处理

将采集得到的样品按4∶ 1分为训练集和测试集, 分别使用FD、 SG、 MA、 SNV等不同的方法对原始光谱数据进行预处理。不同的预处理方法会对预测模型的性能产生不同的影响, 使用处理过后的光谱数据建立PLS木糖预测模型, 通过比较评价指标确定最合适的预处理方法。使用不同预处理方法处理原始光谱数据后, 建立的预测模型的评价指标如表1所示。

表1 不同预处理方法的PLS建模结果 Table 1 Modeling results of PLS with different pretreatment methods

预处理	R²	RMSEP	RPD	$R_{p}^{2}$
Original	0.998 4	11.739 4	1.932 8	0.731 7
FD	0.998 9	11.502 0	2.041 6	0.742 5
MSC	0.999 8	12.270 3	1.910 7	0.706 9
SNV	0.998 7	12.193 9	1.912 4	0.710 6
SG	0.998 9	10.411 0	2.181 2	0.789 0
MA	0.989 1	13.035 0	1.744 6	0.669 3
CT	0.993 6	11.845 5	2.000 6	0.726 9
FD+SG	0.981 1	8.834 1	2.625 6	0.848 1

表1 不同预处理方法的PLS建模结果 Table 1 Modeling results of PLS with different pretreatment methods

由表1可知, 使用经不同预处理后的光谱数据建立的PLS模型的性能发生了不同的变化。 FD解决了原始光谱数据中的基线漂移问题, 模型的预测性能和拟合优度上升。由于样本为液体, 不存在颗粒大小、形状不均匀问题, 数据经过MSC、 SNV处理后, 信息略有损失, 模型性能有所下降。 MA处理虽然去除了噪声影响, 但是对光谱信息的边界点造成损失, 模型性能略微下滑, 改用SG方法处理噪声后, 模型性能略有上升。将FD方法和SG方法相组合, 同时去除基线漂移和噪声干扰, 模型的拟合优度和预测能力都得到进一步提升。

从表1中的模型评价指标可以看出, 使用FD与SG组合对原始光谱数据进行预处理后, $R_{p}^{2}$ 为0.848 1, RPD达到2.625 6, RMSEP也进一步缩小, 模型的性能最优。故选用FD与SG组合作为建模过程中的预处理方法。

2.2 波长特征选择结果

使用FD+SG方法组合对原始光谱数据进行预处理后, 建立的PLS模型的性能得到了提升, 但是由表1可以看到预处理后R²基本保持不变, 依旧接近1, 只进行预处理后光谱建立的模型存在过拟合现象, 光谱数据中依旧存在大量与木糖含量无关联的波长信息, 需要对预处理后的光谱数据进行特征选择, 期望提高预测模型的泛化能力, 降低预测误差和模型复杂度, 进一步提升模型性能。

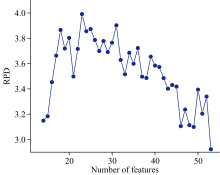
RJFA的关键参数为选择得到的特征数量, 该参数会对PLS模型的建模结果产生显著影响, 选择特征的数量过少可能会导致预测模型无法捕捉到数据的全部信息, 从而导致模型欠拟合; 选择过多则可能引入噪声和冗余特征, 导致模型过拟合, 降低模型的泛化性能。图3为不同特征数量下, 建立的PLS模型的评价指标变化趋势曲线。

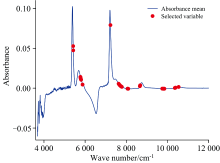
	Figure Option View Download New Window
	图3 RPD随特征数量变化的趋势曲线Fig.3 The trend curve of RPD with the number of features

从图3可知, 随选择得到的特征数量增加, RPD先上升后下降, 特征数量过小时, 模型对于光谱数据的解释性不足, 并不能较好的预测样本溶液中木糖含量的变化; 当特征数量过多, 模型欠拟合, 泛化性能下降, 使得其对新样本的预测能力不佳; 从图中变化趋势可以看出, 模型的预测性能在特征数量为20~30处最优。综合其他评价指标, 选择特征数量为25, 运行算法得到如图4所示的特征。从图中可以看出, RJFA从全谱中筛选出少量波长作为特征, 相比于全谱模型, 由于无关变量的减少, 模型的泛化性能将得到提高。

	Figure Option View Download New Window
	图4 RJFA特征波长选择结果Fig.4 Feature wavelength selection results of RJFA

2.3 模型预测结果对比

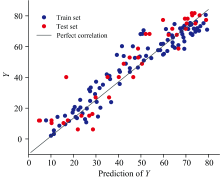
使用经过选择后得到的特征建立预测模型, 将训练集和测试集光谱数据输入模型, 得到预测值, 并与样本真实的木糖含量数据作对比, 结果如图5所示。图中横轴和纵轴分别表示样本预测值和实际值, 蓝色点和红色点代表训练集和测试集样本数据。

	Figure Option View Download New Window
	图5 RJFA-PLS模型预测效果Fig.5 Prediction effect of the RJFA-PLS model

从图5中可以看到, 蓝色点和红色点分布较为均匀, 且大部分靠近黑色实线, 表明模型在训练集和测试集上都具有较高的预测准确性。数据点离黑色实线的距离反映了预测误差, 离黑色实线越远误差越大。从图中可以看出, 虽然存在一些偏离较大的点, 但整体上误差较小。而且数据点的分布没有明显的差异, 表明模型在不同数据集上表现一致, 具有较好的泛化能力。

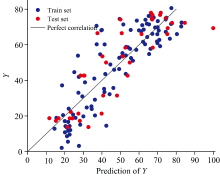
图6为PLS模型的预测效果图。先使用FD和SG方法处理原始光谱数据, 再运用主元分析对预处理后的光谱数据进行降维, 最后利用PLS算法建立预测模型, 得到的模型预测效果如图6所示。通过对比可以得出, 使用RJFA后进行特征波长选择, 建立的模型优于先进行主元分析再使用PLS算法建立的预测模型。 RJFA-PLS模型具有更高的预测准确性和更好的泛化能力, 而PLS模型在预测较高值时误差较大, 表现不如RJFA-PLS模型稳定。

	Figure Option View Download New Window
	图6 PLS模型预测效果Fig.6 Prediction effect of the PLS model

表2为PLS模型与RJFA-PLS模型的性能指标和潜变量个数对比。由表2可以看到, 相比于PLS模型, 使用RJFA进行特征波长特征选择后, 建立的预测模型的主元个数大幅度减少, 同时R²有所提升, 模型的拟合优度提升, 而RPD到达3.879 2, 同时RMSEP降低, 模型的预测性能提升。

表2 特征选择后的模型性能指标 Table 2 The model performance indices after feature extraction

预处理方法	特征选择	R²	RMSEP	RPD	$R_{p}^{2}$	潜变量个数
Original	无	0.998 4	11.739 4	1.932 8	0.731 7	58
Original	有	0.918 1	6.484 5	3.497 9	0.948 9	14
FD+SG	无	0.981 1	8.834 1	2.625 6	0.848 1	59
FD+SG	有	0.937 7	5.844 6	3.879 2	0.933 5	14

表2 特征选择后的模型性能指标 Table 2 The model performance indices after feature extraction

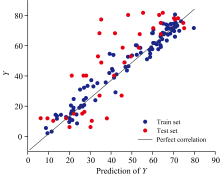
Lasso算法由于正则化项能使某些回归系数精确收缩为0, 从而实现变量的自动选择, 能够有效简化建模过程, 并通过正则化控制模型的复杂度, 防止过拟合。这一特性使得Lasso在处理只有一部分自变量与因变量相关的高维数据集时特别有用。 Lasso算法通过改变惩罚项系数λ 的大小来实现对预测系数的收缩, λ 范围在0到1之间。当λ =0时, 惩罚力度最小, 预测系数为最小二乘算法的原解, 当λ =1, 惩罚力度最大, 所有预测系数均为0。使用Lasso回归建模方法, 基于采集的近红外光谱数据, 选取λ =0.677 8为最优参数, 建立木糖含量的Lasso回归预测模型, 其预测效果如图7。

	Figure Option View Download New Window
	图7 Lasso模型预测效果Fig.7 Prediction effect of the Lasso model

从图7中可以看出, 散点分布相比于图6更为均匀, 但蓝点相对于红点明显更靠近黑色实线, 表明模型在训练集能够较好地预测样本木糖含量, 但在测试集木糖含量的预测表现不佳。虽然有一些数据点偏离黑色实线, 但整体上预测误差不算太大。

对比图5、图6和图7可以直观的看出, PLS模型的木糖含量预测值与实际值有较大偏差, 而Lasso算法虽然整体预测性能优于PLS算法, 但是在测试集数据的测定有一定的预测误差, 使用RJFA进行特征波长筛选后的木糖含量预测模型能实现更为精准的快速测定。表3为以上三个模型的性能指标对比, 从中可以看出, 使用RJFA进行波长特征筛选后, 模型的各项性能指标相较于PLS模型和Lasso模型的性能指标明显提高。

表3 模型的性能指标对比 Table 3 Comparison of model performance index

建模算法	R²	RMSEP	RPD	$R_{p}^{2}$
PLS	0.733 3	12.428 5	1.843 6	0.704 1
Lasso	0.684 5	15.696 1	1.447 1	0.520 4
RJFA-PLS	0.937 7	5.844 6	3.879 2	0.933 5

表3 模型的性能指标对比 Table 3 Comparison of model performance index

3 结论

从色谱分离工艺现场采集木糖样品, 结合木糖化学键和Beer-Lambert定律分析了使用光谱信息反映木糖含量的可行性。得到原始光谱数据后使用不同的预处理方法进行处理, 根据样品和预处理特性分析了模型评价指标变化的原因, 比较评价指标发现, 使用FD和SG组合建立的模型的性能最优。使用RJFA筛选得到25个特征波长, 再用加权累计后的特征建立木糖含量预测模型。相较于PLS模型, RJFA-PLS模型的潜变量个数大大减小, 数量从59个降低到14个, 模型的复杂度大大降低。 RJFA-PLS模型的各项评价指标均优于PLS模型, RMSEP降低了112.7%, R²、 RPD和 $R_{p}^{2}$ 分别提高了21.8%、 52.5%和24.6%。而Lasso算法在基于本数据集的木糖含量预测上表现并不理想。 RJFA-PLS模型能比Lasso模型和PLS模型实现更为精准的快速测定。

参考文献

文献列表

[1]	TANG Hui, CHENG Qiang, ZHANG Xue-rong(唐辉, 陈强, 张学荣). Journal of Food Safety & Quality(食品安全质量检测学报), 2020, 11(3): 955. [本文引用:1]
[2]	YANG Nan-lin, CHENG Yi-yu, QU Hai-bin(杨南林, 程翼宇, 瞿海斌). Acta Chimica Sinica(化学学报), 2003, 61(5): 742. [本文引用:1]
[3]	Lafuente V, Herrera L J, Pérez M D M, et al. Journal of the Science of Food and Agriculture, 2015, 95(10): 2033. [本文引用:1]
[4]	Mishra P, Roger J M, Rutledge D N, et al. Postharvest Biology and Technology, 2020, 170: 111326. [本文引用:1]
[5]	Dharmawan A, EviMasithoh R, Amanah H Z. Foods, 2023, 12(11): 2112. [本文引用:1]
[6]	Cruz-Tirado J P, Vieira M S D S, Correa O O V, et al. Journal of Food Composition and Analysis, 2024, 126: 105901. [本文引用:1]
[7]	ZHAO Jin-yi, CHEN Zheng-guang, YI Shu-juan(赵瑾熠, 陈争光, 衣淑娟). Chinese Journal of Analytical Chemistry(分析化学), 2024, 52(7): 1028. [本文引用:1]
[8]	XU Hong-fa, LIU Zheng-hui, ZHANG Hong-mei, et al(徐宏发, 刘正辉, 张红梅, 等). Journal of Zhejiang University (Agricalture and Life Sciences)[浙江大学学报(农业与生命科学版)], 2024, 50(3): 393. [本文引用:1]
[9]	JIA Wen-shen, LÜ Hao-lin, ZHANG Shang, et al(贾文珅, 吕浩林, 张上, 等). Smart Agriculture(智慧农业), 2024, 6(1): 89. [本文引用:1]
[10]	TANG Zi-ye, WEN Tao, DAI Xing-yong, et al(唐子叶, 文韬, 代兴勇, 等). Food & Machinery(食品与机械), 2024, 40(6): 124. [本文引用:1]
[11]	Felizardo P, Baptista P, Menezes J C, et al. Analytica Chimica Acta, 2007, 595(1): 107. [本文引用:1]
[12]	Kulcsár T, Sárossy G, Bereznai G, et al. Periodica Polytechnica Chemical Engineering, 2013, 57(1-2): 15. [本文引用:1]
[13]	YANG Zhen-fa, XIAO Hang, ZHANG Lei, et al(杨振发, 肖航, 张雷, 等). Chinese Journal of Analytical Chemistry(分析化学), 2020, 48(2): 275. [本文引用:1]
[14]	Nioka S, Chance B. NIR Spectroscopic Detection of Breast Cancer. Technology in Cancer Research & Treatment. 2005, 4(5): 497. [本文引用:1]
[15]	SUN Zhi-xing, ZHAO Zhong-gai, LIU Fei(孙志兴, 赵忠盖, 刘飞). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(3): 749. [本文引用:1]

2020

0.0

... 随后, Tang等将近红外光谱分析技术应用于流化床系统的控制, 利用探头对流化床一步制粒的全过程进行扫描采集光谱, 建立预测模型后, 使用该模型得到的温度和水分数据作为流化床干燥终点的判定条件, 为干燥终点的多变量控制提供了一种新思路^[1] ...

2003

0.0

... Yang等提出基于光纤近红外透射光谱的新分析方法, 对中药大孔吸附树脂纯化过程进行检测, 并成功地用于黄连生物碱提纯过程^[2] ...

2015

0.0

... 的MT硬度检测的可靠性^[3] ...

2020

0.0

... Mishra等采集苹果的光谱数据, 尝试使用动态正交化投影和域自适应两种方法对苹果的无损糖分检测模型进行校正, 两种尝试均取得成功^[4] ...

2023

0.0

... 近红外技术还被用于食品质量检测中, Dharmawan等完成了主成分分析(PAC)和机器学习算法的光谱技术开发工作, 并将该项技术用于检测咖啡豆来源^[5] ...

2024

0.0

... Cruz-Tirado等尝试使用近红外技术鉴别羊驼肉中掺入其他肉的行为, 取得良好效果^[6] ...

2024

0.0

... Zhao等使用近红外分析结合化学计量方法实现高粱单宁含量的快速检测^[7] ...

2024

0.0

... Xu等采集水稻节间样本, 构建水稻节间主要碳氮代谢组分模型, 为水稻栽培研究提供支撑^[8] ...

2024

0.0

... Jia等为了减少光谱仪购入成本, 将低分辨率光谱数据优化, 分辨霉变小麦, 并取得成功^[9] ...

2024

0.0

... Tang等采集柚子透射光谱数据, 在有限波长范围内建立近红外模型, 实现了柚子糖度的在线检测^[10] ...

2007

0.0

... Felizardo等使用NIR开发校准模型, 并在模型建立之前, 采用一阶Savitsky-Golay导数、二阶Savitsky-Golay导数和标准正态变换(SNV)等预处理方法对原始光谱数据进行预处理, 使模型的预测性能得到提升^[11] ...

2013

0.0

... Kulcsar等将近红外在线分析仪与偏最小二乘(PLS)相结合, 建立基于PLS的二维近红外光谱模型, 并将该模型应用于发动机缸的在线过程监控^[12] ...

2020

0.0

... Yang等使用漫反射近红外光谱仪扫描水泥生料, 采用X射线荧光光谱法标定参考值从而建立近红外光谱模型, 实现了水泥生料中氧化物含量的快速测定^[13] ...

2005

0.0

... Nioka等将近红外光谱技术应用于医学领域, 使用近红外窗口检测血液来定位癌症^[14] ...

2022

0.0

... 5时, 可以认为该模型具有良好的预测能力, 适用于定量分析^[15] ...