双光子跃迁(two-photon transition, TPT)通过吸收对向传播的两个光子, 消除了多普勒效应引入的谱线展宽效应, 获取的跃迁谱线线宽接近原子的自然线宽, 有利于高性能光频标的获得^{[1, 2]}。 基于双光子跃迁的光频标由于其频率稳定度高、 可集成化程度高等显著优势^{[3, 4, 5]}, 在基础物理^{[6, 7]}、 导航定位^{[5, 8]}、 激光通信^[9]、 引力波探测^[10]等领域具有重要的应用前景。

Nez等在1993年测得铷原子5S-5D的双光子跃迁谱线, 发现双光子跃迁谱线具有较高的信噪比, 利用该方法实现的光频标频率稳定度为7× 10^-12τ ^-1/2(1~100 s), 频率不确定度为5 kHz^[11]。 Martin等详细分析了影响光频标短期和长期稳定度的各项因素, 频率稳定度提升至4× 10^-13τ ^-1/2(1~10 000 s)^[12]。 Luiten等使用780和776 nm的双色激光作为光源, 实现了铷原子双光子跃迁光频标, 频率稳定度为1.5× 10^-13τ ^-1/2(1~8 000 s), 质量为17 kg, 体积为25 L^{[13, 14]}。 Lemke等研究了“ 漏氦” 效应对光频标长期稳定度的影响, 将物理部分放置到真空环境下进行了长达65 d的频率测量, 光频标的天稳定度提升至5× 10^-15[15]。 美国还计划在2024年底将小型化铷原子光钟搭载到NTS-3技术卫星上进行飞行验证^[16]。 在国内, 中国科学院武汉精测院^[17]、 中国科学院上海光机所^[18]、 北京大学^{[9, 19]}、 兰州空间技术物理研究所^[20]、 山西大学^[21]等多家单位也相继开展了⁸⁷Rb原子双光子跃迁光频标的研究工作并取得重要进展。

双光子跃迁光频标的频率稳定度可由式(1)表示^[22]

σ=1k1Q1SNR=1k1ν0/Δν1SNR(1)

式(1)中, k为与谱线线型相关的常数, Q= ν0Δν被称为频标的品质因子, ν ₀是原子跃迁频率, Δ ν 为原子跃迁谱线的线宽, SNR是谱线的信噪比。 由式(1)可以得出, 在原子跃迁谱线线宽一定时, 增加谱线信噪比是提高双光子跃迁光频标频率稳定度的有效途径。 然而, 光频标谱线信噪比在实验中容易受到激光光强、 原子数密度等多种物理参数的影响, 使谱线信噪比受到不同程度的恶化, 并最终影响光频标的频率稳定度^{[23, 24, 25, 26]}。

笔者以1 556 nm通信波段的种子激光作为光源, 通过激光倍频的方式产生778 nm钟激光, 实现了⁸⁷Rb原子双光子跃迁谱线的获取。 从激光功率、 原子数密度、 光电倍增管增益等关键参数出发, 系统研究了双光子光频标谱线信噪比的影响因素, 获得的双光子跃迁谱线信噪比最高达到2 600, 为未来高性能小型光频标的获得奠定了重要技术基础。

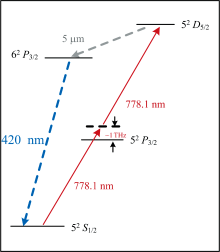
图1是铷原子双光子跃迁的能级图, 处于基态5²S_1/2的原子吸收两个反方向传播的778.1 nm的光子后发生双光子跃迁并被激发至5²D_5/2态, 之后原子将沿5²D_5/2→ 6²P_3/2→ 5²S_1/2的路径自发辐射, 并辐射420 nm的荧光, 对该荧光收集就可以得到双光子跃迁谱线的信息。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 双光子跃迁原理图Fig.1 Schematic diagram of two-photon transition

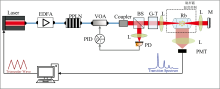
本实验利用如图2所示的装置来激发⁸⁷Rb原子发生双光子跃迁。 线宽为2 kHz的1 556 nm窄线宽激光器(Laser)出射的种子激光通过掺饵光纤放大器(EDFA)将激光功率放大至1.5 W。 光纤波导倍频模块(PPLN)将1 556 nm激光倍频至实验所需的778 nm钟激光, 倍频效率> 10%。 光纤连接的可调功率衰减器(VOA)实现对激光功率的稳定控制, 最大输出功率达到60 mW。 经激光准直器(Coupler)出射的激光被激光分束器(BS)分成两部分, 约10%的反射光用于对激光功率的监测, 并反馈至VOA实现对激光功率的稳定控制。 剩余90%的激光经透镜聚焦后入射到铷原子气室中, 后由第二个透镜准直, 焦点位置处于原子气室中心。 准直后的激光经光路末端的平面反射镜进行反射, 调节反射镜角度使得入射光和反射光重合。

铷原子气室放置在两层磁屏蔽中来减小背景磁场变化对频标稳定性的影响。 磁屏蔽外侧缠绕加热材料将气室温度维持在100 ℃左右, 以提高荧光信号的强度。 磁屏蔽侧壁中心位置开设圆孔, 原子发出的420 nm荧光通过圆孔向外辐射, 经透镜聚焦和420 nm带通滤光片滤除背景光后被光电倍增管(PMT)收集。 利用工控机产生一个峰值为1V的三角波信号, 该信号加载到激光器PZT调制端口实现对激光频率1 GHz范围的扫描, PMT输出的信号再经工控机模拟电压采集端口实现信号的采集和分析。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 双光子跃迁光频标装置原理图 L: 透镜; PD: 光电管; BS: 激光分束器; G-T: 格兰-泰勒棱镜; M: 反射镜; PID: 比例-积分-微分电路Fig.2 Experimental schematic diagram of optical frequency standard based on two-photon transition L: Lens; PD: Photodiode; BS: Beam splitter; G-T: Glan-taylor prism; M: Mirror; PID: PID servo circuits

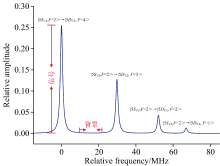
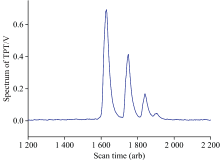
⁸⁷Rb原子双光子跃迁谱线示意图如图3所示, 图中有4个双光子跃迁共振峰, 从左到右分别对应⁸⁷Rb原子|5S_1/2, F=2> → |5D_5/2, F=4, 3, 2, 1> 跃迁, 本文中分析的信噪比均为|5S_1/2, F=2> → |5D_5/2, F=4> 跃迁谱线的信噪比。 文中的信噪比计算方法为信号振幅与背景噪声的比值, 其中信号振幅通过对图3中的“ 信号” 部分做洛伦兹拟合得到, 背景噪声通过计算图3中“ 背景” 部分的标准差得到。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 87Rb原子双光子跃迁谱线示意图Fig.3 Transition spectral lines diagram of 87Rb based on two-photon transition

2.1 激光光强

原子在对向传播的两束激光作用下发生双光子跃迁, 跃迁概率Γ _if由式(2)表示^[27]

Γif∝γifI1I2[ωif-ω1-ω2-v(k1+k2)]2+(γif/2)2· ∑kDike1Dkfe2ωki-ω1-vk1+Dike2Dkfe1ωki-ω2-vk22(2)

式(2)中, I₁和I₂为两束激光的光强, γ _if为谱线的均匀展宽宽度, ω _ik和D_ik分别为能级i和能级f之间的跃迁频率和跃迁矩阵元, e₁和e₂为偏振单位矢量。 从式(2)可以看出, 双光子跃迁的概率与激发原子的两束激光光强的乘积成正比。 激光光强越大, 双光子跃迁的概率越大, 原子辐射的420 nm荧光就越强, 在探测噪声一定时获得的跃迁谱线的信噪比也就越高。

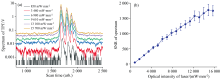
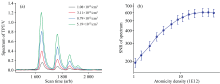
为了定量分析双光子跃迁荧光谱线信噪比和激光光强的关系, 将聚焦后的光斑尺寸固定, 通过改变钟激光的功率来实现对激光光强的调制。 光斑尺寸通过光束轮廓仪来进行测量, 直径为70 μm。 钟激光功率的变化是通过改变VOA的控制电压来实现的, 并通过伺服环路对激光功率进行锁定。 将原子数密度和PMT增益分别设置为7.5× 10¹² cm^-3和1.1× 10⁵, 在不同钟激光光强下采集双光子跃迁谱线, 结果如图4(a) 所示。 随着激光光强的增加, 信号的幅值有了明显的增加, 但PMT输出的噪声本底和大小也相应增加。 对每条谱线进行分析, 即可得到谱线信噪比随激光光强的变化关系, 结果如图4(b)所示。 在850~15 700 mW· mm^-2的激光功率范围内, 谱线的信噪比随激光光强的增加呈线性关系, 最大值达到1 800。 受限于实验系统中激光光强的限制, 未能对> 15 700 mW· mm^-2时谱线的信噪比进行分析, 但从图4(b) 中谱线信噪比随激光光强的变化趋势来看, 谱线信噪比将随着钟激光光强的增加而继续提升。 考虑到激光光强增大对谱线展宽的影响, 将钟激光的光强减小至5 000 mW· mm^-2, 谱线的信噪比为600, 是最大值的1/3。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 激光光强对跃迁谱线信噪比的影响 (a): 不同激光光强下的荧光信号; (b): 信噪比随激光光强的变化关系Fig.4 The relationship between laser intensity and SNR of transition spectral lines (a): Fluorescence signals under different laser intensities; (b): Relationship between SNR and laser intensity

2.2 原子数密度

为了提高原子跃迁效率, 在原子气室前后放置两个凸透镜, 将钟激光聚焦至70 μm左右, 仅处于该空间范围内的原子才能参与双光子跃迁。 因此, 增加作用区内的有效原子数目能够直接提升荧光信号的大小, 进而提升跃迁谱线的信噪比。 原子气室中的⁸⁷Rb原子数密度可通过式(3)表示,

n=1T1021.866+A-B/T(3)

式(3)中, T为原子气室的温度, A和B为无量纲常数, 在铷原子系统中这两个值分别为4.312和4 040^[28]。 从式(3)可以看出, 原子数密度值只与气室的温度相关, 通过增加气室的温度就可以增加作用区内原子的数目, 从而有效提升谱线的信噪比。

设置钟激光光强为5 000 mW· mm^-2, 图5(a)所示为不同原子数密度下获取的部分原子跃迁谱线, 气室温度从75 ℃增加至137 ℃, 原子数密度对应从1.1× 10¹² cm^-3增加至5.2× 10¹³ cm^-3, 谱线峰值随着原子数密度的增加而显著增大。 图5(b)为谱线信噪比随原子数密度的变化关系, 可以看到原子数密度在1.0× 10¹²~1.5× 10¹³ cm^-3区间时, 谱线的信噪比随着原子数密度的增加而提升, 当原子数密度高于1.5× 10¹³ cm^-3后, 谱线的信噪比约为600并不再明显变化。 考虑到国际计量局(BIPM)对Rb原子双光子光频标跃迁频率推荐值对应的温度不超过100 ℃^[29], 将本系统的原子数密度设定为6.4× 10¹² cm^-3左右, 此时谱线信噪比为450, 是最大值的3/4。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 原子数密度对跃迁谱线信噪比的影响 (a): 不同原子数密度下的荧光信号; (b): 信噪比随原子数密度的变化关系Fig.5 The relationship between atomicity density and SNR of transition spectral lines (a): Fluorescence signals under different atomicity densities; (b): Relationship between SNR and atomicity density

2.3 PMT增益

利用778 nm的单色激光激发双光子跃迁, 原子的跃迁效率低导致荧光信号非常弱^[5]。 PMT作为灵敏度最高的光电探测器之一, 被用到双光子跃迁实验中微弱荧光信号的获取。 虽然实验中选用的PMT暗电流已经低至< 10 nA, 但是相对微弱的荧光信号, 依然会对谱线的信噪比造成影响。 在激光光强一定时, 适当增加PMT的增益将有利于谱线信噪比的提升。

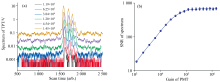
图6(a)所示为钟激光光强固定为5 000 mW· mm^-2、 原子数密度为6.4× 10¹² cm^-3时, 不同PMT增益下获取的双光子跃迁谱线, 随着PMT增益的增加, 谱线的信噪比有了明显的提升。 图6(b)为谱线信噪比随PMT增益的变化曲线, 在PMT增益小于1.2× 10⁵时, 谱线信噪比随PMT增益的增加而增加, PMT增益大于1.2× 10⁵后, 谱线信噪比达到一个平坦区, 不再随着PMT增益的增加而发生明显的变化。 因此, 本系统中将PMT增益设置为1.2× 10⁵, 谱线信噪比为650。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 PMT增益对跃迁谱线信噪比的影响 (a): 不同PMT增益下的荧光信号; (b): 信噪比随PMT增益的变化关系Fig.6 The relationship between gain of PMT and SNR of transition spectral lines (a): Fluorescence signals under different PMT gains; (b): Relationship between SNR and PMT gain

2.4 优化之后的荧光谱线

考虑到双光子跃迁光频标的谱线线宽以及BIPM推荐的Rb原子双光子光频标跃迁频率的实现温度, 将双光子光频标系统的参数设置为: 激光光强为5 000 mW· mm^-2、 原子数密度为6.4× 10¹² cm^-3(对应原子气室温度约100 ℃)、 PMT增益为1.2× 10⁵, 获取的原子跃迁谱线如图7所示, 谱线信噪比达到650。 根据各参数调制实验的结果可知, 本系统获取的双光子光频标跃迁谱线信噪比最高能够达到2 600, 较文献[18]中报道的结果高近一个量级。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 优化之后的双光子跃迁谱线Fig.7 The optimized two-photon transition spectral lines

基于双光子跃迁的小型化光频标具有频率稳定度高、 可集成化程度高等优势, 未来有望成为星载原子钟的有力候选。 谱线信噪比是影响光频标短期稳定度的重要参数, 高信噪比光频标跃迁谱线是高性能光频标实现的前提。 本文从激光光强、 原子数密度、 光电倍增管增益三个方面, 对基于双光子跃迁的光频标跃迁谱线信噪比的影响因素进行了实验分析。 激光光强在850~15 700 mW· mm^-2范围内时, 光频标谱线的信噪比随激光功率的增加而线性增加; 原子数密度低于1.5× 10¹³ cm^-3时, 谱线的信噪比随着原子数密度的增加而增加, 当原子数密度高于1.5× 10¹³ cm^-3后, 谱线的信噪比不再发生明显变化; 光电倍增管增益对光频标谱线的信噪比也有影响, 当PMT增益小于1.2× 10⁵时, 谱线信噪比随PMT增益的增加而增加, 大于1.2× 10⁵后, 谱线信噪比不再随着PMT增益的增加而变化。 本系统获得的双光子跃迁光频标谱线信噪比最高能够达到2 600, 考虑双光子跃迁谱线的线宽为1 MHz, 光频标短期频率稳定度预期将达到~3× 10^-13τ ^-1/2。 本文通过对铷原子双光子光频标谱线信噪比的影响因素进行研究, 获得了高信噪比原子跃迁谱线, 对未来高性能集成化双光子光频标的研制具有重要意义。