作者简介: 张亚飞, 1995年生,兰州空间技术物理研究所工程师 e-mail: 2515617220@qq.com
随着传统计量标准的量子化转变, 基于光学方法的量子真空计量技术得到发展。 结合基于光学干涉法的量子真空计量技术与空间外差干涉光谱技术, 提出了一种新的利用折射率测量气体压力的方法。 将空间外差干涉仪两臂通路设置为可抽放气的封闭腔室, 腔室内气体压力变化时, 气体的折射率随之改变, 折射率变化改变了光线在两臂的传播光程, 造成干涉条纹空间频率、 相位等特征的变化, 可从中反演气体压力。 首先基于折射率对光栅衍射角的影响分析, 计算光程差得到了含折射率的空间外差干涉条纹理论表达式, 通过理论分析可得, 折射率变化带来干涉仪Littrow波长参数的漂移, 以此造成条纹空间频率和相位的变化; 然后基于该理论表达式进行了数值仿真, 当气压从0 ATM变化至1 ATM时, 采样条纹周期和相位的最大变化量分别为6.21周期和19.50 rad; 又以相同参数建立光学模型进行了光线追迹仿真, 并对仿真干涉图以相同的傅里叶方法反演, 反演结果中条纹周期数和相位在相同气压变化下的变化与数值仿真非常接近, 相差仅为5.6×10-3周期和0.014 8 rad, 验证了本文提出的含折射率影响的空间外差干涉条纹的理论表达, 说明了基于此理论进行折射率反演进而计算气体压力的可行性; 最后讨论了改变Littrow波长和增加光程差扫描范围两种进一步提升相位响应灵敏度的方法, 并进行了改变光栅衍射级次和增加光程差偏置量的仿真, 仿真中相比一级衍射改变级次可以得到衍射级次倍的提升, 相比对称结构增加1 mm的偏置量也提升了27.65%的相位响应, 证明了经过优化设计后可以进一步提升利用空间外差干涉仪进行气体压力测量的可行性。
With the quantization transformation of traditional metrology standards, quantum vacuum metrology technology based on optical methods has been developed. Combining the quantum vacuum metrology technology based on optical interference and spatial heterodyne interference spectroscopy, this paper proposes a new method for measuring gas pressure using refractive index. The two-arm passages of the spatial heterodyne interferometer are set as closed chambers that can be evacuated and de-aerated. When the gas pressure in the chamber changes, the refractive index of the gas changes accordingly. The change in refractive index changes the propagation path of light in the two arms, causing changes in the spatial frequency, phase and other characteristics of the interference fringes, from which the gas pressure can be inverted. In this paper, based on the analysis of the influence of refractive index on the grating diffraction angle, the optical path difference is calculated to obtain the theoretical expression of spatial heterodyne interference fringes containing refractive index. Through theoretical analysis, it is obvious that the change in refractive index brings about the drift of the Littrow wavelength of the interferometer, thereby causing the change of the spatial frequency and phase of the fringes. Then, numerical simulation is carried out based on the theoretical expression. When the air pressure changes from 0 ATM to 1 ATM, the maximum changes of the sampling fringe period and phase are 6.21 periods and 19.50 rad, respectively. An optical model is established with the same parameters for ray tracing simulation, and the simulated interference pattern is inverted with the same Fourier method. The changes of the fringe period and phase under the same air pressure change in the inversion result are very close to the numerical simulation, with a difference of only 5.6×10-3 periods and 0.014 8 rad, which verifies the theoretical expression of spatial heterodyne interference fringes with refractive index effect in this paper, and illustrates the feasibility of refractive index inversion and gas pressure calculation based on this theory. Finally, two methods of changing Littrow wavelength and increasing optical path difference scanning range to further improve phase response sensitivity are discussed, and simulations of changing grating diffraction order and increasing optical path difference offset are carried out. In the simulation, compared with the first-order diffraction, changing the order can increase the diffraction order by times, and increasing the offset of 1 mm compared with the symmetrical structure also improves the phase response by 27.65%, which proves that the feasibility of using spatial heterodyne interferometer for gas pressure measurement can be further improved after optimized design.
真空测试计量是一门实现真空量值准确、 可靠传递以及真空下多参数综合测试的技术基础及应用科学, 在航空航天、 半导体以及各类精密仪器和高端装备制造等领域发挥着重要的基础支撑作用[1, 2]。 随着国际单位制中各种传统实物计量标准的量子化转变, 为了实现量子化真空计量标准, 基于光学方法的新型真空计量技术也得到进一步发展, 目前主要基于光学干涉、 光谱吸收和冷原子三种技术原理[3, 4]。
光学干涉法进行真空计量的主要原理是激光穿过气体介质时折射率引起光程变化, 对折射率进行测量进而反演气体密度和压力。 美国国家标准与技术研究院NIST率先进行了利用干涉法建立真空压力标准的设想, 并在2015年研制了基于双F-P光学干涉腔结构的真空测量装置, 利用折射率造成的干涉腔的谐振频率变化反演气体压力, 对比测得宏观折射率和用ab-initio算法得到的分子折射率, 建立了真空计量标准, 其后又开发了基于可变长度F-P谐振腔的折射率测量装置VLOC和三腔结构单面干涉折射率测量装置MIRE。 除了NIST之外, 瑞典Umeå 大学、 日本AIST、 中国的计量科学研究院、 东北大学、 兰州空间技术物理研究所等机构也建立了基于F-P光学干涉腔的真空测量装置[5, 6, 7, 8, 9]。
除了F-P光学干涉腔结构外, 也有其他的干涉结构用于真空计量研究。 2014年, 意大利国家计量院研制了一台动态真空校准装置, 装置主体部分为一台高灵敏度、 零臂差的Michelson干涉仪, 由高速摄影机记录两臂信号形成的Lissajous图形, 反演得到折射率和真空压力[9, 10]。
空间外差光谱仪(spatial heterodyne spectrometer, SHS)是近些年来新兴的一种干涉光谱技术, 其结构与Michelson干涉仪相似, 只是干涉仪两臂末端替换为两块参数相同的倾斜固定的光栅; 具有结构简单、 加工装调工艺要求较低、 光谱分辨率高以及光通量大的优势, 非常适合应用于精细光谱探测领域[11, 12]。
为了探索基于空间外差干涉技术实现气体折射率测量进而反演真空压力的可行性, 通过光程差分析得到了含有气体折射率影响的SHS干涉条纹理论表达; 分析折射率变化对条纹相位、 空间频率等特征的影响, 设计了条纹反演得到折射率及真空压力的数据反演流程和方法, 并通过光线追迹进行仿真, 讨论了系统进行真空压力计量的性能, 以及干涉仪热稳定等因素对探测性能的影响。 与基于Michelson和F-P干涉仪的气体压力测量方法相比, SHS虽然由于光谱分辨率的劣势在测量精度上有所不及, 但SHS结构简单、 加工装配工艺要求低因此在成本上会更有优势, 而且具备多谱线同时测量的能力, 为仪器实现实时标定、 基于成分探测的分压力测量提供了可能性。
介质的折射率可以视为光在真空中的传播速率与介质中传播速率的比值, 而光作为一种电磁波可以用麦克斯韦方程来描述, 因此折射率n可以用介质的相对介质常数ε r和相对磁导率μ r表示为: n2=ε rμ r, 则折射率n和气体密度ρ (单位为mol· cm-3)之间的关系可以表示为[13, 14]
式(1)中, 摩尔极化率Aε =4π NAα /3, 摩尔磁化率Aμ =4π NAχ /3, NA为阿伏伽德罗常数, α 为原子极化率, χ 为原子磁化率, Bε 为第二介电维里系数, 是温度的函数。
通过维里状态方程, 气体密度ρ 和气体压力P可以建立如式(2)联系[13, 14]
式(2)中, R为气体常数, T为温度, B(T)是第二维里系数, 代表最低阶偏离理想气体的行为, 它只是分子对间相互作用的函数。 如此结合等式(1)和式(2), 可以得到气体压力与气体折射率之间的关系如式(3)[13, 14]
式(3)中, kB为玻尔兹曼常数。
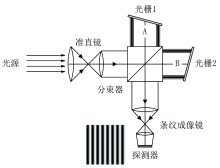
SHS基于Michelson干涉原理发展而来, 其基本结构和工作原理如图1所示, 入射光经过准直镜的准直, 进入干涉仪被分束器分为两束光, 分别到达光栅, 经过光栅的衍射作用返回分束器, 在空间中相遇形成Fizeau干涉条纹[11, 12]。 SHS中, 光栅以Littrow角θ L倾斜固定, 根据光栅衍射的波长选择作用, 只有Littrow波长的光沿着光轴入射到光栅上可以原路返回, 其他波长的光返回的方向与光轴的夹角与波长与Littrow波长的波长差相关。 这样不同波长的光入射到SHS, 根据与Littrow波长的波长差形成不同空间频率的干涉条纹叠加, 类似余弦级数, 因此SHS可以通过傅里叶变换方便地得到入射光谱信息。
SHS中干涉像面上, 光程差取决于出射波前的倾角γ , 不考虑元件间介质的折射率影响, 认为折射率为1, Littrow波数σ L的光与一般波数σ 的光分别入射到光栅时, 可根据光栅方程得到如式(4)关系[15]
式(4)中, dgrating是光栅的光栅常数。 根据等式(4)可以计算得到光线出射角γ , 进而计算光程差, 通过光程差得到SHS的干涉条纹表达式[15]
式(5)中, I0为入射强度, x为干涉方向坐标。
考虑元件间介质折射率的影响, 则等式(4)根据光栅方程可改写为
式(6)中, σ n, L是折射率n对应的Littrow波数, 根据等式(6), SHS的干涉条纹理论表达式可以改写为
从等式(7)中可以看出, 在SHS干涉中引入折射率的影响主要是造成干涉仪Littrow波数的漂移, 改变后的Littrow波数为σ L/n。 这样设计如图1所示的测量结构, 分束器与干涉仪两臂光栅之间的结构设计为密封的A、 B两个腔室, A、 B两腔室连通以保持气体成分压力相同, 则当腔室内的气体压力变化时, 气体折射率变化, 造成SHS干涉仪的Littrow波数变化, 干涉条纹随之改变。 如此便可通过干涉图的反演计算折射率, 进而得到腔室内的真空压力。
当SHS干涉仪两臂腔室内的气体压力变化时, 腔内环境折射率的变化造成光栅表面光线衍射出射角的变化, SHS干涉仪系统的Littrow波长随之发生漂移。 为了验证利用Littrow波长漂移造成的条纹变化进行气体压力测量的可行性, 分别基于数值方法和光线追迹对气体压力对SHS干涉条纹频率与相位的影响进行仿真。
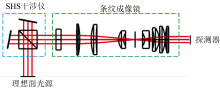
首先进行了基于空气折射率变化的SHS干涉系统数值仿真, 仿真所用SHS干涉系统参数如表1所示。 干涉条纹数据根据等式(7)计算得到, 再从中反演条纹周期、 相位等信息进行对比。 反演方法和过程如图2所示, 对去基线后的条纹进行傅里叶变换得到频谱, 从频谱中提取特征峰进行傅里叶逆变换得到复干涉图, 通过求解复干涉图的幅角再进行相位展开补齐即可得到相位分布。 为了减小变换过程中窗口截断效应带来的相位畸变误差, 对相位进行了线性拟合处理。
| 表1 仿真SHS干涉系统参数 Table 1 Parameters of SHS simulating system |
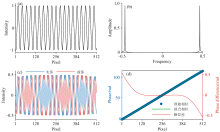 | 图2 基于傅里叶变换的SHS数据反演方法示意Fig.2 Schematic diagram of SHS data inversion method based on Fourier transform |
仿真过程中, 空气折射率根据Kohlrausch等在Praktische Physik中提出的计算方法得到[16]
式(8)中, P为大气压强, 单位为ATM(标准大气压), λ 为波长, 单位μ m, T为温度, 单位为℃。
图3(a)、 (b)、 (c)分别展示了温度为20 ℃, 气压变化时, 干涉仪Littrow波长、 采样范围内的条纹数以及条纹相位的变化, 条纹数通过相位区间除以2π 计算得到。 可以看出当压强从0 ATM变化到1 ATM时, 三者都发生显著变化, Littrow波长变化量为0.17 nm, 条纹数变化为6.21。 相位的变化与像元位置相关, 探测器边缘处变化大、 中心位置小, 这是因为仿真干涉仪系统两臂对称没有额外光程差, 当Littrow波长漂移变化时, 条纹的变化关于零光程差位置也就是探测器中心对称。 在1像元处, 相位的变化量为19.50 rad。
为了进一步验证SHS干涉仪系统对环境气压变化的响应。 依托如图4所示的光学模型, 进行了光线追迹仿真, 模型中利用理想面光源照亮SHS干涉仪, 经条纹成像镜成像至探测器。 条纹成像镜可以在干涉定域面位置发生变化的情况下依然保持对条纹的清晰成像, 条纹成像镜的画质已达到衍射极限, 畸变与成像放大率随环境气压的变化经仿真可以忽略不计。 建立模型所用参数与表1一致, 可以与理论计算结果直接进行对比。
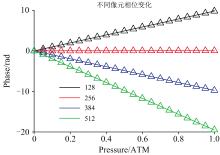
图5(a)、 (b)展示了光线追迹所得条纹的条纹周期与1像元处相位随环境气压的变化, 以及与根据等式(7)计算的对比, 两组干涉条纹经过相同的傅里叶反演得到周期数与相位。 从图中可以看出, 仿真与计算的结果非常接近, 条纹数和相位的最大差分别为5.6× 10-3周期和0.014 8 rad。 它们的差异整体呈现出随机变化的特征, 条纹数的差异有略微上涨的趋势, 而相位则是略微下降的趋势, 这主要是因为条纹成像镜的成像放大率没有得到足够精确的测量, 计算所用成像放大率与光学模型的真实放大率之间存在误差。 图6展示了其他不同像元位置处相位随压强的相对变化, 可以看出仿真与计算结果在趋势和数值上都非常接近。
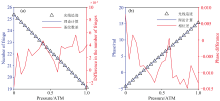 | 图5 光线追迹仿真中条纹数和相位随气压的变化, 以及与理论计算结果的对比Fig.5 The variations of fringe number and phase with air pressure in ray tracing simulation and comparison with theoretical calculation results |
通过光线追迹仿真, 验证了等式(7)中SHS干涉条纹关于气体折射率的响应。 条纹数和相位在气体压强从0 ATM变化至1 ATM时都发生了显著的变化, 边缘处相位的变化可以达到接近20 rad, 证明了从中反演环境折射率进而计算气体压强的可行性。
根据之前的理论和仿真, SHS的条纹相位与环境气体压强之间是线性相关的关系, 而在仿真中当压强从0 ATM变化至1 ATM时, 相位的最大变化19.50 rad, 可以认为相位对压强的响应约为0.19 mrad· Pa-1, 该系统要达到1 Pa内的测量精度, 需要优于0.19 mrad的相位灵敏度, 这对SHS系统来说是一个挑战。 在本文的SHS气体压力测量系统中, 可以通过改变Littrow波长或者增加光程差扫描范围的方法提升灵敏度。
根据等式(6)和式(7), 环境气体折射率为n时, SHS干涉仪的Littrow波数为σ L/n, 其中σ L是真空环境中的Littrow波数。 当折射率变化Δ n时, Littrow波数的变化为
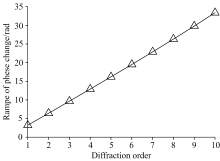
式(9)中, Δ n由气体压强的变化决定, 因此σ L越大, Littrow波数的变化Δ σ L越大, 干涉相位的变化也越大。 Littrow波数可以通过改变光栅的倾斜角或者衍射级次实现, 图7展示了表1中系统利用光栅不同衍射级次, 当气压从0 ATM变化至1 ATM时, 像元1处相位变化范围的变化。 为了避免条纹空间频率差异在反演过程中带来的计算误差, 每组仿真所用入射波长分别设置使得条纹数相同。 可以看出衍射级次的改变能显著影响相位对气压的响应, 衍射级次越高, 相位变化越大, 意味着相位对压强的变化也更加敏感, m级衍射下的相位灵敏度约为1级的m倍。 根据2.2小节中的理论, 衍射级次对相位的影响是线性的。
光程差扫描范围的增加有两种途径, 一种是增大光栅有效宽度, 这会改变整个系统的口径大小; 还有另外一种是在干涉仪两臂增加非对称偏置。 在SHS干涉仪中, 两臂光路完全对称, 零光程差位置在干涉图中心位置, 光程差、 相位分布左右对称, 当气压变化时, 越往干涉图边缘处, 相位变化越大, 干涉图最左与最右像元处的相位变化相同, 图3(c)也验证了这一点。 当改变干涉仪其中一臂的长度, 零光程差位置在干涉图中横移, 这增加了其中一端的光程差采样范围, 当气压变化时, 相位的变化也更大。 非对称SHS的干涉条纹理论表达式为[15]
式(10)中, Δ d为干涉仪两臂的非对称偏置量。 结合等式(7), 再考虑折射率n对光程的影响, 等式(10)可以改写为
对于常用可见光波长来说, 波数σ 数值较大, 因此初始相位项2σ nΔ d会对其余两项的微小变化敏感。 当折射率n随着气压变化, 空间频率的变化叠加初始相位的变化, 系统的相位响应更灵敏。 图8展示了利用表1中的系统参数仿真, 不同偏置量下, 当气压从0 ATM变化至1 ATM时, 干涉图中最大相位变化量的变化, 增加1 mm的光程差偏置量后, 相位灵敏度提升了27.65%。
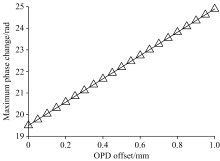 | 图8 不同偏置量下干涉图的最大相位变化Fig.8 Maximum phase variation range of the interference pattern under different OPD offset |
通过以上的分析和仿真, 可以看出干涉仪的光程偏置和衍射级次对相位响应有显著影响, 在这两方面进行合理的设计优化后, 相位对气压的响应灵敏度可以得到显著提升, 有助于提高利用SHS系统进行气体压力测量的可行性和实用性。 但需注意的是, 衍射级次的增大会降低衍射光强度, 非对称偏置量的增加也会降低干涉条纹的调制度, 因此在实际优化设计中需要进行取舍选择最优大小。 从以上的理论和仿真中也可以看出, SHS系统对压强的响应是线性的, SHS还具有多谱线同时测量的能力, 会在测量和标定中带来诸多便利, 将会成为一个重要优势。
结合SHS与基于光学干涉法的量子真空计量, 提出了一种利用空间外差干涉仪测量气体折射率进而反演其压力的方法。 首先通过对光栅衍射关系的分析, 计算得到含环境折射率影响的SHS干涉条纹理论表达式, 根据理论分析SHS中折射率的变化造成Littrow波长的漂移改变条纹的空间频率和相位。 然后进行了数值仿真, 其中当气压从0 ATM变化至1 ATM时, 采样条纹数和相位的最大变化量分别为6.21个周期和19.50 rad, 之后的光学追迹仿真对比中, 条纹经过相同的反演后, 所得条纹数和相位的变化量非常接近, 差异仅为5.6× 10-3周期和0.014 8 rad, 验证了SHS对折射率的测量理论以及基于折射率进行气体压力测量的可行性。 该仿真系统中相位对气压的响应约为0.19 mrad· Pa-1。 讨论了两种提高相位响应灵敏度的途径并进行仿真, 第一种为改变光栅衍射级次, 每个衍射级次下的相位响应约为一级衍射下的衍射级次倍; 第二种为在干涉仪两臂间增加光程差偏置, 通过零光程差位置的偏移增大光程差采样范围, 仿真中当增加1 mm的偏置量后, 相位响应提升了27.65%。 结合这两种方法优化设计后, SHS的相位响应将得到很大提升, 进一步提高了进行气体压力测量的可行性。 与目前最常用的基于F-P谐振腔的光学干涉法相比, SHS系统虽然由于光谱分辨率相较更低, 测量精度有所不及, 但SHS系统结构简单而且对加工和装配的工艺要求没有F-P谐振腔那么高, 因此成本更低, 而且SHS系统还具有多谱线同时测量的能力, 这使得SHS仪器可以基于波长与相位之间的定量关系实现实时的相位自标定, 而且可以利用不同气体成分光谱吸收率的差异进行成分探测, 为分压力测量带来可能。 本文主要集中于理论和仿真研究, 探讨验证了利用SHS进行气体压力测量的可行性, 搭建实验平台, 基于实验测量进行更深入的对比研究将是接下来的主要工作方向。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|