本文使用的r波段信噪比大于30的恒星光谱数据, 共有A型、 B型、 dM型、 F型、 G型、 gM型、 K型7类, 波长覆盖范围为3 801~7 896 Å , 共4 096 Å , 每类恒星光谱数据共2 000条。 对恒星光谱进行归一化处理的原因有两个: ①消除差异。 天体自身亮度不同、 距地球的距离也不同, 这就导致望远镜观测天体时获取到的能量也不同, 间接导致恒星光谱数据间的差异很大, 归一化处理可以保证模型训练时的稳定性, 消除天体亮度和望远镜曝光时间造成的光谱差异。 ②获取相同的尺度。 恒星光谱的维度较高, 对恒星光谱进行归一化处理, 将流量强度转换至0~1之间, 可以很好地保留完整的光谱信息, 且以相同的尺度来比较恒星光谱间的差异。 本文使用如式(1)的线性归一化函数对恒星光谱做归一化处理。

Flux=flux-fluxminfluxmax-fluxmin(1)

式(1)中, Flux表示归一化后的光谱流量, flux表示原始光谱数据, flux_max、 flux_min分别表示原始光谱流量的最大值和最小值。 归一化后的恒星光谱, 如图5每幅小图中的最上方图所示。

光从天体发出到望远镜接收的过程中, 会受到大气湍流等自然因素的影响, 导致天体光谱数据掺杂一定的噪声; 另外, 巡天望远镜自身的局限性也是光谱掺杂噪声的一个重要原因。 虽然巡天设备的PipeLine会对天体光谱做一些去噪处理, 但并没有达到彻底去噪的程度。 因此需要对天体光谱做进一步的去噪处理, 最大限度避免噪声对科研工作的影响。 随着数字巡天技术的飞速发展, 获取海量的恒星光谱数据已经成为了现实, 寻找合适的天体光谱降噪算法已然成为一个重要的课题。

天体光谱的噪声多是狭窄的天光线以及脉冲噪声, 本文使用Ces算法^[13]对恒星光谱做去噪处理, 以降低天光线和脉冲噪声的影响。 记去噪后的光谱为de_flux, 去噪后的恒星光谱如图5每幅小图中的中间图所示。

为了将恒星光谱数据更好地放进ResNet模型, 本层对光谱进行数据转换。 我们将一条恒星光谱使用三次, 每次形成一个灰度图像, 每个灰度图像单独作为一个通道, 最后合成一个三通道的RGB图像, 也就是说一条光谱变成了一个图片。 原始A、 B、 dM、 F、 G、 gM、 K型恒星光谱如图2所示(图片来自LAMOST官网), 转换后的光谱数据如图3所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 原始恒星光谱图Fig.2 Spectral diagram of the original star

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 转换后的光谱数据图Fig.3 Spectrum data after conversion

对LAMOST产出光谱来说, 由于连续谱没有做流量定标, 因此谱线是最有效信息。 连续谱本身并不是无效信息, 其形状由天体自身的有效温度、 化学成分和表面重力加速度所决定。 不同类型的天体, 连续谱差异巨大, 如早型星、 晚型星、 致密星和类星体的连续谱, 真可谓形状各异。 在现代天体物理学中, 常采用多测光的方法来测量连续谱, 但是对于特殊类型的天体, 如有特殊发射线和吸收线的天体, 需要采用更精确的方法来测量连续谱信息。 从图3可以看出, 虽然转换后的数据可以明显区分出是不同类型的光谱数据, 但是就单张图片数据而言, 所含噪声过多, 无法很好凸出光谱的谱线信息。 因此, 我们决定使用光谱的谱线信息做数据转换。

想要使用恒星光谱的谱线信息, 需要对恒星光谱的连续谱进行归一化处理。 本文使用11阶多项式来拟合光谱的连续谱, 记拟合连续谱为pseudo_flux。 拟合连续谱后, 便可计算恒星光谱的谱线信息, 记谱线信息为flux_ratio, 则有

flux_ratio=de_fluxpseudo_flux(2)

连续谱归一化后的恒星光谱, 如图5每幅小图中的最下方图所示。

使用谱线信息转换后的光谱数据如图4所示。 需要说明的是, 图3和图4所涉及的数据转换并不涉及繁杂的算法, 只是将一维的光谱向量以图像的形式展现了出来, 对原始流量没有任何的破坏。 图3和图4的每一个像素点对应着原始恒星光谱的一个流量值。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 使用谱线信息转换后的光谱数据图Fig.4 Spectral data converted using spectral line information

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 恒星光谱处理过程展示图Fig.5 Shows the processing of stellar spectra

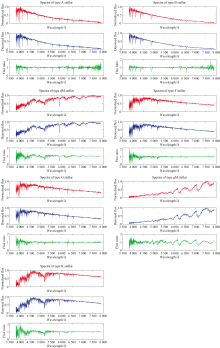
恒星光谱经流量归一化、 去噪和连续谱归一化处理后的图片如图5所示, 7张图片依次对应A、 B、 dM、 F、 G、 gM、 K型恒星光谱。

为了验证数据转换是否可行, 我们依据光谱的重要谱线信息进行检验。 对于A型恒星光谱, 其在4 102.89 Å 处有一条明显的Hσ 吸收线, 在4 341.68 Å 处有一条明显的Hγ 吸收线, 在4 862.68 Å 处有一条明显的Hb吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线, 在6 564.1 Å 处有一条明显的Hα 吸收线; 对于B型恒星光谱, 其在4 102.89 Å 处有一条明显的Hσ 吸收线, 在4 341.68 Å 处有一条明显的Hγ 吸收线, 在4 862.68 Å 处有一条明显的Hβ 吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线, 在6 564.1 Å 处有一条明显的Hα 吸收线; 对于dM型恒星光谱, 其在4 960.214 Å 处有一条明显的OIII发射线, 在4 227.92 Å 处有一条明显的CaI吸收线, 在5 176.7 Å 处有一条明显的Mg吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线; 对于F型恒星光谱, 其在6 301.943 Å 处有一条明显的OI发射线, 在4 862.68 Å 处有一条明显的Hβ 吸收线, 在5 176.7 Å 处有一条明显的Mg吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 564.61 Å 处有一条明显的Hα 吸收线; 对于G型恒星光谱, 其在6 301.943 Å 处有一条明显的OI发射线, 在4 102.89 Å 处有一条明显的Hσ 吸收线, 在4 227.92 Å 处有一条明显的Hβ 吸收线, 在4 862.68 Å 处有一条明显的Hb吸收线, 在5 176.7 Å 处有一条明显的Mg吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线, 在6 564.61 Å 处有一条明显的Hα 吸收线; 对于gM型恒星光谱, 其在4 960.3 Å 处有一条明显的OIII吸收线, 在5 176.7 Å 处有一条明显的Mg吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线, 在6 564.1 Å 处有一条明显的Hα 吸收线, 在6 718.29 Å 处有一条明显的SII吸收线; 对于K型恒星光谱, 其在4 364.378 Å 处有一条明显的OIII发射线, 在6 301.943 Å 处有一条明显的OI发射线, 在4 227.92 Å 处有一条明显的CaI吸收线, 在5 176.7 Å 处有一条明显的Mg吸收线, 在5 895.6 Å 处有一条明显的Na吸收线, 在6 302.05 Å 处有一条明显的OI吸收线, 在6 564.1 Å 处有一条明显的Hα 吸收线。

以上吸收线和发射线, 均是该类恒星光谱的重要谱线特征, 本节所述“ 检验” , 即看这些特征是否都体现在转换后的RGB图像中。 对于图像数据, 像素值越低, 图片颜色越深, 相反, 像素值越高, 图片颜色越浅。 在恒星光谱中, 吸收线对应低流量值, 发射线对应高流量值, 因此吸收线在图片中“ 颜色” 更深, 发射线在图片中“ 颜色” 更浅。 图6即为本次的实验结果。 在图6中, 从左至右依次为A、 B、 dM、 F、 G、 gM、 K型恒星光谱, 绿色圆圈标注位为恒星光谱的吸收线特征, 红色圆圈标注位为恒星光谱的发射线特征。 就A型恒星光谱来说, 上文所述的吸收线特征按从左至右, 从上至下的顺序体现在图片中, 也就是说, 光谱特征按列写入到图片中去。 其他类型的光谱也是按此规律进行标注的。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 谱线信息展示图Fig.6 Spectral line information display diagram

从图6可以看出, 绿色圆圈位置的像素点颜色较深, 红色圆圈位置的像素点较浅。 因此, 本文的数据转换是较成功的, 转换后的数据可以很好凸显出原始光谱特征, 吸收线和发射线信息很好地表现出来了。

1.4.1 结构图

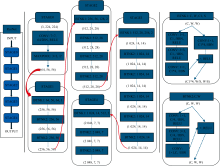
本文使用的ResNet模型, 共有5个Stage层, 其中Stage 0是预处理层, Stage 1有3个Bottleneck操作, Stage 2有4个Bottleneck操作, Stage 3有6个Bottleneck操作, Stage 4 有3个Bottleneck操作。 模型结构如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 ResNet模型图Fig.7 ResNet model diagram

1.4.2 模型介绍

Stage 0层的输入设置为(3, 224, 224), 即输入的通道数是3, 输入数据的高、 宽最高是224。 本层卷积核尺寸为7× 7, 共有64个卷积核, 卷积核步长是2, 使用的是ReLU激活函数。 最大池化函数的kernel大小是3× 3, 步长是2。 本层的输出设置为(64, 56, 56)。

由于接下来的4个Stage层由BottleNeck操作构成, 因此先介绍BottleNeck操作。 BottleNeck操作有两个: BottleNeck1和BottleNeck2。 BottleNeck2共有3个可变参数: 输入数据的通道数、 数据的高和数据的宽。 设输入数据为x, 记卷积等相关操作为τ (x), 则ReLU激活函数对τ (x)+x处理后就是BottleNeck2的输出。 需要说明的是, BottleNeck2操作的输入和输出的形状是一样的。 BottleNeck1共有5个可变参数: 输入数据的通道数、 数据的高、 数据的宽、 C1和S。 相较BottleNeck2来说, BottleNeck1多了一个卷积操作, 记这个卷积操作为δ (x)。 如果说BottleNeck2是为了避免数据维度发生变化, 那么BottleNeck1就是为数据维度发生变化而设置的, 正是多出来的卷积操作, 让输入数据x变成了δ (x), 最后再对τ (x)和δ (x)进行加和计算。

Stage 1层的输入设置为(64, 56, 56), 即输入的通道数是64, 输入数据的高、 宽最高是56。 本层的输出设置为(256, 56, 56)。

Stage 2层的输入设置为(256, 56, 56), 即输入的通道数是256, 输入数据的高、 宽最高是56。 本层的输出设置为(512, 28, 28)。

Stage 3层的输入设置为(512, 28, 28), 即输入的通道数是512, 输入数据的高、 宽最高是28。 本层的输出设置为(1 024, 14, 14)。

Stage 4层的输入设置为(1 024, 14, 14), 即输入的通道数是1024, 输入数据的高、 宽最高是14。 本层的输出设置为(2 048, 7, 7)。

1.4.3 ResNet对转换数据进行特征提取

本文使用7类64× 64的合成光谱图片训练模型。 每类图片共2 000张, 其中训练集共9 800张图片, 测试集共4 200张图片。 在本节, 我们可视化了卷积层特征提取的过程。 其中, 第1, 2卷积层特征提取的A、 B、 dM、 F、 G、 gM、 K型恒星光谱如图8和图9所示。 从图8, 图9可以看出, 7类恒星光谱图发生不同程度变化, 这正是特征提取的奇妙之处: 将恒星光谱一些不明显特征变得明显, 将一些肉眼不易发现的特征, 直接体现在了特征提取图中。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 第1卷积层可视化数据图Fig.8 Visualized data diagram of the first convolution layer

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 第2卷积层可视化数据图Fig.9 Visualized data diagram of the second convolution layer

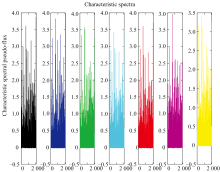
特征提取后的恒星光谱数据如图10所示, 也即ResNet模型最后一个卷积层的输出。 特征提取最终的输出是一个1× 2 048的向量, 可以发现, 经过ResNet的特征提取, 恒星光谱的维度由4 096变为了2 048。 换言之, 一个4 096维的恒星光谱, 将由一个2 048维的向量替代。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 特征提取后的恒星光谱数据Fig.10 Star spectral data after feature extraction

所谓Softmax函数, 即我们常说的归一化指数函数, 它源于sigmoid二分类函数, 是为了适应多分类任务不断推广出来的。 现如今, 在搭建“ 多分类任务” 网时, 其常用作最后一层进行最终的分类。 Softmax函数如式(3)所示

Softmax(xi)=exi∑i=1nexi∈(0, 1(3)

相较于使用最普通的max()方法, Softmax函数的优势在于融合使用了e的幂函数, 这样可以更好的做到“ 两极分化” : Softmax让正样本的结果更接近1, 负样本的结果更接近0。 需要说明的是, 样本绝对值越大, “ 两极分化” 现象越明显。

在本文中, 使用交叉熵作为损失函数来对模型进行评估, 计算方式如式(4)。

loss=-1n∑i=1n∑j=1myijlogaij(4)

式(4)中, n是样本数, m是分类数, y是标签值, a是预测值。

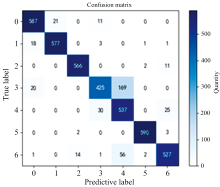
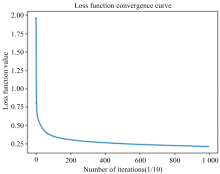
在前文的论述中, 我们详细介绍了RN-SM算法的搭建过程, 并且介绍了数据的处理过程。 在本节中, 我们选用r波段信噪比大于30的高质量恒星光谱数据进行实验, 以检验RN-SM算法的性能。 其中, A、 B、 dM、 F、 G、 gM、 K型恒星光谱各2000条。 在SoftMax层, 训练集数据∶ 测试集数据=7∶ 3。 本次实验结果如表1所示, 混淆矩阵如图11所示, 损失函数收敛曲线如图12所示。

表1

Table 1

表1(Table 1)

表1 各分类指标展示表 Table 1 Classification experiment each classification index results display table 类型 Acc Prec Recall F1 Test_acc A 0.983 0.938 0.948 0.943 0.91 B 0.99 0.965 0.962 0.963 dM 0.993 0.973 0.978 0.975 F 0.944 0.904 0.692 0.784 G 0.933 0.705 0.907 0.793 gM 0.998 0.992 0.992 0.992 K 0.973 0.929 0.877 0.902

表1 各分类指标展示表 Table 1 Classification experiment each classification index results display table

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 分类实验混淆矩阵Fig.11 Confusion matrix of classification experiment

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 损失函数收敛曲线图Fig.12 Convergence diagram of loss function

表1中的实验结果, 四舍五入取小数点后3位。 从本次实验可以看出, RN-SM算法测试集分类正确率为0.91。 本次实验中, G型恒星光谱对应的分类指标有3个偏低, F型恒星光谱对应的分类指标有2个偏低, 此种现象或许是以下两个原因导致的: (1)虽然选择的数据r波段信噪比均大于30, 但是相对于其他类型的恒星光谱, 这两个类型光谱数据的信噪比还是偏低。 (2)F、 G型恒星光谱, 相较于其他类型的恒星光谱是不太好用的数据, 这可能是观测设备自身的一些局限性导致F、 G型恒星光谱的观测、 导出不准确。

CNN作为最经典的卷积神经网络, 在诸多领域已大放异彩。 在本节中, 我们将其作为特征提取器, 并同经典机器学习算法结合使用来对本文的恒星光谱数据进行分类, 以对比本文提出的RN-SM算法的性能。 使用的经典机器学习算法有: 贝叶斯算法(Bayes)、 K近邻算法(Knn)、 支持向量机算法(SVM)、 Adaboost算法和随机森林算法(RF)。

CNN算法由四部分组成: 输入层、 卷积层、 池化层和全连接层, 卷积层是CNN算法的核心控制层, 卷积的计算如式(5)和式(6)。

xq(τ)=∑p∈Nqγp(τ-1)δpq(τ)+ετ(5)

γpτ=ReLU(xq(τ))=max(0, xq(τ))(6)

其中, τ 是网络的层数, q是特征数, δ 为卷积核, ε 为偏置, ReLU是激活函数。

在本节中, 我们将全部恒星光谱整合成数据矩阵, 一次性全部输入至模型中, 数据矩阵的一行代表一条恒星光谱。 卷积层对数据矩阵进行卷积操作, 以生成“ 卷积数据” 。 池化层可以降低数据矩阵的规模, 这样就可以让“ 卷积数据” 的维度减小, 方便算法的运行。 池化层以最大池化方法, 保留了数据矩阵的局部信息, 产生的池化数据矩阵最终输入至全连接层进行整合重组, 重组后的数据输入至经典机器学习算法中进行自动分类。 本次实验结果如表2所示。 表2中实验结果, 四舍五入取小数点后3位。

表2

Table 2

表2(Table 2)

表2 对比算法的分类正确率 Table 2 Classification accuracy of comparison algorithm 算法 CNN+ Bayes CNN+ Knn CNN+ SVM CNN+ Adaboost CNN+ RF 分类正确率 0.862 0.876 0.894 0.868 0.889

表2 对比算法的分类正确率 Table 2 Classification accuracy of comparison algorithm

可以看出, 在众多对比算法中以CNN+SVM的分类正确率最高, 为0.894, 然而这一分类正确率还是低于RN-SM算法的分类正确率。 因此认为, 本文提出的RN-SM算法具有一定的实践应用基础, 可以很好服务于恒星光谱分类任务。

信噪比是衡量天体光谱质量的参数, 信噪比越高, 天体光谱的质量越好, 相反, 信噪比越低, 天体光谱的质量越差。 LAMOST产出光谱共有u、 g、 r、 i、 z五个波段, 本文仅使用其r波段信噪比。 在上一节中, 我们考察了RN-SM算法使用r波段信噪比大于30数据时的性能。 在本节中, 我们依据r波段信噪比, 将数据分为3组: (0, 10), (10, 20)和(20, 30)来考察使用不同信噪比数据对RN-SM算法的影响。 除(10, 20)区间的B型数据1 603条, (20, 30)区间的B型数据850条外, 其余每个区间, 每类恒星光谱选用2 000条数据。 对比算法同为2.2节所述算法。 本次实验结果如表3、 表4所示。 表3和表4中的实验结果, 四舍五入取小数点后3位。

表3

Table 3

表3(Table 3)

表3 不同的信噪比数据分类指标结果 Table 3 Classification index results of different signal-to-noise ratio data 信噪比 类型 Acc Prec Recall F1 Test_acc (0, 10) A 0.95 0.845 0.806 0.825 0.79 B 0.931 0.716 0.704 0.71 dM 0.984 0.939 0.956 0.947 F 0.904 0.772 0.477 0.59 G 0.875 0.556 0.858 0.674 gM 0.992 0.982 0.96 0.971 K 0.941 0.843 0.74 0.788 (10, 20) A 0.96 0.886 0.861 0.873 0.85 B 0.969 0.796 0.72 0.756 dM 0.987 0.956 0.959 0.957 F 0.915 0.706 0.775 0.739 G 0.919 0.75 0.727 0.738 gM 0.993 0.979 0.976 0.978 K 0.956 0.857 0.86 0.859 (20, 30) A 0.978 0.93 0.913 0.922 0.89 B 0.984 0.931 0.958 0.944 dM 0.991 0.955 0.98 0.967 F 0.937 0.902 0.613 0.73 G 0.922 0.647 0.922 0.761 gM 0.997 0.992 0.99 0.991 K 0.97 0.954 0.846 0.879

表3 不同的信噪比数据分类指标结果 Table 3 Classification index results of different signal-to-noise ratio data

表4

Table 4

表4(Table 4)

表4 不同信噪比数据对比算法分类正确率 Table 4 Classification accuracy rate of different SNR data comparison algorithm 信噪比 算法 CNN+Bayes CNN+Knn CNN+SVM CNN+Adaboost CNN+RF (0, 10) 0.58 0.71 0.74 0.72 0.75 (10, 20) 分类正确率 0.69 0.79 0.81 0.81 0.82 (20, 30) 0.79 0.85 0.85 0.82 0.86

表4 不同信噪比数据对比算法分类正确率 Table 4 Classification accuracy rate of different SNR data comparison algorithm

由表3可以看出, 随着数据质量的提高, RN-SM算法的分类正确率也在提高, 即RN-SM算法受约束于数据的信噪比。 从表3也可以看出, F、 G型恒星光谱对应的分类指标共有2~3个偏低, 再次证实了2.1节所述的猜想。 由表4可以看出, 随着信噪比的提高, 各对比算法的分类正确率也在提高, 但是, 四个区间波段对应的分类正确率均低于RN-SM算法的分类正确率。 因此认为, 本文提出的RN-SM算法具有一定的实践应用基础, 可以很好服务于恒星光谱分类任务。