作者简介: 吴云龙, 2000年生,南京航空航天大学硕士研究生 e-mail: ylwu@nuaa.edu.cn
X射线的能谱信息在计算机断层扫描(CT)中有重要应用, 准确的能谱信息可以帮助实现能谱CT, 并对传统CT重建中因射束硬化造成的伪影进行有效校正等。 在涉及CT成像的领域, 如医学成像和工业检测等, 大多数应用中都使用高功率X射线管。 这种X射线管可以在短时间内产生大量的X射线, 从而提高成像效率, 并获取高分辨率和高清晰度的图像。 然而, 由于高功率X射线管的出射光子通量过高, 直接测量其能谱变得较为困难。 目前, 常用的能谱获取方法是能谱估计, 该方法通过获取不同厚度模体的投影数据, 建立能谱、 衰减系数与投影数据之间的方程组, 最终求解该方程组以获得能谱。 能谱估计的方法依赖于算法和数据的准确性, 由于方程的严重病态, 在缺乏初始值的情况下, 求解出的能谱会缺失重要的特征信息。 为此, 提出了一种结合直接测量和神经网络模型预测的新方法。 通过使用一定厚度的铁片降低X射线的光子通量, 使其达到探测器可检测的水平, 然后逐步添加薄厚度的铁片, 获取一系列能谱数据。 这些数据用于训练神经网络模型, 以精准预测出射能谱。 仿真数据的测试结果表明, 所提神经网络模型在预测能谱方面表现优异, 归一化后的预测能谱与真实值之间的均方根误差仅为0.000 031。 然而, 由于实验条件的限制, 实测数据量相对较少, 为了提升模型的广泛适用性和预测精度, 研究进一步结合了迁移学习的方法。 首先, 利用大量的GEANT4模拟数据训练神经网络, 然后通过实验测得的少量能谱数据对模型进行微调。 实验数据的预测结果显示, 归一化后的能谱与真实值的均方根误差为0.000 194。 与传统的能谱估计方法相比, 所提出的方法不仅在精度上有显著提升, 而且还能准确捕捉到能谱的重要特征信息。 这一方法的优势在于通过神经网络强大的学习能力, 克服了传统方法对初始值和病态方程求解的依赖, 从而大大提高了预测的稳定性与准确性。 仿真数据和实验数据均验证了该方法的可行性。
The energy spectrum of X-rays plays a critical role in computed tomography (CT) applications. Accurate spectral information is crucial for implementing spectral CT and effectively correcting artifacts resulting from beam hardening in conventional CT reconstruction. In the fields of medical imaging and industrial inspection, high-power X-ray tubes are commonly used due to their ability to produce a large flux of X-rays in a short time, thereby improving imaging efficiency and enabling the acquisition of high-resolution and high-contrast images. However, directly measuring the energy spectrum of high-power X-ray tubes becomes challenging due to their excessively high photon flux.Currently, energy spectrum estimation is the predominant method for obtaining spectral information. This approach involves acquiring projection data from phantoms of varying thicknesses and establishing a system of equations that relate the spectrum, attenuation coefficients, and projection data. By solving this system, the energy spectrum can be obtained. However, the accuracy of this method relies heavily on the precision of algorithms and data. Due to the severely ill-posed nature of the equations, the reconstructed spectrum often lacks critical spectral features when suitable initial values are not provided. To address this limitation, this study proposes a novel method that combines direct measurement with neural network-based prediction. The photon flux of the X-rays is reduced to a detectable level by introducing a certain thickness of iron filters. A series of spectral data is then acquired by sequentially adding thin iron filters of varying thicknesses. These data are used to train a neural network model, enabling precise prediction of the emitted energy spectrum. Simulation results demonstrate the outstanding performance of the proposed neural network model in predicting energy spectra, achieving a root mean square error (RMSE) of only 0.000 031 between the normalized predicted spectrum and the ground truth. However, due to experimental limitations, the amount of measured data is relatively small. To enhance the model's generalizability and prediction accuracy, this study integrates transfer learning. Specifically, a neural network is first trained on a large dataset generated using GEANT4 simulations, and then fine-tuned using a small amount of experimentally measured spectral data. Prediction results based on experimental data show an RMSE of 0.000 194 between the normalized predicted spectrum and the ground truth. Compared to traditional spectral estimation methods, the proposed approach not only achieves significantly higher accuracy but also effectively captures critical spectral features. The advantages of this method lie in leveraging the powerful learning capabilities of neural networks, thereby overcoming the dependency on initial values and ill-posed equation solving in traditional methods, and greatly improving prediction stability and accuracy. Both simulation and experimental results validate the feasibility of the proposed approach.
计算机断层扫描(computed tomography, CT)技术能够无损地重建被测物体的内部结构信息, 在众多领域中有着重要应用, 如医学诊断成像, 工业的无损检测等。 自CT技术问世以来, 其发展和研究一直致力于更快的成像速度和更高的成像效率, 因此成像系统一般选用高功率、 高出射通量的X射线管, 保证在短时间内能够产生大量光子[1]。 另一方面, 为了获得详细的物质成分信息实现物质分辨能力, 双能CT和多能CT的概念也被提出。 相比于传统CT, 双能CT和多能CT通过测量两个或多个能量段的衰减信息来实现物质成分识别, 以此提供更丰富的信息达到功能成像的目的, 是未来CT成像的发展方向。 获取准确的出射X射线能谱是双能和多能CT技术的基础。 尤其在医学诊断方面, 准确的X射线能谱也有利于剂量估计和控制、 修正重建图像伪影等[2]。
目前已有的X射线能谱测量方法大致分为直接法与间接法。 直接法是使用X射线光谱仪直接测量能谱[2], 但仅适用于低通量球管, CT技术使用的高功率X射线管能在短时间内产生大量具有宽能谱的光子, 直接测量会导致光谱仪死时间过大。 常见的高功率X射线管出射光子通量一般在1011~1013量级, 而探测器最大光子计数率一般在104~106量级, 因此无法直接用光谱仪测量能谱。 间接法是获得X射线穿过不同厚度材料模体的投影数据, 建立投影数据、 能谱和模体衰减系数[2]的方程组来求解能谱。 间接法是将能谱估计问题转化成病态方程组的求解问题, 关键在于解决衰减矩阵的病态性和不适定性, 对求解算法要求较高。 常用的能谱估计算法有正则化法、 降维算法、 最大似然估计法等, 正则化和降维的办法能够减轻衰减矩阵的病态性和不适定性, 但都不能较好地估计特征峰部分的能谱[3, 4, 5], 最大似然估计法可以较好地估计能谱分布, 但对迭代初始值的要求较高[6], 初始值越接近真实能谱, 结果越准确。
直接法因X射线管的高通量导致无法直接用光谱仪测量能谱, 间接法计算出的能谱特征信息会有缺失, 只能得到粗略的能谱信息。 因此, 本文提出了一种基于神经网络的能谱预测方法。 具体而言, 首先通过选择适当厚度的滤波材料, 将光子通量降低至谱仪探测器可接受的范围。 随后, 依次增加多个等厚度滤波材料, 以获取一系列能谱数据。 通过这些数据训练神经网络模型, 进而预测X射线管的出射能谱。
设X射线管的出射能谱为I, 其第i个能谱通道下的光子计数为Ii(i=1, 2, …, n), 其可以被假设为处于理想状态下(单能窄束), 因此经过厚度为d的衰减材料后, 每个通道的计数满足式(1):
式(1)中, In为出射能谱某通道下的光子计数, I'n为穿过模体后的能谱某通道下的光子计数, μ n为该能量下模体材料的质量衰减系数, d为模体厚度, ρ 为模体密度。
添加厚度为d的滤波材料, 将X射线管通量降低至探测器的适用范围内, 根据式(1), 已知模体材料厚度和衰减系数, 多能X射线出射能谱I每个通道下的光子计数都可以通过降低通量后测量到的能谱I'进行计算得到。 实际上, X射线管的出射光子束在经过准直后也并非是严格意义上的单能窄束, 再加上散射光子的影响, 导致直接使用式(1)计算每个通道下的光子计数衰减值进行能谱求解比较困难。 因此, 本文提出了使用神经网络模型来预测能谱的方法。
神经网络是一种模仿人脑神经元连接的计算模型, 广泛应用于模式识别、 数据预测等领域[7], 包括输入层、 隐藏层和输出层。 输入层接收特征数据, 隐藏层通过非线性激活函数(如ReLU、 Sigmoid等)处理信息, 输出层生成最终的预测结果[8]。 对神经网络而言, 训练数据量的大小直接影响模型的效果和泛化能力, 足够的训练数据可以帮助模型学习更全面的特征, 提升泛化能力。 在实验中, 长时间使用探测器会使探测器过热从而影响测量, 故实验数据量会比较少, 影响模型的预测效果, 因此引入迁移学习的方法。 首先使用多组模拟能谱数据进行模型训练, 再使用实验数据对网络模型进行微调, 优化模型, 提高预测能谱的准确性。 此外, 采用网格搜索的方法进行超参数优化, 调整批大小、 迭代次数、 数据集划分比例、 样本权重及随机种子等参数。 最终, 确定批大小为32、 迭代次数为4 000、 模拟数据的测试集和验证集占比分别为0.06和0.14, 模拟数据和实验数据样本权重分别为0.3和0.7, 随机种子设置为24, 以确保数据分割的可复现性。
图1展示了本文使用的三层全连接神经网络结构, 输入层接收2个特征: 滤波材料厚度和该厚度下的光子总计数。 第一个隐藏层包含32个神经元, 并使用ReLU激活函数; 第二个隐藏层包含64个神经元, 同样采用ReLU激活函数。 最后, 输出层的神经元数量设置为225, 以匹配预测能谱的长度。
仿真实验使用蒙特卡洛模拟软件GEANT4完成。 为了增加模拟效率, 仿真实验分成两部分, 第一部分为模拟产生X射线管出射谱, 第二部分为模拟X射线管出射能谱预测实验。 图2展示了X射线管出射谱模拟(第一部分实验)的几何结构, 其中绿色部分表示真空管, 白色部分为钨靶, 红色部分为CdTe探测器。 钨靶设计为面向电子枪并与水平方向形成45° 夹角的倾斜圆盘。 CdTe探测器位于钨靶的正下方, 记录CdTe探测器中的能量沉积谱。
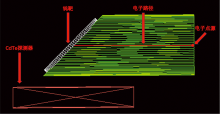 | 图2 X射线管出射谱模拟实验几何结构Fig.2 Geometric configuration of X-ray tube emission spectrum simulation experiment |
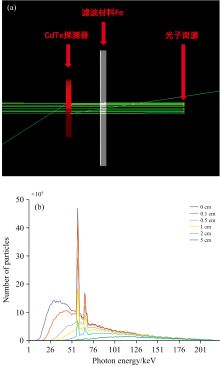
图3展示了X射线管出射谱估计模拟实验的几何结构及不同厚度下的模拟能谱。 图3(a)中红色模型为CdTe探测器, 白色模型为滤波材料Fe, 滤波材料的厚度从0变化至11 cm, 每次增加0.01 cm。 平行光束面源的中心点与CdTe探测器和滤波材料位于同一直线上, 出射光子的能量分布符合225 keV电子轰击钨靶的光谱, 记录CdTe中的能量沉积谱。 图3(b)展示了五种典型厚度的模拟能谱及原始谱。
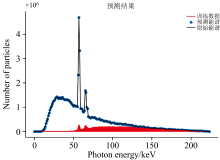
使用3~11 cm范围内的能谱数据(共555个)对模型进行训练和测试, 训练集占比为80%, 测试集占比为20%。 在归一化处理后, 预测能谱与真实值之间的均方根误差(RMSE)为0.000 031。 图4展示了预测能谱与原始能谱的对比结果。
实验在最大管电压320 kV、 最大管电流22.5 mA的德国YXLON公司MG325型X射线实时成像和图像处理系统上进行。 使用的探测器为AMETEK公司生产的X-123碲化镉探测器, 探测器的有效探测面积为25 mm2, 厚度为1 mm, 最佳能量范围为5~150 keV。 实验中设置225 kV管电压和0.05 mA管电流, 使用N200滤过(由1 mm铅, 3 mm锡和2 mm铜组成)。 实验材料为10 cm× 10 cm大小的厚度为0.1、 0.2、 0.3、 0.5和1 cm的铁片。 为了降低散射光子的干扰, 在探测器前段部分添加了铅皮屏蔽[9]。 实验中, 探测器窗口对准射线管的出口中心, 滤片到探测器距离为149 cm, 测量时间设置为120 s。 将铁片放置在探测器前, 测量1.0、 1.1、 1.2、 …、 2 cm共11组能谱数据作为神经网络的训练数据, 同时测量不放置铁片的能谱作为真实值, 用于验证求解结果的准确性。 图5展示了实验环境及设备。
实验能谱数据是探测器测量值经过探测效率修正、 死时间修正及能量刻度后得到, 探测效率数据从AMETEK公司官方网站提供的产品说明中获得, 死时间由探测器每次测量的数据给出。 能量刻度需要计算道址— 能量的对应关系, 由于探测器的增益设置能量测量范围为5~256 keV, 所以道址的选取为5 keV、 256 keV及W-74的特征能量— — Kα 1=59.310 keV、 Kα 2=57.973 keV、 Kβ 1=67.233 keV处的, 使用二项式进行拟合, 进行能量刻度。 图6(a)展示了二项式拟合后的能量刻度结果, 图中参数x为道址, A、 B、 C分别为常数项、 一次项系数和二次项系数, 图6(b)展示了修正后的实验测量数据, 0 cm指无滤波材料下的真实值能谱, 用以对比预测能谱, 1.0~2.0 cm能谱为训练数据。
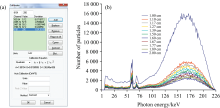 | 图6 能量刻度二项式拟合结果(a), 探测器测量到的数据经修正后的能谱数据(b)Fig.6 Energy calibration binomial fitting results (a) and corrected energy spectrum data measured by the detector (b) |
由于直接使用1~2 cm的数据训练模型会因为数据量过少而无法达到良好的训练效果, 因此采用了迁移学习的方法。 使用GEANT4仿真软件, 建立了锥形光束点源、 Fe滤波材料和CdTe探测器的几何模型。 光源的能谱分布基于实验测得的1 cm能谱数据, Fe材料的厚度设置为0~2 cm(间隔0.005 cm)和2~3 cm(间隔0.1 cm), 共测量了410个能谱数据。 图7展示了迁移学习的GEANT4模型搭建及能谱数据。 图7(a)中, 红色模型为CdTe探测器, 白色模型为滤波材料Fe, 点源锥形光束的角度为40° 。 图7(b)为模拟能谱数据。
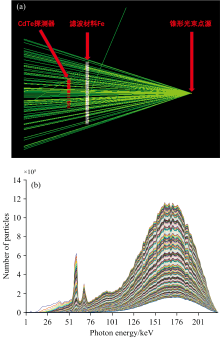 | 图7 迁移学习中使用的GEANT4模型(a), 模拟能谱训练数据(b)Fig.7 GEANT4 model used in transfer learning (a) and simulated energy spectrum training data (b) |
预测能谱的输入值为铁片厚度(0 cm)和该厚度下的总计数。 由于总计数是未知的, 需要通过GEANT4模拟数据进行计算。 在GEANT4模拟中, 0 cm铁下的光子总计数与1 cm铁下的光子总计数的比值与实验结果相近。 根据此关系, 总计数可以通过式(2)进行计算
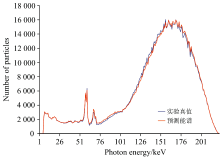
式(2)中, S0和S1为GEANT4模拟出的0 cm铁和1 cm铁下的光子总计数, T1为实验测得的1 cm铁下的光子总计数。 根据式(2)计算得到的0 cm厚度下的总计数与实验测得的数据进行对比, 误差为0.86%。 经过归一化处理后, 预测能谱与真实值的均方根误差(RMSE)为0.000 194。 图8展示了预测能谱与真实能谱的对比结果。
本文提出了一种通过神经网络模型训练能谱数据来预测X射线管出射能谱的方法。 该方法首先使用一定厚度的铁材料将X射线管的光子通量降低至谱仪探测器能够响应的范围, 然后逐步添加薄厚度的铁材料, 并在每次添加后测量一次能谱, 使用记录下的能谱数据训练神经网络模型, 预测出射能谱。 由于实验数据过少, 本文将测量到的能谱作为GEANT4模拟的光子分布, 采用迁移学习的方法, 通过使用模拟能谱进行神经网络的初步训练, 再使用实验测得的能谱对模型进行微调。 该方法可以精准预测能谱, 并且没有损失能谱信息。
在本文的实验中, 所测量的能谱来自225 keV电子轰击钨靶的X射线能谱。 考虑到对其他更高能量的能谱进行求解还需要重新测量, 因此神经网络模型的训练数据选择仍需要进一步研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|