正态分布筛选法提高近红外光谱稳定性研究

引用本文

李晓星, 肖金凤, 张洪明, 吕波, 尹相辉, 赵明, 马飞, 符佳, 胡艳, 李志豪, 王福地, 沈永才, 戴舒宇. 正态分布筛选法提高近红外光谱稳定性研究[J]. 光谱学与光谱分析, 2025,45(6): 1566-1577.
LI Xiao-xing, XIAO Jin-feng, ZHANG Hong-ming, LÜ Bo, YIN Xiang-hui, ZHAO Ming, MA Fei, FU Jia, HU Yan, LI Zhi-hao, WANG Fu-di, SHEN Yong-cai, DAI Shu-yu. Study on Improving Stability of Near-Infrared Spectra by Normal Distribution Screening Method[J]. Spectroscopy and Spectral Analysis, 2025,45(6): 1566-1577.
Doi:10.3964/j.issn.1000-0593(2025)06-1566-12 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

正态分布筛选法提高近红外光谱稳定性研究

李晓星^1,², 肖金凤^1,^*, 张洪明^2,^*, 吕波^2,^3,^*, 尹相辉¹, 赵明⁴, 马飞⁵, 符佳², 胡艳^1,², 李志豪^1,², 王福地², 沈永才⁶, 戴舒宇⁷

1.南华大学电气工程学院, 湖南衡阳 421001

2.中国科学院合肥物质科学研究院等离子体物理研究所, 安徽合肥 230031

3.中国科学技术大学研究生院科学岛分院, 安徽合肥 230031

4.安徽工程大学生物与食品工程学院, 安徽合肥 241000

5.合肥工业大学食品与生物工程学院, 安徽合肥 230009

6.合肥师范学院物理与材料工程学院, 安徽合肥 230601

7.大连理工大学物理学院, 辽宁大连 116024

*通讯作者 e-mail: 806609919@qq.com; hmzhang@ipp.ac.cn; blu@ipp.ac.cn

作者简介: 李晓星, 1999年生,南华大学电气工程学院硕士研究生 e-mail: xiaoxing.li@ipp.ac.cn

收稿日期: 2024-07-25 修订日期: 2024-12-21

基金: 国家自然科学基金项目(32372357)),安徽省教育厅优青基金项目(2022AH030097),磁约束聚变安徽省实验室开放基金项目(2023AMF03005),湖南省教育厅科研项目(21B0439)资助

摘要

在发酵过程的近红外在线检测中, 由于发酵液中需要持续通入氧气来促进微生物的生长和代谢活动, 常会在发酵液中产生气泡。发酵液中的气泡经过探头前方时, 会对近红外光谱的强度产生较大干扰。为了剔除发酵液近红外在线检测过程中采集到的气泡引起的异常光谱, 减少光谱波动, 提出了一种正态分布筛选方法。制备了600 g质量分数为10%的葡萄糖溶液, 每隔30 s加2 g葡萄糖溶液至盛有600 mL蒸馏水的反应釜中, 搅拌均匀, 然后计算和记录反应釜内葡萄糖溶液的质量分数, 并在反应釜底部通入氧气产生气泡, 利用近红外光谱仪采集反应釜内葡萄糖溶液的近红外光谱。分别采用主成分分析(principal component analysis, PCA)结合马氏距离法, 欧氏距离法, 孤立森林, 正态分布筛选法对受到气泡影响的异常光谱剔除后, 将光谱样本集按照4∶1的比例随机划分为校正集和预测集, 随后经过光谱预处理, 利用偏最小二乘法(partial least squares, PLS)对校正集建立葡萄糖溶液浓度预测模型, 并用建立的PLS模型对预测集进行预测。通过校正集相关系数, 校正集均方根误差, 以及预测集的相关系数和均方根误差进行对比分析。采用四种方法剔除受到气泡影响的异常光谱后, 所建模型结果如下, PCA结合马氏距离法剔除异常光谱后得到的校正集相关系数Rc2为0.998 208, 均方根误差RMSECV为0.000 764, 预测集相关系数Rp2为0.997 994, 均方根误差RMSEP为0.000 764; 欧式距离法剔除异常光谱后得到的校正集Rc2为0.998 628, 均方根误差RMSECV为0.000 652, 预测集相关系数Rp2为0.998 628, 均方根误差RMSEP为0.000 655; 孤立森林剔除异常光谱后得到的校正集Rc2为0.998 255, RMSECV为0.000 739, 预测集Rp2为0.998 132, RMSEP为0.000 740; 正态分布筛选方法剔除异常光谱后得到的校正集Rc2为0.998 641, 均方根误差RMSECV为0.000 645, 预测集Rp2为0.998 628, RMSEP为0.000 636。结果表明: 对比四种方法, 采用正态分布筛选方法能有效减少光谱强度的波动, 剔除异常光谱较其他方法效果更佳。

关键词: 近红外光谱; 异常光谱剔除; 马氏距离; 正态分布筛选法

中图分类号:O439 文献标志码:A

Study on Improving Stability of Near-Infrared Spectra by Normal Distribution Screening Method

LI Xiao-xing^1,², XIAO Jin-feng^1,^*, ZHANG Hong-ming^2,^*, LÜ Bo^2,^3,^*, YIN Xiang-hui¹, ZHAO Ming⁴, MA Fei⁵, FU Jia², HU Yan^1,², LI Zhi-hao^1,², WANG Fu-di², SHEN Yong-cai⁶, DAI Shu-yu⁷

1. College of Electrical Engineering, University of South China, Hengyang 421001, China

2. Institute of Plasma Physics, Hefei Institutes of Physical Sciences, Chinese Academy of Sciences, Hefei 230031, China

3. Science Island Branch, Graduate School, University of Science and Technology of China, Hefei 230031, China

4. College of Biological and Food Engineering, Anhui Polytechnic University, Hefei 241000, China

5. College of Food and Biological Engineering, Hefei University of Technology, Hefei 230009, China

6. College of Physics and Materials Engineering, Hefei Normal University, Hefei 230601, China

7. College of Physics, Dalian University of Technology, Dalian 116024, China

*Corresponding authors

Abstract

In the near-infrared online detection of the fermentation process, bubbles are often generated in the fermentation broth due to the need to continuously pass oxygen into the fermentation broth to promote microbial growth and metabolic activities. When the bubbles in the fermentation broth pass in front of the probe, they will interfere with the intensity of the near-infrared (NIR) spectrum. To eliminate the abnormal spectra caused by bubbles collected during the near-infrared online detection of fermentation broth and reduce spectral fluctuations, a normal distribution screening method is proposed in this study. In this study, 600 g of glucose solution with a mass fraction of 10% was prepared, adding 2 g of glucose solution to a reactor containing 600 mL of distilled water every 30 s, stirring well, then calculating and recording the mass fraction of glucose solution in the reactor, and generating bubbles by passing oxygen to the bottom of the reactor, and collecting the NIR spectra of the glucose solution in the reactor by using NIR spectrometer, respectively. After the anomalous spectra affected by the air bubbles were excluded by principal component analysis (PCA) combined with Mahalanobis distance method, Euclidean distance method, isolated forest, and normal distribution screening method, the sample set of spectra was randomly divided into the correction set and the prediction set according to the ratio of 4∶1, and then, after the spectral pre-processing, the glucose concentration prediction model was established for the correction set using the partial least squares method (PLSR) and the prediction set was analyzed by the established PLSR model. The correlation coefficient of the correction set, the root mean square error of the correction set, and the correlation coefficient and root mean square error of the prediction set were compared and analyzed. The results of the constructed model after removing the anomalous spectra affected by bubbles using the four methods are as follows: the correlation coefficientRc2 of the correction set obtained after removing the anomalous spectra by PCA combined with the Mahalanobis Distance Method is 0.998 208, and the root-mean-square error RMSECV is 0.000 764, and the correlation coefficientRp2 of the prediction set is 0.997 994, and the root-mean-square error RMSEP is 0.000 764; The correction setRc2 obtained after removing the anomalous spectra by the Euclidean distance method is 0.998 628, the root mean square error RMSECV is 0.000 652, the prediction set correlation coefficientRp2 is 0.998 628, and the root mean square error RMSEP is 0.000 655; the correction setRc2 obtained after removing the anomalous spectra by the isolated forest method is 0.998 255, the RMSECV is 0.000 739, the prediction setRp2 is 0.998 132, and the RMSEP is 0.000 740; the correction setRc2 obtained after the removal of anomalous spectra by the normal distribution screening method is 0.998 641, with a root mean square error RMSECV of 0.000 645, and the prediction setRp2 is 0.998 628, with a RMSEP of 0.000 636. Comparing the four methods, the normal distribution screening method can effectively reduce the fluctuation of spectral intensity and eliminate abnormal spectra more effectively than other methods.

Keyword: Near-infrared spectroscopy; Abnormal spectrum removal; Mahalanobis distance; Normal distribution screening method

文章图片

引言

近红外光谱(near infrared spectroscopy, NIRS)是一种高效便捷的光谱分析技术, 利用含氢官能团振动光谱特征进行分析, 获取丰富的物质内部信息。与传统分析方法相比, NIRS具备快速、简便、无试剂消耗、无环境污染、不受样品形态限制、支持多组分同时检测等优点, 极大地提升了分析效率和数据可靠性。在发酵过程的监测与控制中, NIRS能够即时监测关键的工艺参数, 减少人力成本, 提高生产效率, 展现出其独特的优势^[1]。

但是在发酵过程中, 为了保证发酵液中微生物的生长和代谢活动, 常常会在发酵罐中持续通入氧气, 通氧气所产生的气泡可能会使得近红外光谱吸收峰的强度发生剧烈波动, 影响光谱分析的定量结果, 因此在使用近红外光谱定量分析建模和预测前, 需要尽可能剔除光谱数据中的异常样本, 减少光谱的波动。

目前国内外已经开展了一些关于近红外光谱异常样本剔除的研究。龙若兰等采用马氏距离结合主成分分析对近红外光谱进行异常样本剔除^[2]。石鲁珍等选取一阶导数前4个主成分的得分进行马氏距离计算, 将大于阈值的异常光谱样品剔除, 用剩下的样品建立模型, 预测精度相较于剔除前得到明显的改善^[3]。 Zhang等基于正常样本建立的交互预测模型和疑似异常样本的独立验证, 提出了一种增强的蒙特卡罗界外样本识别方法^[4]。 Chen等在模型集群分析算法的基础上提出了采样误差分布分析算法, 可用于异常样本的筛选^[5]。王亚栋等基于欧氏距离结合3σ 法则对异常样本进行迭代剔除^[6]。罗林等采用马氏距离对酒醅水分近红外光谱进行异常样品识别及剔除, 建立了酒醅水分近红外定量分析模型, 预测相关系数提高了0.43%, 预测均方根误差下降了0.2%^[7]。陈斌等采用主成分分析法结合马氏距离法对近红外校正样品集中的异常样品进行剔除, 从校正集的60个食醋样本中剔除了12个异常样本, 建立了总酸的模型, 比起剔除前, 总酸和挥发酸预测均方根误差RMSEP分别降低了1.546%和2.420%^[8]。

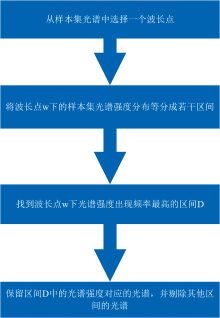
为了剔除发酵液近红外在线检测过程中采集到的气泡引起的异常光谱, 减少光谱波动, 本研究提出了一种正态分布筛选方法, 将某一波长的光谱强度分布等分为若干个区间, 根据单一波长光谱强度近似符合正态分布的特性, 找到光谱强度出现频率最高的区间, 保留该区间内的光谱强度对应的光谱, 以达到剔除异常数据的目的。研究过程中以葡萄糖溶液为研究对象, 对比正态分布筛选方法与不同异常样本筛选方法处理样本集后的建模效果, 验证正态分布筛选方法剔除异常光谱的能力。

1 异常光谱剔除方法研究

在近红外光谱定量分析时, 气泡可能会导致光谱数据中出现异常值, 扭曲光谱数据与被测组分浓度之间的关系, 降低校准模型的准确性和鲁棒性, 故在建模和预测之前需要对这些异常光谱进行剔除。综合之前的文献, 有主成分分析结合马氏距离法、欧式距离法、孤立森林法等异常数据筛选的方法。针对发酵液中异常样本的筛选方法, 本研究基于采集到的近红外光谱单一波长的光谱强度近似符合正态分布, 提出一种正态分布筛选方法。首先对各种方法的理论和计算方法进行简介。

1.1 PCA结合马氏距离法剔除异常光谱

PCA是一种常用的数据降维技术, 通过将高维度数据映射到低维空间, 从而减少数据的维度, 在保留尽可能多的信息的同时, 消除众多信息共存中相互重叠的信息部分。

马氏距离法是一种用来衡量点与分布之间距离的度量方法, 它考虑了数据分布的协方差, 使得不同维度上数值差异对距离的影响得到了合理调整^[9]。

PCA方法得到光谱的主成分和得分, 得分为压缩后的光谱数据, 使用得分数据代替原始光谱数据计算马氏距离, 不仅能够反映全谱数据信息, 而且也能压缩用于计算马氏距离的变量数, 并且能够保证协方差矩阵不存在共线问题。

使用PCA结合马氏距离法剔除异常光谱, 通常需要分析不同的马氏距离百分位阈值条件下模型的预测效果。通过模型评价指标评估剔除异常样本后的模型性能, 从而选择最优的百分位阈值, 以确保模型在未知数据集上的预测能力和泛化能力达到最佳状态。

1.2 欧式距离法剔除异常光谱

欧氏距离是一种在多维空间中度量两个点之间直线距离的方法, 基于欧几里得中两点之间的距离公式进行计算。光谱数据包含许多波段的反射率或吸收率信息, 这些信息可以被看作多维空间中的一个点。每一条光谱数据可以被表示为一个向量, 而向量之间的欧式距离则可以量化这些光谱之间的相似度或差异性。

欧式距离法剔除异常光谱具体步骤如下^[7]:

Step 1: 计算光谱数据集的平均光谱, 平均光谱代表了光谱数据集的综合属性, 能反映数据的总体趋势;

Step 2: 根据欧式距离公式计算各样本光谱到平均光谱的欧式距离;

Step 3: 利用3-sigma准则设定欧式距离阈值;

Step 4: 将各样本光谱到平均光谱的欧式距离与阈值比较, 如果大于阈值, 即判定该光谱为异常光谱并剔除;

Step 5: 剔除异常光谱后, 需要重新计算新的数据集的平均光谱, 并重复以上步骤, 直至数据集中不再存在异常样本。

1.3 孤立森林剔除异常光谱

孤立森林算法的基本理念是异常数据偏离大部分数据, 往往在较少的分割操作之后就会被有效地孤立^[10]。

算法的构建过程如下: 首先, 从原始数据集中随机选取一部分样本, 将其作为根节点; 然后, 在每个节点处, 随机选择一个特征, 并以该特征的某个值作为切割点, 生成一棵二叉树。这个过程会不断重复, 直到达到二叉树的最大深度限制, 或者该节点的子节点只有一个数据样本。这样, 每一棵iTree都是孤立的, 并且具有不同的特征切割点, 用生成的孤立树来评估测试数据, 即计算异常分数s, 见式(1)^[11]

$s (x, φ) = 2^{- \frac{E (h (x))}{c (φ)}}$ (1)

式(1)中: c(φ )为给定样本数φ 时路径长度的平均值, 用来对样本x的路径长度h(x)进行标准化处理, h(x)为x在每棵树的高度。 s越接近1, 则其是异常点的可能性越高; s远小于0.5, 则一定不是异常点; s在0.5附近, 数据极不可能是异常点。

1.4 正态分布筛选法剔除异常光谱

一般来说, 对于采集到的光谱, 如果测量次数足够多, 且光谱强度的变化主要是由于随机误差引起的, 那么依据中心极限定理, 光谱在某一个波长的光谱强度是近似符合正态分布的, 如图1所示。所以提出一种正态分布筛选方法, 具体步骤如下:

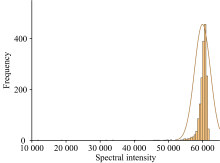	Figure Option View Download New Window
	图1 样本光谱中某一波长的光谱强度分布Fig.1 Spectral intensity distribution at a specific wavelength in the sample spectrum

Step 1: 从筛选前的样本集光谱中选择其中一个波长w, 得到筛选前的样本集光谱在该波长的光谱强度;

Step 2: 将波长w下的光谱强度分布等分为若干个区间;

Step 3: 统计每一个区间上的光谱强度出现频率, 找到波长为w的光谱强度出现频率最高的区间D;

Step 4: 将区间D中的光谱强度对应的光谱保留下来, 并剔除其他区间的光谱。

研究表明, 选择不同的波长以及等分区间数量会直接影响剔除异常光谱的效果和预测模型的性能。因此使用正态分布筛选法时, 需要采用控制变量法, 分别分析不同波长和等分区间数量下得到的模型的预测结果, 通过模型评价指标评估剔除异常样本后建立的模型性能, 从而选择适合的波长或等分区间, 以确保模型在未知数据集上的预测能力和泛化能力达到最佳, 正态分布筛选法算法流程图如图2所示。

	Figure Option View Download New Window
	图2 正态分布筛选法流程图Fig.2 Normal distribution screening method flowchart

1.5 光谱数据预处理

在进行近红外光谱数据分析时, 预处理是一个不可或缺的环节, 其可以显著减少由于环境、仪器误差或样品不均一性带来的干扰, 从而提升后续建模的准确性和可靠性^{[12, 13, 14]}。在去除异常光谱样本后, 将样本集按照4∶ 1的比例随机划分为校正集和预测集, 随后采用四种预处理方法进行测试对比, 分别是多元散射校正(multiplicative scatter correction, MSC)、 Savitzky-Golay一阶求导、 SG平滑(savitzky-golay, SG)和标准正态变换(standard normal variate, SNV)。

1.6 光谱稳定性评价指标和模型评价指标

采用The Unscramber X 10.4软件进行光谱预处理和建立模型。剔除异常光谱和划分数据集后, 对光谱进行预处理, 接着用(partial least-square regression, PLSR)进行建模, 根据相对标准偏差(relative standard deviation, RSD), 以及校正集相关系数( $R_{c}^{2}$ ), 校正集均方根误差(root mean square error of cross validation, RMSECV), 预测集相关系数( $R_{p}^{2}$ ), 预测集均方根误差(root mean square error of prediction, RMSEP)和相对分析误差(relative percent deviation, RPD)这几个指标对不同的剔除策略进行比较和评估, 确定最佳异常样本剔除方法^[15]。

(1)相对标准偏差(RSD)

相对标准偏差可以衡量一组数据波动的相对大小, 相对标准偏差的值越小, 数据波动越小。

(2)校正集均方根误差(RMSECV)^[16]

RMSECV是指交叉验证中的均方根误差, 常用来衡量模型在交叉验证过程中预测值与实际参考值之间的误差大小, RMSECV的值越接近0, 说明模型的预测误差越小, 模型的性能越好。

(3)预测集均方根误差(RMSEP)

RMSEP是指预测均方根误差, 用来评估模型预测值与实际值之间的差异, 衡量了模型在新数据上的预测准确性, 越接近0的RMSEP值表示模型预测越准确。

(4)校正集相关系数( $R_{c}^{2}$ )

表征了校正集样本含量实际值与预测值之间的线性相关程度, 其取值范围为0到1。 $R_{c}^{2}$ 值越接近1, 表示模型能够更准确地预测校正集样本的含量真实值, 模型对数据的拟合程度越高。

(5)预测集相关系数( $R_{p}^{2}$ )

计算原理与 $R_{c}^{2}$ 一致, $R_{p}^{2}$ 主要用于评估模型在预测阶段的表现, 衡量了预测集样本含量实际值与模型预测值之间的线性关联程度, 其取值范围同样为0到1。当 $R_{p}^{2}$ 值接近1时, 表明模型能够较准确地预测未知数据集中的样本含量实际值。

(6)相对分析误差(RPD)^[17]

相对分析误差通过标准差与均方根误差的比值来计算, 与 $R_{p}^{2}$ 效果一样, 都表现模型的预测能力, RPD值的高低直接反映了模型在预测阶段的性能优劣, 即在未知数据集上的预测精度。当RPD值越高时, 说明模型具有更好的预测能力和数据拟合度。

2 实验与结果讨论

2.1 材料

采用天津聚恒达化工有限公司生产的无水葡萄糖粉末, 所有无水葡萄糖粉末样品均采用瓶装密封进行保存, 存放在25 ℃的干燥箱中, 以防止受潮和被污染; 配置葡萄糖溶液时采用去离子水, 所用去离子水pH范围在5.0~7.5, 吸光度小于0.001 AU, 可为采集近红外光谱数据提供一个稳定且低背景噪音的环境。

2.2 实验设备

葡萄糖溶液浓度近红外在线检测系统框架如图3所示, 包括反应釜、补料瓶、搅拌机、蠕动泵、光谱仪、探头、光源、光纤、计算机。

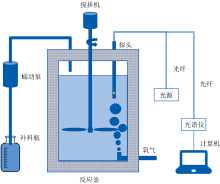	Figure Option View Download New Window
	图3 葡萄糖溶液浓度近红外在线检测系统框架Fig.3 Schematic diagram of on-line NIR detection system for glucose solution concentration

采用了海洋光学生产的NIRQUEST+1.7光纤光谱仪开展实验。光谱仪波长范围为900~1 700 nm, 由InGaAs线型传感器加上32 bit RISC微控制器组成, 采用光栅分光, 拥有精简架构及优化之光谱分析核心, 专用于检测近红外光谱, 其波长重现性为± 0.2 nm(对1 331.321波长采用海洋光学AR-2氩灯连续100次测量), 波长准确度为± 1 nm, 在解析度和波长漂移方面, 特别是在面对不同环境条件, 如温度变化、湿度波动、物体撞击、机械震动时, 波长准确度会在± 1.5 nm之内, 温度稳定性在0.2 nm· ℃^-1以内。光谱仪波长间隔约为3.22 nm, 单次数据采集时间通常约为2 s, 可以充分满足大部分应用场景的检测需求。

蠕动泵采用南京润泽流体生产的LM60智能灌装型蠕动泵, 可通过RS232/RS485通信调节速度和转向, 转速分辨率可达到± 0.1 RPM。为了验证蠕动泵的加料精度, 开展了单次转动加料重量的重复性测试。对其添加葡萄糖溶液重复性测试如表1所示。

表1 蠕动泵添加葡萄糖溶液重复性测试 Table 1 Repeatability test of peristaltic pump after adding glucose solution

从表1中数据分析得出, 蠕动泵单次葡萄糖溶液添加量最大值为2.062 8 g, 最小值为2.002 7 g, 最大差值为0.060 1 g, 平均值为2.043 7 g, 标准差为0.013 67 g。在后续建模实验中, 选取了平均值2.043 7 g作为单次所加入的葡萄糖溶液的重量。实际的加入量会在此平均值上下波动, 但是整个建模实验中大约加入了超过250次样品, 因此通过多次连续加料会在一定程度上消除单次加入量波动产生的误差。

该系统的主要功能可以分为三部分: 第一部分是反应釜中持续通入氧气使得反应釜中产生气泡, 造成部分光谱异常。第二部分是计算机利用串行通信接口对光谱仪发送控制指令, 定时采集并保存光谱数据, 确保实时监测反应釜中葡萄糖溶液的浓度变化。第三部分是计算机通过RS485串口通信控制蠕动泵的运转, 同时计算和记录反应釜中葡萄糖的实时浓度。蠕动泵通过硅胶管从预先配制的10%质量分数葡萄糖溶液补料瓶中抽取葡萄糖溶液, 并以精确的速率加入到反应釜中, 每30 s转动一圈, 每一次加入约2 g溶液, 确保反应釜中葡萄糖浓度的精确控制。

2.3 化学值测定

实验开始前, 所有的无水葡萄糖粉末样品都是在25 ℃的室温及干燥箱内密封保存。实验时, 首先将试纸平整地放在电子称上, 然后用药勺加葡萄糖至60 g。接下来, 在反应釜和补料瓶中各加入600和540 mL水, 并将准备好的60 g葡萄糖溶解在补料瓶中, 同时使用玻璃棒进行充分搅拌, 确保葡萄糖粉末充分溶解, 配制出质量分数为10%的葡萄糖溶液。计算机通过RS485串口通信精确控制蠕动泵的操作, 每隔30 s, 蠕动泵从补料瓶中抽取约2 g葡萄糖溶液, 精确地加入到反应釜中。同时, 计算机即时计算并记录每次加料后反应釜中的葡萄糖溶液浓度, 并将这些数据集保存在Excel文档中进行后续分析和处理。

2.4 近红外光谱数据采集

实验开始前, 将近红外探头和蠕动泵上的硅胶管伸入反应釜葡萄糖溶液中。采集光谱时, 采用漫反射模式进行光谱的采集, 光谱波长范围为900~1 700 nm, 共计248波长。对葡萄糖溶液进行3次扫描, 以确保采集到的光谱数据的稳定性, 然后导出相应的平均光谱数据, 将光谱与化学值按照时间一一对应, 保存至excel。

2.5 原始光谱分析

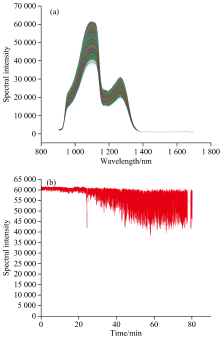
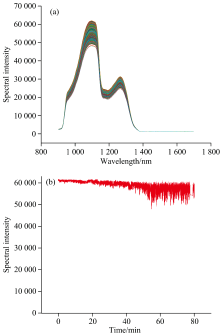
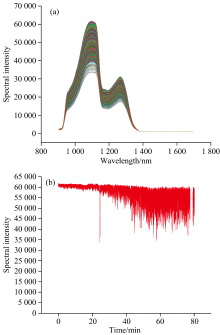
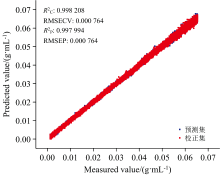
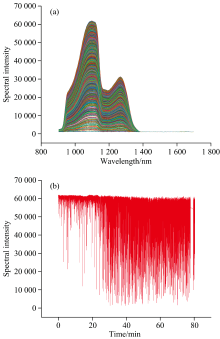采集的25 000条葡萄糖溶液反射光谱数据如图4(a)和 (b)所示, 受到气泡影响, 光谱峰值出现了较大的上下波动, 相对标准偏差RSD为15.88%。 PLSR模型预测结果如图5所示, 其校正集相关系数 $R_{c}^{2}$ 为0.955 465, 校正集均方根误差RMSECV为0.004 047, 预测集相关系数 $R_{p}^{2}$ 为0.954 855, 预测集均方根误差RMSEP为0.003 631, 误差较大, 预测效果不太理想。这表明部分异常光谱数据的存在可能影响了葡萄糖溶液光谱建模的准确性和可靠性。为了改善模型的预测效果, 需要减少光谱的波动, 对异常光谱进行剔除。

	Figure Option View Download New Window
	图4 (a)葡萄糖溶液近红外反射光谱; (b)葡萄糖溶液近红外反射光谱峰值变化Fig.4 (a) Near-infrared reflectance spectra of glucose solutions; (b) Change of peak intensity in near-infrared reflectance spectra of glucose solutions

	Figure Option View Download New Window
	图5 葡萄糖溶液近红外反射光谱建立的模型和葡萄糖溶液浓度预测散点图Fig.5 Scatter plot of model results versus measured glucose solution concentration

2.6 光谱预处理方法的选择

在进行近红外光谱建模的过程中, 要确保所建模型的准确性和可靠性, 关键在于尽量减少光谱数据中的噪声干扰^{[18, 19]}。为提高葡萄糖溶液光谱稳定性, 本研究针对葡萄糖溶液光谱稳定性进行了多种预处理方法的测试, 包括平滑、基线校正、标准正态变换(SNV), 多元散射校正(MSC)等预处理方法, 并按照4∶ 1的比例随机划分为校正集和预测集, 结合PLSR建模, 结果如表2所示。

表2 不同预处理方法对建模结果的影响 Table 2 The effect of different preprocessing methods on modeling results

预处理	校正集		预测集
预处理	RMSECV	$R_{c}^{2}$	RMSEP	$R_{p}^{2}$
原始光谱	0.004 047	0.955 465	0.003 631	0.954 855
MSC	0.001 245	0.994 780	0.001 414	0.993 153
Savitzky-Golay一阶求导	0.002 502	0.978 931	0.002 521	0.978 228
Savitzky-Golay平滑	0.003 787	0.951 723	0.003 781	0.951 046
SNV	0.001 217	0.995 009	0.001 385	0.993 427

表2 不同预处理方法对建模结果的影响 Table 2 The effect of different preprocessing methods on modeling results

除了平滑处理外, MSC、 SNV和基线校正都能够改善基于原始光谱数据构建的模型的性能, 其中以SNV对模型性能提升为最佳, 如图6所示, 使用SNV预处理后, 其校正集相关系数 $R_{c}^{2}$ 为0.995 009, 校正集均方根误差RMSECV为0.001 217, 比较原始光谱 $R_{c}^{2}$ 提升了0.039 544, RMSECV降低了0.002 83; 在预测集上, SNV预处理同样改善了预测能力, 预测集相关系数 $R_{p}^{2}$ 为0.993 427, 预测集均方根误差RMSEP为0.001 385, 比较原始光谱 $R_{p}^{2}$ 提升了0.038 572, RMSEP降低了0.002 246。

	Figure Option View Download New Window
	图6 SNV预处理后葡萄糖溶液近红外反射光谱建立的模型和葡萄糖溶液浓度预测散点图Fig.6 Scatter plot for model pretreated with SNV

2.7 光谱异常值识别方法对比与分析

对于PCA马氏距离法, 设定几个不同的百分位阈值D, 即95%, 90%, 85%, 80%, 75%, 70%, 对光谱数据进行筛选后, 将马氏距离超过每个阈值的样本标记为异常并剔除。接着, 针对剔除异常样本后的数据集再一次进行PLSR建模分析, 详细结果如表3所示。

表3 不同百分位阈值的剔除样品数及PLSR建模效果 Table 3 The number of samples removed by using different percentile thresholds and the modeling effect of PLSR

百分位阈值	剔除异常样品数	RSD	校正集		预测集
百分位阈值	剔除异常样品数	RSD	RMSECV	$R_{c}^{2}$	RMSEP	$R_{p}^{2}$
95%	1 237	10.51%	0.000 839	0.997 838	0.000 821	0.997 660
90%	2 459	8.27%	0.000 784	0.998 122	0.000 785	0.997 846
85%	3 695	7.16%	0.000 764	0.998 208	0.000 764	0.997 994
80%	4 918	7.00%	0.000 767	0.998 196	0.000 758	0.998 003
75%	6 154	6.93%	0.000 770	0.998 164	0.000 757	0.998 068
70%	7 376	6.92%	0.000 774	0.998 166	0.000 771	0.997 955

表3 不同百分位阈值的剔除样品数及PLSR建模效果 Table 3 The number of samples removed by using different percentile thresholds and the modeling effect of PLSR

分析显示, 当百分位阈值为95%和90%时, 模型的精度和预测能力较差; 进一步减小百分位阈值使得模型精度和预测能力提高, 当百分位阈值为85%时, 如图7(a)和(b)所示, 剔除异常光谱后, 光谱强度最大值的相对标准偏差RSD相比原始光谱降低8.72%, 光谱波动性下降, 模型精度和预测能力达到最优, 该百分位阈值下校正集 $R_{c}^{2}$ 为0.998 208, 比较剔除前提升0.003 199, 校正集RMSECV为0.000 764, 比较剔除前降低0.000 453, 预测集 $R_{p}^{2}$ 为0.997 994, 比较剔除前提升了0.004 567, RMSEP为0.000 764, 比较剔除前降低0.000 621, 如图8所示。

	Figure Option View Download New Window
	图7 (a)PCA马氏距离法筛选后的葡萄糖溶液反射光谱; (b)PCA马氏距离法筛选后的葡萄糖溶液反射光谱峰值变化Fig.7 (a) Reflectance spectra of glucose solutions screened by PCA Mahalanobis Distance Method; (b) Peak intensity of reflectance spectra of glucose solutions screened by PCA Mahalanobis Distance Method

	Figure Option View Download New Window
	图8 PCA马氏距离法剔除异常样本后建立的模型和葡萄糖浓度预测散点图Fig.8 Scatter plot of modeling results after elimination of outlier samples by the PCA Mahalanobis Distance Method

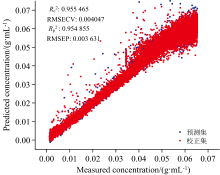
采用欧式距离剔除异常样本, 设定阈值为2σ , 剔除后的光谱如图9(a)和(b)所示, 光谱强度最大值的相对标准偏差RSD为3.88%, 比原始光谱降低了12%, 提高了光谱的稳定性。接着, 对剔除异常值后的样品集采用PLSR建模分析, 校正集 $R_{c}^{2}$ 为0.998 628, 比较剔除前提升了0.003 619, 校正集RMSECV为0.000 652, 比较剔除前降低了0.000 565, 预测集 $R_{p}^{2}$ 为0.998 628, 比较剔除前提升了0.005 201, 预测集RMSEP为0.000 655, 比较剔除前降低了0.000 73, 如图10所示。

Figure Option
View Download New Window

图9 (a)欧氏距离剔除异常光谱样本后的葡萄糖溶液反射光谱; (b)欧氏距离法剔除异常光谱样本后的葡萄糖溶液反射光谱峰值变化Fig.9 (a) Reflectance spectra of glucose solutions after anomalous samples rejected by Euclidean distance; (b) Changes of peak intensity of reflectance spectra after removal of anomalous spectral samples by the Euclidean distance method

	Figure Option View Download New Window
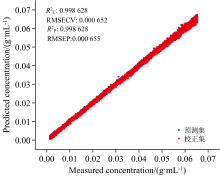	图10 欧式距离法剔除异常光谱样本后建立的葡萄糖溶液浓度模型和葡萄糖溶液浓度预测散点图Fig.10 Scatter plot of modeling results after excluding anomalous spectral samples by Euclidean distance method

采用孤立森林剔除异常光谱后的光谱如图11(a)和(b)所示, 光谱峰值的相对标准偏差RSD为7.18%, 相比原始光谱减少了8.7%, 光谱波动范围变小。然后, 采用PLSR对剔除异常样本后的光谱样本进一步建模分析。如图12所示, 校正集 $R_{c}^{2}$ 为0.998 255, 比较剔除前提升了0.003 246, 校正集RMSECV为0.000 739, 比较剔除前降低了0.000 478, 预测集 $R_{p}^{2}$ 为0.998 132, 比较剔除前提升了0.004 705, 预测集RMSEP为0.000 740, 比较剔除前降低了0.000 645。

Figure Option
View Download New Window

图11 (a)孤立森林法剔除异常光谱样本后的葡萄糖溶液反射光谱; (b)孤立森林法剔除异常光谱后的葡萄糖溶液反射光谱峰值变化Fig.11 (a) Reflectance spectra of glucose solutions after removal of anomalous spectral samples by the isolated forest method; (b) Changes of peak intensity of reflectance spectra after removal of anomalous spectra by the isolated forest method

	Figure Option View Download New Window
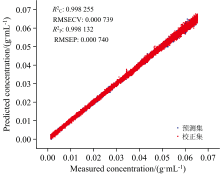	图12 孤立森林法剔除异常光谱样本后建立的模型和葡萄糖浓度预测散点图Fig.12 Scatter plot of modeling results after removing anomalous spectral samples by the isolated forest method

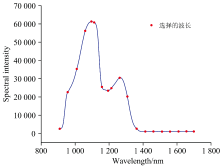
对于正态分布筛选法, 为研究正态分布筛选方法在葡萄糖溶液反射光谱不同波长的使用效果, 从248个波长中等距取出16个波长, 再加上两个波峰以及一个波谷对应的波长, 一共19个波长, 波长位置如图13所示。

	Figure Option View Download New Window
	图13 从248个波长中取出的19个波长Fig.13 Distribution of 19 wavelengths extracted from 248 wavelengths

分别对这19个波长使用正态分布筛选法, 随后进行PLSR建模分析, 对比建模结果, 选择出正态分布筛选方法效果最佳的波长, 结果如表4和图14、图15所示。

表4 19个波长点使用正态分布筛选法后的PLSR建模效果对比 Table 4 Comparison of PLSR modeling effects for 19 wavelengths using normal distribution screening

波长	$R_{c}^{2}$	RMSECV	$R_{p}^{2}$	RMSEP
909.36	0.998 613	0.000 660	0.998 517	0.000 632
956.26	0.998 615	0.000 654	0.998 610	0.000 618
1 009.59	0.998 629	0.000 655	0.998 511	0.000 637
1 059.32	0.998 625	0.000 657	0.998 545	0.000 634
1 095.63	0.998 659	0.000 657	0.998 596	0.000 621
1 112.09	0.998 617	0.000 655	0.998 585	0.000 624
1 158.03	0.998 634	0.000 657	0.998 427	0.000 645
1 193.97	0.998 616	0.000 656	0.998 514	0.000 636
1 213.52	0.998 671	0.000 655	0.998 556	0.000 630
1 262.22	0.998 605	0.000 660	0.998 531	0.000 634
1 307.45	0.998 637	0.000 659	0.998 623	0.000 621
1 362.08	0.998 615	0.000 662	0.998 575	0.000 627
1 413.22	0.998 174	0.000 770	0.998 101	0.000 752
1 460.92	0.998 225	0.000 778	0.998 077	0.000 764
1 511.53	0.998 220	0.000 779	0.998 133	0.000 766
1 558.73	0.998 136	0.000 799	0.998 180	0.000 754
1 608.82	0.998 233	0.000 761	0.998 154	0.000 738
1 655.54	0.998 264	0.000 731	0.998 185	0.000 715
1 698.93	0.998 132	0.000 786	0.998 076	0.000 762

表4 19个波长点使用正态分布筛选法后的PLSR建模效果对比 Table 4 Comparison of PLSR modeling effects for 19 wavelengths using normal distribution screening

	Figure Option View Download New Window
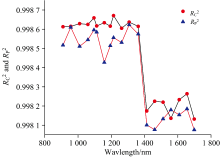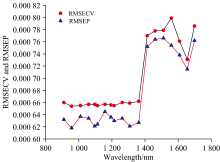	图14 19个波长经过正态分布筛选法处理后的PLSR建模效果对比( $R_{c}^{2}$ 和 $R_{p}^{2}$ )Fig.14 Comparison of PLSR modeling results using 19 wavelengths treated by normal distribution screening method ( $R_{c}^{2}$ and $R_{p}^{2}$ )

	Figure Option View Download New Window
	图15 19个波长点经过正态分布筛选法处理后的PLSR建模效果对比(RMSECV和RMSEP)Fig.15 Comparison of PLSR modeling effects of 19 wavelengths treated with normal distribution screening method (RMSECV and RMSEP)

从表4和图14, 图15可以看出, 对葡萄糖溶液反射光谱900~1 400 nm波段使用正态分布筛选法后, 得到的葡萄糖溶液浓度模型的校正集相关系数 $R_{c}^{2}$ 和预测集相关系数 $R_{p}^{2}$ 均高于1 400~1 700 nm波段, 校正集均方根误差RMSECV和预测集均方根误差RMSEP也均低于1 400~1 700 nm波段; 900~1 400 nm波段中的各波长使用正态分布筛选法后, 建立的模型效果差距不大, 故选用其中建模效果较好的光谱峰值波长1 095.63 nm进行光谱筛选。

为研究正态分布筛选法在不同区间数量下剔除葡萄糖溶液异常光谱的效果, 分别等距划分5, 10, 15, 20个区间, 找到波长点1 095.63 nm下光谱强度出现频率最高的区间, 保留其中的光谱强度对应的光谱, 其他区间的光谱剔除, 并对保留下来的光谱进行PLSR建模分析, 结果如表5所示。

表5 不同划分区间数量的PLSR建模效果 Table 5 PLSR modeling effects for different numbers of division intervals

序号	划分区间数量	剔除样品数	RSD	校正集		预测集
序号	划分区间数量	剔除样品数	RSD	RMSECV	$R_{c}^{2}$	RMSEP	$R_{p}^{2}$
1	5	4 580	4.71%	0.000 698	0.998 439	0.000 688	0.998 396
2	10	10 142	2.75%	0.000 645	0.998 641	0.000 636	0.998 628
3	15	12 070	2.51%	0.000 634	0.998 618	0.000 627	0.998 596
4	20	14 188	2.47%	0.000 632	0.998 625	0.000 622	0.998 601

表5 不同划分区间数量的PLSR建模效果 Table 5 PLSR modeling effects for different numbers of division intervals

分析表5可以发现, 当划分区间为10的时候, 模型的精度和预测能力达到最优, 如果继续细分区间, 可能会剔除部分有用的光谱信息, 导致预测集 $R_{p}^{2}$ 降低。

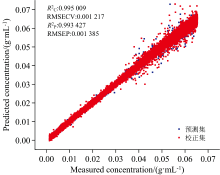
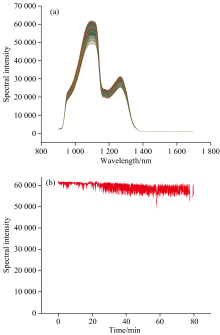
采用划分区间为10的正态分布筛选法剔除异常光谱后, 如图16(a)和(b)所示, 光谱峰值的相对标准偏差RSD为2.75%, 相比原始光谱减少了13.13%, 正态分布筛选法能够有效降低光谱的波动。随后, 用PLSR重新建立了葡萄糖溶液浓度模型, 如图17所示。校正集 $R_{c}^{2}$ 为0.998 641, 比较剔除前提升了0.003 632, 校正集RMSECV为0.000 645, 比较剔除前降低了0.000 572, 预测集 $R_{p}^{2}$ 为0.998 628, 比较剔除前提升了0.005 201, 预测集RMSEP为0.000 636, 比较剔除前降低了0.000 749。

Figure Option
View Download New Window

图16 (a)正态分布筛选法剔除异常光谱样本后的葡萄糖溶液反射光谱; (b)正态分布筛选法剔除异常光谱样本后的葡萄糖溶液反射光谱峰值变化Fig.16 (a) Reflectance spectra of glucose solutions after removal of anomalous spectral samples by the normal distribution screening method; (b) Changes of peak intensity of reflectance spectra after removal of anomalous spectral samples by the normal distribution screening method

	Figure Option View Download New Window
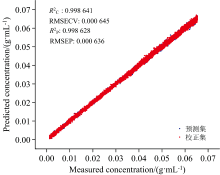	图17 正态分布筛选法剔除异常光谱样本后建立的葡萄糖溶液浓度模型和预测散点图Fig.17 Scatter plot of modeling results after removal of anomalous spectral samples by the normal distribution screening method

表6详细展示了多种异常样本剔除方法在剔除异常样本之后, 对光谱峰值相对标准偏差的影响, 以及对模型性能的提升效果。分析表中数据可以发现, 在尝试使用几种方法剔除异常样本后, 得到的模型均比未进行剔除的更好。说明四种不同的异常样本剔除方法均能有效减少近红外光谱数据的波动性, 增强光谱的整体稳定性, 并且提高建模的准确度, 且特别是在采用正态分布筛选法去除异常样本的情况下, 光谱数据波动性的降低最为显著, 建立的PLSR模型在预测性能和稳定性方面提升更多。

表6 基于不同异常样本剔除方法的葡萄糖溶液浓度建模及预测结果 Table 6 Modeling and prediction results of models for glucose solution concentration based on different abnormal sample elimination methods

序号	选择方法	RSD	RMSECV	$R_{c}^{2}$	RMSEP	$R_{p}^{2}$	RPD
1	不剔除异常样本	15.88%	0.001 217	0.995 009	0.001 385	0.993 427	10.021 5
2	马氏距离	7.16%	0.000 764	0.998 208	0.000 764	0.997 994	15.791 7
3	欧氏距离	3.88%	0.000 679	0.998 628	0.000 655	0.998 628	19.089 6
4	孤立森林	7.18%	0.000 755	0.998 255	0.000 740	0.998 132	16.368 1
5	正态分布筛选法	2.75%	0.000 645	0.998 641	0.000 636	0.998 628	19.096 6

3 结论

为提高近红外光谱检测分析发酵液中成分浓度的准确性和稳定性, 在建立近红外在线检测模型前和预测前, 应首先剔除受到气泡影响的近红外光谱。基于近红外光谱在某一波长的光谱强度近似符合正态分布的特性, 提出了正态分布筛选方法, 可用于剔除近红外在线监测中气泡引起的异常光谱, 降低光谱的波动。

为了深入探究正态分布筛选方法在剔除异常样本的应用效果, 将该算法运用于剔除葡萄糖溶液近红外光谱中的异常样本, 并构建了近红外定量分析模型。通过对多种不同的异常样本剔除方法进行对比实验, 结果表明正态分布光谱筛选方法在剔除近红外光谱中的异常样本方面表现出色, 能够显著降低光谱数据的波动性, 增强光谱数据的稳定性。由此构建的预测模型, 其稳健性强, 预测结果具有较高的准确性。

然而, 正态分布筛选方法也存在一定的局限性。例如, 在实际应用中, 需要通过多次建模验证来确定最佳的保留区间数量, 以达到最优的剔除效果。针对这一问题, 下一步工作可以考虑以下三个方向: 一是进一步改进算法, 提高其自动适应能力, 使其能够更加智能地确定最佳保留区间数量; 二是结合其他数据处理技术, 如孤立森林、局部异常因子等机器学习方法, 以提高筛选方法的准确性和稳定性; 三是开展更多的实际应用场景研究, 以验证和优化正态分布筛选方法在不同领域的适用性。

参考文献

文献列表

[1]	CHU Xiao-li, SHI Yun-ying, CHEN Pu, et al(褚小立, 史云颖, 陈瀑, 等). Journal of Instrumental Analysis(分析测试学报), 2019, 38(5): 603. [本文引用:1]
[2]	LONG Ruo-lan, FENG Dan, LUO Xi, et al(龙若兰, 冯丹, 罗西, 等). Journal of Instrumental Analysis(分析测试学报), 2023, 42(8): 920. [本文引用:1]
[3]	SHI Lu-zhen, ZHANG Jing-chuan, WANG Yan-qun, et al(石鲁珍, 张景川, 王彦群, 等). Journal of Chinese Agricultural Mechanization(中国农机化学报), 2016, 37(6): 99. [本文引用:1]
[4]	Zhang L X, Li P W, Mao J, et al. Journal of Computational Chemistry, 2015, 36: 1902. [本文引用:1]
[5]	Chen W C, Du Y P, Zhang F Y, et al. Journal of Chemometrics, 2017, 32(11): e2933. [本文引用:1]
[6]	WANG Ya-dong, JIA Jun-wei, TAN Wei-jun, et al(王亚栋, 贾俊伟, 谭韦君, 等). Journal of Instrumental Analysis(分析测试学报), 2024, 43(4): 607. [本文引用:1]
[7]	LUO Lin, TUO Xian-guo, ZHANG Gui-yu, et al(罗林, 庹先国, 张贵宇, 等). Journal of Food Safety and Quality(食品安全质量检测学报), 2022, 13(9): 3017. [本文引用:2]
[8]	CHEN Bin, ZOU Xian-yong, ZHU Wen-jing(陈斌, 邹贤勇, 朱文静). Journal of Jiangsu University (Natural Science Edition)[江苏大学学报(自然科学版)], 2008, 29(4): 277. [本文引用:1]
[9]	WANG Hao, WANG Peng, YU Jia-hang, et al(王浩, 王鹏, 余嘉航, 等). Science and Technology of Food Industry(食品工业科技), 2021, 42(17): 235. [本文引用:1]
[10]	HUANG Yuan-cheng, XUE Yuan-yuan, LI Peng-fei(黄远程, 薛园园, 李朋飞). Acta Geodaetica et Cartographica Sinica(测绘学报), 2021, 50(3): 416. [本文引用:1]
[11]	XIONG Kun, DING Qiang, ZHU Hong-mei(熊坤, 丁强, 祝红梅). Computer Application and Software(计算机应用与软件), 2023, 40(1): 84. [本文引用:1]
[12]	QIN Wen-hu, DONG Kai-yue, DENG Zhi-chao(秦文虎, 董凯月, 邓志超). Soils(土壤), 2023, 55(6): 1347. [本文引用:1]
[13]	LI Chun-yan, YE Li-ming, XUE Jin-tao(李春燕, 叶利明, 薛金涛). Physical Testing and Chemical Analysis (Part B: Chemical Analysis)[理化检验(化学分册)], 2023, 59(12): 1407. [本文引用:1]
[14]	QU Qiong, HAN Li-zhu, ZHAO Xiao-mei, et al(屈琼, 韩立柱, 赵小梅, 等). Chinese Traditional and Herbal Drugs(中草药), 2023, 54(21): 7017. [本文引用:1]
[15]	XU Hong-fa, LIU Zheng-hui, ZHANG Hong-mei, et al(徐宏发, 刘正辉, 张红梅, 等). Journal of Zhejiang University(Agriculture and Life Sciences)[浙江大学学报(农业与生命科学版)], 2024, 50(3): 393. [本文引用:1]
[16]	HAN Xiang, HE Xiao-gang, YU Jia-ping, et al(韩想, 贺小刚, 于佳萍, 等). Physical Testing and Chemical Analysis (Part B: Chemical Analysis)[理化检验(化学分册)], 2023, 59(7): 792. [本文引用:1]
[17]	ZHANG Xun, HUANG Xiao-xuan, YIN Jin-ke, et al(张勋, 黄晓萱, 殷金可, 等). Chinese Journal of Modern Applied Pharmacy(中国现代应用药学), 2023, 40(19): 2702. [本文引用:1]
[18]	SUN Tong, LI Han-lin, KONG Ling-fei, et al(孙通, 李翰林, 孔令飞, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2023, 39(24): 298. [本文引用:1]
[19]	WANG Qi, MA Hui-feng, CAI Jian-bo, et al(王启, 马辉峰, 蔡建波, 等). China Brewing(中国酿造), 2023, 42(12): 161. [本文引用:1]

2019

0.0

... 在发酵过程的监测与控制中, NIRS能够即时监测关键的工艺参数, 减少人力成本, 提高生产效率, 展现出其独特的优势^[1] ...

2023

0.0

... 龙若兰等采用马氏距离结合主成分分析对近红外光谱进行异常样本剔除^[2] ...

2016

0.0

... 石鲁珍等选取一阶导数前4个主成分的得分进行马氏距离计算, 将大于阈值的异常光谱样品剔除, 用剩下的样品建立模型, 预测精度相较于剔除前得到明显的改善^[3] ...

2015

0.0

... Zhang等基于正常样本建立的交互预测模型和疑似异常样本的独立验证, 提出了一种增强的蒙特卡罗界外样本识别方法^[4] ...

2017

0.0

... Chen等在模型集群分析算法的基础上提出了采样误差分布分析算法, 可用于异常样本的筛选^[5] ...

2024

0.0

... 法则对异常样本进行迭代剔除^[6] ...

2022

0.0

... 2%^[7] ...

... 欧式距离法剔除异常光谱具体步骤如下^[7]: ...

2008

0.0

... 420%^[8] ...

2021

0.0

... 马氏距离法是一种用来衡量点与分布之间距离的度量方法, 它考虑了数据分布的协方差, 使得不同维度上数值差异对距离的影响得到了合理调整^[9] ...

2021

0.0

... 3 孤立森林剔除异常光谱孤立森林算法的基本理念是异常数据偏离大部分数据, 往往在较少的分割操作之后就会被有效地孤立^[10] ...

2023

0.0

... 这样, 每一棵iTree都是孤立的, 并且具有不同的特征切割点, 用生成的孤立树来评估测试数据, 即计算异常分数s, 见式(1)^[11] ...

2023

0.0

... 5 光谱数据预处理在进行近红外光谱数据分析时, 预处理是一个不可或缺的环节, 其可以显著减少由于环境、仪器误差或样品不均一性带来的干扰, 从而提升后续建模的准确性和可靠性^[12,13,14] ...

2023

0.0

2023

0.0

2024

0.0

... 剔除异常光谱和划分数据集后, 对光谱进行预处理, 接着用(partial least-square regression, PLSR)进行建模, 根据相对标准偏差(relative standard deviation, RSD), 以及校正集相关系数( Rc2), 校正集均方根误差(root mean square error of cross validation, RMSECV), 预测集相关系数( Rp2), 预测集均方根误差(root mean square error of prediction, RMSEP)和相对分析误差(relative percent deviation, RPD)这几个指标对不同的剔除策略进行比较和评估, 确定最佳异常样本剔除方法^[15] ...

2023

0.0

... (2)校正集均方根误差(RMSECV)^[16] ...

2023

0.0

... (6)相对分析误差(RPD)^[17] ...

2023

0.0

... 6 光谱预处理方法的选择在进行近红外光谱建模的过程中, 要确保所建模型的准确性和可靠性, 关键在于尽量减少光谱数据中的噪声干扰^[18,19] ...

2023

0.0

... 6 光谱预处理方法的选择在进行近红外光谱建模的过程中, 要确保所建模型的准确性和可靠性, 关键在于尽量减少光谱数据中的噪声干扰^[18,19] ...