高温金属表面红外辐射偏振特性研究

引用本文

杨晨南, 付跃刚, 欧阳名钊, 原帅, 贺文俊, 赵宇森. 高温金属表面红外辐射偏振特性研究[J]. 光谱学与光谱分析, 2025,45(6): 1557-1565.
YANG Chen-nan, FU Yue-gang, OUYANG Ming-zhao, YUAN Shuai, HE Wen-jun, ZHAO Yu-sen. Polarization Characteristics of Infrared Radiation on High-Temperature Metal Surfaces[J]. Spectroscopy and Spectral Analysis, 2025,45(6): 1557-1565.
Doi:10.3964/j.issn.1000-0593(2025)06-1557-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

高温金属表面红外辐射偏振特性研究

杨晨南^1,², 付跃刚^1,^2,^*, 欧阳名钊^1,^2,^*, 原帅^1,², 贺文俊^1,², 赵宇森^1,²

1.长春理工大学光电测控与光信息传输技术教育部重点实验室, 吉林长春 130022

2.长春理工大学光电工程学院, 吉林长春 130022

*通讯作者 e-mail: fuyg@cust.edu.cn; oymz68@163.com

作者简介: 杨晨南, 2000年生,长春理工大学硕士研究生 e-mail: 1609785000@qq.com

收稿日期: 2024-08-21 修订日期: 2024-12-18

基金: 国家自然科学基金项目(61705018),吉林省教育厅科技基金项目(JJKH20210814KJ)资助

摘要

偏振特性是光场中除强度与光谱之外的又一维重要特性, 在目标识别、军事侦察和红外目标探测等领域展现出广阔的应用前景。航天发动机、高速飞行器等人造物体通常温度可以达到几百摄氏度, 因此具有高温自辐射特性。然而, 高温情况下目标的红外偏振特性研究却相对较少, 尤其是缺乏针对不同金属表面在较高温度下的偏振特性的深入探索。为了研究高温金属表面的辐射偏振特性, 采用基于微面元理论的双向反射分布函数模型, 结合镜面反射与漫反射特性, 系统性地建立了基于金属自发辐射能量的偏振双向反射分布函数与红外辐射偏振度的数学模型。通过推导与计算, 分析了不同表面粗糙度和温度条件下, 金属对红外辐射线偏振度的影响规律。仿真结果表明, 在相同温度下, 金属表面的粗糙度越大, 偏振度越低; 相反, 在相同粗糙度下, 随着温度的升高, 偏振度逐渐增加。同时利用LGC6122型长波红外相机与WP25M-IRC红外线栅偏振片, 对金属铁和45号钢进行了在8~14 μm波段内的目标自发辐射偏振热成像, 获取了150、 200、 250、 300、 400和500 ℃下的长波红外线偏振度数据。针对实验观测而言, 受普朗克黑体辐射定律影响, 金属表面温度与其光谱积分偏振度呈正相关状态, 温度越高, 光谱积分偏振度越大。同时随着观测角度的增加, 偏振度也逐渐增大, 在70°~80°范围内达到峰值。该研究成果旨在提升红外目标检测等应用中热成像和光学传感技术的精度和其可靠性, 并为未来进一步探索复杂环境下的红外探测技术提供参考。

关键词: 红外辐射偏振特性; 高温金属; 偏振度; 目标检测

中图分类号:O436.3 文献标志码:A

Polarization Characteristics of Infrared Radiation on High-Temperature Metal Surfaces

YANG Chen-nan^1,², FU Yue-gang^1,^2,^*, OUYANG Ming-zhao^1,^2,^*, YUAN Shuai^1,², HE Wen-jun^1,², ZHAO Yu-sen^1,²

1. Key Laboratory of Optoelectric Measurement and Optical Information Transmission Technology, Ministry of Education, Changchun University of Science and Technology, Changchun 130022, China

2. School of Optoelectronic Engineering, Changchun University of Science and Technology, Changchun 130022, China

*Corresponding authors

Abstract

Polarization is a crucial dimension in the light field, alongside intensity and spectrum, and holds significant promise in applications such as target recognition, military reconnaissance, and infrared target detection. Artificial objects, such as spacecraft engines and high-speed aircraft, typically reach temperatures of several hundred degrees Celsius, exhibiting high-temperature self-radiation characteristics. However, there has been relatively little research on the infrared polarization characteristics of targets at high temperatures, particularly concerning the polarization properties of different metal surfaces under elevated temperatures. To investigate the polarization characteristics of high-temperature metal surfaces, a bidirectional reflection distribution function model based on microplane theory was systematically developed. This model incorporates both specular and diffuse reflection characteristics, establishing a mathematical framework for the BRDF of metal spontaneous radiation energy and the degree of polarization of infrared radiation. Through derivation and calculation, the influence of various surface roughness and temperature conditions on the polarization degree of infrared radiation from metals was analyzed. Simulation results indicate that at the same temperature, higher surface roughness of the metal leads to a lower polarization degree. Conversely, under the same roughness, the polarization degree increases with rising temperature. In parallel, thermal imaging of spontaneous radiation polarization was performed using an LGC6122 long-wave infrared camera and a WP25M-IRC infrared gate polarizer. The targets studied were iron and 45 steel, within the 8~14 μm wavelength range, at temperatures of 150, 200, 250, 300, 400, and 500 ℃. Experimental observations revealed that, influenced by Planck's blackbody radiation law, the surface temperature of the metal is positively correlated with its spectral integral polarization degree: as the temperature increases, so does the spectral integral polarization degree. Additionally, the polarization degree gradually increases with the observation angle, peaking within the 70°to 80° range. The findings of this study aim to enhance the accuracy and reliability of thermal imaging and optical sensing technologies in infrared target detection and other related applications. Furthermore, they provide a reference for further exploration of infrared detection technologies in complex environments.

Keyword: Polarization characteristics of infrared radiation; High-temperature metal; Polarization degree; Target detection

文章图片

引言

近年来, 随着光电探测技术的不断进步, 红外成像技术作为一项重要的高新技术, 被广泛应用于军事^{[1, 2]}、安防^[3]、医学检测^{[4, 5]}、航空航天^[6]和目标探测^[7]等领域。红外偏振技术在反伪装识别方面已经开展了一些有价值的研究^[8]。

航天发动机、高速飞行器等人造物体通常温度可以达到几百摄氏度, 因此具有高温自辐射特性^[9]。然而, 高温下目标的红外偏振特性研究却相对较少, 尤其是针对不同金属在较高温度下的偏振特性缺乏深入探索。汪震等探讨了中温下铝面与钢制板材热红外偏振度与这些表面的粗糙度之间的关联, 得出的结论揭示了表面粗糙度降低会促使热红外偏振度提升的现象^[10]。徐文斌等在较低温度下, 对两类伪装目标进行了高光谱偏振成像实验, 研究结果显示, 温度改变越大, 偏振特性提升量越大^[11]。北京环境特性研究所实施了一系列高光谱偏振成像实验, 实验对象为在不同温度和不同观测角度下的涂漆和镀铝目标, 结果表明, 温度和观测角度对目标的偏振特性有较大影响, 目标表面的红外光谱偏振特性随辐射温度差值以及探测角度的差值增大而增大^[12]。 Jordan和Lewis通过实验分析了在10.6 μ m光谱处的不同粗糙度下铝板的红外偏振特性^[13]。金属材料在高温情况下偏振特性与常温情况下的并不相同, 这种偏振特性对红外成像系统的性能和目标探测能力有着重要的影响, 所以研究高温金属的偏振特性是一件有意义的工作。

本工作主要通过红外辐射偏振传输方程, 对与红外辐射偏振信息相关的温度、粗糙度、观测角度等参数的数学模型进行分析, 推导了目标表面温度以及观测角度对高温金属自发热辐射偏振度的影响; 通过实验获取高温金属的偏振特性。本研究结果对高温环境下红外目标的偏振识别技术发展具有重要意义。

1 理论基础

双向反射分布函数(bidirectional reflectance distribution function, BRDF)最早由Nicodemus在20世纪70年代定义^[14], 符号表示为f_BRDF

$f_{BRDF} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) = \frac{d L_{r} (θ_{r}, φ_{r}, λ)}{d E_{i} (θ_{i}, φ_{i}, λ)} (s r^{- 1})$ (1)

式(1)中, E_i为入射辐照度, L_r为反射辐亮度, θ 为天顶角, φ 为方位角。下标i表示入射方向, 下标r表示反射方向, λ 是波长。

BRDF描述了物体表面在不同入射角下、任意观测角度的反射特性, 是用于表征物体表面光反射行为的一个函数^[15]。在此, 微面元模型采用高斯分布来表述表面粗糙物体的微面元法线分布概率分布函数^[16]

$p (α) = \frac{1}{2 π σ^{2} co s^{3} (α)} \exp [\frac{- ta n^{2} (α)}{2 σ^{2}}]$ (2)

式(2)中, α 为宏观表面法线与微面元法线间的夹角, σ 为粗糙度常数。

1.1 基于微面元的双向反射分布函数

当目标表面粗糙, 而不是理想光滑情况时, 会发生遮蔽效应。随着目标表面粗糙度的增加, 阴影遮蔽效应的概率也会提高。因此, 在构建适用于粗糙目标表面的微面元BRDF模型时, 需要考虑遮蔽效应的作用。

带遮蔽函数的微面元BRDF模型的数学定义如式(3)

$f_{BRDF} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) = \frac{1}{2 π} \frac{1}{4 σ^{2}} \frac{1}{co s^{4} α} \cdot$

$\frac{\exp [- ta n^{2} (α \frac{)}{2} σ^{2}]}{\cos θ_{r} \cos θ_{i}} G (θ_{i}, θ_{r}, σ)$ (3)

式(3)中, G(θ _i, θ _r, σ )为遮蔽因子; θ _i和θ _r分别为入射光和反射光方向与宏观表面法线的夹角。

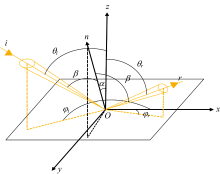
	Figure Option View Download New Window
	图1 BRDF的几何表示Fig.1 Geometric representation of BRDF

z轴表示宏观表面法线方向, n轴为微面法线方向, β 为入射光与微面法线的夹角, φ _i和φ _r分别为入射光和反射光的方位角。 θ _i、 φ _i、 θ _r、 φ _r、 α 、 β 各角间满足下列关系

$\cos (α) = \frac{\cos (θ_{i}) + \cos (θ_{r})}{2 \cos (β)}$ (4)

$\cos (2 β) = \cos (θ_{i}) \cos (θ_{r}) + \sin (θ_{i}) \sin (θ_{r}) \cos (φ_{r} - φ_{i})$ (5)

基于微面元的偏振BRDF坐标系由四个平面构成。 ioz平面由物体表面的入射和反射方向形成, ion平面由微面入射方向和法线方向形成, roz平面由物体表面的观测和法线方向形成的, ron平面是由微面观察方向和法线形成的。 η _i取决于ioz和ion两个平面之间的夹角, η _r取决于roz和ron两个平面之间的夹角。 η _i, η _r和θ _i, θ _r, β 满足如下关系

$\cos (η_{i}) = [(\cos θ_{i} + \cos θ_{r}) / (2 cosβ) - \cos θ_{i} cosβ \frac{]}{(} \sin θ_{i} sinβ)$ (6)

$\cos (η_{r}) = [(\cos θ_{i} + \cos θ_{r}) / (2 cosβ) - \cos θ_{r} cosβ \frac{]}{(} \sin θ_{r} sinβ)$ (7)

Jones与Muller部分矩阵元之间的关系^[17]如式(8)

$\{\begin{array}{l} M_{00} = \frac{1}{2} (| J_{ss} |^{2} + | J_{sp} |^{2} + | J_{ps} |^{2} + | J_{pp} |^{2}) \\ M_{10} = \frac{1}{2} (| J_{ss} |^{2} - | J_{sp} |^{2} + | J_{ps} |^{2} - | J_{pp} |^{2}) \\ M_{20} = \frac{1}{2} (J_{ss} J_{sp}^{*} + c.c. + J_{ps} J_{pp}^{*} + c.c.) \end{array}$ (8)

采用Muller矩阵来描述偏振态

$f_{BRDF} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) = \frac{1}{2 π} \frac{1}{4 σ^{2}} \frac{1}{co s^{4} α} \frac{\exp [- ta n^{2} (α \frac{)}{2} σ^{2}]}{\cos θ_{r} \cos θ_{i}} \cdot$

$G (θ_{i}, θ_{r}, σ) M_{jk} (θ_{i}, φ_{i}, θ_{r}, φ_{r})$ (9)

式(9)中, j=0, 1, 2, 3; k=0, 1, 2, 3; M_jk(θ _i, φ _i, θ _r, φ _r)为Muller矩阵元。

1.2 粗糙表面红外偏振特性建模

由微面元理论可以得知, 在金属表面所形成的微面元遵循菲涅尔反射定律, 即光进入到金属表面时, 和金属作用后会产生镜面反射和漫反射, 在分析高温金属表面偏振特性时, 这二部分的影响都应被考虑。表面反射系数随角度的变化可以被Minnaert模型很好的模拟出来, 故用该模型来表示漫反射部分的影响^[18]

$f_{d} = \frac{k_{d}}{π} (\cos θ_{i} \cos θ_{r})^{C} M_{jk}^{d}$ (10)

式(10)中, k_d为漫反射系数; C为范围为(-1, 0)的待定系数, $M_{jk}^{d}$ 为漫反射的Muller矩阵元, 其中除 $M_{00}^{d}$ =1, 其他元素均为0^[19]。

根据对金属表面粗糙度所产生的漫反射作用, 引入了镜面反射系数和漫反射系数, 从而构建了金属辐射表面的偏振BRDF模型

$F_{jk} = \frac{k_{s} \exp (\frac{- ta n^{2} α}{2 σ^{2}}) G (θ_{i}, θ_{r}, σ)}{8 π σ^{2} co s^{4} αcos θ_{i} \cos θ_{r}} M_{jk}^{s} +$

$\frac{k_{d}}{π} (\cos θ_{i} \cos θ_{r})^{C} M_{jk}^{d}$ (11)

式(11)中, k_s为镜面反射系数, $M_{jk}^{s}$ 为镜面反射的Muller矩阵元。

在本文中, k_s和k_d这两个未知参数由全积分散射(total integrated scattering, TIS)计算得出, TIS定义为散射反射能量P_d与总反射能量P_t之比。 1961年, Bennett和Porteus假设表面高度服从高斯分布, 推导出了两者之间的关系^[20]

$TIS = \frac{P_{d}}{P_{t}} = 1 - \exp [- (4 πσcos θ_{i} {/ λ)}^{2}]$ (12)

入射光入射到金属表面时, 会发生吸收、反射和透射作用, 根据能量守恒定律, 这三者的和为1。对于金属而言, 透射率τ =0, 因此

$α_{a} (λ, T) + ρ (λ, T) = 1$ (13)

式(13)中, α _a为金属的吸收率, ρ 为反射率, T为温度。根据基尔霍夫定律及发射率的定义, 在相同的温度下, 金属的光谱的发射率与吸收率相同, 因此金属的发射率可以表示为

$ε = α_{a} = 1 - ρ$ (14)

式(14)中, ε 表示金属的发射率, 发射率是依据物体本身的温度辐射出能量的能力, 发射率越高, 辐射能量越大。

对BRDF在半球内进行积分, 可以得到方向半球反射率, 将其推广到偏振形式, 可得方向半球的发射率ε _DE为

$ε_{DE} = 1 - ρ_{DHR} = 1 -$

$\int_{0}^{2} \int_{0}^{\frac{π}{2}} F (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \sin θ_{r} \cos θ_{r} d θ_{r} d φ_{r}$ (15)

式(15)中, ρ _DHR为方向半球反射率, 物体发射率ε _sur与理想黑体发射率ε _bb满足

$ε_{sur} = ε_{DE} ε_{bb}$ (16)

由于理想黑体无偏振特性, 所以其斯托克斯矢量ε _bb=[1 0 0 0]^T, 据此, 可以得到金属表面红外辐射定向发射率斯托克斯表达式为

$ε_{surf} = (\begin{array}{l} 1 - \underset{Ω_{r}}{\int \int} F_{00} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \cos θ_{r} d Ω_{r} \\ - \underset{Ω_{r}}{\int \int} F_{10} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \cos θ_{r} d Ω_{r} \\ - \underset{Ω_{r}}{\int \int} F_{20} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \cos θ_{r} d Ω_{r} \\ - \underset{Ω_{r}}{\int \int} F_{30} (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \cos θ_{r} d Ω_{r} \end{array})$ (17)

物体辐射包含了反射辐射和自发辐射两个部分, 因此入射到红外偏振相机前的斯托克斯矢量S_in为

$S_{in} = S_{r} + S_{e} =$

$\underset{Ω_{r}}{\int \int} F (θ_{i}, φ_{i}, θ_{r}, φ_{r}, λ) \cos θ_{r} d Ω_{r} S^{i} + ε_{surf} I_{obj}$ (18)

式(18)中, S_r为反射辐射, S_e为自发辐射, I_obj为目标辐射强度。在红外偏振成像系统中, 入射Stokes矢量为Sⁱ=[I_bg 0 0 0]。则入射到相机镜头前的Stokes矢量为

$S_{in} = (\begin{array}{l} I \\ Q \\ U \\ V \end{array}) = (\begin{array}{l} I_{obj} - \underset{Ω_{r}}{\int \int} F_{00} \cos θ_{r} d Ω_{r} (I_{bg} - I_{obj}) \\ - \underset{Ω_{r}}{\int \int} F_{10} \cos θ_{r} d Ω_{r} (I_{bg} - I_{obj}) \\ - \underset{Ω_{r}}{\int \int} F_{20} \cos θ_{r} d Ω_{r} (I_{bg} - I_{obj}) \\ - \underset{Ω_{r}}{\int \int} F_{30} \cos θ_{r} d Ω_{r} (I_{bg} - I_{obj}) \end{array})$ (19)

式(19)中, I_bg表示背景的辐射强度。由Stokes原理可知, 圆偏振分量通常较小, 可以忽略不计^[21], 得到

目标的辐射线偏振度(degree of linear polarization, DOLP)可以表示为

$DOLP = \frac{\sqrt[]{Q^{2} + U^{2}}}{I}$ (21)

2 仿真分析

利用偏振双向反射分布函数建立微面元, 对不同温度和不同观测角度下的金属进行偏振度数值的仿真。本工作数值计算的波长为10 μ m的长波红外谱段, 选择的材料为金属铁和45号钢, 金属铁的粗糙度分别取0.61、 0.69及0.8 μ m, 其对应粗糙度的k_s依次为0.555 7、 0.471 5和0.364, k_d依次为0.444 3, 0.528 5和0.636, 复折射率取n=7.07, k=27.90。 45号钢的粗糙度分别取0.65、 0.73及0.8 μ m, 其对应粗糙度的k_s依次为0.513 2, 0.431 1和0.364, k_d依次为0.486 8, 0.568 9和0.636, 复折射率取n=5.23, k=24.64。分别对以上两种材质进行300、 400及500 ℃情况下的仿真。图2为金属铁在相同温度不同粗糙度下的仿真曲线。

	Figure Option View Download New Window
	图2 DT4C铁在不同粗糙度下的DOLP仿真结果 (a): 300 ℃; (b): 400 ℃; (c): 500 ℃Fig.2 DOLP simulation results of DT4C iron with different roughnesses (a): 300 ℃; (b): 400 ℃; (c): 500 ℃

根据图2分析知, 对于铁金属, 随着σ 的增大, 其红外线偏振度减小, 峰值处的线偏振度差值最大, 随着温度的增加, 其红外线偏振度的数值也会增大, 但在σ 较大的情况下, 偏振度随温度变化较小, σ 的数值越小, 温度对线偏振度的影响越大。

将仿真材料替换为45号钢并对该材料的粗糙度参数进行仿真, 得到如图3所示的结果。

	Figure Option View Download New Window
	图3 45号钢在不同粗糙度下的DOLP仿真结果 (a): 300 ℃; (b): 400 ℃; (c): 500 ℃Fig.3 DOLP simulation results of 45^# steel with different roughnesses (a): 300 ℃; (b): 400 ℃; (c): 500 ℃

与铁金属偏振度变化规律相同, 45号钢的偏振度随着观测角度的增加而增大, 偏振度峰值存在于70° ~80° 间, 红外偏振度随着σ 的增大而减小, 随着温度的增加而增大。接下来将粗糙度作为常量, 温度作为变量进行仿真, 其中铁的粗糙度为0.61 μ m, 钢的粗糙度为0.65 μ m, 如图4所示。

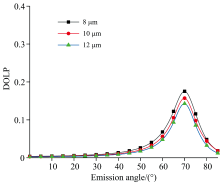
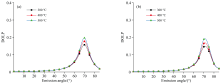	Figure Option View Download New Window
	图4 不同温度相同粗糙度的DOLP仿真结果 (a): DT4C铁; (b): 45号钢Fig.4 DOLP simulation results of DT4C iron and 45^# steel with same roughness at different temperatures (a): DT4C iron; (b): 45^# steel

在粗糙度保持不变的情况下, 随着温度的升高, 在70° 观测角处的偏振度峰值附近的数值有明显的上升, 两种金属线偏振度都随着观测角度的增加而增加, 在达到峰值后又急剧减少, 铁和45号钢在不同条件下的长波红外线偏振度峰值均保持在70° ~80° 范围内。同时, 45号钢和铁的线偏振度在小角度处变化不大, 在50° 时开始大幅度上升。

对两种金属在相同粗糙度0.61 μ m情况下的DOLP进行仿真, 仿真参数k_s为0.555 7, k_d为0.444 3, 仿真结果如图5所示。

	Figure Option View Download New Window
	图5 粗糙度为0.61 μ m的不同金属DOLP仿真结果 (a): 300 ℃; (b): 400 ℃; (c): 500 ℃Fig.5 DOLP simulation results of different metals with a roughness of 0.61 μ m (a): 300 ℃; (b): 400 ℃; (c): 500 ℃

由仿真结果可知, 两种金属在相同粗糙度0.61 μ m时, 45号钢的偏振度要比铁的偏振度稍大。

对不同波段处的铁金属线偏振度进行仿真, 图6显示了300 ℃时不同光谱谱段下金属铁的DOLP仿真结果, 结果表明, 随着波长的增加偏振度会有一定的降低。

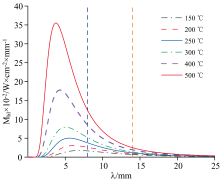
	Figure Option View Download New Window
	图6 300 ℃时不同波段铁金属的DOLP仿真结果Fig.6 DOLP simulation results of iron metals in different bands at 300 ℃

对于使用红外探测器的观测试验而言, 其观测积分能量的光谱区间相对固定, 由普朗克黑体辐射定律可知, 随着温度的升高, 黑体辐射峰值会往短波迁移, 同时, 在相同温度情况下波长较短处比波长较长处的黑体辐出射度高, 如图7所示。因此, 在探测器光谱探测范围内(8~14 μ m, 即图7中两竖直虚线区域内)随温度的升高, 黑体的辐出射度会有所增加, 温度越高, 辐出射度增加越大。同时根据图6的仿真结果可知, 高温时在其他条件相同下, 短波长偏振度比长波偏振度高。因此, 其在长波探测器探测谱段内的积分光谱偏振度会随高温温度的上升而变高。综合仿真数据可以得出结论, 两种材料的偏振度峰值均在70° ~80° 之间, 粗糙度越大, 偏振度越小; 当温度升高时, 随着温度的增加, 偏振度也随之增大。

	Figure Option View Download New Window
	图7 不同温度下黑体辐出射度与波长的关系Fig.7 Relationship between blackbody radiation emission and wavelength at different temperatures

3 红外金属偏振探测实验及数据处理

为了验证仿真金属目标温度与红外偏振特性关系的趋势结论, 实验室通过调节不同的温度, 开展了金属红外偏振探测实验研究。选用了铁和45号钢金属作为实验材料, 用LGC6122型长波红外相机以及WP25M-IRC红外线栅偏振片获取目标自发辐射热成像, 实验在暗室内进行, 室内温度为25 ℃。相机具体参数由表1给出; 偏振片消光最大可达到10 000∶ 1, 在长波范围内透射率大于75%, 工作波长为7~15 μ m。利用上位机对获取的数据进行处理, 相机在拍摄时储存的图片均为未经过非均匀校正处理的原始数据, 实验原理图如图8所示。

表1 长波红外相机具体参数 Table 1 Long wave infrared camera specific parameters

	Figure Option View Download New Window
	图8 实验装置搭建图Fig.8 Construction diagram of experimental device

实验过程中, 利用喷枪依次将样品加热, 使用红外线测温仪对金属样品表面温度进行测量, 当测得金属表面温度依次到达300、 400以及500 ℃并保持稳定后, 旋转偏振片, 获取0° 、 45° 、 90° 和135° 下的偏振角度图像, 融合采集不同观测角度下实验的热红外偏振图像。如图9— 图11为500 ℃时, 铁金属的5° 、 25° 和55° 观测角度的光强图与偏振度图, 以及不同温度下5° 观测角度偏振度图像。

	Figure Option View Download New Window
	图9 500 ℃ DT4C铁不同观测角度光强图像 (a): 5° ; (b): 25° ; (c): 55° Fig.9 Intensity images of 500 ℃ DT4C iron at different observation angles (a): 5° ; (b): 25° ; (c): 55°

	Figure Option View Download New Window
	图10 500 ℃ DT4C铁不同观测角度偏振度图像 (a): 5° ; (b): 25° ; (c): 55° Fig.10 Polarization images of 500 ℃ DT4C iron at different observation angles (a): 5° ; (b): 25° ; (c): 55°

	Figure Option View Download New Window
	图11 不同温度DT4C铁在5° 观测角度偏振度图像 (a): 300 ℃; (b): 400 ℃; (c): 500 ℃Fig.11 Polarization images of DT4C iron at different temperatures with 5° observation angle (a): 300 ℃; (b): 400 ℃; (c): 500 ℃

分别取300 ℃时粗糙度为0.61 μ m的铁以及0.65 μ m的钢进行加热。在收集到红外偏振图后, 对每种情况的线偏振度进行计算, 图12为样本铁, 钢在不同温度下的偏振度测量数据。

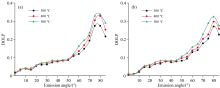	Figure Option View Download New Window
	图12 DT4C铁和45号钢在不同温度的DOLP测量结果 (a): DT4C铁; (b): 45号钢Fig.12 DOLP measurement results of DT4C iron and 45^# steel at different temperatures (a): DT4C iron; (b): 45^# steel

随着观测角度的增大, 金属表面的偏振度逐渐增大, 对比铁和45号钢的长波红外线偏振度值可知, 在相同温度下, 铁的长波红外线偏振度略高于45号钢。铁和45号钢在不同条件下的长波红外线偏振度峰值均保持在70° ~80° 范围内。对比同一金属不同温度的线偏振度变化曲线, 随着温度的增加, 金属的线偏振度略有提升, 在观测角度较小时, 各个温度的线偏振度未有明显的差别, 从50° 开始, 不同温度的线偏振度差异增大, 在峰值处, 这种差异更为明显, 图4仿真结果与图12实验结果的偏振度变化曲线都随着观测角度增大而增大, 但实验结果较仿真结果的数值偏大, 原因是实验时所采用的相机收集到的数据并不是单一谱段的数据, 而是长波范围内全谱段的数据积分之和, 仿真时仅仿真了单一谱段的偏振度数据, 因此实验结果比单一谱段红外偏振度仿真结果要高, 这与理论仿真结果相符。将温度范围扩展到150、 200以及250 ℃, 再次进行实验采集铁和45号钢材料的长波红外偏振度数据。

	Figure Option View Download New Window
	图13 DT4C铁和45号钢在不同温度的DOLP测量结果 (a): DT4C铁; (b): 45号钢Fig.13 DOLP measurement results of DT4C iron and 45^# steel at different temperatures (a): DT4C iron; (b): 45^# steel

在扩展多个温度后, 与图12所得的整体趋势结论相同, 随着温度的升高, 偏振度数据逐步增大, 在小角度处, 偏振度的变化并不明显, 随着观测角度的增加, 自50° 开始, 线偏振度差异越来越明显, 从峰值来看, 在低温处, 温度引起的偏振度差异并不明显, 温度越高, 其偏振度差异越明显。

4 结论

基于微面元理论的偏振BRDF模型推导得出红外辐射偏振传输Stokes表达式, 分析了其红外偏振特性与温度之间的关系; 基于理论推导趋势结果, 对不同温度的铁和45号钢进行了长波红外偏振探测实验。结果表明: 随着金属表面温度的升高, 金属目标的红外光谱积分偏振度也会有所增大, 同一温度下, 随着观测角度的增加, 金属表面的光谱的积分偏振度也在逐步增加, 峰值保持在70° ~80° 范围内。高温金属偏振特性对目标检测、红外辐射偏振对目标场景偏振特性、偏振成像系统性能预测、优化设计以及偏振图像处理研究等都有重要意义。

参考文献

文献列表

[1]	CAI Yi, HU Xu(蔡毅, 胡旭). Infrared and Laser Engineering(红外与激光工程), 2006, 35(6): 643. [本文引用:1]
[2]	Li Ning, Zhao Yongqiang, Pan Quan, et al. Optics Express, 2019, 27(2): 1376. [本文引用:1]
[3]	LI Jia-kun, JIN Wei-qi, WANG Xia, et al(李家琨, 金伟其, 王霞, 等). Infrared Technology(红外技术), 2014, 36(7): 513. [本文引用:1]
[4]	Zhang Lei, Guo Huijiao, Li Zhibo. Infrared Physics & Technology, 2019, 101: 127. [本文引用:1]
[5]	Sajid S, Hussain S, Sarwar A. Arabian Journal for Science and Engineering, 2019, 44(11): 9249. [本文引用:1]
[6]	ZHANG Ruo-lan, ZHANG Jin, LIN Yu, et al(张若岚, 张晋, 林宇, 等). Infrared Technology(红外技术), 2014, 36(2): 102. [本文引用:1]
[7]	ZHU Da-rong, YANG Shan-ji, WANG Fang-bin, et al(朱达荣, 杨善骥, 汪方斌, 等). Laser & Optoelectronics Progress(激光与光电子学进展), 2022, 59(4): 392. [本文引用:1]
[8]	WANG Jun, DING Na, LI Jian-jun, et al(王军, 丁娜, 李建军, 等). Journal of Applied Optics(应用光学), 2012, 33(3): 441. [本文引用:1]
[9]	E Yu-jia, WANG Tian-yu, GAO Ge, et al(鄂羽佳, 王天宇, 高鸽, 等). Advances in Mechanics(力学进展), 2018, 48: 201803. [本文引用:1]
[10]	WANG Zhen, HONG Jin, YE Song, et al(汪震, 洪津, 叶松, 等). Acta Photonica Sinica(光子学报), 2007, 36(8): 1500. [本文引用:1]
[11]	XU Wen-bin, CHEN Wei-li, LI Jun-wei(徐文斌, 陈伟力, 李军伟). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(1): 235. [本文引用:1]
[12]	XU Wen-bin, CHEN Wei-li, LI Jun-wei, et al(徐文斌, 陈伟力, 李军伟, 等). Infrared and Laser Engineering(红外与激光工程), 2017, 46(5): 94. [本文引用:1]
[13]	Jordan D L, Lewis G. Optics Letters, 1994, 19(10): 692. [本文引用:1]
[14]	Torrance K E, Sparrow E M. Journal of the Optical Society of America, 1967, 57(9): 1105. [本文引用:1]
[15]	Nicodemus F E, Richmond J C, Hsia J J, et al. Geometrical Considerations and Nomenclature for Reflectance. National Institute of Stand ards and Technology, Gaithersburg, MD, 1977. [本文引用:1]
[16]	WANG Jie-jun, WANG Peng, WANG Fang-yuan, et al(汪杰君, 王鹏, 王方原, 等). Acta Photonica Sinica(光子学报), 2019, 48(1): 73. [本文引用:1]
[17]	Hyde M W, Schmidt J D, Havrilla M J. Optics Express, 2009, 17(24): 22138. [本文引用:1]
[18]	YANG Yu-feng, WU Zhen-sen, CAO Yun-hua(杨玉峰, 吴振森, 曹运华). Acta Optica Sinica(光学学报), 2012, 32(2): 313. [本文引用:1]
[19]	ZHU Da-rong, FENG Kang-kang, WANG Fang-bin, et al(朱达荣, 冯康康, 汪方斌, 等). Laser & Optoelectronics Progress(激光与光电子学进展), 2020, 57(9): 210. [本文引用:1]
[20]	Bennett H E, Porteus J O. Journal of the Optical Society of America, 1961, 51(2): 123. [本文引用:1]
[21]	WANG Qi-chao, WANG Jia-chun, ZHAO Da-peng, et al(王启超, 汪家春, 赵大鹏, 等). Laser & Infrared(激光与红外), 2013, 43(11): 1260. [本文引用:1]

2006

0.0

... 0 引言近年来, 随着光电探测技术的不断进步, 红外成像技术作为一项重要的高新技术, 被广泛应用于军事^[1,2]、安防^[3]、医学检测^[4,5]、航空航天^[6]和目标探测^[7]等领域 ...

2019

0.0

2014

0.0

2019

0.0

2019

0.0

2014

0.0

2022

0.0

2012

0.0

... 红外偏振技术在反伪装识别方面已经开展了一些有价值的研究^[8] ...

2018

0.0

... 航天发动机、高速飞行器等人造物体通常温度可以达到几百摄氏度, 因此具有高温自辐射特性^[9] ...

2007

0.0

... 汪震等探讨了中温下铝面与钢制板材热红外偏振度与这些表面的粗糙度之间的关联, 得出的结论揭示了表面粗糙度降低会促使热红外偏振度提升的现象^[10] ...

2019

0.0

... 徐文斌等在较低温度下, 对两类伪装目标进行了高光谱偏振成像实验, 研究结果显示, 温度改变越大, 偏振特性提升量越大^[11] ...

2017

0.0

... 北京环境特性研究所实施了一系列高光谱偏振成像实验, 实验对象为在不同温度和不同观测角度下的涂漆和镀铝目标, 结果表明, 温度和观测角度对目标的偏振特性有较大影响, 目标表面的红外光谱偏振特性随辐射温度差值以及探测角度的差值增大而增大^[12] ...

1994

0.0

... m光谱处的不同粗糙度下铝板的红外偏振特性^[13] ...

1967

0.0

... 1 理论基础双向反射分布函数(bidirectional reflectance distribution function, BRDF)最早由Nicodemus在20世纪70年代定义^[14], 符号表示为f_BRDF ...

1977

0.0

... BRDF描述了物体表面在不同入射角下、任意观测角度的反射特性, 是用于表征物体表面光反射行为的一个函数^[15] ...

2019

0.0

... 在此, 微面元模型采用高斯分布来表述表面粗糙物体的微面元法线分布概率分布函数^[16] ...

2009

0.0

... Jones与Muller部分矩阵元之间的关系^[17]如式(8) ...

2012

0.0

... 表面反射系数随角度的变化可以被Minnaert模型很好的模拟出来, 故用该模型来表示漫反射部分的影响^[18] ...

2020

0.0

... C为范围为(-1, 0)的待定系数, Mjkd为漫反射的Muller矩阵元, 其中除 M00d=1, 其他元素均为0^[19] ...

1961

0.0

... 1961年, Bennett和Porteus假设表面高度服从高斯分布, 推导出了两者之间的关系^[20] ...

2013

0.0

... 由Stokes原理可知, 圆偏振分量通常较小, 可以忽略不计^[21], 得到 ...