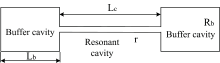
光声池结构参数有谐振腔半径r、 谐振腔长度L_c、 缓冲腔半径R_b、 缓冲腔长度L_b等, 如图1所示。 当缓冲腔长度等于谐振腔长度一半, 缓冲腔半径大于谐振腔半径3倍时, 缓冲腔对气体的缓冲效果最优^[16]。 因此, 设置缓冲腔长度等于谐振腔长度的一半(即L_b=0.5L_c), 缓冲腔半径等于谐振腔半径的3倍(即R_b=3r)。 在仿真过程中, 只有谐振腔半径和谐振腔长度两个变量。 在确定谐振腔半径和谐振腔长度尺寸后, 再确定缓冲腔半径具体参数, 进行光声池的有限元分析。 采用二维轴对称方式建立光声池仿真模型, 并对光声池模型做出适当优化处理, 忽略一些微小细节, 如位于缓冲腔上的进气孔腔、 出气孔腔、 微音器与谐振腔圆弧面之间的微小间隙、 缓冲腔与谐振腔之间由于密封O圈所致的微小间隙等。 形成简化后圆柱形光声池模型, 具体由一个谐振腔和两个对称的缓冲腔组成。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 圆柱形光声池Fig.1 Cylindrical photoacoustic cell

根据线性化声压波动方程, 参考文献资料^{[16, 17]}, 光声效应激发一阶纵向圆柱形共振腔, 基于光声效应, 相应的声压转化为光声信号的计算公式为

SPA=P0PmαabsCcell(1)

式(1)中, S_PA为光声系统响应值; P₀为激发光源在腔体内的功率; P_m为微音器的功率; α _abs为吸收系数; C_cell为一阶纵向简正模式的池常数, 其与光声池结构密切相关

Ccell=2(γ-1)LcQ100πVcω100(2)

式(2)中, γ 为等压和等容比热; L_c为谐振腔长度; Q₁₀₀为一阶纵向简正模式的品质因数; V_c为光声腔体积; ω ₁₀₀为一阶纵向简正模式的声共振频率, 等于 v2Leff, v为声速。

根据对谐振腔几何参数的分析, 选定谐振腔半径范围在4~10 mm, 长度范围在70~160 mm, 运用参数化扫描功能对谐振腔半径和长度进行同步仿真分析。 由图2可知, 光声池声压与谐振腔半径成反比, 与谐振腔长度成正比, 谐振腔半径相比于谐振腔长度对声压的影响更为剧烈。 光声池的设计目标即为获得较大的声压。 因此, 谐振腔应选择较小的半径参数。 从图2可以看出, 在相同的谐振腔长度参数下, 半径为4 mm的光声池声压要明显大于其他半径参数下的声压值。 结合前述分析知, 谐振腔半径应至少大于等于4 mm, 故谐振腔半径选为4 mm。

图2

Fig.2

	Figure Option ViewDownloadNew Window
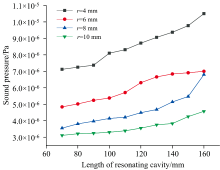	图2 声压与光声池几何参数的关系Fig.2 Relationship between sound pressure and geometrical parameters of photoacoustic cell

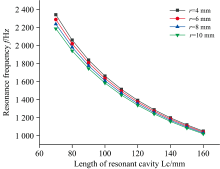
谐振腔长度的选择不能单一的追求声压值最大化, 应从以下几点来综合考虑, 如图3所示。 首先, 光声池共振频率与谐振腔半径和长度成反比, 且共振频率对谐振腔长度较为敏感。 在谐振腔半径确定的情况下, 光声池的共振频率主要受谐振腔长度影响, 故谐振腔长度的选择应着重考虑对共振频率的影响。 为了减少环境低频噪声对系统信噪比的影响, 共振频率不能过低。 但过大的共振频率会使光热声转换效率降低, 故通常要求共振频率在1~2 kHz。 其次, 从提高声压值角度谐振腔长度不宜过小, 且长度160 mm效果更好。 但是在腔体加工过程中, 要保证8 mm孔径的一次性钻孔成型、 精准度、 粗糙度和后期抛光处理等加工质量, 难度较大。 综上所述, 谐振腔长度的选择受多种因素制约。 本文在兼顾声压、 共振频率及加工因素的影响下, 确定谐振腔长度为120 mm。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 共振频率与谐振腔长度的关系Fig.3 Relationship between resonant frequency and resonant cavity length

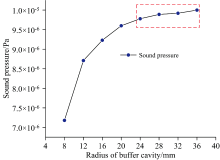
确定谐振腔半径为4 mm, 长度为120 mm后, 根据文献的理论所述, 缓冲腔长度即为60 mm^[17]。 设置缓冲腔半径分别为谐振腔半径的2~9倍, 仿真分析缓冲腔半径对光声池声压的影响规律, 仿真结果如图4所示。 由图可知, 光声池声压随缓冲腔半径的增大而增大, 且增大趋势逐渐较小。 仿真结果较好地验证了文献的理论。 当缓冲腔半径大于24 mm时, 声压增大的幅度已很小。 考虑到光声池的小型化, 确定缓冲腔半径为24 mm。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 声压与缓冲腔半径的关系Fig.4 Relationship between sound pressure and buffer cavity radius

光声池结构与尺寸是影响光声信号的关键因素, 合理的腔体形状可以一定程度上增强光声信号。 H型圆柱形光声池缓冲腔和谐振腔之间为直角连接, 腔体结构上存在尺寸的突变, 不利于待测样气进入谐振腔发生光声效应。 为解决这一问题, 提出一种圆柱圆台复合缓冲式光声池, 如图5所示。 具体优化思路: 以仿真所得光声池结构尺寸为基础, 保持谐振腔几何形状和尺寸不变、 缓冲腔长度和半径尺寸不变, 仅对缓冲腔形状进行优化, 将原圆柱形缓冲腔优化为圆柱与圆台相结合的缓冲腔。 圆柱圆台复合缓冲式光声池的设计参数有: 圆台底圆半径R和圆台高度H。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 圆柱圆台复合光声池腔体结构Fig.5 Composite photoacoustic cell structure with cylindrical circular platform

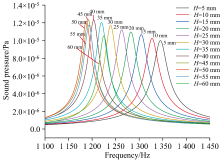
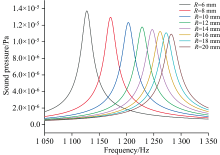
在有限元仿真软件中, 按照圆台底圆半径为10 mm建立光声池模型。 保持其他参数不变, 对圆台高度设置参数化扫描, 扫描范围为5~60 mm, 步长为5 mm。 仿真分析得到圆台高度对光声信号声压的影响, 如图6所示。 可知, 当其他参数不变时, 光声信号声压值随圆台高度的增加呈现先增大后减小的趋势。 当圆台高度大于45 mm时, 光声信号声压值小幅降低。 这说明圆台高度并非越大越好, 且圆台高度的选择必须合理, 否则不利于光声信号的提升。 可以看出, 相比于原所设计的圆柱形光声池9.78× 10^-6 Pa的声压值, 圆柱圆台复合缓冲式光声池的声压值提升了一个数量级。 与此同时, 改变圆台高度使光声池腔体共振频率发生明显变化, 共振频率随圆台高度的增加表现为先减小后增大的趋势。 从图中可以看出, 圆台高度最优范围在40~50 mm。 同理, 设置圆台高度为40 mm, 保持其他参数不变, 对圆台底圆半径设置适应实际尺寸和切实改进需求的参数化扫描, 扫描范围为6~20 mm, 步长为2 mm。 半径扫描范围不低于6 mm, 一是因为过小的半径虽然可以增加绝对声压值, 但是谐振腔的共振频率随着半径的减少而减小, 而过低的共振频率不利于激光的调制, 易造成低频噪声影响系统的信噪比。 二是因为谐振腔为了匹配二极管激光器(DL-405, 光束发散角< 1 mrad, 准直光斑~10 mm, 准直发散角< 8 mrad)的需要, 其半径设计为4 mm, 相应的圆台底圆半径不能小于它。 综上, 设置扫描范围为6~20 mm。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 圆台高度对光声信号声压的影响Fig.6 Effect of circular table height on sound pressure of photoacoustic signal

仿真分析得到圆台底圆半径对光声信号声压值的影响, 如图7所示。 可见, 当其他参数不变时, 光声信号声压值随圆台底圆半径的增加而减小。 同时, 改变圆台底圆半径也使光声池腔体共振频率发生明显变化, 共振频率随圆台底圆半径的增加而增大。 造成以上结果的原因在于, 圆台底圆半径的改变相当于一定程度上改变了谐振腔的长度, 使光声池池常数增加, 池常数与光声信号成正比。 而光声池共振频率与谐振腔长度成反比。 进而可以推断, 当圆台底圆半径越小, 圆台高度越大, 光声池声压值则越大, 光声池共振频率则越小。 在此, 从光声信号声压值角度来看, 圆台底圆半径最优解为6 mm。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 圆台底圆半径对光声信号声压的影响Fig.7 Influence of the radius at the bottom of a circular table on the sound pressure

本文以光声信号声压值作为评价指标, 每个因素选取3个水平, 各因素水平之间相互独立, 互不影响。 设计两因素三水平正交试验, 选用L₉(3²)型正交试验表。 其中, 圆台高度和圆台底圆半径分别对应因素A和因素B, 且分别对不同圆台参数组合进行有限元仿真分析, 因素水平表和正交试验方案及仿真结果如表1所示。

表1

Table 1

表1(Table 1)

表1 因素水平表和正交试验方案及仿真结果分析 Table 1 Orthogonal test scheme and result analysis 试验号 圆台高度 A/mm 圆台底圆 半径B/mm 试验 方案 光声信号 声压值/Pa 1 40 6 A1B1 1.373× 10-5 2 40 8 A1B2 1.296× 10-5 3 40 10 A1B3 1.233× 10-5 4 45 6 A2B1 1.399× 10-5 5 45 8 A2B2 1.303× 10-5 6 45 10 A2B3 1.236× 10-5 7 50 6 A3B1 1.379× 10-5 8 50 8 A3B2 1.299× 10-5 9 50 10 A3B3 1.219× 10-5

表1 因素水平表和正交试验方案及仿真结果分析 Table 1 Orthogonal test scheme and result analysis

显然光声信号声压值越大, 则表示此参数组合下的光声池性能越好。 为了得到圆台的最佳参数组合, 对正交试验结果进行极差分析, 如表2所示。 K(1~3)反映的是对应因素下具体水平时的试验数据和, k(1~3)反映的是对应K值的平均值, 每列的极差R反映的是该因素对圆台正交试验结果的影响程度, 极差越大说明该因素对试验评价指标的影响就越大。 由表2可知, R_B> R_A, 故圆台底圆半径对试验结果的影响较大, 圆台高度的影响较小。 由表1可知: 试验号4的光声信号声压值最大, 表明此参数组合下的光声池性能最优。 因此, 得圆台最优参数组合为: 圆台底圆半径为6 mm, 圆台高度为45 mm。

表2

Table 2

表2(Table 2)

表2 试验结果极差分析 Table 2 Range analysis of test results 因素 圆台高度A 圆台底圆半径B K1 3.902× 10-5 4.151× 10-5 K2 3.938× 10-5 3.898× 10-5 K3 3.897× 10-5 3.688× 10-5 k1 1.301× 10-5 1.384× 10-5 k2 1.313× 10-5 1.299× 10-5 k3 1.299× 10-5 1.229× 10-5 极差R 1.40× 10-7 41.55× 10-6 因素主次 BA 最优方案 A2 B1

表2 试验结果极差分析 Table 2 Range analysis of test results

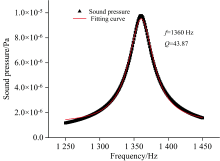
对优化前的光声池尺寸参数进行建模仿真分析, 设置频率扫描范围为1 250~1 450 Hz, 步长为1 Hz。 如图8所示, 对声压数据点进行Lorentz曲线拟合得声压峰值对应的频率为1 360 Hz, 即光声池的共振频率为1 360 Hz, 可求得品质因数为43.87。 可见, 在1 360 Hz下光声池内最大声压值为9.78× 10^-6 Pa, 声压表现为谐振腔中高, 两侧缓冲腔中低。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 光声池频率响应曲线Fig.8 Frequency response curve of photoacoustic cell

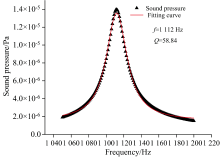
以正交试验所得最优方案参数, 对优化后的光声池进行建模仿真分析, 如图9所示, 对声压数据点进行Lorentz曲线拟合得声压峰值对应的频率为1 112 Hz, 可求得品质因数为58.84。 优化后的光声信号声压值为1.40× 10^-5 Pa, 优化后相比于优化前光声信号声压值提升43.15%, 且优化后的光声池声场分布未发生变化; 由理论分析知, 共振频率越小光声信号幅值越大, 而优化后的光声池共振频率在取值范围内进一步降低, 有利于光声信号幅值的提升; 优化后和优化前的光声池品质因数分别为58.84、 43.87, 优化后的光声池品质因数相比于优化前提升34.12%。 综上所述, 将单一的圆柱形缓冲腔优化为圆柱与圆台相结合的复合式缓冲腔可有效地提高光声信号声压值与品质因数。 同时, 优化后的光声池体积进一步减小, 有助于光声池的小型化。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 优化后光声池频率响应曲线Fig.9 Frequency response curve of optimized photoacoustic cell

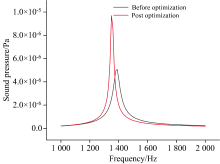
为了验证圆柱圆台复合缓冲式的H型共振光声池的优化效果, 对其进行有限元仿真模拟分析, 模拟分别通入不同气体并计算分析其影响特性。 这里使用二氧化碳、 氮气和甲烷为研究对象。 在COMSOL软件中, 选取热粘性声学模块, 对光声池进行二维轴对称建模。 在光声池的中心轴线上, 放置一线热源, 来模拟激光对气体分子进行激发。 光声池腔内压强稳定在1 atm, 温度设置为293 K。 由图10、 图11、 图12可知: 在通入不同气体后, 各气体的光声信号分别为2.18× 10^-5、 1.12× 10^-5和9.70× 10^-6 Pa, 相比于优化前, 优化后的光声池光声信号声压值均有不同程度的提升, 光声池共振频率在取值范围内进一步降低, 且在一阶共振频率下有更好的响应特性。

图10

Fig.10

	Figure Option ViewDownloadNew Window
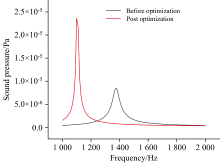	图10 优化前后光声池内CO2气体频率响应曲线Fig.10 The frequency response curves of CO2 gas in the photoacoustic cell were optimized

图11

Fig.11

	Figure Option ViewDownloadNew Window
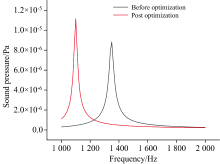	图11 优化前后光声池内N2气体频率响应曲线Fig.11 The frequency response curves of N2 gas in the photoacoustic cell were optimized

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 优化前后光声池内CH4气体频率响应曲线Fig.12 The frequency response curves of CH4 gas in the photoacoustic cell were optimized