TDLAS波长调制技术通过对激光器注入电流进行激光波长扫描和波长调制, 即在激光器两端注入三角波电流, 且同时在此基础上增加一个幅值较小的高频正弦变化, 此时, 激光器输出光强和输出波长可表示为

I-0(t)=I01u(t)+ηsin(ωt+φ)](1)

λ(t)=λ0+λmsin(ωt)(2)

式中, u(t)为锯齿波信号, η 为光强的调制幅度, φ 为光强与波长调制的相位差, λ ₀为光源的中心波长, λ _m为波长的调制幅度, 根据朗伯-比尔定律

I(t)=I-0(t)e-α(λ)Lc(3)

式(3)中, I-0(t)为入射光强, α (λ )为气体分子的吸收系数, L为气体吸收光程, c为气体的浓度, I(t)为出射光强。 当光源中心波长与气体吸收谱线中心波长相等时, 激光出射光强为

I(t)=I01ηsin(ωt)]-I0α0Lc1+λmsin(ωt)Δλ2(4)

气体吸收系数可以用Lorentz线型函数表示。 对式(4)进行傅里叶级数展开, 得到二次谐波信号的幅值

I2f=-kλ0α0Lc(5)

式(5)中, k为λ _m和Δ λ 的函数。 由此可知, 二次谐波信号幅值与气体浓度有关, 解调出二次谐波便可计算出气体浓度。

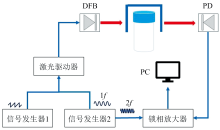
基于TDLAS技术的CO₂浓度检测实验装置如图1所示。 使用中心波长为4 989.87 cm^-1可调谐分布反馈式(DFB)二极管激光器(nanoplus DFB Laser 2 004 nm)作为激光光源。 通过信号发生器1产生10HZ低频三角波信号叠加信号发生器2产生16 kHZ高频正弦波信号控制激光驱动器(standford research systems LDC501)使得激光器输出激光波长可调。 出射激光经过激光准直器准直后穿过配备气瓶, 吸收光路长度为3 cm。 激光经过光谱吸收后, 由InGaAs光电检测器(PD)接收将光信号转换成电压信号, 并交由锁相放大器将二次谐波信号解调出来。 最后, 对收集到的谐波信号传入PC端进行滤波处理并根据式(5)计算样品气体的瞬时浓度值, 从而实现气体浓度的全自动检测。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 TDLAS气体检测装置示意图Fig.1 Schematic diagram of TDLAS gas detection device

实验选取的CO₂的吸收谱线为4 989.97 cm^-1, 其中心波长为2 004 nm, 在此波长区域有很强的吸收, 且无其他气体干扰。 在大气压强为1 atm、 温度为298 K条件下, 通过调谐电流控制激光器波长扫描二氧化碳分子吸收峰。

神经网络模型预测的质量往往取决于实验数据集的数量, 但是通过实验获得大量数据集是非常困难的, 同时, 在实验中无法获得完美的谐波信号, 无法满足神经网络训练要求。 因此, 为了解决实验数据稀缺和理想二次谐波信号无法获取的问题, 利用HITRAN应用程序, 在实验条件下, 模拟与真实实验信号分布相同的2 500条不同浓度的CO₂吸收光谱, 用于训练、 评估和测试本文提出的去噪网络模型, 以提高模型的泛化能力。 具体来说, 模拟CO₂浓度范围为0~25%(步长为0.01%), 谱线强度设置为0.031 9, 选择Lorentz线型以拟合吸收线。

在TDLAS真实测量系统中, 谐波信号中的噪声形式主要包括高斯白噪声和干涉噪声。 其中高斯白噪声主要是由电子器件产生的散粒噪声和热噪声, 散粒噪声和热噪声具有白噪声的频谱特性, 服从高斯分布, 是一种随机信号; 干涉噪声主要是由实验系统中激光反射和散射引起的光学条纹的干扰。 干涉噪声等效于在谐波信号上增加了一个缓慢变化的干扰信号, 引起谐波吸收信号基线漂移。 两种噪声干扰叠加从而影响气体检测精度和稳定性。 根据上述噪声分析理论和真实谐波信号大小进行噪声模拟, 首先, 通过高斯白噪声(均值为0, 方差为7.6× 10^-5)和干涉噪声(Airy函数)模拟系统的白噪声及光学条纹干扰, 然后叠加在模拟的纯净二次谐波信号上, 最后得到一个带有噪声的二次谐波信号仿真数据集。

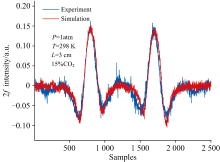
此外, 通过实验收集了浓度为0%, 5%, 10%, 15%, 20%五组CO₂透射谐波光谱(将空气中二氧化碳含量近似认为0%), 每组浓度测量1 000次, 形成了一个实验数据集, 以评估通过在仿真数据集上训练的TGDF算法在实际应用中的滤波性能。 在实验数据集中选择一组浓度的谐波信号与仿真信号进行比较, 如图2所示。 通过计算两个信号之间的皮尔逊相关系数来评估它们之间的相似度, 相关系数(R)=0.98, 可以说明仿真数据可以很好地拟合实验结果, 但是在图2中, 仍可以看到理论波形和实际波形之间存在一定误差, 产生这种误差的原因有两个: (1) 由于在测量过程中, 实际的压强、 温度以及气体浓度分量与理论模拟的数值存在一定程度上差异, 进而影响吸收线型的半高全宽, 导致实际测量和理论模拟的二次谐波线形存在轻微偏差。 (2) 二次谐波信号在非中心吸收位置的线形会受剩余幅度调制中的相位差影响, 由于本工作不考虑相位差因素, 因此二次谐波在非中心吸收位置的理论线型与实际线形会存在较小的差异。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 仿真模拟的光谱信号与真实实验信号对比Fig.2 Comparison of the simulated spectral signals with the experimental signals

TGDF模型架构如图3(a)所示, 由神经网络谐波信号去噪模块(HSD)和奇异值分解(SVD)降维重建两部分组成, 如图3(b)所示。 神经网络去噪模块由5个全连接层、 2个激活函数和2个采样块构成, 首先通过一个全连接层, 后接一个Relu激活函数以提高非线性表达能力, 再接一个全连接层, 将二氧化碳气体透射光强二次谐波信号投射到一个新的特征域, 得到相应的特征图。 然后将特征图传入采样块操作, 在特征域上进行去噪处理。 采样块操作包括2倍上采样以增加模型对光谱细节的捕捉能力, 然后进行平均池化操作。 平均池化去噪平滑度高, 尤其适用于高频振动信号的平滑处理, 它可以把特征图维度还原回来, 同时减少模型参数和计算量。 将窗口大小设为8, 步长设为2, 得到初步的去噪光谱特征图。 再次重复上述操作, 最后, 连接一层全连接层将特征域信号尺度还原回来, 得到第一阶段的去噪光谱。

图3

Fig.3

	Figure Option ViewDownloadNew Window
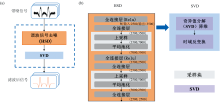	图3 (a) TGDF滤波器的数据处理流程图; (b)TGDF 网络结构Fig.3 (a) Data processing flowchart of TGDF filter; (b) TGDF network structure

之后, 引入奇异值分解进行降维去噪处理, 在进一步调整谐波信号的同时最大限度地保留原始信息, 将第一阶段去噪后一维光谱信号连续截断使其转变为二维矩阵, 矩阵大小为(m, n), 具体计算过程如式(6)所示

Xm×n=Um×nΣm×nVTn×n(6)

式(6)中, Σ _{m× n}为实对角矩阵, Σ _{m× n}=diag(λ ₁, λ ₂, …, λ _q), q=min(m, n), λ _q为矩阵Σ _{m× n}的非零奇异值。 在奇异值分解中矩阵Σ _{m× n}对角线上的前k个奇异值表征X_{m× n}矩阵中信号子空间的分量, k称为对信号重构的有效阶次, 保留k阶降维后数据可表示为

X'm×k=Xm×nVTk×n(7)

最后, 将降维后信号利用式(7)将压缩后数据反变换为时域信号, 得到最终的滤波信号。

对仿真数据集使用五折交叉验证来进行超参数选择和模型验证, 均方误差(MSE)作为损失函数, 表达公式为

MSE=1n∑i=1m(yi-y^i)2(8)

式(8)中, i表示对应于整个光谱数据点的索引, y^i是神经分离器在位置处的预测传输值, y_i是在位置的实际传输值, 并且m是预测输出的数据点的数量(m=2 500)。 利用梯度下降法来优化损失函数并得到模型的最佳参数, Adam算法作为模型优化函数。 在训练过程中当batch为40时模型有最优的滤波性能, 并且模型在1 000个epochs内收敛。

在仿真测试数据集上, 随机选择一组CO₂气体波长调制光谱作为代表样本, 以直观地比较TGDF与EMD、 SG和小波变换等传统时-频域滤波算法及MLP全连接神经网络算法的滤波效果, 如图4所示。 EMD将含噪数据分解为一系列固有模态函数(IMFs), 并对每个IMFs进行特征识别, 对识别为噪声的IMFs进行去噪处理。 将有噪声的二次谐波信号分解为七个IMF, 保留最后四个IMF的总和进行去噪时结果最好, 信噪比为10.77 dB。 SG滤波算法滤波效果受窗口长度和拟合阶数选择的限制。 当滤波窗口点数设为151, 拟合阶数为2时, 滤波效果最好, 信噪比为11.43 dB。 小波变换通过选择合适的小波基函数、 分解层数和阈值能很好地表达出序列中的突变和非平稳部分。 选择“ db18” 作为小波基函数, 并通过软阈值进行去噪, 最终得到的信噪比为12.62 dB。 MLP滤波算法由三层全连接层和2个Relu激活函数组成(batch=32, lr=1× 10^-5), 最终信噪比为20.42 dB, 与原始信号相比增加13.5 dB。 与上述滤波算法相比, TGDF去噪方法获得的二次谐波曲线信噪比最高, 与原始信号相比增加了15.07 dB(从7.34 dB增加到22.41 dB, 其中不引入奇异值分解滤波, 可以将信噪比增加到21.95 dB)。 结果表明, TGDF具有最优的滤波性能, 可以很好地消除噪声干扰, 并能保持信号的真实性。

图4

Fig.4

	Figure Option ViewDownloadNew Window
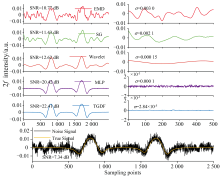	图4 几种滤波算法对模拟噪声二次谐波信号的滤波效果比较Fig.4 Comparison of filtering effects among several filtering algorithms for simulated noisy second harmonic signal

计算谐波信号的非吸收区域(前500个数据点)波动的标准差评估各滤波算法去噪后的波动幅度, 如图4所示。 EMD、 SG和小波变换滤波算法在非吸收区域波动幅度较大, 虽然能够很好地消除突变干扰, 但对调制引入的与吸收信号同频同相的低频干扰无能为力。 相比之下, MLP神经网络算法摆脱了时域和频域的限制, 能够很好地去除低频噪声, 但仍保留一定的波动幅度和突变信号。 TGDF 算法滤波后信号比MLP神经网络算法更加平滑, 且波动幅值仅为MLP滤波算法的28%, 能够更好地去除谐波信号中的低频噪声, 使输出信号更接近理论信号。

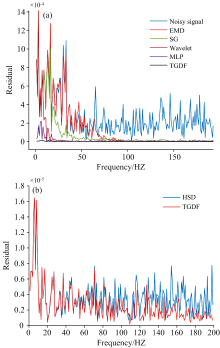
此外, 从频域的角度对TGDF滤波性能进行了表征, 通过快速傅里叶变换获得各种滤波算法处理后光谱信号的频率残差分布。 如图5(a)所示。 EMD、 VMD和小波变换滤波更专注于滤波高频分量, 无法很好地滤除掉低频分量, 这与图4中非吸收区的平滑效果一致。 MLP滤波算法虽然能够滤除低频分量但在低频区域还具有较大的残差。 TGDF滤波算法几乎完美的滤除高频噪声分量, 即使在低频区域也能保持最低的残差, 这是滤除噪声和保留吸收信息的关键。 图5(b)表明, HSD是TGDF滤波算法降低低频噪声的主要贡献者, 能够几乎全部消除整个频率域中的噪声。 其中, 采样块结构是降低低频噪声的关键, 采样块结构在特征域上直接滤除掉噪声分量, 与直接学习纯净噪声相比更能精准捕捉并滤除低频分量, 从而使得在低频区域HSD比MLP有更低的噪声残差。 奇异值分解仅能够滤除残余的高频噪声分量, 进一步平滑信号和提高信噪比。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 原始及滤波后光谱信号的频率残差分布Fig.5 The frequency residual distribution of the original and filtered spectral signals

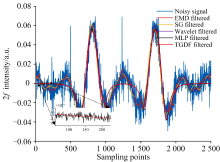
为了验证TGDF滤波算法在实际应用中的可靠性, 将TDLAS气体检测装置获得的五组CO₂谐波信号经过TGDF算法滤波处理, 并以5%CO₂浓度实验测量的二次谐波信号作为代表样本, 直观地比较了几种算法的噪声抑制效果, 如图6所示。 蓝色线表示未经任何滤波算法处理的二次谐波信号, 由于残余幅度调制和光强调制的影响, 导致实验数据的二次谐波信号不对称, 且携带大量噪声信号。 从图中可以看到, EMD、 SG和小波变换滤波算法能够很好地抑制谐波信号吸收区域和非吸收区域中的高频噪声, 使其输出光滑, 但在非吸收区域还是有较大的幅值波动, 影响其测量浓度结果的准确性和稳定性。 MLP和TGDF滤波算法能够很好地去除全频段噪声, 但在非吸收区域TGDF滤波后信号比MLP滤波更加平滑, 更接近真实信号, 与模拟数据集的评估结果一致, 证明了TGDF滤波算法在真实实验数据集上具有良好的泛化性能。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各种滤波算法的去噪效果Fig.6 Denoising effect of various filtering algorithms

3.2.1 检测精度评估

将收集到的五组实验谐波信号经TGDF滤波后对二次谐波信号最大值[max(2f)]与气体浓度进行线性拟合, 拟合结果如图7所示。 线性关系拟合为y=0.743 8x+0.081 4, 线性相关性系数R²=0.998, 二次谐波幅值与CO₂气体浓度之间存在良好的线性关系, 通过拟合公式可以实现CO₂气体浓度的精确反演。 根据拟合公式对五组CO₂二次谐波信号进行气体浓度反演, 并于其他算法的测量结果进行比较, 测量平均绝对误差如表1 所示。 TGDF滤波算法处理后测量绝对误差在各气体浓度之间均低于其他滤波算法。 由此可见, 在实际应用中, 经TGDF滤波算法处理后的CO₂气体检测精度优于其他算法。

图7

Fig.7

	Figure Option ViewDownloadNew Window
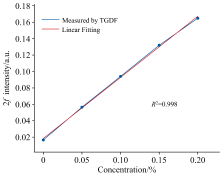	图7 二次谐波振幅(max)与CO2浓度之间的线性关系Fig.7 Linear relationship between second harmonic amplitude (max) and CO2 concentration

表1

Table 1

表1(Table 1)

表1 各种滤波算法的平均绝对误差 Table 1 Average absolute error of each filtering algorithm 方法 各浓度测量的平均绝对误差/% 0% 5% 10% 15% 20% 原始数据 2.30 1.10 0.93 1.10 1.40 EMD 0.42 0.37 0.39 0.30 0.46 SG 0.40 0.40 0.47 0.35 0.38 Wavelet 0.47 0.39 0.43 0.29 0.36 MLP 0.30 0.28 0.25 0.30 0.32 TGDF 0.27 0.20 0.23 0.28 0.32

表1 各种滤波算法的平均绝对误差 Table 1 Average absolute error of each filtering algorithm

3.2.2 检测稳定性评估

为了衡量和评价经TGDF算法滤波后TDLAS气体检测系统的稳定性。 比较连续测量的TGDF降噪前后五组CO₂浓度结果, 如图8所示。 原始测量数据受到激光功率振动、 光学器件噪声、 后续电路噪声的影响, 导致浓度测量有明显波动, 该波动在用TGDF算法处理后明显减小。 表2为二次谐波实验信号数据和各滤波算法处理后的二次谐波数据浓度反演的标准差, 从表中可以看出, 20%CO₂测量稳定性较差, 可能是在测量过程中受激光器功率震动的影响最大, 导致测量浓度基线明显漂移。 EMD滤波算法在0%CO₂测量稳定性最差, 这是由于EMD在分解时难以准确提取出弱信号成分, 导致无法有效去除在低浓度时的信号噪声。 此外, 在测量其他浓度时, SG滤波算法的检测标准差最高, 稳定性最差, 这是因为SG滤波是基于局部多项式拟合, 在测量的谐波信号中存在大量的突然变化和尖峰, SG滤波算法可能会错误地平滑这些区域, 导致测量结果不稳定。 然而, 经TGDF算法优化后的五组气体检测标准差均低于其他算法, 能够很好地识别吸收信号并将噪声干扰滤除, 从而检测稳定性得到了显著提升。

图8

Fig.8

	Figure Option ViewDownloadNew Window
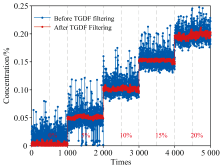	图8 TGDF降噪前后连续测量结果Fig.8 The continuous concentration test results before and after TGDF noise reduction

表2

Table 2

表2(Table 2)

表2 降噪前后测量的标准差 Table 2 Standard deviation of measurements before and after noise reduction 方法 各浓度测量的标准差/% 0% 5% 10% 15% 20% 原始数据 1.60 1.07 0.78 0.77 0.64 EMD 0.44 0.26 0.27 0.23 0.32 SG 0.29 0.40 0.38 0.30 0.47 Wavelet 0.23 0.19 0.22 0.20 0.28 MLP 0.20 0.19 0.21 0.15 0.30 TGDF 0.19 0.14 0.15 0.13 0.25

表2 降噪前后测量的标准差 Table 2 Standard deviation of measurements before and after noise reduction