作者简介: 姜志全, 1975年生,中国科学技术大学理化科学实验中心高级工程师 e-mail: jzhiquan@ustc.edu.cn
X射线光电子能谱(XPS)技术广泛应用于科学研究和工程技术领域。 测试数据通常需要进行谱峰拟合处理, 才能得到准确的谱峰结合能位置和表面物种的相对含量信息。 但XPS谱峰拟合过程存在着严重的人为因素, 使得拟合结果存在着比较明显的错误。 造成拟合错误的原因主要就是对谱峰信号的拟合参数没有做任何限定, 或者做出了错误的限定。 光电子信号有4个基本要素, 即自旋轨道分裂间距、 分裂谱峰强度、 谱峰的形状和对称性、 谱峰的半高峰宽。 文章阐述了这4个基本要素的物理本质, 并且给出了拟合参数设置的合理建议。 XPS谱峰拟合并不是简单地做数值运算, 而是需要对光电子信号的上述4个基本要素做合理的关联与约束, 使得拟合后的总包络线与原始谱线尽量吻合, 并且各分谱都具有明确的物理化学意义。
X-ray photoelectron spectroscopy (XPS) has been widely employed in scientific research and engineering technology. The test data typically require handling for peak fitting; consequently, an accurate peak position in binding energy and the relative contents of the surface species are required. However, a serious human factor emerges during the process of XPS peak fitting, leading to distinct mistakes in the fitting results. The reason for the fitting errors is primarily that no constraints or incorrect constraints were applied to the fitting parameters of the XPS signals. There are four essential elements in XPS photoelectron signals: the separation distance and intensity ratio of spin-orbit splitting, the shape and symmetry of XPS signals, and the full width at half-maximum (FWHM) of XPS signals. In this text, the physical natures of these four essential elements are elucidated, and a reasonable suggestion is proposed for the setting of parameters in XPS peak fitting. In the process of XPS peak fitting, it is not simply a matter of mathematical calculation. However, association and constraintmust be considered in the above four essential elements of XPS photoelectron signals, resulting in a large extent of coincidence between the fitting envelope and the original curve. Furthermore, the components after peak fitting all possess explicit physical and chemical meanings.
在现代科研领域中, 通常需要各种分析测试技术对样品进行表征, 得到样品的物理化学性质, 并与其性能和应用关联起来, 建立相应的构效关系, 从而能够对进一步的科学研究和生产制备提供理论指导。 X射线光电子能谱(XPS)技术是一种无损分析检测手段, 对于大多数固体样品, 常规XPS的检测深度约为1~10 nm。 通过XPS检测分析, 不仅可以得到样品表面的元素组成及其相对含量, 更重要的是, 可以得到表面元素的化学态和样品的电子结构信息[1]。 近年来, 随着太阳能电池和离子电池等新能源技术的蓬勃发展, XPS技术对于这些新能源材料的表面/界面的化学性质表征具有独特的优越性, 因而得到越来越广泛的应用。
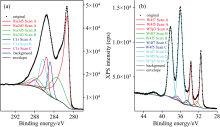
在进行XPS数据处理和分析的过程中, 经常会需要进行谱峰拟合[2, 3]。 谱峰拟合可以使彼此靠近重叠的信号得以分离, 从而分别精确测定各自的结合能数值及其相对含量。 首先, 不同元素的不同轨道电子的光电发射信号可能会产生交叠, 此时就需要进行谱峰拟合, 从而对表面物种进行准确的定性定量分析。 例如在测试某含Ru的样品体系时, 如图1(a)所示, C(1s)光电子信号和Ru(3d)光电子信号交织在一起, 采用谱峰拟合技术对测试数据进行分解, 一方面是将Ru(3d)光电子信号分离出来, 以便于开展精确的定性定量分析工作, 另一方面是可以得到准确的外来污染碳物种的C(1s)谱峰结合能数值, 利用这个结合能数值来进行XPS数据的荷电校正处理。
如果同一元素在样品表面上有多种不同化学状态的物种同时存在, 同样需要进行谱峰拟合, 从而得到这些物种的精确结合能数值及其相对含量, 能够更好地对XPS光电子信号进行归属。 如图1(b)所示, 长期放置于空气中的钨金属片上存在着一层天然氧化物层, 通过对W(4f)谱峰拟合后, 可以明确地分辨出4种不同化学状态的光电子信号, 分别对应着金属态和不同氧化程度的钨物种, 表面钨物种的具体结合能数值及其相对比例也一并获得。 通过XPS谱峰拟合, 孙柏玲等[4]研究发现, 随着热处理温度的升高, 落叶松木材纤维素中木质素-碳水化合物含量增加, 使得仅与C或H原子键合的C原子的比例提高, 而热处理木材分离提取的纤维素碳链缩短, 使得样品中C— O和C=O/O—C—O键合的C原子的比例降低。
但是, 谱峰拟合受到多种因素的影响。 在拟合过程中, 需要对拟合参数做一定的设置和约束, 并且这些拟合参数并不是固定不变的, 没有一套万能参数可以适用于所有样品的XPS谱峰拟合。 这些拟合参数随着测试仪器、 实验条件和样品自身化学状态的不同而需要进行调整, 这样拟合得到的结果才能更加真实地反映样品自身的化学状态。 不同的拟合参数会导致不同的谱峰拟合结果。 如果拟合参数设置不合理, 会得到错误的拟合结果, 从而对XPS测试结果做出错误的谱峰归属和数据解析。 就XPS谱峰拟合中的参数设置, 本文给出一个详细的阐述, 并结合一个具体的样品案例展示了XPS谱峰拟合过程。
文中的所有数据均是在热电公司ESCALAB 250Xi型电子能谱仪上获得。 能谱仪系统的分析室基压为2.0× 10-10 mbar。 以单色化Al Kα 辐射线(hν =1 486.6 eV)为激发源, 由半球能量分析器收集光电子信号, XPS全谱扫描的通过能设为100 eV, 精细谱扫描的通过能设为30 eV。 以外来污染碳物种的C(1s)光电子信号结合能284.80 eV为参考, 所有的实验数据已做荷电校正处理。
在光电离过程中, 电离后产生的光电子如果能量无损地从样品中逸出而被检测到, 就构成XPS测试谱图中的谱峰信号。 另外, 还有部分电子在此过程中发生了能量损失, 由于失去能量特征而构成XPS测试谱图中的本底信号。 所以, 在进行XPS定量计算和谱峰拟合时, 首先要扣除掉本底信号。 在XPS数据分析中, 常用的本底扣除算法有线性本底、 Shirley本底和Tougaard本底等。
最简单的本底扣除方法是在感兴趣的谱峰两端指定点之间作直线, 也就是线性本底。 其计算公式如式(1)所示, 其中a为直线的斜率, b为直线在强度轴上的截距。
但这种方法通常误差较大, 并没有物理意义。 XPS中大多数谱峰有严重的非弹性散射光电子, 谱图上表现为谱峰两端的本底明显不同, 高结合能端的本底通常高于低结合能端的本底, 此时采用线性本底方法就存在着谱峰两端取点位置的选择问题, 取点的位置不同, 对定量计算和谱峰拟合的结果有较大的影响。
目前最常用的本底扣除方法是由Shirley提出的。 Shirley方法是一种非线性本底扣除方法, 具有明确的物理意义。 该方法认为能量损失是常数, 谱线上任意一点由非弹性散射电子引起的背景, 只来源于具有更高动能的电子的散射, 正比于具有更高动能的光电子谱峰积分强度, 所以任一能量位置的本底都正比于光电子能谱中具有较高能量的电子的总数目。 其计算公式如式(2)— 式(4)所示
式(2)、 式(3)和式(4)中, P+Q为扣除背景后峰的总面积, Q为动能在E以上的光电子信号的积分强度, I(x)为测量信号强度, B(x)为背景。 因为背景B(x)是未知的待求量, 开始无法计算面积P和Q, 为此首先用常数背景B1作为初值, 计算出P、 Q后再计算出新的背景, 如B2, 如此反复迭代, 直至收敛为止。
Tougaard方法扣除背景的理论基于这样一个事实: XPS中的峰形依赖于固体表面几个纳米深度中的结构, 这是因为光电子在固体内穿行的距离不同造成能量损失的不同, 从而影响峰形。 因此谱峰的峰形依赖于光电子激发处的深度。 通过对峰形的分析就可以推断固体表面几个纳米深度内的结构。 峰形随表面形态会发生显著的变化, 其原因是电子在逃离出固体时损失了能量。 它们穿越的路程越长, 损失的能量就越多。 对于只在固体中通过很短距离的光电子来说, 损失能量的机会少, 并且能量强度分布的改变也小。 对于在固体中通过很长距离的光电子来说, 能量损失的部分很大, 并且谱峰的能量强度降低得也多。 具体的计算公式如式(5)所示
式(5)中, La是衰减长度, θ 是电子出射方向与表面法线之间的夹角, λ 是电子非弹性散射平均自由程。 参数B和C用实验数据拟合, B=2 866 eV2, C=1 643 eV2, 可用于大多数金属及其氧化物和合金。
Shirley方法扣除背景有明确的物理意义, 即光电子谱峰下面的背景由动能大的光电子经散射损失能量后形成的。 这个方法的物理概念明确, 定量分析时峰面积计算误差较小, 重复性也好, 特别适合分峰, 但是其拟合的能量范围较小, 而且没有充分利用背景信号。 背景信号是光电子损失能量后形成的, 而能量损失的机制、 大小等却是与电子的能量、 具体样品的成分、 结构、 形貌等因素有关, 也就是说, 背景信号尽管变化不大, 但是其中却包含了许多与样品有关的信息。 原理上说, Tougaard方法扣除背景的物理思想与Shirley方法大致相同, 即背景信号是由动能大于该背景处能量值的光电子产生的。 但是与Shirley方法不同的是, Tougaard方法的背景范围要大得多, 它拟合的是从光电子峰高动能端到比光电子峰的能量小几十甚至几百eV范围内的背景信号。
XPS光电子谱峰有4个基本要素, 即谱峰分裂间距、 分裂谱峰强度、 谱峰的形状和对称性, 还有谱峰的半高峰宽(full width at half maxima, FWHM)。 在XPS谱峰拟合中, 拟合参数的设置至关重要, 就是对上述4个要素给出一个合适的约束条件, 以使得拟合结果具有合理的物理和化学意义。 下面分别概述这4个要素的参数设置。
通常XPS谱峰的结合能数值与元素的化学状态是密切相关的, 谱峰的强度与元素在样品中的含量密切相关, 这也是XPS可以进行定性定量分析的理论基础。 这里讨论的拟合参数并不涉及这两个方面, 因为这两个要素是未知的, 是与测试样品一一对应的, 也正是需要通过XPS测试来获取的信息。 在XPS谱峰拟合过程中设置拟合参数时, 实际上针对的是自旋轨道分裂所导致的谱峰要素。 自旋轨道分裂是一初态效应, 对于具有轨道角动量的轨道电子, 将会发生自旋磁场与轨道角动量的耦合, 从而发生能级分裂现象。 一般情况下, s轨道无自旋轨道分裂, 在XPS测试中呈现单峰; p, d, f轨道是自旋轨道分裂的, 在XPS测试中呈现双峰, 这个双峰结构就有谱峰分裂间距和分裂谱峰强度这两个要素, 在进行谱峰拟合时需要对这两个要素进行合理的设置和约束。
对于不同元素的光电子信号来说, 自旋轨道分裂引起的双峰, 其分裂间距是不一样的; 同一元素的不同轨道所对应的光电子信号, 其双峰的分裂间距也是不一样的。 各个元素自旋轨道分裂间距的数值在XPS数据手册中可以查询。 需要特别说明的是, 自旋轨道分裂的谱峰间距并不是固定不变的。 光电子主峰的谱峰间距随着元素化学态的改变而发生变化, 特别是第四周期元素的主峰2p双峰裂距随化学态发生明显变化, 例如Ti元素, 金属态物种的Ti(2p)双峰裂距为6.17 eV, 而TiO2的Ti(2p)双峰裂距为5.54 eV。 在进行XPS谱峰拟合时, 先对表面物种做一个大致的判断和归属, 根据这个归属来确定谱峰分裂间距的具体数值。 刘芬等[5]曾经对自旋轨道分裂间距进行了详细的整理。 如果没有相应的数值, 则在谱峰拟合过程中, 对谱峰分裂间距这一要素适当放宽条件, 允许其在一个设定的小范围内上下浮动, 从而适配真实的表面物种特征。
对于自旋轨道分裂后的谱峰强度, 高结合能处的谱峰强度小于低结合能处的谱峰强度。 理论上, p轨道的分裂双峰强度比为1∶ 2, d轨道的分裂双峰强度比为2∶ 3, f轨道的分裂双峰强度比为3∶ 4。 在进行XPS谱峰拟合时, 需要将自旋轨道分裂所导致的双峰做一个谱峰强度上的关联和约束, 以满足理论上的分裂双峰强度比例关系。
XPS测试技术是基于光电效应发展出来的一种检测方法, 入射X射线光子与样品中的原子发生相互作用, 使原子发生光电离, 释放出带有该原子特征信息的光电子, 经电子能谱仪系统收集、 检测、 记录和分析这些特征信号电子的能量分布和空间分布, 即得到XPS测试数据。 这些过程在XPS谱峰形状上都有所体现。 在X射线光电子能谱技术的理论中, 原子轨道中电子运动的自然线形通常认为是呈洛伦兹线形, 这是由光电离后激发态的寿命所产生的; 入射的单色化X射线激发源和电子能谱仪的分析检测系统对XPS谱峰的贡献是呈高斯线形。 另外, 热激发过程、 测试对象的不均匀性也会造成XPS谱峰的高斯型展宽。 所以实际得到的XPS谱峰是一个由洛伦兹和高斯混合而成的混合线形[6, 7, 8, 9]。 在XPS谱峰拟合中, 采用洛伦兹函数与高斯函数的组合来描述XPS测试数据的谱峰线形。
通常使用下列这几种函数来描述XPS测试数据的谱峰线形, 如洛伦兹函数L(x, F, E, h), 高斯函数G(x, F, E, h), 高斯-洛伦兹的和函数GLS(x, F, E, m, h)、 积函数GLP(x, F, E, m, h)和卷积函数Voigt, 它们的数学表达式分别如式(6)— 式(10)所示[6, 7, 8]。 式(6)— 式(10)中, x是变量, F是函数线的半高峰宽, E是函数线的峰顶能量数值, h是函数线的峰高值, m是洛伦兹线形在组合函数中所占的比例。 从它们的数学表达式可以看出, 这些函数的线形都是对称的。
理论上, XPS光电子谱的强度分布都同时含有高斯型和洛伦兹型的特征, 所以在数学处理上, 采用Voigt函数来进行XPS谱峰拟合是最合适的。 但采用Voigt函数拟合的计算量比较大, 因此发展了两种计算量相对简单的函数近似来代替真实谱峰中的Voigt线形, 分别是GLS(x, F, E, m, h)与GLP(x, F, E, m, h)[7, 8]。 就拟合效果而言, 有人认为采用高斯-洛伦兹和函数的效果较好[7], 有人认为采用高斯-洛伦兹积函数的效果较好[10]。 以本作者多年来在XPS谱峰拟合处理中对线形函数的实践体验来说, 积函数的拟合效果比和函数的拟合效果要好。 在某些具体案例中, 如果采用高斯-洛伦兹的积函数得不到好的拟合效果时, 可以再采用高斯-洛伦兹的卷积函数Voigt来进行谱峰拟合。
大多数的XPS谱峰基本上都是对称线形, 因此以上描述的对称函数是完全适用的。 但在实测的XPS谱图中, 经常会出现不对称的谱峰线形, 这是由于在费米能级处有较高的电子态密度, 产生了多电子激发而在高结合能端出现了谱峰的不对称拖尾。 如果费米能级处的态密度越高, 不对称拖尾就更加明显。 例如, 金属态Au在费米能级处的电子态密度较低, 其4f光电子谱峰比较对称; 而金属态Pt在费米能级处的电子态密度较高, 其4f光电子谱峰则表现出明显的不对称特征。 如果在分析有金属态Pt物种存在, 或者其他的在费米能级处有较高电子态密度的样品时, 就要考虑用不对称线形来进行XPS谱峰拟合。
对于简单的不对称峰形谱, 可引入拖尾函数来开展拟合工作。 具体的拖尾函数如式(11)和式(12)所示
式(11)和式(12)中, CTH为常数尾高比, TM为尾混合比, ET为指数尾比, DX是离开峰中心的距离。 通过调节拖尾的指数和拖尾的高度, 就可以在对称线形的基础上得到不同拖尾程度的谱线形状。
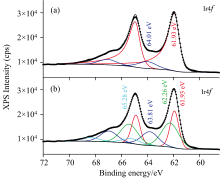
图2示出了某负载型催化剂样品的Ir(4f)谱峰, 在高结合能端出现明显的拖尾现象。 用拖尾函数进行谱峰拟合处理时, 得到两组不同化学状态的表面组分, 如图2(a)所示, 拟合结果表明样品中存在着两种不同化学状态的Ir物种, 分别表现出不同的Ir(4f)7/2谱峰结合能数值。 如果不用拖尾函数来进行处理, 仅仅用简单的对称线形函数来进行谱峰拟合处理, 则需要添加三到四组Ir(4f)组分, 才能使拟合后的总包络线与实测的实验谱线相吻合, 如图2(b)所示。 但是, 这样得到的拟合结果就表明在样品中存在着多种不同化学状态的Ir物种, 甚至有表面物种的Ir(4f)7/2谱峰结合能数值明显超出了正常范围, 并不具有一个合理的物理化学意义。 于是, 应用对称线形函数的拟合结果就会得到一个错误的数据分析。
在进行XPS谱峰拟合时, 需要设置的最后一个要素是谱峰的半高峰宽。 光电子谱峰信号的谱线宽度来自于四个方面的贡献, 分别是样品元素本质信号的自然宽度Γ 、 入射X射线激发源的自然线宽、 电子能谱仪系统的采谱条件, 以及样品自身状况的宽化因素等。
原子的不同轨道发生光电离后, 形成的芯空穴激发态具有不同的寿命, 因此不同元素的光电子主峰的本质信号自然宽度是不同的, 同种元素不同轨道发射出的光电子信号本身的自然宽度也是不同的。 对于给定元素, 通常内壳层轨道的Γ 值大于外壳层轨道, 这是因为内壳层芯空穴可被外壳层电子填充。 因此, 轨道越深, 芯空穴寿命越短, 本征峰宽越大。 例如, Au的本征峰宽按4f< 4d< 4p< 4s的顺序增大, 即谱峰结合能数值增大的次序。 同样, 给定轨道的Γ 值随着元素原子序数的增加而增大, 这是因为价电子密度(亦即填充芯空穴的概率)随着原子序数的增加而增大。
不同入射X射线激发源的自然线宽是不一样的。 常规双阳极靶Mg Kα 射线的自然线宽是0.70 eV, Al Kα 射线的自然线宽是0.85 eV, 经过单色化处理后Al Kα 射线的自然线宽降到了约0.25 eV。 如今商品化能谱仪系统也推出了高激发能量的金属阳极靶, 如单色化的Cr Kα 射线和Ag Lα 射线。 另外, 也可以申请机时用同步辐射光源来作为光电子能谱的入射激发源。 不同的激发光源具有不同的自然线宽, 对最终谱图峰宽的贡献也是不一样的。 在进行XPS谱峰拟合时, 需要结合实际使用的入射激发源来设置合理的谱峰FWHM值。
能谱仪系统在采集XPS数据时使用的采谱条件对谱峰宽度也有影响, 通常表现在通过能(pass energy)参数的设置上, 大的通过能可以得到较高的灵敏度, 但会降低谱峰的分辨率, 带来较大的谱峰FWHM值。 在处理测试数据或者阅读文献时, 需要注意所使用的能谱仪型号和信号采集的实验条件。
考虑到上述的影响因素, 实测的光电子谱峰信号的半高峰宽可以用一个简单数学关系式来表示
$\mathrm{FWHM}_{\text {total }}=\sqrt{\mathrm{FWHM}_{N}^{2}+\mathrm{FWHM}_{X}^{2}+\mathrm{FWHM}_{A}^{2}}$ (13)
式(13)中, FWHMtotal是实测光电子谱峰的总半高峰宽, FWHMN、 FWHMX、 FWHMA分别表示芯空穴寿命、 入射X射线激发源、 能谱仪采谱条件所贡献的半高峰宽。 需要说明的是, 这个关系式中没有考虑荷电效应和各种终态效应所引起的谱线增宽, 也没有考虑样品自身状况的差异所带来的谱峰宽化因素。 实际上, 现在测试的样品大多数都是纳米粉末材料, 颗粒粗糙和表面粗糙度会明显增加XPS谱峰线宽。 表面采样区域内与信息深度范围内各单层间的微分荷电也会使XPS谱峰出现宽化现象。 在对实际样品的XPS测试数据进行谱峰拟合处理时, 组分的半高峰宽要设置得更大一些, 一般要明显大于能谱仪系统验收时在金属标准样品上的技术指标。
上面详细阐述了XPS谱峰的4个基本要素, 即谱峰分裂间距、 分裂谱峰强度、 谱峰的形状和对称性、 谱峰的半高峰宽。 在设置拟合参数时应该注意和考虑下列这些因素: 子峰的个数依赖于谱线轮廓和可能的化学环境, 各个子峰应该有合理的物理化学意义; 合理的半高峰宽值, 一般情况下光电子主峰的半高峰宽在0.5~2.0 eV之间, 具体还跟测试时电子能谱仪系统的采谱条件有关; 合理的洛伦兹/高斯比, 一般情况下在0.25~0.35之间; 对自旋轨道分裂的双峰还需特别考虑, 两个峰之间的合理分裂间距和强度比。 对这几个参数设置合理的约束条件后, 就可以进行谱峰拟合处理了。
XPS谱峰拟合的第一条原则是, 拟合后的总包络线与原始谱线尽量吻合。 更重要的是, 拟合后的分谱有合理的半高峰宽和对应合理物理化学意义的结合能数值。 不能为了满足第一条拟合原则, 在拟合过程中添加多个分谱, 这样虽然拟合后的总包络线能够与原始谱线吻合得非常好, 但这些分谱并没有合理的物理化学意义, 纯粹是为了拟合而硬添加上去的。
另外, 全谱分析是很有必要的, 能够对谱峰信号做出正确的判断和归属, 防止出现错误的谱峰指认。 一般在进行XPS谱峰拟合时, 先由全谱扫描分析样品中存在的所有元素, 需要拟合的谱峰是否有其他元素光电子信号的干扰, 根据谱峰的相对强度来判断这个干扰的严重程度。 对谱峰有一个全貌的了解后, 再进行本底扣除和谱峰拟合的操作。 图3示出了某样品的全谱扫描及其Pb(4f)区域内的精细谱扫描数据。 由图3(b)可以明显看出, 该信号主要是由Pb(4f)自旋轨道分裂信号所贡献的。 仔细对比两个组分的谱峰形状, 低结合能端的谱峰信号明显与高结合能端的谱峰信号形状不一致, 说明在低结合能端的谱峰信号区域内可能存在着其他元素光电子信号的强度贡献。 如果简单地把这个谱峰归属为Pb物种的4f光电子信号, 那么得到的定量计算结果就存在着偏差。 对图3(a)中的全谱扫描进行物种归属, 发现样品中含有大量的Sn元素。 Sn的4s光电子信号落在Pb(4f)信号能量区域内, 对这个区域的谱峰信号有较大的贡献。 在进行元素的定性定量分析时, 就需要通过谱峰拟合处理将Sn元素的4s信号刨除掉, 从而得到准确的Pb(4f)光电子谱峰信号。
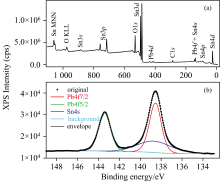 | 图3 某样品的(a) XPS全谱信号和(b) Pb(4f)能量区域内的精细谱拟合结果Fig.3 (a) XPS survey spectrum, and (b) the peak fitting results in the Pb(4f) region of a sample |
某些纯金属及其氧化物由于存在震激和多重分裂等多种终态效应, 其峰形并非是简单的高斯-洛仑兹线形, 而是非常复杂和难以拟合的不对称峰形, 会出现明显的谱峰劈裂现象, 可能还存在着很强的震激伴峰。 对于这些复杂峰形的情况, 用简单的线形来拟合, 拟合效果并不会好。 比如混合价态的铈氧化物样品, 如果用常规的方法对Ce(3d)信号进行谱峰拟合, 各分谱之间的拟合参数就很难给出明确的关联和约束, 拟合结果会存在非常大的不确定性。 在这种情况下, 可以考虑用非线性最小二乘法来进行拟合[11]。 以标准样品的谱图为参考谱, 非线性最小二乘法是调节参考谱的峰位置和强度, 而不改变其形状, 使得拟合后的总包络线与实测谱的方差最小。
可以使用XPSPeak软件或CasaXPS软件来进行XPS谱峰拟合处理, 这两个软件中已经预设了部分的参数设置建议; 也可以直接在Origin软件中做谱峰拟合处理, 此时就需要将相互之间有关联的拟合参数做一定的关联和约束。 当然, 各个电子能谱仪系统都有相应的软件程序, 可以进行光电子信号采集和后续的数据处理, 在XPS谱峰拟合操作上的功能更加强大。 运用软件程序对测试数据进行拟合处理, 经过多次迭代计算, 直至代表拟合偏差程度的卡方值基本保持不变, 一般卡方数值在5以内即认为拟合效果是不错的。
需要注意的是, 从数学运算上讲, XPS谱峰拟合可以有无穷多个解, 并不是只给出唯一的一个解, 但各分谱都具有物理和化学意义的解应该是唯一的, 该拟合结果才真正反映了样品中元素的化学状态。 在谱峰拟合过程中, 对拟合参数做一定的关联和约束, 并不断调整优化拟合参数, 以使得拟合结果具备一定的物理和化学意义。
下面通过一个具体的样品数据实例来展示谱峰拟合的详细过程。 图4示出了一个碳材料负载样品的XPS全谱和精细谱。 先由全谱扫描对样品做一个定性分析。 从XPS全谱数据可以看到, 除了C和O元素外, 还出现了S元素、 Mo元素、 N元素的光电发射信号。 根据XPS标准数据手册, 全谱中所有的光电子信号都做了相应的归属, 具体见图4(a)中的标识。 其中, 图4(b)中178~160 eV区域内的信号主要是S(2p)谱峰信号, 没有其他元素光电子信号的干扰; 图4(c)中Mo(3d)谱峰信号落在243~224 eV区域内, 但这一区域内还有S(2s)光电子信号的贡献; 同样的, 在图4(d)中410~389 eV区域内, 除了N(1s)谱峰信号的贡献外, 还有Mo(3p)3/2光电子信号的贡献。 如果要进一步对样品数据进行分析, 就需要进行XPS谱峰拟合, 将这些有干扰的谱峰信号分离出去, 从而得到精确的表面物种的光电子谱峰结合能数值与相对含量, 获得样品准确的定性定量分析结果。
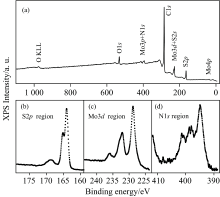 | 图4 某碳材料负载样品的(a) XPS全谱和(b) S(2p), (c) Mo(3d), (d) N(1s)能量区域内的精细谱Fig.4 (a) XPS survey spectrum, and the detailed spectra in the (b) S(2p), (c) Mo(3d), (d) N(1s) regions of a carbon-supported sample |
在本样品实例中, 所涉及到的光电子信号都是常规的谱峰形状, 峰形较为对称, 没有高结合能端的拖尾现象, 采用高斯-洛伦兹的积函数线形来进行谱峰拟合处理。 各分谱的洛伦兹/高斯比固定在0.30。 对于S(2p)、 Mo(3d)和N(1s)光电子主峰信号, 结合本样品测试时的采谱条件, 谱峰的半高峰宽设置为1.0~1.7 eV之间。 对于S(2p)谱峰, 自旋轨道分裂后双峰的裂分间距设置为1.18 eV, 强度比例为0.511, 两者的半高峰宽数值一致; 对于Mo(3d)谱峰, 自旋轨道分裂后双峰的裂分间距设置为3.13 eV, 强度比例为0.69, 两者的半高峰宽数值也一致。 图5示出了这三个能量区域内谱峰信号的拟合结果。
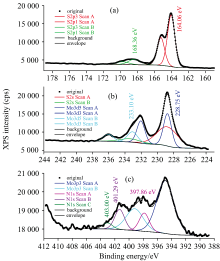 | 图5 某碳材料负载样品在(a) S(2p), (b) Mo(3d), (c) N(1s)能量区域内的XPS谱峰拟合结果Fig.5 The XPS peak fitting results in the (a) S(2p), (b) Mo(3d), (c) N(1s) regions of a carbon-supported sample |
S(2p)谱峰信号比较纯粹, 没有其他元素的光电子信号干扰。 178~160 eV区域内信号的拟合结果见图5(a)。 从拟合结果可知, 样品中存在着两种不同化学状态的S物种, 它们的谱峰结合能相差4.30 eV, 谱峰的强度之比为0.165。
既然在样品中检测到了S(2p)光电子信号, 相应地, S(2s)光电子信号也应该被检测到。 对243~224 eV区域内信号进行谱峰拟合处理时, 首先添加两个S(2s)光电子谱峰, 这两个谱峰的结合能位置间距和相对强度比由前面S(2p)谱峰的拟合结果得到。 按照化学位移的原子势能模型, 对于给定价壳层结构的原子, 所有内层电子结合能的位移几乎相同。 因此由S(2p)谱峰的结合能位移值来设置S(2s)光电子信号的结合能位移。 S(2s)轨道的结合能数值要大于S(2p)轨道, 其芯空穴的本征峰宽更大, 所以将S(2s)光电子信号的半高峰宽设置为2.5~3.5 eV之间。 然后再添加两组Mo(3d)谱峰信号, 就可以得到很好的拟合结果, 见图5(b)。 从拟合结果可知, 样品中存在着两种不同化学状态的钼物种, 它们的谱峰结合能相差4.35 eV, 谱峰的强度之比为0.385。
继续对410~389 eV区域内的信号进行拟合处理。 样品中既然检测到了Mo(3d)光电子信号, 相应地, Mo(3p)光电子信号也应该被检测到。 首先添加两个Mo(3p)3/2光电子谱峰, 依照同样的原则, 这两个谱峰的结合能位置间距和相对强度比由前面Mo(3d)谱峰的拟合结果得到。 这两个Mo(3p)3/2光电子信号的半高峰宽也要设置得相对宽一些, 本样品实例中将Mo(3p)3/2光电子信号的半高峰宽设置为2.5~3.5 eV之间。 然后再根据拟合的实际需要添加N(1s)组分, 使得拟合后的总包络线与原始谱线尽量吻合, 此时需要添加三个N(1s)组分才能得到比较满意的拟合结果, 见图5(c)。
经过上面描述的XPS谱峰拟合操作, 排除了样品中各个元素之间的光电子信号相互重叠的干扰, 可以得到样品中表面物种精确的谱峰结合能位置及其信号强度, 有利于物种的归属和化学态分析, 从而能够深入理解样品的元素组成、 表面物种类别及其相对含量与物理化学性质之间的构效关系。
在进行谱峰拟合时, 需要合理地限定XPS光电子谱峰这4个基本要素的取值范围, 运用软件就可以对XPS谱峰信号进行拟合分析了。 如果最后得到的拟合效果不理想, 可能有下面这几个因素, 即, 添加的谱峰类型不正确, 添加的谱峰数量不正确, 对上述拟合参数的约束条件不正确。 这些都需要不断进行调整优化, 以使得拟合后的总包络线与原始谱线尽量吻合, 并且各分谱都具有明确的物理化学意义。
在实际样品的XPS测试分析过程中, 通常存在着元素的光电子信号相互干扰的问题, 给XPS的定性定量分析带来了很大的困扰。 而XPS谱峰拟合是一个很好的解决此类问题的方法, 能够有效地消除光电子信号干扰的问题, 可以给出样品中各元素的准确相对含量和精确化学状态信息, 为后续的科研工作提供清晰的测试结果。 在谱峰拟合过程中, 需要对光电子信号的4个基本要素(自旋轨道分裂间距、 分裂谱峰强度、 谱峰的形状和对称性、 谱峰的半高峰宽)做一个合理的关联与约束, 在获得满意拟合效果的基础上, 各分谱都具有明确的物理化学意义, 由此反映出样品中元素真实的化学状态。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|