本研究所使用的三种不同类型土壤分别为栗钙土、 盐碱土和黄土, 对应于GSS-2、 GSS-18、 GSS-25三个土壤标准样品, 均购自于中国地质科学院地球物理地球化学勘查研究所。 三种不同用途土壤分别为采自于天津北辰工业区、 武汉市洪山区某建筑工程场地、 合肥市科学岛的工业用土、 建筑用土和农用土。

将九水硝酸铬[Cr(NO₃)₃· 9H₂O]、 硝酸铅[Pb(NO₃)₂]及四水硝酸镉 [Cd(NO₃)₂· 4H₂O](均为分析纯, 购于天津市光复精细化工研究所)分别溶于去离子水中配制成浓度为1 000 mg· L^-1的重金属Cr、 Pb、 Cd储备液。 将不同体积的Cr、 Pb、 Cd储备液分别加入到不同类型与不同用途土壤中充分搅拌, 再将土壤样品烘干研磨后过100目标准土壤检验筛, 每份土壤样品称取3 g, 于8 MPa压力下保压3 min制成厚度为2 mm直径为30 mm的薄片式土壤样品用于XRF光谱测量, 并采用iCAP RQ型电感耦合等离子体-质谱仪(ICP-MS, Thermo Fisher Scientific, 美国)测量每份土壤中重金属Cr、 Pb、 Cd的真实含量值。

XRF光谱测量所用仪器为Amptek公司的能量色散XRF光谱分析仪, 其激发源为配有Ag靶的Mini-X型X射线管, 探测器为硅漂移探测器(SDD), 光谱测量时相关参数设置为: 激发电压40 kV、 激发电流20 μ A、 信号累积时间120 s、 脉冲整形峰值时间6.4 μ s, 脉冲整形宽度0.8 μ s, 增益47.47。

1.3.1 极值法峰谷识别

由于土壤XRF光谱峰谷点是背景基线拟合的重要依据, 又是光谱中局部数据的极小值, 因此本文提出采用极值法对土壤XRF光谱的峰谷进行识别(peak valley identification based on extreme value, PIE)。 具体识别过程如下:

首先, 对相邻数据点间荧光强度的差值设置阈值δ , 对于一个数据点V_(i), 如果V_(i)< V_(i-1)、 V_(i)< V_(i+1)且max(V_(i-1), V_(i+1))- V_(i)> δ , 则V_(i)作为一个有效的峰谷点。 以该规则遍历光谱中每个数据点, 更新当前最小值。 如果当前点相对于最近的极小值变化超过了δ , 则标记为峰谷值, 并将此点设置为新的峰谷点, 从而实现XRF光谱中峰谷的识别。

1.3.2 惩罚项修正的三次平滑样条曲线拟合

平滑样条曲线拟合方法(spline)是一种基于样条曲线和平滑参数对一组数据进行拟合的方法, 它通过调整拟合曲线的平滑度来最佳匹配数据点。 由于三次样条具有较好的平滑特性和适中的计算复杂度, 因此本研究采用三次样条曲线对XRF光谱背景基线进行拟合。 设{X(i), Y(i), i=1, …, n}为一组XRF光谱上的特征峰谷点, 其中X(i)表示第i个峰谷点所在的通道数, Y(i)表示第i个峰谷点所对应的强度值, 则三次样条曲线的函数表达式定义为

Si(x)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3(1)

式(1)中, 每个S_i(x)对应于两个相邻数据点x_i和x_i+1之间的三次多项式段, a、 b、 c、 d为三次样条函数不同阶系数。

在采用极值法获得土壤XRF光谱一组峰谷点的基础上, 以这些点作为光谱背景的关键特征点进行三次样条插值拟合, 获得一条连接这些峰谷点的光滑曲线, 从而实现土壤XRF光谱背景基线的拟合。 但由于土壤XRF光谱中背景谱线强度随能量值的变化而改变, 不同能量区间处背景光谱强度具有较大差异性, 并且光谱在采集过程中会受到仪器和干扰信号噪声所影响, 导致基于三次样条曲线拟合方法所获得的背景谱线与真实背景间存在一定程度的偏差。 为了提高背景谱线拟合的准确性, 本研究在三次样条曲线函数中增加了平滑参数作为惩罚项对函数进行修正, 以权衡拟合曲线的平滑度和保真度。 添加平滑参数后的样条曲线函数如式(2)所示

$S(s)=\sum_{i=1}^{n}\left[y_{i}-S\left(x_{i}\right)\right]^{2}+\lambda \int_{x_{1}}^{x_{n}}\left[S^{\prime \prime}(x)\right]^{2} \mathrm{~d} x$(2)

式(2)中, 第一项表示样条曲线与数据点之间的残差平方和, 第二项表示曲线的光滑度约束, λ 为惩罚系数, S″为三次样条函数S(x)的二阶导函数。

1.3.3 基于PIEspline方法的土壤XRF光谱背景扣除流程

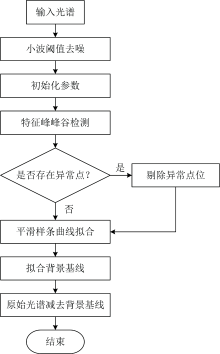
极值法峰谷识别(PIE)与惩罚项修正的三次平滑样条曲线拟合(spline)相结合所形成的PIEspline方法用于土壤XRF光谱背景扣除的具体流程如图1所示:

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 PIEspline背景扣除方法流程图Fig.1 Flowchart of the PIEspline background subtraction method

(1)输入土壤样品的原始XRF光谱Y;

(2)将光谱划分为低能量区域与高能量区域, 分别采用小波阈值去噪法对原始光谱进行平滑去噪处理, 小波基函数选取coif3, 低能量区域分解层数为3, 高能量区域分解层数为4;

(3)设置最优参数: 分别设置谱峰识别的阈值δ 、 谷点间的斜率阈值k及平滑参数λ ;

(4)遍历光谱数据中的每一个点, 如果当前点相对于最近的极小值变化率超过了δ , 则标记为峰谷点;

(5)依据峰谷点之间的标准差和斜率对点集合进行异常点检测, 剔除异常点位;

(6)将峰谷点集合代入式(2), 进行平滑样条曲线拟合, 计算出光谱背景谱线Z。

(7)将土壤样品的原始XRF光谱Y与计算出的光谱背景谱线Z相减, 获得土壤样品的净光谱N。

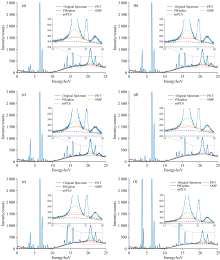
采用多重高斯峰叠加方法模拟含有多个特征峰且背景谱线符合真实土壤背景光谱变化趋势的XRF光谱, 以验证PIEspline方法性能。 所模拟的光滑与具有噪声的两种XRF光谱及PIEspline、 airPLS、 IWT、 SNIP四种方法所拟合的背景谱线如图2与图3所示。 可以看出, 无论是对于光滑的XRF光谱, 还是具有噪声的XRF光谱, 与airPLS、 IWT、 SNIP三种方法相比, PIEspline方法所拟合的背景谱线最接近于真实背景谱线, 在谱峰密集的低能量区域未出现背景谱线高估现象, 在谱峰稀疏的高能量区域也未出现背景谱线低估问题, 因此能够很好保留特征谱峰的位置和形状等光谱信息。 而airPLS和IWT方法对谱峰密集的低能量区域光谱背景拟合均出现了过拟合现象, IWT和SNIP方法对谱峰稀疏的高能量区域光谱背景拟合均出现了低估问题。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 模拟的土壤光滑XRF光谱及基于不同方法获得的背景谱线 (a): 模拟的光滑XRF光谱及基于PIEspline方法获得的背景谱线; (b): 基于不同方法获得的背景谱线Fig.2 Simulated smooth XRF spectrum of soil and background spectra obtained by different methods (a): Simulated smooth XRF spectrum and background spectrum obtained by PIEspline method; (b): Background spectra obtained by different methods

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 模拟含有噪声的土壤XRF光谱及基于不同方法获得的背景谱线 (a): 模拟含噪声的XRF光谱及基于PIEspline方法获得的背景谱线; (b): 基于不同方法获得的背景谱线Fig.3 Simulated XRF spectrum with noise of soil and background spectra obtained by different methods (a): Simulated XRF spectrum with noise and background spectrum obtained by PIEspline method; (b): Background spectra obtained by different methods

进一步对比四种方法运行速度及背景拟合结果的准确性, 结果如表1所示。 可以看出, 在最优参数下, 与airPLS、 IWT、 SNIP三种方法相比, PIEspline方法所拟合的背景谱线与真实背景谱线间的均方根误差(RMSE)分别为0.425 8和0.644 1, 均为最小值, 同时PIEspline方法在进行光谱背景扣除时运行时间分别为0.023和0.037 s, 均小于传统三种光谱背景扣除方法所用的运行时间。

表1

Table 1

表1(Table 1)

表1 四种方法在处理模拟光谱时的性能对比 Table 1 Comparison of performance of four methods in processing simulated spectra 方法 模拟的光滑光谱 模拟的含有噪声光谱 parameters Time/s RMSE parameters Time/s RMSE airPLS λ =105, p=0.05 0.082 0.965 2 λ =105, p=0.05 0.125 1.109 2 IWT Ψ =db4, J=8 0.078 3.845 1 Ψ =db4, J=8 0.316 3.919 2 SNIP m=22 0.041 1.268 3 m=22 0.097 1.473 8 PIEspline δ =1, λ =10-5 0.023 0.425 8 δ =1, λ =10-5 0.037 0.644 1

表1 四种方法在处理模拟光谱时的性能对比 Table 1 Comparison of performance of four methods in processing simulated spectra

由此可见, 对于模拟的土壤XRF光谱, 在所对比的PIEspline、 airPLS、 IWT、 SNIP四种方法中, 本研究所提出的PIEspline 方法用于背景扣除时具有最好的准确性及最优的运行效率。

2.2.1 光谱背景拟合准确性

分别选用栗钙土、 盐碱土和黄土三种不同类型土壤及农用土、 工业用土、 建筑用土三种不同用途土壤XRF光谱为研究对象, 进一步验证PIEspline方法对不同类型与不同用途实际土壤XRF光谱背景拟合的准确性。 PIEspline、 airPLS、 IWT、 SNIP四种方法对6种土壤XRF光谱的背景拟合结果如图4所示。 可以看出, 对于6种土壤XRF光谱, 在背景强度较高的18~25 keV和元素特征峰密集的5~10 keV范围内, airPLS和SNIP两种方法均存在不同程度的背景过拟合现象, IWT方法则存在背景低估现象; 且在0~5 keV的低能量范围内, 这三种方法均出现了背景低估问题; 而与airPls、 IWT、 SNIP三种方法相比, PIEspline方法均能精准拟合出6种土壤XRF光谱全谱的背景谱线, 在整个XRF光谱区域内均未出现背景过拟合及低估问题。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同土壤样品XRF光谱背景拟合效果图 (a): 栗钙土; (b): 盐碱土; (c): 黄土; (d): 农用土; (e): 工业用土; (f): 建筑用土Fig.4 Background fitting results of XRF spectra for different soil samples =(a): Chestnut soil; (b): Saline-alkali soil; (c): Loess; (d): Agricultural soil; (e): Industrial soil; (f): Construction soil

提取6个土壤样品原始XRF光谱中低、 中、 高不同能量处10个特征谷点(能量为: 1.65、 3.5、 4.37、 6.2、 8.5、 10.4、 13.15、 15.44、 17.84和22.5 keV)的荧光强度值, 将PIEspline、 airPLS、 IWT、 SNIP四种方法所拟合的背景谱线中相同谷点处的荧光强度与原始光谱中相应位置处的荧光强度对比, 计算10个点位荧光强度的平均相对误差, 结果如表2 所示。 可以看出, 除了栗钙土及工业用土PIEspline方法的平均相对误差接近于SNIP方法以外, 对于每一种类型及每一种用途土壤, PIEspline方法的平均相对误差均远小于airPLS、 IWT、 SNIP三种方法, 相比平均分别降低了84.88%、 76.30%和16.51%。

表2

Table 2

表2(Table 2)

表2 四种方法所拟合的背景光谱中10个谷点位置处荧光强度的平均相对误差(%) Table 2 Average relative errors (%) of fluorescence intensities at 10 valley positions in the background spectra fitted by four methods 栗钙土 盐碱土 黄土 农用土 工业用土 建筑用土 平均值 airPLS 61.51 67.76 61.29 85.66 84.08 70.97 71.88 IWT 48.83 42.87 47.69 50.88 45.30 39.67 45.87 SNIP 9.32 14.26 13.47 12.46 12.53 16.10 13.02 PIEspline 9.84 10.68 10.96 6.73 12.74 14.25 10.87

表2 四种方法所拟合的背景光谱中10个谷点位置处荧光强度的平均相对误差(%) Table 2 Average relative errors (%) of fluorescence intensities at 10 valley positions in the background spectra fitted by four methods

上述研究表明, 与airPLS、 IWT、 SNIP三种光谱背景扣除方法相比, PIEspline方法能够更准确拟合出不同类型与不同用途土壤XRF光谱中的背景谱线。

2.2.2 重金属定量分析准确性

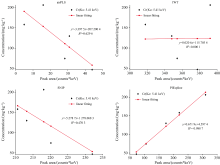
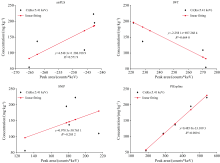
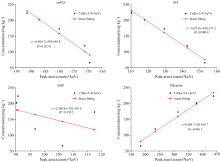
分别以XRF光谱中特征峰位于低、 中、 高三个能量区间内的重金属Cr(kα 为5.41 keV)、 Pb(Lα 为10.55 keV)、 Cd(Kα 为23.11 keV)为研究对象, 分析PIEspline、 airPLS、 IWT、 SNIP四种方法分别用于XRF光谱背景扣除时, 栗钙土、 盐碱土、 黄土三种不同类型土壤及农用土、 工业用土、 建筑用土三种不同用途土壤中Cr、 Pb、 Cd定量分析的准确性, 以评估PIEspline方法用于不同土壤多种重金属同时XRF检测的普适性。 在四种方法扣除光谱背景的基础上, 所建立的6种土壤中Cr、 Pb、 Cd定量分析曲线的线性相关系数(R²)如表3所示, 其中栗钙土、 盐碱土、 黄土中Cr的定量分析曲线如图5— 图7所示。

表3

Table 3

表3(Table 3)

表3 不同类型与不同用途土壤中Cr、 Pb、 Cd定量分析曲线的线性相关系数 Table 3 Linear correlation coefficients of quantitative analysis curves for Cr, Pb, and Cd in different types and different uses of soils 相关系数 Cr Pb Cd airPLS IWT SNIP PIEspline airPLS IWT SNIP PIEspline airPLS IWT SNIP PIEspline 栗钙土 0.629 6 / 0.470 3 0.988 7 0.983 2 0.946 6 0.916 9 0.997 8 0.999 7 0.977 5 0.966 2 0.995 6 盐碱土 0.579 1 0.664 0 0.205 2 0.989 6 0.955 5 0.966 7 0.985 2 0.978 6 0.994 0 0.983 8 0.784 5 0.995 3 黄土 0.927 0 0.980 9 0.170 2 0.963 1 0.992 4 0.981 5 0.995 2 0.986 7 0.985 1 0.932 3 0.927 3 0.980 4 农用土 0.962 3 0.963 8 0.973 1 0.994 2 0.995 2 0.995 9 0.996 6 0.996 2 0.992 4 0.994 4 0.949 0 0.991 7 工业土 0.910 2 0.910 0 0.918 2 0.983 6 0.955 9 0.962 5 0.971 1 0.968 2 0.989 0 0.990 0 0.972 6 0.992 6 建筑土 0.903 6 0.961 6 0.915 8 0.994 4 0.948 2 0.963 4 0.818 5 0.953 7 0.993 0 0.986 7 0.976 3 0.993 4

表3 不同类型与不同用途土壤中Cr、 Pb、 Cd定量分析曲线的线性相关系数 Table 3 Linear correlation coefficients of quantitative analysis curves for Cr, Pb, and Cd in different types and different uses of soils

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 栗钙土(GSS-2)中Cr的定量分析曲线Fig.5 Quantitative analysis curve of Cr in chestnut soil (GSS-2)

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 盐碱土(GSS-18)中Cr的定量分析曲线Fig.6 Quantitative analysis curve of Cr in saline-alkali soil (GSS-18)

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 黄土(GSS-25)中Cr的定量分析曲线Fig.7 Quantitative analysis curve of Cr in loess (GSS-25)

由图5— 图7可以看出, 对于栗钙土和黄土, 采用airPLS、 IWT、 SNIP三种方法扣除光谱背景后, Cr元素的Kα 特征谱峰净积分强度并不随Cr浓度的增加而增大, 即两者间并不呈正相关关系; 同样对于盐碱土, 基于IWT方法扣除光谱背景后, Cr的Kα 特征谱峰净积分强度与Cr浓度间也不呈正相关关系。 这一结果表明: airPLS、 IWT、 SNIP三种方法对栗钙土、 黄土及IWT方法对盐碱土XRF光谱中Cr特征峰处背景拟合时均存在过拟合情况, 说明airPLS、 IWT、 SNIP三种背景扣除方法对不同土壤中多种重金属同时XRF定量分析并不具有普适性。 而当采用PIEspline方法进行光谱背景扣除后, 6种土壤中Cr、 Pb、 Cd特征谱峰净积分强度与重金属浓度间都具有很好的正相关关系, 定量分析曲线R²均在0.953 7~0.997 8之间, 均接近甚至远高于其他三种背景扣除方法所对应的三种重金属定量分析曲线的R², 说明本研究所提出的PIEspline方法用于不同类型与不同用途土壤中多种重金属同时XRF定量分析时具有最好的普适性。

采用四种背景扣除方法分别对含有Cr、 Pb、 Cd的6种土壤XRF光谱进行背景扣除, 并利用表3中基于相应背景扣除方法所建立的6种土壤中Cr、 Pb、 Cd定量分析曲线反演三种重金属的含量值, 通过与ICP-MS所测得的重金属真实含量值对比, 根据相对误差分析不同背景扣除方法所获得的重金属定量分析准确性, 结果如表4所示。

表4

Table 4

表4(Table 4)

表4 不同类型与不同用途土壤中Cr、 Pb、 Cd定量分析的相对误差(%) Table 4 Relative errors (%) of quantitative analysis for Cr, Pb, and Cd in different types and different uses of soils 相对误差 Cr Pb Cd airPLS IWT SNIP PIEspline airPLS IWT SNIP PIEspline airPLS IWT SNIP PIEspline 栗钙土 20.51 3.24 5.33 3.64 10.64 17.12 22.95 2.70 0.35 14.30 15.78 3.81 盐碱土 55.68 20.30 64.69 2.43 20.23 10.74 17.53 0.56 11.39 14.68 83.77 6.58 黄土 15.41 5.35 37.91 7.02 3.73 4.84 4.25 2.69 12.63 23.53 10.24 9.52 农用土 19.04 17.40 13.18 0.63 10.64 9.54 5.12 4.33 8.42 9.86 50.83 9.00 工业土 12.55 17.68 13.29 8.88 6.53 7.27 7.45 2.11 4.61 6.74 12.24 1.86 建筑土 27.87 21.71 16.59 1.48 4.31 3.33 14.75 2.59 2.80 9.18 0.89 0.42 平均 25.18 14.28 25.17 4.01 9.35 8.81 12.01 2.50 6.70 13.05 28.96 5.20

表4 不同类型与不同用途土壤中Cr、 Pb、 Cd定量分析的相对误差(%) Table 4 Relative errors (%) of quantitative analysis for Cr, Pb, and Cd in different types and different uses of soils

可以看出, 当采用PIEspline方法对XRF光谱进行背景扣除时, 6种土壤中Cr、 Pb、 Cd定量分析的相对误差分别为0.63%~8.88%、 0.56%~4.33%、 0.42%~9.52%, 平均为4.01%、 2.50%、 5.20%, 与airPLS、 IWT、 SNIP三种方法相比有较大程度的降低, 平均分别降低了22.39%~84.07%、 60.15%~71.92%和79.18%~84.07%; 并且当土壤类型与用途发生改变时, 与airPLS、 IWT、 SNIP方法三种方法相比PIEspline方法相对误差波动最小, 表现出了最好的稳定性。 这些结果说明PEIspline方法用于不同土壤中多种重金属同时XRF定量分析时具有更好的准确性和普适性。

上述研究表明, 与airPLS、 IWT、 SNIP三种传统光谱背景扣除方法相比, 本研究所提出的PIEspline光谱背景扣除方法更适用于不同类型及不同用途土壤中多种重金属同时XRF定量检测, 能够保证低、 中、 高不同能量区间内重金属XRF定量分析均具有很好的准确性。