作者简介: 关力畅,女, 1993年生,公安部鉴定中心博士后,湖南警察学院刑事科学技术系讲师 e-mail: guanlichang@iccas.ac.cn
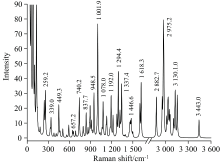
因芬氟拉明(fenfluramine)可抑制食欲, 不少商家非法将其添加在食物中进行售卖。 食用芬氟拉明后, 可引发肝脏功能异常、 瓣膜性心脏病、 原发性肺动脉高压等严重影响身体健康的疾病。 因此研究芬氟拉明分子的结构、 光谱、 分子激发等具有十分重要的实际意义。 基于密度泛函理论(DFT), 使用B3LYP泛函6-311++G(2d, 2p)基组, 对芬氟拉明分子进行结构优化。 在此基础上对该分子的结构、 前线轨道、 拉曼光谱、 静电势能和紫外光谱开展了一系列详细的研究。 获得了芬氟拉明分子的基本结构信息, 其最高占据分子轨道和最低未占据分子轨道均为alpha+beta型轨道, 能量分别为-6.25和-1.22 eV, 能级差为5.03 eV。 实验拉曼光谱中756.5和1 003.5 cm-1位置有两个强峰, 其中756.5 cm-1位置的强峰为CF3的对称变形振动和苯环上C═C的不对称变形振动; 1 003.5 cm-1位置的强峰为苯环上C═C的对称变形振动, 是间位双取代苯的特征谱带。 实验拉曼光谱和计算拉曼光谱的线性拟合方程为 y=0.988 x+10.328, R2=0.999, 呈现出较好的一致性。 文章还讨论了芬氟拉明分子的表面静电势能分布和激发态性质。 芬氟拉明分子共包含17个静电势能极大值点和12个静电势能极小值点。 在-0.01~0.025 a.u.能量区间静电势能的表面积分布较为均匀。 分子的紫外光谱主要由第1、 2、 3激发态决定, 其中第2激发态的贡献率高达82.516%。 利用空穴-电子分析法分析得出, S0→S1和S0→S2的激发类型均为胺基到苯环方向上的n-pi*电荷转移激发; S0→S3的激发类型是胺基到苯环方向的n-pi*电荷转移激发, 同时伴随胺基到附近碳链的n-σ*局域激发。 以上这些基础理论计算工作不仅为食品中非法添加芬氟拉明的检测提供了理论依据, 还为研究其衍生物提供理论基础。
Fenfluramine can inhibit appetite, so many merchants illegally added it to food for sale. After eating fenfluramine, it can cause liver dysfunction, valvular heart disease, primary pulmonary hypertension, and other diseases that seriously affect health. Therefore, studying fenfluramine molecules' structure, spectrum, and molecular excitation is of great practical significance. This work used the density functional theory (DFT) method with the B3LYP functional and 6-311++G(2d,2p) basis set for structural optimization. Furthermore, a series of studies were done on the structure, frontier orbits, Raman spectra, electrostatic potential, and UV spectra of the fenfluramine molecule. The basic structure information was obtained. The highest occupied orbital (HOMO) and the lowest unoccupied orbital (LUMO) were both alpha + beta orbits. The energy of HOMO, LUMO, and their energy gap was -6.25, -1.22 and 5.03 eV, respectively. There were two strong peaks at 756.5 and 1 003.5 cm-1 in the experimental Raman spectrum. The strong peak at 756.5 cm-1 was the symmetric deformation vibration of CF3 and the asymmetric deformation vibration of C═C on the benzene ring. The strong peak at 1 003. 5 cm-1 was the symmetrical deformation vibration of C═C on the benzene ring, the characteristic band of meta-disubstituted benzene. The linear fitting equation of experimental Raman spectra and calculated Raman spectra is y=0.988 x+10.328, R2=0.999, showing good consistency. This work also discussed the electrostatic potential and excited state properties of fenfluramine. The fenfluramine molecule contained 17 electrostatic potential energy maximum points and 12 electrostatic potential energy minimum points. The surface area distribution of electrostatic potential energy in the range of -0.01~0.025 a.u. was relatively uniform. The UV spectra were mainly determined by the first, second, and third excited states, and the contribution of the second excited state was as high as 82.516%. The electron excitation characteristics were studied by using hole-electron analysis. It could be found that S0→S1 and S0→S2 were attributed to the n-pi* charge-transfer excitation in the direction from the amino group to a benzene ring. S0→S3 was attributed to the superposition of the n-pi* charge-transfer excitation in the direction from amino group to benzene ring, and the n-σ* local excitation between ammonio to carbon chain nearby. These basic theoretical calculations provide a theoretical basis for not only the detection of illegally added fenfluramine in food but also the study of its derivatives.
芬氟拉明(fenfluramine)纯品为白色结晶性粉末, 无臭, 微苦。 分子式C12H16F3N, 分子结构如图1(a)所示, 分子量231.257。 芬氟拉明曾被批准用于治疗外源性肥胖症, 但随后有研究发现, 芬氟拉明在体内广泛代谢[1], 服用该药物的患者出现肝脏功能异常、 瓣膜性心脏病、 原发性肺动脉高压等疾病症状[2, 3]。 我国食品药品监督管理局于2009年要求停止盐酸芬氟拉明原料药和制剂在我国的生产、 销售和使用, 但依然有不少商家非法在食物中添加芬氟拉明并公开售卖。 值得注意的是, 近几年研究表明, 芬氟拉明在应对最难治疗的癫痫性脑病Dravet综合征和Lennox-Gastaut综合征上具有很好表现。 在Ⅲ 期临床试验中, 在基础治疗上添加芬氟拉明, 有效减少了癫痫发作频率, 提供了临床益处[4, 5, 6]。
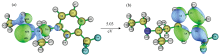
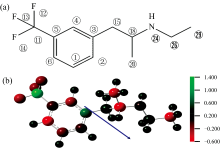 | 图1 芬氟拉明分子(a)结构式; (b)Mulliken电荷分布和偶极矩取向Fig.1 (a) The structural formula of fenfluramine; (b) The Mulliken charge distribution and dipole moment orientation of fenfluramine |
目前已有多种技术用于检测食品、 药品和人体血浆中芬氟拉明的含量, 如气相色谱-质谱法联用技术[7]、 高效液相色谱-质谱法联用技术[8]、 固相萃取-高效液相色谱串联质谱法[9]等。 这些方法虽然灵敏度高、 准确性好, 但是需要较为复杂的样品处理过程, 操作过程相对繁琐, 具有一定的局限性。 而光谱检验方法在测试时几乎无需特殊制样, 尤其是拉曼光谱具有指纹识别的特征, 在实际检测过程中可以发挥重要作用。 本文以目前已有的实验拉曼光谱[10]研究为基础, 使用密度泛函理论(DFT)对芬氟拉明的分子结构、 前线轨道、 拉曼光谱、 静电势能、 紫外光谱进行系统讨论, 为芬氟拉明分子的研究提供分子层面的解析, 为今后实验检测食品中非法添加芬氟拉明物质提供理论依据。
本文基于中国国家网格通用计算平台Gaussian09 E01[11]软件包, 使用密度泛函理论(DFT)中的B3LYP[12]泛函, 6-311++G(2d, 2p)[13, 14]基组, 先对芬氟拉明分子进行结构优化, 然后使用相同的泛函与基组进行拉曼光谱的计算。 图1(a)为芬氟拉明分子的结构式, 数字代表各原子的序号。 查看输出文件无虚频, 证明优化后的结构是可以稳定存在的。
经过计算, 苯环上的碳碳键长在1.39~1.40 Å 之间; 其余碳碳键长在1.50~1.56 Å 之间; C18-N24和N24-C26键长均为1.46 Å 。 C1-C2-C3、 C4-C5-C11、 C2-C3-C15、 C3-C15-C18、 C15-C18-N24、 C18-N24-C26的键角分别为121.2° 、 118.4° 、 120.6° 、 114.5° 、 113.8° 和117.1° 。 C3-C4-C5-C11、 C2-C3-C15-C18、 C18-N24-C26-C29二面角分别为-179.7° 、 -74.8° 和-175.9° 。 芬氟拉明分子主要的键长、 键角、 二面角的数值已列于表1中。 图1(b)表示了芬氟拉明分子Mulliken电荷的分布情况。 其中, 正电荷为绿色, 负电荷为红色, 不带电荷为黑色, 色调越明亮表示电荷越大。 C1、 C2、 C4、 C5、 C6、 F12、 F13、 F14、 C18、 C20、 N24、 C29原子带负电, 其余原子带正电, 原子所带电荷数如表2所示。 C11带最大正电荷1.337 e, C6带最大负电荷-0.589 e。 图1(b)中蓝色箭头为偶极矩的取向, 由三氟甲基一端指向侧链中的甲基。
| 表1 芬氟拉明分子优化后的主要几何参数 Table 1 The partially optimized geometric parameters of fenfluramine |
| 表2 芬氟拉明分子中的各原子Mulliken电荷分布以及对分子前线轨道的贡献 Table 2 The Mulliken charge distribution for each atom and the contribution to the frontier orbital of fenfluramine |
研究分子轨道中的最高占据分子轨道(highest occupied molecular orbital, HOMO)和最低未占据分子轨道(lowest unoccupied molecular orbital, LUMO)及其能级差, 对于研究分子的结构、 化学性质具有重要的意义, 因为HOMO、 LUMO和能极差能够决定分子的电子得失和转移能力[15, 16]。 芬氟拉明分子HOMO和LUMO均为alpha + beta型轨道, 其中HOMO能级为-6.25 eV, LUMO能级为-1.22 eV, HOMO-LUMO能级差为5.03 eV。 图2为芬氟拉明分子的HOMO、 LUMO电子云分布图。 HOMO主要集中在胺基上, 少部分集中在连接苯环的碳链上。 LUMO主要集中在苯环上, 少部分集中在连接苯环的甲基上。 无论是HOMO还是LUMO, 均在靠近原子核的部分轨道概率密度最高, 离核越远, 轨道概率密度越低。 在Multiwfn[17]软件中, 使用Mulliken[18]方法计算得到了芬氟拉明分子中C、 N、 F原子对HOMO和LUMO的贡献率, 相关数值列于表2中。
在Multiwfn软件[17]中输入实验入射光波长785 nm、 温度298.15 K、 频率校正因子0.963[19]后, 得到基于拉曼强度展宽计算出的拉曼光谱, 如图3所示。 郭焱等[10]在实验中观测到, 位于756.5 cm-1位置的强峰为CF3的对称变形振动和苯环上C═C的不对称变形振动; 1 003.5 cm-1位置的强峰为苯环上C═C的对称变形振动, 是间位双取代苯的特征谱带。 实验上观测到的谱峰对应的振动模式列于表3中。 把实验测得和理论计算得到的拉曼光谱数据进行线性回归拟合, 线性方程为y=0.988x+10.328, R2=0.999, 吻合良好, 证明使用B3LYP/6-311++G(2d, 2p)计算得到的数据具有可靠性。
| 表3 芬氟拉明拉曼光谱的理论和实验频率振动归属 Table 3 The theoretical frequency and experimental frequency vibration attributions of fenfluramine |
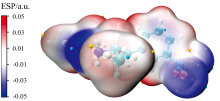
使用Multiwfn软件计算芬氟拉明分子的静电势能[17, 20, 21], 结合VMD[22]软件进行作图, 结果如图4所示。 静电势能图上蓝色代表负电, 红色代表正电, 带电区间为-0.05~0.05 a.u.。 黄色小球对应静电势能的极大值点, 青色小球对应静电势能的极小值点。 芬氟拉明分子共包含17个静电势能极大值点和12个静电势能极小值点。 从图4可以看出, 由于氟原子本身具有很强的电负性, 因此三氟甲基上的氟原子附近表现为蓝色的电负性区域, 静电势能极小值分别为-0.025、 -0.025和-0.024 a.u.。 由于甲基的电负性较弱, 因此在甲基附近表现为浅红色的电正性区域, 静电势能极大值分别为0.019、 0.030和0.011 a.u.。 苯环和亚甲基所在的位置为蓝色电负性区域和红色电正性区域的交界处, 表献为白色的电中性区域。 由于氮原子的电负性强于其周围的碳原子和氢原子, 因此在N24的局部范德华表面上出现静电势能的最小值-0.042 a.u., 在H25的局部范德华表面上出现静电势能的最大值0.043 a.u.。 以上芬氟拉明分子表面静电势能的信息为理解苯丙胺类衍生物的制备提供了理论基础。
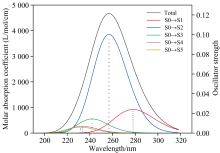
采用含时密度泛函理论方法(TD-DFT)计算了芬氟拉明分子的5个激发态, 图5为芬氟拉明分子的紫外吸收光谱及各激发态的贡献示意图。 横坐标为吸收波长, 左纵坐标为摩尔吸光系数, 右纵坐标为激发态的振子强度。 S0代表基态, Sx代表第x激发态。 根据计算结果可知, 光谱在256.868 4 nm处的吸收峰, S0→ S2贡献最大, 贡献率82.516%; S0→ S1, 贡献率8.503%; S0→ S3, 贡献率6.808%; S0→ S4, 贡献率1.293%; S0→ S5, 贡献率0.880%。 本文对S0跃迁到第1、 2、 3激发态这三种贡献率超过5%的跃迁进行讨论。
使用Multiwfn软件[17]对基于含时密度泛函理论方法计算得到的结果开展电子激发分析, 计算出了三个激发态中主要的轨道跃迁贡献率。 结果表明(仅列出贡献率大于5%的轨道跃迁), S0→ S1, 跃迁波长278.04 nm, 振子强度0.022 8, 激发能4.46 eV, 电子从第61号分子轨道(HOMO)向第62号分子轨道(LUMO)激发跃迁为主导, 跃迁贡献率为97.6%。 S0→ S2, 跃迁波长256.86 nm, 振子强度0.095 3, 激发能4.83 eV, 电子从第61号分子轨道向第63号分子轨道激发跃迁为主导, 跃迁贡献率为97.0%。 S0→ S3, 跃迁波长241.92 nm, 振子强度0.0137, 激发能5.13 eV, 电子从第61号分子轨道向第64号分子轨道激发跃迁为主导, 跃迁贡献率为85.2%, 电子从第61号分子轨道向第65号分子轨道激发跃迁贡献率为11.2%。
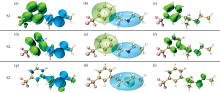
使用电子-空穴分析方法[21]具体分析芬氟拉明分子的电子激发特征。 图6为芬氟拉明分子的空穴-电子、 Chole-Cele、 Sr示意图。 空穴-电子、 Chole-Cele图中, 蓝色代表空穴, 绿色代表电子。 在图6(b)、 (e)和(h)中, 紫色小球和黑色小球分别代表了空穴和电子的质心位置。 Sr图中绿色的部分代表着空穴和电子在此处有显著交叠。 如图7(a)所示, 将芬氟拉明分子划分为6个片段, 激发态色彩刻度统一设置为0.0~1.0。 图7(b)、 (c)和(d)分别展现了芬氟拉明分子从S0跃迁到S1、 S2、 S3激发态过程中片段对空穴和电子激发贡献的热图。
 | 图6 芬氟拉明分子的空穴-电子、 Chole-Cele、 Sr示意图Fig.6 Electron-hole, Chole-Cele, and Sr distributions of fenfluramine |
 | 图7 芬氟拉明分子片段划分和片段对空穴和电子激发贡献的热图Fig.7 The divided six fragments of fenfluramine and contribution heat maps of each fragment to the hole and electron |
图6中S0到S1和S2激发态的6个图较为相似, 表4中的激发态参数也体现出了这一点。 S0→ S1和S0→ S2的空穴和电子的质心距离(D)分别为4.46和4.26 Å , 远大于C-C、 C-N键长, 空穴和电子质心距离较远, 因此导致库伦相互作用较弱, 分别为3.55和3.62 eV; Sr数值0.35和0.36 a.u., 空穴和电子分布重合的部分均相对较少[图6(b)、 (e)所示]; H指数2.20和2.24 Å , 反映空穴和电子的平均分布较广; t指数为正, 空穴和电子分布有明显分离。 结合以上参数综合判断, S0→ S1和S0→ S2类型归属于电荷转移激发。 根据图6(a)和(d)可知, 空穴主要由氮原子的孤对电子构成, 电子主要分布在苯环的pi* 轨道。 图7(b)和(c)表明绝大部分电子由胺基(片段5)转移至苯环(片段2)上。 结合图6(c)和(f)推测S0→ S1和S0→ S2均为胺基到苯环方向上的n-pi* 电荷转移激发。 虽然S0→ S1为HOMO到LUMO的激发跃迁, 但S0→ S2强度更强的原因在于, S2激发态空穴和电子的质心距离(D)更短、 分布重合度(Sr)更高、 分离度(t)更小, 库伦吸引能(Ecoul)更强。 因此芬氟拉明分子在256.868 4 nm处的紫外吸收峰以S0→ S2跃迁占据主导地位, 贡献率高达82.516%。
| 表4 芬氟拉明分子的激发态参数及空穴-电子库伦吸引能 Table 4 Excited state parameters and hole-electron Coulomb attractive energy of fenfluramine |
S0→ S3: 从表4可知空穴和电子的质心距离(D)为0.97 Å , 小于C— C、 C— N键长, 空穴和电子质心距离较近; Sr数值为0.32 a.u., 空穴和电子分布重合度相对较少[如图6(h)所示]; H指数3.00 Å , 反映空穴和电子的平均分布广度较广; t指数为负, 空穴和电子分离度较低。 因此虽然空穴和电子的质心距离较远, 但库伦相互作用依旧较强为4.32 eV。 结合以上参数综合判断, S0→ S3激发类型归属于电荷转移激发, 同时伴随局域激发。 空穴主要由氮原子的孤对电子构成, 电子分布主要由苯环上的pi* 轨道和碳链上的σ * 轨道构成。 图7(d)表明绝大多数电子从胺基(片段5)转移至苯环(片段2), 少部分电子在胺基(片段2)附近发生局域激发。 结合图6(i)推测S0→ S3激发是胺基到苯环方向的n-pi* 电荷转移激发, 同时伴随胺基附近碳链的n-σ * 局域激发。
采用密度泛函理论中的B3LYP[12]泛函, 6-311++G(2d, 2p)[13, 14]基组计算了芬氟拉明分子的基态结构、 拉曼光谱、 前线轨道、 紫外光谱与电子激发。 结果表明理论计算拉曼光谱与实验光谱吻合良好, 线性拟合方程为y=0.988x+10.328, R2=0.999, 并对拉曼光谱振动频率进行了详细的分析与指认。 芬氟拉明分子的HOMO和LUMO均为alpha+beta型轨道, 其中HOMO能级为-6.25 eV, LUMO能级为-1.22 eV, 能级差为5.03 eV。 在芬氟拉明分子的激发态光谱计算中, 对256.868 4 nm的吸收峰进行分析, 占据主要贡献的分别是S0→ S1、 S0→ S2和S0→ S3激发。 其中S0→ S1和S0→ S2为胺基到苯环方向上的n-pi* 电荷转移激发; S0→ S3为胺基到苯环方向的n-pi* 电荷转移激发, 同时伴随胺基到附近碳链的n-σ * 局域激发。 本文对芬氟拉明分子的结构及光谱进行了非常细致的研究, 为实验检测食品中非法添加芬氟拉明提供了理论依据, 为接下来深入研究苯丙胺类衍生物的性质提供参考。
致谢: 本文的计算结果是在中国国家网格(http://www.cngrid.org)/中国科学院超级计算环境(http://www.scgrid.cn)上得到的[23]。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|