假设组成游标的传感和参考干涉仪的自由光谱范围FSR分别为F_s和F_r, 可以推导出两个干涉仪并联后产生的叠加光谱包络的自由光谱范围F_o为

Fo=FsFr|Fs-Fr|(1)

当传感干涉仪的光谱随着被测量变化产生移动时, 包络也会产生偏移, 且移动量是传感干涉仪光谱移动的M倍

M=Fs|Fs-Fr|(2)

由式(1)、 式(2)可知, 传感和参考干涉仪的FSR越接近, 叠加光谱的包络的FSR就越大, 包络的移动量相对于传感干涉仪的光谱移动量的放大倍数也越高, 游标效应就越显著。

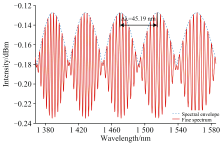
将两个FSR分别为4.08和3.78 nm的传感、 参考光纤干涉仪并联, 仿真获得并联结构的输出光谱如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 光学游标传感器输出光谱仿真图Fig.1 Optical vernier sensor output spectral simulation

图1中, 光谱包括“ 精细光谱” 和“ 包络光谱” 两部分的叠加。 其中包络的周期为~45.19 nm。 当其中传感干涉仪发生~2.0 nm的移动时, 光谱的包络移动范围为~27.2 nm, 包络移动幅度相比于传感干涉仪的光谱移动幅度放大了~13.6倍。 但当包络周期较长时, 由于受限于光源、 光谱仪有限的工作光谱范围, 利用传统的光谱测量法很难准确跟踪光谱包络完整的移动变化。 因此, 如何利用有限的光谱数据获得光谱包络移动信息的准确跟踪与观测, 显得尤为重要。

(1)LSTM网络

LSTM的核心是通过引入遗忘门、 输入门和输出门来控制细胞状态, 从而有效捕捉长时间序列特征之间的相关性, 通过将光谱包络波长上一波段特征信息传递给下一波段, 可有效掌握不同波段光谱包络序列特征^[20]。 其工作过程简述如下:

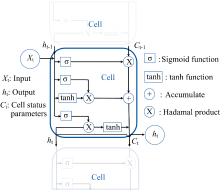
假设训练集时间序列数据为X_t(t=1, 2, …, N), LSTM网络模型则将会产生N个Cell单元, Cell结构运行过程如图2所示。 t时刻的输入样本X_t与上一时刻(t-1)的预测结果h_t-1作为t时刻输入值, 进入遗忘门, 其输出f_t为

ft=σ(Wf·[ht-1, xt]+bf))(3)

式(3)中: W_f为遗忘门的输出权重矩阵, b_f为偏置项。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 LSTM细胞结构图Fig.2 LSTM cell structure diagram

X_t同时输入输入门和输出门, W_i、 W_o分别为输入门和输出门的权重矩阵。 输入门i_t、 输出门o_t分别为

it=σ(Wi·[ht-1, xt]+bi))(4)

ot=σ(Wo·[ht-1, xt]+bo))(5)

式中, b_i、 b_o为偏置项。

最终, t时刻Cell单元的输出h_t由输出门o_t与Cell单元状态c_i共同决定, 即

ht=ottanh(ci)(6)

综上, 每个时刻Cell模型的输出h_t不仅作为当前时刻的预测值, 同时还对当前时刻Cell的状态C_t进行了记录, 并连同下一时刻(t+1)数据X_t+1作为下一个Cell的输入, 并对其进行训练。 如此持续下去, 直至N个时间序列数据训练并建立N个Cell, 这样就完成了一次训练过程。

目前常用的训练效果评估指标有: 决定系数(R²)、 均方根误差(RMSE)、 平均相对误差(MRE)以及平均绝对误差(MAE)等。 RMSE作为神经网络的典型损失函数, 不仅能定义网络性能, 还能间接表征LSTM预测数据的离散程度和稳定性, 因此采用RMSE作为评估指标, 其值越小说明预测越准确、 误差越小, RMSE的计算方法为

$E_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(P_{i}-T_{i}\right)^{2}}$(7)

式(7)中, T_i表示真实数据(即采集数据), P_i表示预测数据, N为光谱采样点, i为第i时刻光谱数据。

当RMSE指标达到预期值时停止训练, 否则适当增大训练次数直至RMSE达到预期值则训练结束。

(2)Bi-LSTM网络

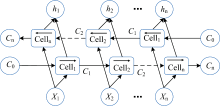
Bi-LSTM网络是LSTM网络的改进, 它由分别以正序和逆序输入的两个LSTM网络组合而成, 其输出向量为两个LSTM输出的拼接。 Bi-LSTM的结构模型如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Bi-LSTM的结构模型Fig.3 The structure model of Bi-LSTM

Bi-LSTM联合输出h_t公式如式(8)— 式(10)

h⃗t=LSTM⃗(h⃗t-1, xt, C⃗t-1), t∈[1, T](8)

h⃖t=LSTM⃖(h⃖t-1, xt, C⃖t-1), t∈[1, T](9)

ht=σ(Wo[h⃗t, h⃖t]+bh))(10)

式(8)— 式(10)中, h⃗t和 h⃖t分别表示双向LSTM层中正向层和后向层的隐藏输出序列, C⃗t和 C⃖t分别表示双向LSTM层中正向层和后向层的细胞状态。

相较于LSTM, Bi-LSTM可以同时正向和逆向地提取时间序列信息, 因此获得的特征数据同时拥有过去和将来的信息, 从而会对时间序列数据获得更准确的预测结果。

利用Bi-LSTM网络实现游标传感器输出光谱数据预测的过程如下:

(1) 网络构建: 设置Bi-LSTM层数, 每两层Bi-LSTM细胞单元数量等网络模型参数;

(2) 网络训练: 仿真生成不同特征的游标传感器光谱数据作为训练样本, 对Bi-LSTM网络进行训练。 设置初始训练次数, 当RMSE满足预期值时停止训练, 反之则适当增加训练次数直至满足需求。 若结果出现欠拟合或过拟合的情况, 则适当对Bi-LSTM层数及各层细胞单元数量进行相应增减;

(3) 光谱预测: 实际工作中, 采集传感器输出的光谱信号。 输入训练好的网络模型中, 利用训练获得的网络模型对其有限波长范围的输出光谱进行预测, 以获取更宽波长范围的光谱。

按1.3节所述过程, 首先构建网络模型: 本实验设置Bi-LSTM层数为六层, 每两层Bi-LSTM细胞单元数量分别为512、 256和128; 设置初始训练次数为8 000次; 初始学习率设置为0.005, 梯度下降算法为Adam算法。 模拟游标传感器光谱包络信号, 在MatLab软件上仿真生成具有不同包络周期的光谱数据训练, 包络周期的变化范围为10~40 nm、 周期变化的步长0.01 nm, 共生成3 000组数据。 为了提高模型的准确性和鲁棒性, 将这些数据打乱并作为训练集对Bi-LSTM网络进行训练, 以均方根误差RMSE作为网络训练的评估指标。 当RMSE< 0.001时可判断网络达到预期训练效果, 对网络停止训练, 否则调整训练次数, 继续训练网络。

(1)Bi-LSTM模型预测准确度的测试

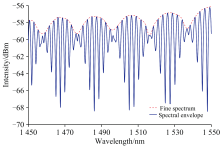
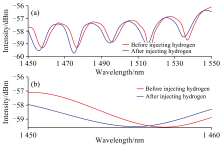
网络训练完成后, 就可利用网络进行实际光谱数据的预测。 为了验证Bi-LSTM网络在光学游标效应传感及解调技术的有效性, 制备了两个FSR值近似相等的F-P腔, 其中一个对氢气敏感, 另一个则对氢气不敏感, 其自由光谱范围F_s和F_r分别为2.34和2.64 nm, 两个F-P腔级联形成一组具有游标效应的传感器, 其输出光谱图如图4所示。 由式(2)及图4所示实测数据可知: 两个F-P腔氢气传感器形成游标传感器后, 光谱的包络周期近似为单个F-P腔FSR的8倍, 即在同样浓度氢气作用下, 游标光谱包络的波长移动范围相比单个F-P腔氢气传感器的波长移动范围放大了~8倍, 即实现了传感器8倍的增敏。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 初始光谱图Fig.4 Initial spectrogram

将传感器置于1%氢气浓度中, 采用超连续谱光源(光谱范围1 450~1 550 nm, 武汉安扬激光技术股份有限公司生产, 型号: SC-5)激励传感器, 获得传感器在注入氢气前后, 输出光谱的变化如图5(a)所示。 图中可见, 注入氢气后, 光谱发生了蓝移。 为验证Bi-LSTM网络的有效性, 从图5(a)中截取1 450~1 460 nm窄波长范围内氢气注入后的光谱数据, 对其低通滤波获得光谱包络后, 进行去除基线漂移和数据归一化预处理并送入训练好的Bi-LSTM网络中, 对1 460~1 550 nm波长范围的包络光谱数据进行预测, 预测结果进行反归一化、 中心线补偿等处理。 处理结果与原始光谱包络曲线对比显示在图6中。 从该图中可以看到, 预测的光谱包络曲线与原始光谱包络曲线具有很好的吻合性。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 注入氢气前后传感器输出光谱变化 (a): 采用超连续光源获得的传感器输出光谱; (b): 从(a)中截取1 450~1 550 nm部分的光谱Fig.5 Spectral changes of sensor output before and after hydrogen injection (a): Sensor output spectra obtained using a supercontinuum light source; (b): 1 450~1 550 nm band extracted from (a)

图6

Fig.6

	Figure Option ViewDownloadNew Window
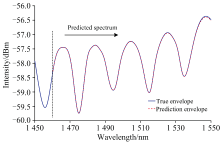	图6 Bi-LSTM网络对传感器光谱包络数据的预测Fig.6 Prediction of the spectral envelope data of the sensor by the Bi-LSTM network

进一步地, 提取图6中Bi-LSTM网络预测的光谱包络波峰值与实际光谱包络的波峰值并计算误差, 结果列于表1中。 由图6及表1可以看出:

表1

Table 1

表1(Table 1)

表1 包络光谱波峰值的预测误差 Table 1 Prediction error of envelope spectral wave peaks 预测波峰 波长/nm 与真实波长 差值/nm 波峰处幅值相对 误差/% 1 465.60 0.00 4.35× 10-3 1 483.48 0.00 5.75× 10-3 1 503.14 0.00 9.08× 10-3 1 523.52 0.00 0.020 1 544.74 -0.02 0.058

表1 包络光谱波峰值的预测误差 Table 1 Prediction error of envelope spectral wave peaks

① 在波长方面, 由Bi-LSTM网络预测的包络峰值波长与实际值误差极小, 只是随着预测数据序列的增长, 在第5个波峰(1 544.74 nm)处出现0.02 nm的误差; 在幅值方面, 随着预测数据序列的增长, 波峰处的幅值误差逐渐增大, 最大误差也同样出现在第5个波峰处, 但误差仅为0.058%。 实际中, 只要能够预测出大于1个包络周期的光谱数据, 就能够满足游标传感器的解调要求, 即解调过程中只关注峰值波长的预测误差, 幅值误差并不影响解调结果, 可以忽略;

② 由于游标传感器输出光谱中包络的变化幅度要远大于组成游标的单个传感器的光谱的变化幅度[见式(1)], 因此微小的光谱包络数据的预测误差所导致对被测目标的误差很小。 本实验中游标传感器放大倍数M为~8, 根据式(1)可以计算出, 当预测数据加长后, 在第5个预测包络峰值处, 产生0.02 nm的预测误差, 此时对应单个F-P腔光谱误差也仅为~0.002 5 nm。 实际中如对单个F-P腔传感器采用光谱解调法解调, 欲达到如此小的测量误差也是很困难, 需要光谱的分析精度极高才能实现。 综上说明Bi-LSTM网络预测数据的准确度是较理想的, 本算法是一种非常有效的游标传感器的输出解调方法。

(2)不同浓度被测气体情况下, Bi-LSTM模型预测准确度的测试

将传感器置于氢气浓度分别为1%、 2%、 3%、 4%的环境中, 采用1 450~1 550 nm工作范围的超连续光源获取传感器在不同浓度下的完整光谱数据, 结果如图7所示。 同样, 截取1 450~1 460 nm范围内传感器输出光谱数据, 经过预处理后将其输入至Bi-LSTM网络中进行光谱数据预测, 预测波长范围为1 460~1 550 nm, 实测及预测的光谱数据如图7所示, 并提取预测和实测光谱数据中的峰值波长对比误差, 结果列于表2中。 从图7及表2可以看出, 不同被测气体浓度下, Bi-LSTM网络预测的光谱包络数据依旧和原始实测包络数据具有很好的吻合度, 在各个波峰处预测的波长误差很小(最大误差仅为0.02 nm), 满足实际需求。

图7

Fig.7

	Figure Option ViewDownloadNew Window
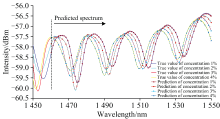	图7 不同被测浓度下, 传感器原始光谱及预测光谱图Fig.7 original and predicted spectra of sensor for samples with different concentrations

表2

Table 2

表2(Table 2)

表2 不同被测浓度下原始光谱及预测光谱结果比较 Table 2 Comparison of raw spectra and predicted spectra of samples with different concentrations 氢气 浓度/% 波峰处真实 波长/nm 波峰处预测 误差/nm 波峰处绝对 误差/nm 1.0 1 465.60 1 465.60 0 1 485.88 1 485.88 0 1 506.16 1 506.16 0 1 526.44 1 526.44 0 1 546.72 1546.74 0.02 2.0 1 463.26 1 463.26 0 1 483.54 1 480.64 0 1 503.82 1 501.72 0 1 524.10 1 522.60 0 1 544.38 1 543.18 0.02 3.0 1 461.82 1 461.82 0 1 482.10 1 482.10 0 1 502.38 1 502.38 0 1 522.66 1 522.66 0 1 542.94 1 542.96 0.02 4.0 1 459.78 1 459.78 0 1 480.06 1 480.06 0 1 500.34 1 500.34 0 1 520.62 1 520.62 0 1 540.90 1 540.92 0.02

表2 不同被测浓度下原始光谱及预测光谱结果比较 Table 2 Comparison of raw spectra and predicted spectra of samples with different concentrations

(3)Bi-LSTM网络泛化能力的测试

进一步验证Bi-LSTM模型对具有不同的包络光谱周期的游标传感器解调的泛化性和有效性, 制备四组具有不同自由光谱范围的F-P腔级联游标效应传感器, 分别为14.78、 24.88、 30.92和35.64 nm。 同样采用超连续光源获取每个传感器原始光谱数据, 截取其中的1 450~1 460 nm范围的光谱数据, 经过数据预处理后, 输入至Bi-LSTM网络中进行数据预测, 预测光谱范围为1 460~1 550 nm。 预测结果经过反归一化、 中心线补偿等处理后, 与实测光谱数据对比, 结果如图8所示, 并从图8提取原始及预测光谱的波峰值, 计算误差, 结果如表3所示。 从图8及表3可以看出, 在各个波峰处, 波长预测误差很小, 最大误差都同样仅为0.02 nm。 说明本文预测模型对不同包络周期的游标传感器光谱数据的预测具有很好的泛化性, 适用于不同包络周期的游标传感器的光谱数据预测。

表3

Table 3

表3(Table 3)

表3 不同包络周期数据FSR预测结果比较 Table 3 Comparison of FSR prediction results with different envelope period data FSR /nm 最小波峰 误差/nm 最大波峰 误差/nm RMSE /nm 14.78 0 -0.02 3.05× 10-3 20.28 0 -0.02 8.69× 10-3 24.88 0 0 9.72× 10-5 30.92 0 0 5.53× 10-5 35.64 0 0 1.50× 10-5

表3 不同包络周期数据FSR预测结果比较 Table 3 Comparison of FSR prediction results with different envelope period data

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同包络周期数据FSR预测图 (a): 14.78 nm FSR 解调信号; (b): 24.88 nm FSR 解调信号; (c): 30.92 nm FSR 解调信号; (d): 35.64 nm FSR 解调信号Fig.8 FSR prediction for data with different envelope periods (a): 14.78 nm FSR demodulation signal; (b): 24.88 nm FSR demodulation signal; (c): 30.92 nm FSR demodulation signal; (d): 35.64 nm FSR demodulation signal