频率分解是一种用于分解复杂信号的数学方法, 它可以有效地分离信号的不同频率成分, 并提取信号的主要特征, 并且对分解后的各个分量进行加权求和可得到原始信号, 其优点是能够自主选择分解个数或者采用非递归方式求解。 设原始信号S分解为k个分量U, 为得到分解序列是有限带宽的中心频率的分量, 且各分量估计带宽之和最小, 所有分量相加等于原始信号为约束条件, 具体约束变分表达式为:

$\min \left(\left\{u_{k}\right\},\left\{u_{k}\right\}\right)\left\{\sum_{k=1}^{k} \partial_{t}\left[\left(\delta(t)+\frac{j}{\pi t}\right)^{*} u_{k}(t)\right] \mathrm{e}^{j u_{k} \ t} \frac{2}{2}\right\}$(1)

$\text { s. t. } \quad \sum_{k=1}^{k} u_{k}=S$(2)

式(1)和式(2)中: ∂t*为Hibert Huang变换得到的单边频谱; δ (t)为狄拉克函数; S为原始信号; * 表示卷积符号; u_k表示全部分量的集合; k代表分解尺度; w_k表示中心频率此时在第k个分量; $\sum_{k=1}^{k} u_{k}$表示全部分量相加之和。

引入惩罚因子α 和拉格朗日乘子λ , 可以使分解摆脱约束限制, 得到新的增广函数式, 由于式(2)的解就是所寻的每个频率分量的中心频率, 为此, 通过交替方向乘子法不停地迭代优化, 即可找到每个频率分量的最优中心频率。

Savitzky-Golay (SG)滤波器^[13]能够对成组的数据进行处理, 以平滑数据, 可以维持信号变化趋势和宽度的同时提高数据的精准度。 其原理是以卷积的形式, 利用线性最小二乘法的原理取一定长度的连续数据与构造好的多项式进行拟合。 设窗口内的一组数据为x[i], i=-m, …, 0, …, m, i为连续的2m+1个整数值, 则可构造出一个n阶多项式(n≤ 2m+1)进行数据拟合

$f(i)=\sum_{k=0}^{n} b_{n 0}+b_{n 1} i+b_{n 2} i^{2}+\cdots+b_{n n} i^{n}$(2)

式(2)中: n为多项式的阶次, b为第i个数据的系数, 并且取值要小于2m+1, 为使拟合结果最好, 其残差平方和应最小, 即上式的系数b_n偏导数应为0。 当已知拟合的多项式阶次n、 单边点数m和待拟合数据x[i]后, 可利用偏导数为0这一性质求解出该窗口内的中心点估计值, 不断重复移动窗口即可求出其他点的中心估计值。

拟合多项式的阶次通常为比较小的阶次即可达到较好的效果, 本工作选定阶次为3阶; 而滤波框长对滤波效果的影响相对较大, 过大则会改变曲线的整体变化趋势, 过小则不能对曲线的平滑起到有效的作用。 在此提出框长调节因子P, 其受相关系数、 信噪比、 均方根误差影响, 且P值越接近0表明框长参数选取越优, 其关系式为

P=RMSEΔSNR×ρXY(3)

将其进一步展开有

$P=\frac{\sqrt{\mathop{\sum }_{i=1}^{n}{{({{Y}_{i}}-{{Y}_{i\_original}} \ \ \ \ \ \ )}^{\ 2}}\div n}}{\left( 10lg\frac{S}{N}-10lg\frac{{{S}_{0}}}{{{N}_{0}}} \right) \ \times \ \frac{Cov\left( Y,~{{Y}_{original}} \ \ \ \ \right)}{\sqrt{D\left( Y \right)} \ \ \ \times \ \sqrt{D\left( {{Y}_{original}} \ \ \ \ \right) \ \ } \ \ \ } \ \ \ }$(4)

式(4)中, S为算法处理后的信号功率, N为算法处理后的残余噪声功率, S₀为原始标准信号功率, N₀为原始标准信号中添加的噪声的功率, Y_i为第i个观测值, Y_{i_original}为第i个预测值, n为观测值的个数, Cov(Y, Y_original)为Y与Y_{i_original}的协方差, D(Y)为Y的方差, D(Y_original)为Y_{i_original}的方差。

本工作采用CO₂的中心波长为1 578.222 nm处的吸收光谱线, 对其二次谐波进行仿真和降噪处理分析。 其中, 在二次谐波理论曲线的基础上引入随机高斯白噪声和伪随机函数模拟的激光强度噪声。 如图1(a)为二次谐波理论信号, 选取最佳调制度为2.2; 图1(b)为含噪二次谐波信号, 信噪比为-8.131 dB。 为方便后续进行算法降噪性能比较, 在此定义二次谐波的相关信息: 峰值、 峰谷值、 峰位、 全宽如图1(a)标注所示。 结合其他领域信号降噪方法研究来看, 基本以变分模态分解和小波变换对于信噪比较差的弱信号在信噪比提升具有较好的优势^{[4, 5]}。 为了进一步验证FD-SG复合降噪算法, 与EEMD-WD方法^[4]以及VMD-WTFD方法^[5]进行综合对比。

图1

Fig.1

	Figure Option ViewDownloadNew Window
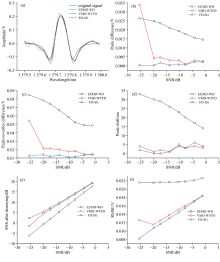
	图1 CO2二次谐波仿真光谱信号 (a): 二次谐波理论谱线; (b): 含噪二次谐波谱线Fig.1 Simulations of the Second harmonic signal of CO2 (a): Theoretical curve; (b): Theoretical curve with noise

以图1(b)含噪二次谐波信号为例, 依据FD-SG复合算法, 选取FD分解频率层数为4, 最优平衡参数为61 000, SG滤波的最优框长设为187, 滤波前后的谐波信号如图2(a)所示。 同样以图1(b)含噪二次谐波信号为例, 采用EEMD-WD方法和VMD-WTFD方法降噪以后的信号曲线如图2(a)所示。 由图2(b)— (f)比较结果可以看出, 本文所提出的FD-SG复合降噪算法对于含噪二次谐波光谱信号的噪声抑制以及相对于理论曲线的有用信号恢复质量都优于其他两种参考算法, 尤其是信噪比较低的情况下FD-SG具有更好的效果。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 二次谐波光谱降噪信号及特征值随信噪比变化关系 (a): 降噪后的二次谐波信号; (b): 峰值差; (c): 峰谷值差; (d): 峰位差; (e): 信噪比改善; (f): 均方根误差Fig.2 Denoised second harmonic signal of CO2 and the relationships between the characteristic points of the curves and SNR (a): Denoised curves; (b): Peak-to-peak differences; (c): Peak-to-valley differences; (d): Center peak wavelength drift; (e): Improved SNR; (f): RMS error

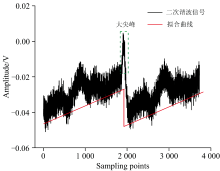
选用中心波长为1 578.222 nm处的吸收光谱线, 对空气中的CO₂进行TDLAS吸收光谱线的二次谐波信号采集实验, 其中TDLAS的锯齿扫描信号幅度为2.4 V、 频率为5 Hz, 正弦波调制信号幅度为0.9 V、 频率为2 kHz, 系统吸收光程为实验室室内开放式的空气路径、 距离约9.5 m。 调节锁相放大器等仪器参数, 检测得到的二次谐波信号如图2所示, 其中红色线条为锯齿波扫描对应的光电检测信号的拟合曲线。 需要说明的是: 本文相关数据中的横坐标是以数据采样点数来表示, 它对应着二次谐波信号的波长(或频率)信息; 为讨论二次谐波波形恢复质量方便记, 本文采用类似于文献[5, 8]的表示方式; 在下文进行频率分解时, 又将横坐标看作是时域坐标来处理, 但其实际光谱物理量依然是波长(或频率)。

由图3可看出针对空气中CO₂微弱气体检测得到的二次谐波信号包含大量噪声, 且在扫描周期的交界处伴有大尖峰噪声结构, 这与文献[5]描述现象相对应。 这是由于TDLAS波长调制解调技术中采用锯齿波信号改变激光器输出波长, 以扫描得到相应的吸收光谱。 根据傅里叶变换可知, 锯齿波扫描周期的交界处也是该信号发生突变的地方, 含有丰富的频率成分。 因此经过锁相放大器进行二次谐波处理后所得到的信号中不可避免地存在大尖峰这样的噪声成分。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 空气中CO2二次谐波信号(两个周期)Fig.3 Second harmonic signal of CO2 in the air (two cycles)

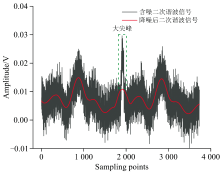
接下来对图3进行拟合曲线扣除处理, 这样可以有效抑制背景噪声, 得到的曲线结果如图4黑色实线所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 扣除拟合曲线以及降噪后的二次谐波信号Fig.4 Subtracted fitted curve and denoised second harmonic signal

拟合曲线相对于吸收线变化部分来说可以看作是慢变化过程。 尤其是大尖峰区域所对应的拟合曲线部分, 可以明显看出和大尖峰结构有很大区别。 仅通过对含噪信号进行拟合曲线扣除处理并不能很好地抑制大尖峰结构, 这是不利于通常的二次谐波信号降噪处理的。

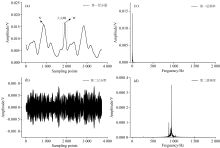
接下来对该信号首先进行频率分解。 为便于FD处理, 将各层分量看作是时域信号, 则其经过傅里叶变换得到的频率分布分别如图5(c)和(d)所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 含噪信号的频率分解及其相应频谱 (a): IMF1; (b): IMF2; (c): IMF1的频率分布; (d): IMF2的频率分布Fig.5 Frequency decomposition of the noisy signal and its corresponding spectrum (a): IMF1; (b): IMF2; (c): Frequency distribution of IMF1; (d): Frequency distribution of IMF2

由图5可看出含噪信号经频率分解后, 有效信号主要集中在第一层分量[图5(a)], 第二层分量主要是噪声成分[图5(b)], 且各层分量间未发生混叠现象。 但对大尖峰噪声结构依然未产生明显的消弱效果, 且在第一层分量内仍残留部分低频噪声。 如前所述, 对于大尖峰这样具有剧烈变化特征的时域信号进行傅里叶变换, 则其低频成分会依然保留在第一层分量中而无法去除, 从而使得FD算法处理后得到的第一层分量中依然有大尖峰特征。

再利用SG滤波进行处理。 为进一步分析二次谐波峰值和大尖峰峰值与滤波框长参数的关系, 定义大尖峰峰值为M、 二次谐波峰值为N, 如图5(a)所示标注。 则二次谐波峰值与大尖峰峰值的比R=N/M, 经不同框偿参数下滤波后, 结果如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 N、 M和R与SG框长参数关系曲线 (a): N、 M与SG框长参数关系; (b): R与框长参数关系Fig.6 Curves of N, M, and R in relation to SG window length parameters (a): Relationship between N, M, and SG window length parameters; (b): Relationship between R and SG window length parameters

二次谐波峰值N和大尖峰峰值M随着SG滤波框长的增大均在不断减小, 且M减小的趋势远大于N, 相对说明了SG滤波可以有效地消弱大尖峰对二次谐波的影响; R随着SG框长参数的增大逐渐增大, 反映了二次谐波峰值和大尖峰峰值随着SG框长参数变化而相对变化的趋势。

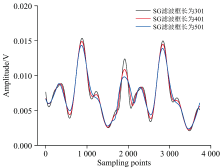
由图7可看出, 随着SG框长的逐渐增大, 降噪后的二次谐波信号波形整体也会发生相应变化。 在尽可能抑制大尖峰的同时, 考虑到二次谐波的整体形态, 本文在实验测量时选择SG滤波框长为401, 对经频率分解后的各层分量分别进行SG滤波处理, 再重构可得二次谐波信号, 结果如图4红色曲线所示。 由图4可以看到, 经过本文复合降噪算法处理后的结果, 大尖峰结构被明显消弱, 且二次谐波信号中的噪声同样得到了很好的抑制, 整体恢复出了较为理想的二次谐波信号。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同SG框长参数下的降噪效果图Fig.7 Denoising effect diagrams under different SG window length parameters

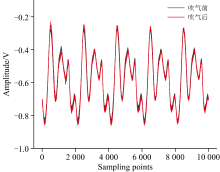
接下来在同等条件下对人体呼出CO₂气体进行二次谐波信号检测。 具体做法是, 实验人员将嘴靠近并沿着激光的传播路径匀速进行吹气, 可以看到二次谐波信号幅值增大的同时还会产生轻微的抖动, 这是由于吹气产生湍流而影响光电探测器上接收到的光信号。 增大的幅值可看做是人体呼出的CO₂的二次谐波幅值, 如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 吹气前、 后的二次谐波信号Fig.8 Second harmonic signal before and after blowing

图8为连续采集5个周期的二次谐波信号, 红色线条表示吹气后的呼出CO₂二次谐波信号, 黑色线条表示吹气前空气中的CO₂二次谐波信号。 为进一步观察人体呼出CO₂的二次谐波信号变化情况, 将吹气后的二次谐波信号减去吹气前的二次谐波信号, 即人体呼出CO₂的二次谐波信号, 如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
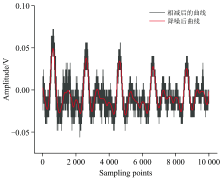	图9 相减曲线降噪前后二次谐波信号Fig.9 Second harmonic signal before and after denoising of subtracted the value before belowing from the value after belowing

通过图9可看出, 随着有效信号幅度的降低, 原本隐藏在二次谐波信号中的噪声成分显现。 利用上述本文提出的FD-SG复合降噪处理过程, 得到降噪后的红色曲线。 可看出本文复合降噪算法可以很好的抑制二次谐波信号中的噪声, 恢复到较为平滑的二次谐波信号, 且对扫描周期交界处的大尖峰同样具有很好的消弱效果。

如图9所示, 经降噪后的五个连续二次谐波信号峰值分别为: 0.049 23、 0.037 99、 0.034 26、 0.027 78和0.025 52 V, 其峰值呈逐渐减小趋势, 这是由于吹气后气体的自由扩散使得检测人体呼出后的CO₂的二次谐波信号峰值开始逐渐趋近于空气中的CO₂的二次谐波信号水平, 从而使得人体呼出CO₂的二次谐波信号减去空气中CO₂的二次谐波信号的结果逐渐趋近于零。