引用本文
田富超, 张海龙, 苏嘉豪, 梁运涛, 王琳, 王泽文. 基于WOA-WNN-LSTM算法的红外CO痕量气体压力补偿与时序浓度分析[J]. 光谱学与光谱分析, 2025,45(4): 994-1007.
TIAN Fu-chao, ZHANG Hai-long, SU Jia-hao, LIANG Yun-tao, WANG Lin, WANG Ze-wen. Pressure Compensation of Industrial Ambient Gases and Their Prediction Based on Infrared Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2025,45(4): 994-1007.
Doi:10.3964/j.issn.1000-0593(2025)04-0994-14  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于WOA-WNN-LSTM算法的红外CO痕量气体压力补偿与时序浓度分析
田富超1,2,3, 张海龙1,2,3, 苏嘉豪1,2,3,*, 梁运涛1,2,3, 王琳1,2,3, 王泽文1,2,3
1.煤炭科学研究总院研究生院, 北京 100013
2.中煤科工集团沈阳研究院有限公司煤矿灾害防控全国重点实验室, 辽宁 沈抚示范区 113122
3.中国矿业大学(北京)应急管理与安全工程学院安全工程与工程系, 北京 100083
*通讯作者 e-mail: 15670880885@163.com

作者简介: 田富超, 1984年生, 煤炭科学研究总院研究员及中煤科工集团沈阳研究院有限公司/煤矿灾害防控全国重点实验室、 分院总工程师 e-mail: tianfuchao@cumt.edu.cn

收稿日期: 2024-06-24 修订日期: 2024-10-18
基金: 国家自然科学基金项目(52174229, 52174230), 辽宁省自然科学基金项目(2022-KF-23-03, 2023-MS-355)资助
摘要

红外光谱分析是工业环境气体定量分析的重要手段, 当前红外气体检测仪的测量精度受环境压力变化影响较大, 导致检测数据在不同压力条件下偏离实际气体浓度。 为提高红外气体传感器的精度, 选择了鲸鱼优化算法(whale optimization algorithm, WOA)和小波神经网络(wavelet neural network, WNN)相结合的压力补偿算法, 并结合长短期记忆法(long short-term memory, LSTM)对补偿后的数据进行预测。 通过搭建工业环境气体压力补偿实验平台, 使用高精度配气仪配置100~900 ppm标准CO气体, 在80~120 kPa范围内进行数百组重复实验, 发现CO气体传感器在负压条件下测量值小于标气浓度, 正压条件下测量值大于标气浓度, 并随压力变化呈线性关系, 绝对误差最高为86 ppm。 将传感器数据使用小波神经网络进行误差降低, 初步补偿后的CO误差降至26 ppm, 但由于参数可移植性较差, 个别数据误差较大。 进一步使用鲸鱼优化算法优化小波神经网络的参数后, 补偿效果显著提升, 传感器测量值与真值之差保持在0.004%以内且数据稳定。 最终结合LSTM进行气体浓度预测, 预测值与实际值之间的均方根误差(RMSE)均小于0.1, 平均绝对误差(MAE)均小于0.020, 实验结果表明, WOA-WNN-LSTM算法能够有效提高红外气体传感器的测量精度, 成功消除环境压力对测量结果的影响, 为工业环境气体检测提供了更为可靠和精准的解决方案。

关键词: 红外光谱分析; 环境压力补偿; 鲸鱼优化算法; 小波神经网络; 时序浓度预测
中图分类号:O657.3 文献标志码:A
Pressure Compensation of Industrial Ambient Gases and Their Prediction Based on Infrared Spectroscopy
TIAN Fu-chao1,2,3, ZHANG Hai-long1,2,3, SU Jia-hao1,2,3,*, LIANG Yun-tao1,2,3, WANG Lin1,2,3, WANG Ze-wen1,2,3
1. Graduate School, China Coal Research Institute, Beijing 100013, China
2. State Key Laboratory of Coal Mine Safety Technology, China Coal Technology and Engineering Group Shenyang Research Institute, Shenfu Demonstration Zone 113122, China
3. Department of Safety Engineering and Engineering, School of Emergency Management and Safety Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China
*Corresponding author
Abstract

Infrared spectroscopy is one of the important means of quantitative analysis of industrial environmental gases. Still, the current infrared gas detector's measurement accuracy is greatly affected by ambient pressure changes, resulting in the detection data deviating from the actual gas concentration under different pressure conditions. To improve the accuracy of the infrared gas sensor, this paper chooses a pressure compensation algorithm combining the Whale Optimization Algorithm (WOA) and Wavelet Neural Network (WNN). It combines it with Long Short-Term Memory (LSTM). Memory (LSTM) to predict the compensated data. By building an experimental platform for gas pressure compensation in industrial environments, using a high-precision gas dispenser to configure 100~900 ppm standard CO gas, and conducting hundreds of repetitive experiments in the range of 80~120 kPa, it is found that the measured value of the CO gas sensor is less than the concentration of the standard gas under negative pressure conditions, and more than the concentration of the standard gas under positive pressure conditions, and the absolute error is linearly correlated with the pressure change, with the highest absolute error of 0.5 ppm. A linear relationship was found, with an absolute error of up to 86 ppm. The sensor data was used to reduce the error using a wavelet neural network, and the initial compensated CO error was reduced to 26 ppm. Still, the individual data error was large due to poor parameter portability. After further optimizing the parameters of the wavelet neural network using the whale optimization algorithm, the compensation effect was significantly improved. The difference between the sensor measurement and the true value was kept within 0.004%, and the data were stable. The root mean square error (RMSE) between the predicted and actual values is less than 0.1, and the mean absolute error (MAE) is less than 0.020. The experimental results show that the WOA-WNN-LSTM algorithm can effectively improve the measurement accuracy of the infrared gas sensors and successfully eliminate the influence of ambient pressure on the results, providing a more reliable and accurate measurement of the gases in industrial environments. It provides a more reliable and accurate solution for gas detection in industrial environments.

Keyword: Infrared spectral analysis; Environmental stress compensation; Whale optimization algorithm; Wavelet neural networks; Time-series concentration prediction
引言

“ 双碳” 背景下, 大气环境污染物的定量检测对气体传感器精度要求逐步提高[1], 在工业环境监测中, 气体检测的准确性对于识别危险源、 预防燃气泄露和可燃气体爆炸、 保护环境以及确保生产安全至关重要。 环境温度和气压变化影响传感器测量痕量气体的准确度, 从而影响工业环境中的安全预警系统[2, 3]。 环境压力的变化会导致单位体积内的气体量变化, 即气体分子间的距离变化, 从而影响红外线吸收能量[4, 5], 即便待测气体浓度未变, 测量值与真实值的偏差也需通过对压力影响的修正校准。

田富超等[5, 6, 7]开发了一种基于非色散红外(NDIR)光谱的新型监测系统, 实现了煤矿井下气体的就地采集、 有源预处理、 原位在线分析, 同时在大气压条件下采用针-环式等离子体发生器对氦气/甲烷-空气进行电离, 研究了放电电压、 电极间隙、 高压电极放电末端与接地电极的距离及氩气体积流量对射流长度的影响, 结果表明: 等离子体射流的最大长度可以达到80 mm; 高压电极放电端与接地端之间的距离越大, 射流长度越长但并非线性增长。 梁运涛等[8, 9, 10]使用傅里叶变换红外(FTIR)光谱仪开发了一套用于监控废气浓度的便携式气体分析仪, 分析物各组分的检出限均小于10× 10-6, 并且提出了一种基于红外气体传感器的温度补偿方法, 采用GA-BP神经网络降低红外气体传感器误差。 相关学者采用了可调谐激光器, 选择不同待测气体的吸收峰, 实现多组分气体的同时测量, 通过多项式修正以及BP神经网络方法对测试数据进行环境参数补偿, 实验证明经过BP神经网络补偿的测试数据总百分比误差为4.707%, 优于多项式修正结果。 钱力等[11]通过对比传感器参比信号与测量信号拟合传感器公式模型, 进行传感器测量值计算, 通过对测量值的计算可以减小温度、 压力等环境因素对二氧化碳传感器测量精度的影响。 赵庆川[12]针对工业燃煤废气中CO2浓度高的特点, 设计了一种具有温度和压力补偿、 基于非色散红外检测技术的全量程CO2传感器。 翟波[13]等研究了光干涉式甲烷传感器有关影响气体折射率的因素, 如温度和压强等化境参数; 设计了适用于光干涉甲烷传感器的补偿算法, 获得良好的实验效果。 赵正杰等[14]采用灰狼智能优化算法-误差反向传播(GWO-BP)神经网络对环境温度与气压变化引起的测量误差进行了补偿, 进行神经网络补偿后的浓度数据在0~2 000 ppm范围内误差为± 15 ppm, 满量程误差为0.75%FS(full-scale), 有效提升了传感器的测量精度与稳定性。 Wang等[15]构建了改进的深度双向递归神经网络(BRNN)模型, 解决化学气体传感器阵列的交叉敏感性问题; 研究中制备了包含四个单元的化学气体传感器阵列, 并全面获取了响应数据。 通过研究数据预处理方法、 模型结构超参数和优化器, 最终开发了一个包含三层和100个隐藏单元的改进深度BRNN模型, 采用Adamax优化器训练, 识别准确率达到98.93%。 相关学者采用随机森林(RF)方法准确测量环境气体浓度, 更好地解决了温湿度漂移, 环境气体传感器阵列的准确性提高约1%, 证明了该策略在准确性和运行时间上均优于传统方法, 如RBF神经网络和BP神经网络。 Buchwitz等[16]采用加权函数修正的差分光学吸收光谱, 研究了一种快速且准确检索大气痕量气体总量的新方法。 Li等[17]提出一种结合改进AdaBoost.RT算法的自适应突变粒子群优化支持向量回归(AMPSO-SVR)算法降低了由于环境温度变化而出现的传感器精度非线性改变, 实验表明该算法在测量降低环境温度引起的误差有明显效果。 Lu等[18]推导出温度变化与温度引起的振荡频率偏移之间的函数关系, 采用这种函数关系和温度传感器降低由环境温度引起的传感器误差。 朱湘飞等[19]探究温度和压强对差分吸收CO2探测激光雷达数据反演的影响得出结论, CO2的吸收截面随压强的增大成指数形式连续减小, 得出吸收截面随温度升高线性增加, 线性系数随压强变化不明显。 温度、 压强对CO2光谱吸收强度的影响较大。 方晶晶等[20]采用小型加压仓, 在CO2分压不变的情况下研究CO2对压力变化的影响规律, 研究发现CO2传感器浓度输出值随压力升高标气值与实测值的比值接近幂函数的形式, 因此得出结论CO2传感器受压力影响可以使用传统经验公式进行补偿。 周洁等[21]测量SO2在变压条件的透射率, 根据郎伯比尔定律计算出SO2的单色吸收截面, 实验结果表明, SO2的单色透射率随着压力增大而逐渐增大, 最大变化率约为40%, 单色吸收截面随压力增大而逐渐减小最大变化率为35%。

尽管国内外学者已经采用了多种方式来减少环境参数对气体传感器精度的影响, 并开创了许多补偿方法, 而在实际应用中, 这些方法的补偿效果仍然有限[22, 23], 尤其是在对气体进行痕量监测时, 其精度往往无法满足实际需求。 本研究提出了一种改进并结合的WOA-WNN-LSTM优化算法, 旨在更精确地降低由于环境温度和压力变化所引起的传感器精度非线性变化。 通过运用该算法, 可以实现对CO痕量气体的精确监测, 有助于推动相关行业的可持续发展与进步。

1 实验部分
1.1 平台搭建

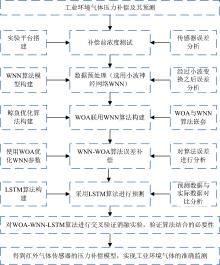
为了验证WOA-WNN-LSTM算法对工业环境痕量气体在线监测补偿效果, 搭建了如图1所示的实验平台, 实验平台由标准气源、 高精度配气仪(TZX-5000A型)、 CO气体传感器、 工控机、 电脑、 TZX-4000A型光谱气体传感器环境压力补偿测试仪、 管线组成。

图1 实验平台Fig.1 Experimental platform

(1)标准气源: 考虑到传感器的量程需求, 选择符合《压缩气瓶灌装规则》(GB/T14194— 2017)气体浓度, 认为所选用的标准气体浓度符合实验要求, 具体气体参数详见表1。

表1 实验气体参数 Table 1 Experimental gas parameter information

(2)高精度配气仪(TZX-5000A型): 采用较高精度的控制背景气体与待测气体进气流量方式控制输入的待测气体, 误差不超过0.19%。

(3)NDIR红外一氧化碳传感器相比同类型传感器有较大优势。 一氧化碳在红外波段吸收较强, 因此优于紫外光谱; 激光传感器的分辨率较低一般为1 ppm不选用激光传感器, 同为红外原理的FTIR传感器造价高, 仪器笨重不适合移动测量也不选用。 实验所选用的传感器为CO气体传感器, 传感器技术参数如表2所示。

表2 传感器技术参数 Table 2 Sensor data sheet

(4)工控机: 监控整个实验系统的运行状态, 便于查看系统的各部分信息如红外气体传感器温度、 检测浓度变化情况、 检测次数等。

(5)环境压力补偿装置: 主要由密封罐和抽吸控制盒两部分组成。 装置主体为密封罐, 密封罐包括罐体和罐盖, 罐体上面安装有保证压力测量装置内部压力的进出气路接口, 还有用于压力测量装置与外部连接的接线连接器, 以及连接抽吸控制盒的气路接口, 罐体周围安装有数字压力表, 方便改变罐内压力时数据的读取与操作。 抽吸控制盒主要由外壳、 气泵、 手动阀和电控四部分组成。 通过手动换向阀的切换实现抽气或吸气, 以方便改变罐内压力。

1.2 实验方法

由于不同场景下一氧化碳浓度差异较大, 在城市空气中, 一氧化碳的浓度通常较低通常不超过10 ppm, 在火灾现场, 一氧化碳浓度可以非常高。 由于燃烧过程中的不完全燃烧, 一氧化碳浓度可能达到几百到几千 ppm, 露天矿区, 尤其是在爆破或车辆大量使用的区域, 一氧化碳浓度可以显著提高。 根据矿区的具体操作条件, 浓度可能从几百到几千 ppm不等, 因此实验将选用量程为0~1 000 ppm的CO传感器可囊括CO传感器大部分使用场景。 对于气体配置, 需要在气体管路串联连接并将其接入高精度配气仪(TZX-5000A型)中, 将待测气体气瓶与背景气体气瓶接入管路, 同时调整进气流量为300 mL· min-1, 气体流动的过程中会带走一部分热量故气体流量对压力补偿装置中的温度环境会造成一定影响从而带来实验误差。 首先将选定浓度范围的待测气体与99.999%浓度N2通过高精度配气仪制成不同浓度下的待测气体, 打开气体管路控制开关使待测气体进入压力补偿装置中, 通过传感器进行浓度测量后, 由传感器所连接PU管进行排空处理。 因RS-422定义了一种平衡通信接口, 将传输速率提高到10 Mb· s-1, 由于RS-422接口串行线的单端通信特性, 数据传输线并联布置, 三个传感器的信号输出连接到数据终端设备(DTE, 如PC)。 通过这种方式, 可以实时传输数据, 包括测量信号、 参考信号、 吸光度、 测试气体浓度、 传感器温度和测量次数。 在上述基础上, 可以完成相应传感器的标定和测试, 为进一步分析气体传感器的精度和稳定性提供数据。

(1)选用0~1 000 ppm的CO的红外光谱传感器, 依次进行实验, 首先打开电源进行高精度配气仪和传感器的预热(约30 min), 待压力补偿装置上的压力表显示压力稳定后开始进行下一步实验。

(2)打开N2气瓶阀门, 设置高精度配气仪通入气体为N2, 使得N2进入到压力补偿密封罐体中, 从而排出罐内杂气。

(3)设置标定浓度, 一般选用传感器量程的50%作为标定浓度, 打开N2气瓶和待测气瓶(CO)阀门, 同时在高精度配气仪设定通入气体种类和流量(500 mL· min-1)以及混合气体的浓度。

(4)通过抽吸控制盒通入或者吸出气体来改变压力补偿密封罐内的压力, 使得密封罐内压力依次为80、 85、 90、 95、 100、 105、 110、 115和120 kPa, 背景气体N2和待测气体持续不断经高精度配气仪保持通入状态, 在每一压力条件下, 通过工控机控制使传感器温度稳定在室温, 待电脑显示屏显示待测气体浓度稳定后即可进行下一组浓度的气体测试。

(5)实验完成后使用背景气体对传感器进行3 min的冲洗, 以排除内部残留的气体杂质确保传感器的稳定性与准确性。

(6)导出实验所测得的在不同压力下待测气体(CO)各标准浓度的实测浓度数据, 并求取平均值。

(7)分别使用WNN预理数据以及WOA优化后的WNN算法对当前数据进行补偿, 对比并且使用LSTM算法预测气体浓度。

(8)通过消融实验, 验证WOA、 WNN和LSTM三个模块对模型性能的独立贡献。 去除WOA, 仅使用WNN对数据进行初步补偿, 再使用LSTM进行时序预测, 记录预测的气体浓度和模型误差; 去除WNN, 仅使用WOA优化LSTM进行气体浓度预测, 分析模型的补偿效果, 并记录模型误差; 去除LSTM, 仅使用WOA优化后的WNN对气体浓度进行补偿, 不进行时序预测, 记录并分析模型误差。 将各实验结果与完整的WOA-WNN-LSTM算法结果进行对比, 分析各模块对补偿效果的影响。

(9)对补偿前后的数据作图对比分析误差补偿效果, 对预测数据以及实际数据作图进行对比, 由RMSE得出优化算法的预测性能, 在优化算法性能良好的情况下将其进行现场工程应用。

整体技术路线如图2所示。

图2 技术路线Fig.2 Technology roadmap

2 数据分析
2.1 补偿前数据分析

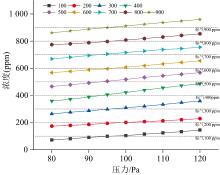
为准确评估CO气体在不同环境压力下的行为, 进行一系列详尽的实验, 测定CO气体在不同压力条件下的多点浓度。 如图3及图4所示, 随着环境压力的增加, CO气体实测浓度也在逐渐增大。 在负压条件下, CO气体实测浓度一般低于标准气体浓度, 在接近大气环境压力条件下, CO气体实测浓度与标准气体浓度也最为接近; 在正压条件下, CO气体实测浓度则基本高于标准气体浓度。 CO气体浓度随压力变化近似呈线性关系。 随着环境压力偏离标准压力CO气体浓度误差值逐渐增大, 浓度误差最大为86 ppm。

图3 传感器浓度平均值Fig.3 Average sensor concentration

图4 传感器误差浓度平均值Fig.4 Average sensor error concentration

2.2 补偿后的数据分析

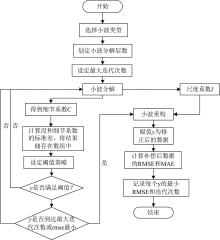
小波神经网络(wavelet neural network, WNN)具有强大的函数学习能力, 可以学习并适应各种复杂的非线性函数, 具有较强的自适应性[24], 如图5所示小波神经网络可以处理非平稳信号降低误差, 因此适合应用于光谱气体传感器的信号处理[25], 由于小波神经网络参数调整难度大, 小波神经网络效果受阈值等参数影响较大, 因此选用结构简单参数少且搜索能力强的鲸鱼优化算法计算小波神经网络的阈值等参数, 提升小波神经网络降低误差的能力。 最后使用长短期记忆法来预测未来一个时段的气体浓度。

图5 WNN算法流程图Fig.5 Flow chart of the WNN algorithm

2.2.1 WNN数据分析

小波神经网络(wavelet neural network, WNN)是一种基于小波变换理论构造而成的神经网络, 其将原先隐含层的Sigmiod激活函数替换为小波基函数, 如Morlet小波函数, 这一特性充分利用小波变换的局部化性质以及神经网络的大规模数据处理、 学习能力, 具有较强的收敛能力和较快的收敛速度, 如图5所示。

为精确补偿传感器在环境压力波动下的测量误差, 小波神经网络的训练过程旨在通过以下关键步骤来优化网络性能:

①初始化网络参数, 包括输入节点个数、 输出节点个数、 隐含节点个数、 学习率、 迭代次数、 权值矩阵、 小波尺度因子和平移因子等; 在对小波神经网络(WNN)进行超参数优化时, 使用交叉验证方法, 以不同的隐含层节点数和学习率组合为参数进行实验。 如图6(a— d)所示, 隐含层节点数和学习率的组合对模型性能有显著影响。 隐含层节点较少时(如5或10个), 模型的拟合能力较弱, 尤其在较低的学习率(如0.001)下, 无法充分学习数据特征, 导致均方误差(MSE)较高。 当隐含层节点数增加到15时, 模型的拟合能力明显提升, 尤其是在学习率0.1的情况下, MSE显著降低, 达到了最佳效果。

图6 交叉验证对比图Fig.6 Cross-validation comparison chart

实验结果显示, 选择隐含层节点数为15、 学习率为0.1的配置可以获得最优性能。 模型的均方误差大幅下降, 说明网络能够在较复杂的结构下更好地捕捉数据中的关键特征, 并具有较快的收敛速度。 相比于其他组合, 这一参数配置能够在保证模型精度的同时, 加快训练过程, 提高模型的泛化能力。

选择上述参数配置的原因为, 通过多次平行实验和交叉验证, 发现隐含层节点数较少会导致模型欠拟合, 而学习率过低则使得模型收敛速度过慢。 通过实验优化后, 选择15个隐含层节点和0.1的学习率, 能够在较复杂的网络结构下快速收敛, 显著降低均方误差, 确保模型的稳定性与预测精度, 参数选择如表3所示。

表3 WNN主要参数表 Table 3 Main parameters of WNN

②对输入输出数据进行标准化处理, 确保数据在适当范围内, 以避免量纲和尺度对网络性能的影响;

z=x-μσ(1)

式(1)中, z为标准化后的值; x为原始数据值; μ 为原始数据均值; σ 为原始数据的标准差。

μ=1N∑i=1Nxi(2)

式(2)中, N为数据点个数; xi为数据集中的每个数据点。

σ=1N∑i=1N(xi-μ)2(3)

式(3)中, N为数据点个数; xi为数据集中的每个数据点; μ 为原始数据均值, 如表3所示。

③采用误差反向传播算法, 进行网络的前向计算和误差反向传播, 根据误差梯度调整权值、 尺度因子和平移因子, 使网络输出逐渐逼近期望输出, 直到满足终止条件, 如误差小于设定阈值或达到迭代次数上限。

④进行网络的测试和验证, 使用训练好的网络对新输入数据进行预测, 评估网络的泛化能力和预测精度。 若结果不满意, 可调整网络参数或增加训练数据量, 并重新进行训练。 在环境压力波动下传感器精度测量精度补偿方向, 可使用小波神经网络来进行预补偿。 首先收集训练数据集, 包括传感器在不同压力下的输出信号和相应的实际浓度数据。 然后构建小波神经网络, 将传感器输出作为输入, 实际浓度作为期望输出, 并选择合适的网络参数。 再利用误差反向传播算法训练网络, 根据误差梯度调整参数, 使网络输出逼近实际浓度值。 最后测试和验证网络, 使用训练完成的网络对新的传感器输出信号进行预测, 评估网络的补偿效果和预测精度, 并根据需要调整网络参数或增加训练数据。

2.2.2 WOA-WNN联用数据分析

由于小波神经网络参数调整难度大同时训练效果受参数影响较大, 因此使用嵌入鲸鱼优化算法的小波神经网络计算小波神经网络最优权值矩阵。 鲸鱼优化算法主要包括三个步骤, 即包围捕食, 气泡攻击以及寻觅食物阶段[26]。

距离食物最近的鲸鱼作为局部最优解, 剩余鲸鱼朝这个位置靠近, 逐步包围食物, 使用下列的数学模型表示

D→=|C→·X→(t)-X→(t)|(4)

X→(t+1)=X→(t)-A→D→(5)

式(4)和式(5)中, D→为搜索代理到目标实物的距离向量, t为当前的迭代次数。 C→和A→是系数向量, X→(t)为当前的局部最优解, C→和A→的表达式如式(6)和式(7)

C→=2r→(6)

A→=2a→r→-a→(7)

式(6)和式(7)中, a→表示从2到0的线性递减向量, r为0到1之间的随机数。

鲸鱼在捕食过程中使用气泡进行攻击, 通过收缩包围和螺旋更新位置的方式模拟鲸鱼捕食吐出气泡的行为, 从而逼近食物即目标函数。 当座头鲸发现食物后, 若概率小于0.5, 依然采用传统的方式进行更新, 否则会计算个体与当前最优鲸鱼的距离, 然后再以螺旋方式游走, 在进行食物搜索时, 螺旋游走方式的数学模型如式(8)[27]

X→(t+1)=D→'elbcos(2πl)+X→(t)(8)

式(8)中, D→'=|X→(t)-X→(t)|表示目前鲸鱼种群中最优的个体与当前个体的距离向量, b为常量表示螺旋形状参数, l为值域为[-1, 1]均匀分布的随机数。 X→(t+1)=X→(t)-A→D→为包围猎物的公式。

X→(t+1)=X→(t)-A→D→p< 0.5D→'eblcos(2πl)+X→(t)p≥0.5(9)

式(9)中, p为0~1之间的随机数, 代表鲸鱼个体包围猎物或者螺旋攻击的概率。

为了更好地保证搜索和收敛, 鲸鱼个体可以进行随机搜索食物, 当|A|> 1时, 随机选择的座头鲸个体会引导其他座头鲸向其靠拢。 反之, 当前座头鲸的位置仅仅是一个局部最优的位置, 这种方式保证了座头鲸个体能够进行全局搜索, 获得全局最优解。

D→″=|CX→rand(t)-X→(t)|(10)

X→(t+1)=X→rand(t)-A→D→(11)

式(10)和式(11)中, D→″表示当前搜索个体与随机个体之间的距离, X→rand(t)表示当前随机个体的位置。

WOA算法首先随机初始化一组, 在每次迭代中, 搜索代理根据随机选择的搜索代理或到目前为止获得的最优解更新它们的位置。 将a参数由2随迭代次数降为0, 从而由探索逐步到利用。 当|A|> 1时选择随机搜索代理, |A|< 1时选择最优解更新搜索代理位置。 根据p的值, WOA可以在螺旋运动和圆环运动之间进行切换。 最后通过满足终止准则以终止WOA算法, WOA-WNN算法参数如表4所示。

表4 WOA-WNN主要参数 Table 4 Main parameters of WOA-WNN

如图7所示, WOA-WNN优化算法优化过程为初始化WOA参数并且更新迭代WOA参数, 若参数不满足输出条件, 使用鲸鱼捕食的方式进行自适应惯性权重随机游走和带权重的螺旋式位置更新来更新参数, 最终输出最符合数值形式的小波神经网络阈值策略。 在鲸鱼优化算法计算出最适合的阈值策略基础之上进行小波神经网络更新迭代。

图7 WOA-WNN嵌套示意图Fig.7 Schematic diagram of WOA-WNN nesting

将WOA-WNN算法以程序嵌入传感器并进行传感器测试实验, 实验证明, 采用WOA优化WNN参数得到的WNN最优权值和阈值后的算法可提高CO红外光谱传感器受环境压力影响下的精度。

如图8(a— d)所示, 经过WOA优化后的WNN相比未经有优化的WNN精度有较大的提升, 其误差范围也有较大的缩小, 经小波神经网络补偿后的数据, CO降至26 ppm以内、 经过鲸鱼优化算法寻优小波神经神经网络最佳阈值策略, 气体传感器误差降至0.04 ppm以内。 表明优化后的传感器精度有较大提升, 进一步在图8可以看出单独使用小波神经网络进行误差补偿, 其误差不稳定, 在每个浓度条件下都有至少有一种工况条件下压力误差波动范围较大, 尤以300 ppm的测试数据最不稳定, 反观使用鲸鱼优化小波神经网络的标准差十分稳定, 始终保持在0.025以内。

图8 CO不同浓度下WNN与WOA-WNN补偿精度对比图Fig.8 Comparison of the compensation accuracy of WNN and WOA-WNN at different concentrations of CO

在压力为105 kPa与浓度为900 ppm条件下单独使用小波神经网络与使用鲸鱼优化小波神经网络得出的平均值与标准差十分接近, 其主要原因为测试时采用的小波神经网络与鲸鱼优化算法计算出的小波函数类型与小波层数基本一致, 可以获得较好效果, 而是在其他工况条件下测试选用的小波函数与小波神经网络层数以及学习速率都不尽相同, 因此鲸鱼优化算法优化后的小波神经网络在大部分条件下均大幅优于单独使用小波神经网络。

2.2.3 WOA-WNN-LSTM联用数据分析

长短期记忆网络(long short-term memory, LSTM)改良自循环神经网络(recurrent neural network, RNN), 在解决序列数据处理中的长期依赖性问题方面取得了很好的效果。 LSTM网络通过引入门控制机制, 能够有效学习并记忆长序列信息。 LSTM组成部分:

记忆单元(Memory Cell): 负责存储和更新信息。

每个神经网络包括输入门、 遗忘门以及输入门具体作用及计算公式如下所示。

输入门(Input Gate): 决定加入新信息的数量, 以及如何加入, 式(12)为输入门计算公式

it=σ(Wi[ht-1, xt]+bi)(12)

遗忘门(Forget Gate): 控制哪些信息应该被遗忘, 式(13)为遗忘门计算

ft=σ(Wf|ht-1, xt|+bf)(13)

输出门(Output Gate): 决定将哪些信息传递到下一层[28], 式(14)、 式(15)和表1表示输出门的计算

ot=σ(Wo[ht-1, xt]+bo)(14)

ht=ottanh(Ct)(15)

在每个时间步, LSTM网络会根据上一个时间步的输出、 上一个时间步的记忆状态以及当前时间步的输入来计算新的信息, 据式(16)进行更新记忆状态并输出结果[28]。

C~t=tanh(WC[ht-1, xt]+bC)(16)

式(16)中, Wf为权重矩阵, b为偏置系数, xt为当前时刻输入信息。 ht-1为上一时刻的隐藏状态, ht为传递到下一时刻的隐藏状态, σ 为sigmoid函数, Ct为当前的单元状态, Ct-1为上一步骤的单元状态, C~为备选的细胞状态。 ot为输出门。

如图9所示, 数据通过上一时序的神经元, Ct-1和ht-1为上一时序输入对当前神经元的输入, xt为当前神经元的输入。 xt与ht-1作为输入经过sigmoid函数计算出ft经过遗忘门与Ct-1结合决定需要遗忘的数据, xt与ht-1经过sigmoid函数计算出it, 经过tanh函数计算出Ct, it与Ct同时经过输入门, xt与ht-1经过sigmoid函数计算出ot与Ct共同输入记忆单元得出当前的时序数据ht, 将当前的ht和Ct输入到下一神经元完成一次循环[29]。

图9 LSTM算法过程时序图Fig.9 Sequence diagram of the LSTM algorithm

根据上述实验及数据分析, 提出WOA-WNN-LSTM算法是一种基于小波神经网络(wavelet neural network, WNN)、 鲸鱼优化算法(whale optimization algorithm, WOA)和长短期记忆网络(long short-term memory, LSTM)的时序数据预测方法, 可以用以解决气体传感器在压力波动时导致的测量精度降低问题(见表5)。

表5 WOA-WNN-LSTM主要参数 Table 5 List of main parameters of WOA-WNN-LSTM

小波神经网络(WNN)被用于对原始时序数据进行分解, 提取不同频率的特征信号。 WNN的作用为将复杂的时序信号分解成多个尺度的子信号, 可以显著降低数据的噪声和冗余信息, 提高数据的质量。 鲸鱼优化算法(WOA)用于优化WNN的参数。 这一步骤旨在通过调整WNN的参数, 使其输出更接近目标信号, 从而提高WNN的逼近能力和稳定性。 LSTM算法的性能受数据预处理影响较大, 因此通过WOA-WNN算法预处理后的数据输入LSTM算法就会得到更佳的训练效果, LSTM算法的参数设置通过平行实验得到。 图10(a— d)为不同浓度下传感器数据点的分布情况, 经过WOA优化后的WNN输出更为平滑, 数据点分布更加均匀, 说明参数优化过程有效提高了模型的稳定性和逼近能力。 在每个尺度的子信号上, 长短期记忆网络(LSTM)用于捕捉时序数据的长期依赖和动态变化。 LSTM的门控机制和记忆单元使得模型能够更好地处理长时间序列数据, 预测结果更为准确。 图10(a— d)中的不同颜色的点分别代表不同浓度下的预测结果, 可以看出预测误差在所有浓度下均不超过0.04 ppm, 预测数据与真实数据非常接近, 说明算法在捕捉数据的动态变化方面表现出色。

图10 最小二乘法拟合分析图Fig.10 Plot of least squares fitting analysis

整体分析结果, WOA-WNN-LSTM算法有效处理了气体传感器数据的非平稳性和非线性, 通过多层次分解、 优化和组合, 提高了预测的准确性和鲁棒性。 算法结合了WNN的降噪能力、 WOA的全局搜索优化能力以及LSTM的时序依赖捕捉能力, 使其在处理复杂时序数据中表现。

图10(a— d)分别所示, 在不同浓度和压力下, 最小二乘法建立的二元多次函数模型能够较好地拟合气体浓度与压力之间的关系。 图中为浓度随压力变化呈现出线性趋势, 说明最小二乘法可以通过拟合函数较为准确地描述这些变量的基本关系。 拟合曲线的误差较为明显, 尤其是在高浓度和高压力条件下, 模型的拟合误差有所增加, 无法很好地捕捉压力波动引起的浓度变化。 表明虽然最小二乘法适合处理简单的线性或多次方函数关系, 而面对复杂的非线性数据和时序变化时, 其表现存在局限性。

由图11(a— d)所示, 通过消融实验验证了WOA、 WNN和LSTM三个模块对模型性能的独立贡献。 由实验结果可以看出, 单独使用WNN模型时, 模型在不同压力条件下的误差较大, 且在高压条件下波动明显; 引入WOA后, WNN模型的误差显著减少, 尤其是在高压条件下表现出较好的稳定性, 证明了WOA在优化WNN参数方面的有效性。 而加入LSTM进行时序预测后, 模型在动态压力变化下的表现进一步改善, 而单独使用WOA-LSTM的模型在低压和高压下的误差依然较大。 完整的WOA-WNN-LSTM模型在不同压力条件下均表现出最小的误差波动和较高的精度, 证明了该组合在全局优化、 非线性补偿和时序预测方面的协同作用。

图11 消融实验分析图Fig.11 Ablation experiment analysis diagram

图12(a, b)清晰显示不同浓度下的预测结果与真实数据的高度吻合并与最小二乘法同浓度的拟合浓度进行了对比。 通过对比可以看出, 在不同浓度和压力条件下, WOA-WNN-LSTM算法能够更稳定地预测气体浓度, 误差远小于最小二乘法拟合的结果。 分析认为WOA优化了神经网络的参数, 使WNN能够更好地处理非线性信号, 同时LSTM有效捕捉了时序数据中的动态特征, 证明了算法的有效性。 从预测误差不超过0.04 ppm的结果, 算法在高精度预测方面具有较好的算法表现力。

图12 预测值与实际值对比分析Fig.12 Comparative analysis of forecast and actual values

通过与其他模型的对比, 可以看出WOA-WNN-LSTM模型显著优于单独的WNN或LSTM模型, 在各个压力条件下表现出更好的稳定性和精度。 实验结果表明: WOA、 WNN和LSTM模块在提升模型的全局优化能力、 非线性数据处理能力和时序预测精度方面具有独立且重要的贡献。 相比之下, 简单的二元多次函数模型无法有效处理复杂的非线性和动态变化数据, 因此采用WOA-WNN-LSTM算法必要且合理, 有效提升了气体浓度补偿与预测的准确性。

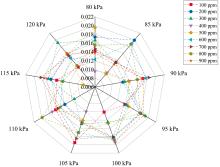
图13为WOA-WNN-LSTM 算法在预测CO的平均绝对误差, 该雷达图表示在不同压力条件下不同CO浓度的平均绝对误差值, 图中的MAE值全部保持在0.020以内说明该算法的误差值较小, 且在合理范围。

图13 MAE分析Fig.13 MAE analysis

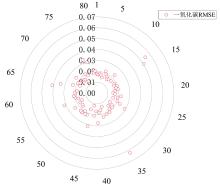
图14为WOA-WNN-LSTM算法在预测CO浓度时的均方根误差(RMSE)分布。 雷达图雷达编号为上文实验流程所述实验工况1— 81号, 圆心到圆周的距离表示RMSE的大小, 越接近圆心误差越小, 越远离圆心误差越大。 图14的RMSE范围从0.00到0.07 ppm, 表明预测误差非常小, 整体预测精度较高。 大多数数据点集中在RMSE较低的区域(0.00~0.03), 说明算法在大部分样本上的预测误差均很小, 预测效果较为理想。 少数数据点的RMSE稍高(0.04~0.07), 但仍处于较低水平, 表明极少数样本的预测误差稍大, 但整体误差控制在合理范围。

图14 均方根误差分析Fig.14 RMSE Analysis

图14中误差最小的部分几乎接近于0, 表明某些样本的预测值与实际值非常接近, 体现算法在特定情况下的卓越性能。 即使在误差较大的情况下, RMSE也没有超过0.07 ppm, 表明算法在处理不同样本时的误差均被有效控制在较小范围内。 这一特点表明WOA-WNN-LSTM算法在不同情况下的鲁棒性和稳定性。 整体数据分布中, WOA优化的效果显著, 使得WNN和LSTM的组合在处理时序数据时具有更好的稳定性和准确性。

3 工程应用

将应用于CO传感器的WOA-WNN-LSTM算法嵌入拓展至CO2、 CH4、 NH3、 SO2、 NO2、 H2S等红外和紫外差分光谱气体传感器, 实现了常量和痕量气体的环境大气压力补偿, 集成研发了可应用于环保、 消防、 职业健康、 露天矿区等领域的如图15所示, TZX-1000A/B/C/D系列的大气工业环境气体在线分析系统, 在中石催化剂大连有限公司工业园区低一氧化碳场景测试结果见表6。

图15 TZX-1000A气体分析仪Fig.15 TZX-1000A gas analyze

表6 光谱气体传感器实测值 Table 6 Measured values for spectral gas sensors

为了进一步验证设备的准确性, 由现场取出一瓶多组分的标气进行验证(氧气18.6%, 甲烷1%, 一氧化碳100 ppm, 二氧化碳3%, 二氧化硫40 ppm, 二氧化氮30 ppm, 氨气20 ppm, 硫化氢100 ppm), 数据结果如表7所示。

表7 标气测试结果 Table 7 Standard gas test results

表6中O2最大误差为0.47, CH4最大误差为0.03, CO最大误差为2.2 ppm, CO2最大误差为0.16以内, SO2最大误差为0.9 ppm, NO2最大误差为1.09 ppm, NH3最大误差为0.6 ppm, H2S最大误差为2.1 ppm。 如表7所示, 表明该算法应用于工业气体分析仪后误差在可接受范围内, 可实现精确监测危险气体。 在实验室中, 实验条件较为理想和可控, 温度、 湿度、 气压等环境参数稳定, 因此传感器的测量误差较小。 而在工业现场, 传感器运行时可能会受到更多的环境干扰, 例如振动、 湿度变化、 温度波动、 气体混合物的复杂性等。 这些因素会影响传感器的准确性, 并且传感器的稳定性可能会因现场环境的随机波动而减弱。 实验室中传感器通常是在单一气体环境下进行测试, 而在工业应用中, 气体传感器可能需要面对多组分气体的复杂环境, 尤其是不同气体之间的交叉干扰效应可能会加剧误差的产生。 这些复杂的现场条件都会导致误差较实验室测试时增大。 传感器误差的增大主要源于现场条件的复杂性和不可控性, 尤其是温度、 湿度、 气体浓度波动等因素都会影响传感器的实际表现。

图16所示为该气体补偿算法可以拓展应用于矿山采掘、 冶金工程、 大气监测等领域。

图16 工业环境多种气体分析系统应用场景Fig.16 Application scenarios of multi-gas analysis system for industrial environment

4 结论

建立环境气压补偿实验平台, 开展80~120 kPa下100~900 ppm的CO气体传感器压力补偿实验, 提出WOA-WNN-LSTM压力补偿算法, 以实现不同压力条件下CO浓度的精确监测。 将本研究中CO传感器补偿算法应用于工业气体分析仪中并拓展到O2、 CH4、 CO2等8种气体传感器中, 在中石化大连催化剂有限公司进行现场实测。

根据实验数据结论如下:

(1)通过环境气压补偿实验平台进行CO浓度变压测试, CO气体浓度随压力变化近似呈线性关系, 且随着环境压力偏离标准压力, CO气体浓度误差值逐渐增大, 浓度误差最大为86 ppm。

(2)将小波神经网络嵌入CO气体传感器, CO气体传感器最大误差由86 ppm降至26 ppm以内, 使用鲸鱼优化算法进一步优化小波神经网络得到传感器测量值与真值之差保持在0.04 ppm内。

(3)进一步使用LSTM算法进行CO浓度预测, 得到气体测试值与真值之间的RMSE保持在0.07 ppm以内, 表明算法整体预测精度较高, 在避免有害气体浓度超限方面提供了一种精确的预测方法。

参考文献
[1] LIU Wen-qing(刘文清). Acta Optica Sinica(光学学报), 2022, 42(6): 0600001. [本文引用:1]
[2] LIANG Yun-tao, TIAN Fu-chao, FENG Wen-bin, et al(梁运涛, 田富超, 冯文彬, 等). Journal of Chinca Coal Society(煤炭学报), 2021, 46(6): 1701. [本文引用:1]
[3] DENG Jun, ZHANG Qi, CHEN Wei-le, et al(邓军, 张琦, 陈炜乐, 等). Safety in Coal Minee(煤矿安全), 2024, 55(3): 99. [本文引用:1]
[4] LIANG Yun-tao, CHEN Cheng-feng, TIAN Fu-chao, et al(梁运涛, 陈成锋, 田富超, 等). Coal Science and Technology(煤炭科学技术), 2021, 49(4): 40. [本文引用:1]
[5] WANG Jin-cheng, LIANG Yun-tao, TIAN Fu-chao(王金成, 梁运涛, 田富超). Safety in Coal Mines(煤矿安全), 2022, 53(11): 98. [本文引用:2]
[6] TIAN Fu-chao, LIANG Yun-tao, ZHU Hong-qing, et al(田富超, 梁运涛, 朱红青, 等). Journal of Central South University(中南大学学报), 2022, 29(6): 1840. [本文引用:1]
[7] TIAN Fu-chao, CHEN Lei, PEI Huan, et al(田富超, 陈雷, 裴欢, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(9): 2694. [本文引用:1]
[8] ZHAO Zhen-zhen, LIANG Yun-tao, JIN Lei, et al(赵珍珍, 梁运涛, 金磊, 等). Safety in Coal Mines(煤矿安全), 2022, 53(8): 74. [本文引用:1]
[9] Liang Yuntao, Tang Xiaojun, Zhang Xuliang. Journal of Spectroscopy, 2015, 15: 2314. [本文引用:1]
[10] Liang Yuntao, Wang Jincheng, Tian Fuchao. Fuel, 2023, 354: 129330. [本文引用:1]
[11] QIAN Li, LIU Li-tao, HUANG Gang, et al(钱力, 刘力涛, 黄刚, 等). Transducer and Microsystem Technologies(传感器与微系统), 2022, 41(11): 57. [本文引用:1]
[12] ZHAO Qing-chuan( 赵庆川). Process Automation Instrumentation(自动化仪表), 2016, 37(12): 79. [本文引用:1]
[13] ZHAI Bo, DAI Jun, WANG Xiao-hong(翟波, 戴峻, 王晓虹). Safety in Coal Mines(煤矿安全), 2017, 48(4): 115. [本文引用:1]
[14] ZHAO Zheng-jie, ZHAO Yong-yi, KONG Chun-xia, et al(赵正杰, 赵勇毅, 孔春霞, 等). Laser and Infrared(激光与红外), 2020, 50(1): 80. [本文引用:1]
[15] Wang Zhen, Li Yanhao, He Xiangnan. Sensors and Actuators B: Chemical, 2024, 401: 134996. [本文引用:1]
[16] Buchwitz M, Rozanov V, Burrowa J P. Journal of Geophysical Research: Atmospheres, 2000, 105(D12): 15231. [本文引用:1]
[17] Li Ji, Zhang Chentao, Zhang Xukun. IEEE Access, 2020, 8: 12413. [本文引用:1]
[18] Lu Wenke, Feng Yang, Zhu Changchun. Ultrasonics, 2017, 76: 87. [本文引用:1]
[19] ZHU Xiang-fei, LIN Zhao-xiang, LIU Lin-mei, et al(朱湘飞, 林兆祥, 刘林美, 等). Acta Physica Sinica(物理学报), 2014, 63(17): 161. [本文引用:1]
[20] FANG Jing-jing, REN Xiao-meng, XU Xin-hong, et al(方晶晶, 任小孟, 徐新宏, 等). Equipment Environmental Engineering(装备环境工程), 2022, 19(7): 129. [本文引用:1]
[21] ZHOU Jie, CHEN Xiao-hu(周洁, 陈晓虎). Journal of Zhejiang University(浙江大学学报), 2006, (6): 947. [本文引用:1]
[22] ZHANG Zhi-rong, XIA Hua, SUN Peng-shuai, et al(张志荣, 夏滑, 孙鹏帅, 等). Acta Optica Sinica(光子学报), 2023, 52(3): 119. [本文引用:1]
[23] ZHANG Zhi-rong, PANG Tao, SUN Peng-shuai, et al(张志荣, 庞涛, 孙鹏帅, 等). Chinese Journal of Lasers(中国激光), 2019, 46(12): 265. [本文引用:1]
[24] LI Shu-xun, WANG Zhi-hui, KANG Yun-xing, et al(李树勋, 王志辉, 康云星, 等). Journal of Vibration and Shock(振动与冲击), 2021, 40(12): 143. [本文引用:1]
[25] DONG Yi, YANG Chuang(董毅, 杨创). Safety in Coal Mines(煤矿安全), 2024, 55(1): 185. [本文引用:1]
[26] Li Maodong, Xu Guanghui, Fu Yuanwang. Journal of Intelligent & Fuzzy Systems, 2022, 42(3): 1501. [本文引用:1]
[27] Mirjalili S, Lewis A. Advances in Engineering Software, 2016, 95: 51. [本文引用:1]
[28] CHEN Lü, LI Hui, LIU Chang(陈律, 李辉, 刘畅). Railway Stand ard Design(铁道标准设计), 2024, 68(4): 203. [本文引用:2]
[29] Ming Hao, Chen Xinyu, Fang Xiansong. Journal of Lightwave Technology, 2022, 40(8): 2427. [本文引用:1]