作者简介: 梁业恒, 1987年生, 中山大学地理科学与规划学院助理研究员 e-mail: liangyeheng@163.com
利用卫星遥感技术对水中重金属浓度进行监测具有重要研究意义。 但由于自然水体重金属含量低, 其遥感反演可行性仍被学界怀疑, 以致该领域发展比较缓慢。 鉴于此, 以中国环境卫星(HJ-1A)高光谱成像仪(HSI)反演水中硫酸铁浓度为例, 采用遥感敏感性分析模型(DDE模型), 模拟得到硫酸铁在理论清深水体和三种常见自然水体: 富营养化水体、 浑浊水体与重金属尾矿污染水体, 共计四种水体类型背景下的可遥感反演下限浓度光谱曲线, 明确地给出不同情形遥感反演下限浓度最小值及其所在波长, 进而分析不同水体类型的遥感敏感性变异规律。 研究结果发现, 在不同水体类型背景下, 硫酸铁的遥感反演下限浓度最小值及所在波长位置均是变化的。 在理论清深水体背景下, 该值的最小值为4.63×10-4 mg·L-1, 出现在468.530 nm处(对应HSI传感器第5波段, 简写为Band5, 下同), 而扩充至最小值10%增量后, 覆盖的波段范围为460.040~479.600 nm(Band 1—10)。 但在波长范围721.605~951.540 nm(Band 81—115), 下限浓度值已不存在。 同样地, 富营养化水体、 浑浊水体、 重金属尾矿污染水体三种自然水体背景下, 下限浓度最小值分别为: 6.30×10-2、 2.78×10-2和1.64×10-1 mg·L-1; 对应所在波长分别为: 577.865 nm(Band 46)、 587.900 nm(Band 49)、 669.285 nm(Band 70); 对应的扩充最小值10%增量后的覆盖波段范围分别为555.725~587.900 nm(Band 39—49)、 568.160~612.740 nm(Band 43—56)、 627.895~687.410 nm(Band 60—74)。 以上特征波段, 均是未来硫酸铁遥感反演模型敏感波段集合的重要参考依据。 这四种水体背景下的下限浓度最小值大小关系是: 理论清深水体<<浑浊水体<富营养化水体<重金属尾矿污染水体, 说明相比理论清深水体, 三种自然水体背景下遥感敏感性相对有所下降。 从该最小值出现的波长位置(或范围)来看, 三种自然水体背景下的下限浓度最小值所在波长相比理论清深水体均向卫星图像受大气影响作用越来越小的长波方向移动。 这个波长位置的移动方向由硫酸铁自身的吸收系数光谱和背景水体反射率光谱二者共同决定。 以上研究成果为将来实现水中硫酸铁浓度遥感反演打下了理论基础, 进一步推动水体重金属遥感领域发展。
Using satellite remote sensing technology to monitor heavy metals in water is of great research significance. However, due to the low content of heavy metals in natural water, the feasibility of remote sensing inversion is still doubted by the academic community, resulting in relatively slow development in this field. Because of this, taking the retrieval of iron sulfate concentration in water by the Chinese HJ-1A Satellite Hyperspectral Imager (HSI) as an example, the remote sensing sensitivity analysis model (DDE model) was used to numerically simulate the lower limit concentration spectrums in remote sensing inversion of iron sulfate under the background of four kinds of water, including: theoretical clear deep water and three kinds of common natural water: eutrophic water, turbid water and heavy metal polluted water. The minimum value of the remote sensing inversion lowers the limit concentration, and its wavelength is given. The variation pattern of remote sensing sensitivity under the background of different kinds of water is then analyzed. The research results found that under the background of different kinds of water, the simulated minimum lower limit concentration of iron sulfate and its wavelength position changed. Under the background of theoretically clear deep water, the minimum lower limit concentration is 4.63×10-4 mg·L-1, appearing at 468.530 nm (the fifth band of the HSI sensor, abbreviated as Band 5, the same below). After expanding to the minimum 10% increment, the covered band range is 460.040~479.600 nm (Band 1—10). However, the lower limit concentration value no longer exists in the wavelength range 721.605~951.540 nm (Band 81—115). Similarly, under the background of three kinds of natural water: eutrophic water, turbid water, and heavy metal polluted water, the minimum lower limit concentrations are: 6.30×10-2, 2.78×10-2, and 1.64×10-1 mg·L-1; the corresponding wavelengths are: 577.865 nm (Band 46), 587.900 nm (Band 49), 669.285 nm (Band 70); the corresponding coverage band ranges after expanding the minimum value by 10% are: 555.725~587.900 nm (Band 39—49), 568.160~612.740 nm (Band 43—56), 627.895~687.410 nm (Band 60—74). The above characteristic bands are all important references for the future sensitive band collection of iron sulfate remote sensing inversion models. The relationship between the minimum lower limit concentration under the background of four kinds of water is: theoretical clear deep water<<turbid water<eutrophic water<heavy metal polluted water, which shows that compared with the theoretical clear deep water, the sensitivity of remote sensing under the background of three kinds of natural water has relatively decreased. Judging from the wavelength position (or range) where the minimum value appears, the wavelengths of the minimum retrievable concentrations under the background of three kinds of natural water all move toward the longer wavelength direction where satellite images are less affected by the atmospheric influence than theoretically clear deep water. The moving direction of this wavelength position is determined by both the absorption coefficient spectrum of iron sulfate itself and the reflectance spectrum of the background water. The above research results have laid a theoretical foundation for the remote sensing inversion of iron sulfate concentration in water in the future, further promoting the development of the field of remote sensing of heavy metals in water.
水中重金属浓度监测是治理水环境污染乃至保障人类生命安全的重要手段。 相比传统人工采样监测手段, 卫星遥感技术具有覆盖范围大、 周期性重复覆盖和有助于发现与追溯污染源的优势, 将其应用在重金属参数监测具有前景和科学意义。 Chen等首先在国际地球科学与遥感大会(IGARSS)会议上提出了这个研究方向, 标志着该领域的起步[1], 随后邓孺孺、 梁业恒等人从重金属化合物光学参数测量[2, 3]、 野外金属矿区水体特征及模型精度分析[4]等方面开展了一系列的研究。 上述成果为水体重金属遥感反演领域进一步打下基础[5]。
一直以来, 学界以自然水体重金属含量低, 其光谱响应弱为由, 对能不能在卫星图像上有所体现持怀疑态度, 其遥感反演可行性一直困扰着从事相关研究的学者们, 以致该领域发展仍比较缓慢。 因此, 分析重金属遥感可行性是其中一个必需解决的科学问题。 针对这一难题, Liang等提出了一个在传感器灵敏度和背景水体状态已知的条件下, 可模拟出某种待反演的重金属化合物能引起仪器观测值变化的下限浓度计算模型, 即“ D-δ (ε) Model” (下文称作“ DDE模型”)。 该研究以硫酸铜和硫化镉为例, 成功获得了在理论清深水体背景下, 这两种化合物的遥感反演下限浓度在常用水质遥感工作波段内的光谱曲线[6]。
接下来希望进一步研究重金属在不同水质类型背景下的反演下限浓度, 并与理论清深水体背景作对比, 进而分析其可遥感的敏感性会发生怎样的变化? 而此方面正是未来在卫星层面实现其遥感反演的关键, 有关研究尚未见类似报道。
硫酸铁常见于金属尾矿废水中, 铁元素与水分子形成水合铁离子, 所以选其为研究对象, 首先采用DDE模型, 数值模拟其在理论清深水体和三种常见自然水体: 富营养化水体、 浑浊水体与重金属尾矿污染水体, 共计四种背景下可遥感反演下限浓度随波长变化的曲线, 明确地给出它的最低遥感反演浓度及其所相应的波长, 进而分析不同水体类型背景下遥感敏感性的变异规律。 为将来实现其卫星遥感层面的反演打下基础。
广东省北江流域上游区域有大宝山金属矿区和流域周边分布重金属污染型工厂, 自然河流出现重金属污染情况概率较高, 因此非常适合开展水体重金属遥感研究。 选取了表1所列的#B、 #D、 #E这三处光谱测量点, 分别代表重金属尾矿污染水体、 浑浊水体与富营养化水体三种背景水体。
| 表1 背景水体信息表 Table 1 Background water information |
1.2.1 可遥感反演下限浓度的计算方法
假设采用Deng等提出的水质遥感模型[7, 8, 9, 10]来实施水中重金属反演, 结合遥感敏感性分析DDE模型[6], 那么某种重金属化合物可遥感反演下限浓度与探测传感器灵敏度存在以下函数关系
式(1)中, D为能引起传感器原始观测值发生变化的最小浓度, 即研究的目标函数— — 重金属化合物可遥感反演的下限浓度; ε 表征仪器能分辨的最小观测值, 即探测传感器灵敏度; α HM为该重金属化合物的单位浓度吸收系数; β HM为该重金属化合物的单位浓度散射系数。 特别地, 对于可溶于水的化合物, 认为其属于分子散射, 散射作用远小于吸收作用, 即β HM≈ 0; B为背景水体的总散射系数; K为背景水体的总消光系数。
式(1)中的δ (ε )函数是表征与背景水体、 传感器探测性能参数有关的函数, 也是DDE模型之所以能建立起D与ε 的关键桥梁, 用式(2)计算
式(2)中, DN0为背景水体的探测传感器原始观测值(即Digital Number); Gain为传感器定标斜率; Offset为传感器绝对定标系数偏移量。 因为研究成果最终是为了能应用在卫星影像上, 所以选择中国环境卫星(HJ-1A)搭载的高光谱传感器(HSI)为例, 作为DDE模型的仪器参数来源。 下文的模拟结果波段显示范围, 也会重采样至和该传感器波段设置一致。
式(2)中参数的计算方式或获取方法在1.2.2和1.2.3节进一步阐述。 上述DDE模型及δ (ε )函数更详细的建模原理和数学推导过程可参考文献[6], 受篇幅限制, 这里不再赘述。
1.2.2 背景水体的探测传感器原始观测值的计算方法
式(2)背景水体的探测传感器原始观测值DN0, 可根据传感器辐射定标和辐射纠正原理, 用式(3)反算得到
式(3)中, R0为背景水体反射率; Es为大气层外太阳辐照度; θ z为太阳天顶角; d为日地平均距离因子; 若应用情景是卫星传感器, 则式(3)中的Es、 θ z、 d三个参数均可从图像数据头文件查询得到。
1.2.3 背景水体反射率的获取
式(3)背景水体反射率R0有两类情形: 理论清深水体和自然水体。
对于理论清深水体的情形, 通过Deng提出的水质遥感模型正演计算出其反射率R0, 即式(4)
式(4)中, α w为纯水吸收系数, 该值来自文献[11, 12]; β w为纯水散射系数, 该值来自文献[13]; P(Θ )为水分子散射相函数, Θ 为散射角; μ 为与测量几何有关的参数。
对于自然水体的情形, 通过开展野外实验, 选取典型水域作为测量点, 使用光谱仪现场测量得到其反射率R0。
为保持与前期研究的延续性, 实验里的三种自然水体的现场水体反射率测量结果来自参考文献[4]那次野外实验的另一组独立测量数据(每组光谱采集数量为30条)。 为便于下文对结果的分析与讨论, 样点名字、 经纬度与背景水体类型对应关系如表1所列。 实验样点更详尽的地理位置分布图、 水质化验结果以及样点离水反射率和式(1)中总散射系数和总消光系数的处理方法, 可参考文献[4]。
综上所述, 所采用的DDE模型含较多参数, 为便于理解各公式的逻辑关系, 将它们的取值/计算方法/获取方式归纳成如表2所示。
| 表2 DDE模型参数表 Table 2 Parameters of DDE model |
根据式(4)模拟得到的理论清深水体和现场测量并经处理后的三种背景水体在波长355~955 nm的反射率光谱曲线如图1所示。
 | 图1 作为DDE模型参数的四种背景水体的反射率光谱Fig.1 The reflectance spectra of four kinds of background water as DDE model parameters |
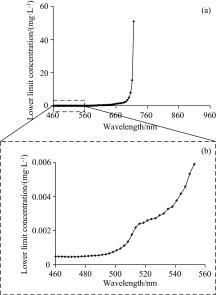
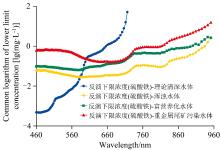
联立式(1)— 式(4), 计算得到四种水体类型背景下硫酸铁的可遥感反演下限浓度随波长变化曲线, 并将计算结果重采样与传感器HSI的波段设置一致, 如图2— 图3所示。 由于计算结果取值跨度较大, 同时采用常用对数坐标显示计算结果, 即图4。 因为下限浓度越低, 代表遥感反演的敏感性越高, 所以有应用价值的是整条曲线的低值区结果, 故将图2(a)和图3(a)的横、 纵坐标的显示区间重新调整, 将低值区放大显示, 即分别如图2(b)和图3(b)所示。 接下来在2.2节和2.3节对得到的光谱模拟结果进行特征分析。
图2是理论清深水体背景下, 计算得到的硫酸铁在不同波长下传感器观测值发生最小变化的最低浓度。 这个下限浓度是随波长变化而变化的, 而且取值跨度较大(图4)。 而在这个波长范围里, 遥感反演下限浓度光谱曲线最小值是4.63× 10-4 mg· L-1, 出现在468.530 nm处, 该波长对应HSI传感器的第5波段(简写为Band 5, 下同), 这是利用该卫星图像探测硫酸铁浓度的理论最小值。 但将来实施遥感反演时需要联立多个波段进行遥感模型的求解, 因此往往只关心单一最小值所在波长依然不足够, 应适当扩展该最小值的邻域范围, 如果认为下限浓度最小值10%增量所在的波段都可考虑为敏感波段集, 即460.040~479.600 nm(Band 1— 10), 此时便将单一最敏感波长扩充至一个适当的波长范围, 这有助于构建用于模型反演的特征波长集合。 需要说明的是, 这个增量百分比可以根据得到的波段集合的元素数量多少进行合理调整。 同时也注意到在波长范围721.605~951.540 nm(Band 81— 115), 由于理论清深水体反射率已接近于0(见图1), 尽管此情形下信息量不足以反演这种化合物, 所以这里的下限浓度均不存在, 但并不意味着这些波段在未来实施遥感反演就失去用处, 这个现象将在2.3节进一步阐述。
同样地, 从图3的计算结果, 可以得出三种自然水体背景下可遥感反演下限浓度最小值及所在波长位置, 以及最小值10%增量的波段范围。
最后将四种背景水体的敏感波长归纳成如表3。
| 表3 四种背景水体下硫酸铁的可遥感反演下限浓度最小值对比表 Table 3 Comparison of the minimum value of the lower limit concentration of iron sulfate in remote sensing inversion under the background of four kinds of water |
通过表4, 可以更直观地对比四种背景水体下硫酸铁可遥感反演下限浓度最小值及其波长位置与最小值10%增量的波长范围。
| 表4 四种背景水体下硫酸铁的可遥感反演下限浓度最小值及增量10%的波段范围对比表 Table 4 Comparison of the band range of the minimum value of the lower limit concentration and its 10% increment of iron sulfate in remote sensing inversion under the background of four kinds of water |
从图2— 图4可以发现, 硫酸铁可遥感反演下限浓度的最小值及所在波长位置并不是固定不变。 从该值的大小来看, 四者大小关系是: 理论清深水体< < 浑浊水体< 富营养化水体< 重金属尾矿污染水体。 这里需要特别指出的是: 重金属尾矿污染水体是四种背景水体中最大的, 即最“ 不敏感” 的。 这是由于该尾矿污染水体本身就含有高浓度的硫酸铁, 所以应理解为, 当硫酸铁从一个高浓度增加至另一个高浓度以至于可以被传感器观测到其变化是不容易的, 而这个类似“ 浓度分辨率” 的变化规律已证明是服从DDE模型理论[6]。 相比理论清深水体, 三种自然水体背景下该值均提高了, 说明敏感性相对有所下降, 这一现象虽然令人有点“ 失望” , 因为这正是让学界对重金属能否在自然水体光谱有所体现持有疑问的“ 理由” 。 但是, 通过DDE模型的计算, 已进一步明确地掌握了以HSI传感器为例的硫酸铁具体遥感反演下限值浓度(或浓度数量级)的取值区间。 尽管目前该传感器探测水平可能暂时不足以观测到自然水体里低浓度水平的重金属信息, 但随着光谱探测技术发展, 对于未来新一代航天航空传感器, 其探测灵敏度肯定只会越来越高, 从而使探测下限浓度最小值趋向越来越小, 亦即遥感敏感性越来越高。
从该最小值出现的波长位置(范围)来看, 它在不断变化, 这是令人振奋的现象, 并且相比于理论清深水体背景, 硫酸铁在三种自然水体的模拟结果均向图像受大气影响作用越来越小的长波方向移动。 从前期研究成果可知, 硫酸铁吸收主要在紫蓝光等短波波段[2], 而实验中三种自然水体反射峰主要在可见光长波位置[4]。 从这四种背景水体对比结果来看, 在理论清深水体背景下, 即当硫酸铁吸收作用为主导时, 该最小值便出现在可见光短波位置; 而自然水体中其他杂质的吸收作用占主导时, 该值出现在与该类水体反射最为强烈的波长位置附近。 说明这个波长位置的移动方向是由硫酸铁本身的吸收系数光谱和自然水体反射率光谱二者所共同决定的。 此外, 在理论清深水体的某些近红外波段(721.605~951.540 nm), 本该不存在的下限浓度值, 在三种自然水体背景下均重新出现。 这是由于当自然水体的水中杂质开始变得复杂时, 水中某些大颗粒杂质增加了水体后向散射能力, 使得这些波长下的反射率重新有了包含硫酸铁在内的宝贵水质信息, 当放宽最小值增量百分比后, 这些波段同样可考虑作为反演其浓度的候选敏感波段。
模拟计算了硫酸铁在理论清深水体、 浑浊水体、 富营养化水体以及重金属尾矿污染水体四种水体类型背景下可遥感反演的下限浓度光谱曲线, 给出了各自的下限浓度最小值及对应的波长位置, 并将结果进行对比分析, 进而得到变异规律。 这项研究的价值在于:
(1)DDE模型模拟出了明确的利用遥感等光谱探测技术进行硫酸铁等铁元素浓度提取的一个可观测的下限浓度光谱结果。 研究结果可使从上百个甚至几百个波段中, 大海捞针式地寻找这个“ 最佳敏感波段组合” , 缩小至一个更有效率和更具针对性的波段范围。 这对于后续反演构建敏感波段组合策略是有重要指导意义的。
(2)研究发现以硫酸铁为例的反演下限浓度是随着自然水体本身主导的光谱响应特征变化而变化的, 下限浓度的最小值及出现的波长位置由该化合物本身光学参数和背景水体反射率二者的特征所决定, 并且服从DDE模型所揭示的函数关系。
研究结果给出了可以通过遥感图像实现重金属反演的最小浓度值, 为未来判断能否实现卫星层面的水体重金属浓度监测提供理论基础和参考依据, 进一步推动了水体重金属遥感的发展。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|