为验证基于谱域插值的特征光谱提取算法的优越性和普适性, 选择中国科学院空天信息研究院张立福教授团队发布的雄安新区马蹄湾村航空高光谱影像分类标准数据集(后续统称为航空高光谱集)和安徽师范大学李虎教授团队利用ASD野外光谱仪测量的皇甫山国家森林公园树种光谱数据集(后续统称为树种光谱集)作为实验数据。 基于取算术平均值和谱域插值的方式提取特征光谱, 并利用不同的特征光谱进行分类识别和精度评价, 以验证谱域插值特征光谱提取的有效性和优越性。

航空高光谱集其光谱范围为400~1 000 nm, 波段250个, 影像大小为3 750× 1 580像元, 空间分辨率0.5 m。 数据集经过预处理流程和实地调查, 标记主要地物19类。 数据集细节信息详见参考文献[5]。 树种光谱集使用ASD野外光谱分析仪Field Spec4 Std-Res进行采集。 使用仪器波长范围为350~2 500 nm, 光谱采样间隔在350~1 000 nm为1.4 nm, 1 001~2 500 nm为1.1 nm。 测量前使用白板标定, 保证视场范围内阳光直射, 探头垂直向下, 在距离地物80 cm处探测, 每个样点测10条曲线, 平滑去噪后取均值作为样点树种的光谱。 数据集采集与处理详情可参考文献[6]。

本文计划提取谱域插值特征光谱(spectral domain interpolation characteristic spectrum, ICS)和均值特征光谱(mean characteristic spectrum, MCS)对航空高光谱集进行光谱角制图(spectral angle mapping, SAM), 对树种光谱数据集进行特征参量提取、 参量重要性评价和线性判别分析(linear discriminant analysis, LDA), 并进行精度验证和分析, 以探究ICS对目标地物整体形态的表征效果和细节特征的再现能力。 为了保证特征光谱的代表性、 实验流程的科学性和后续精度验证的可靠性, 需对数据进行预处理。

针对航空高光谱集, 需先从影像中提取出足够数量的不同地类光谱, 用于后续ICS和MCS的计算和光谱角制图。 参考前人研究^[7], 基于航空高光谱集的地类标注数据, 逐地类生成随机点并提取光谱信息, 要求每种地类生成10个随机点, 且随机点之间的距离大于50 m。 在标注的19种地类中有16种成功生成10个随机点。 3种地类因分布太少无法生成足够随机点, 故将其排除在后续分类系统内。

针对树种光谱集, 首先排除光谱样本数量在50条以下的树种, 剩余6类树种可用于后续研究。 然后将各类树种的光谱样本随机分为两部分, 30条用于特征光谱提取和构建判别模型, 20条用于构建验证集^[6]。 最后, 对纳入分类体系树种的未平均原始光谱进行整理, 方便后续利用谱域插值算法提取ICS。 实验方案构建情况如表1所示。

表1

Table 1

表1(Table 1)

表1 实验方案构建情况 Table 1 Construction of experimental schemes 名称 分类系统 参量 分类 方法 精度 验证集 航空高 光谱集 玉米、 杨树、 桃树、 裸地、 栾树、 柳树、 梨树、 国槐、 复叶槭、 白蜡、 房屋、 草地、 菜地、 水域、 水稻茬、 水稻 全波段 SAM 地类标 注数据 树种 光谱集 马尾松、 湿地松、 杉树、 朴树、 麻栎、 黄檀 8特征参量 全波段 LDA 120条 光谱

表1 实验方案构建情况 Table 1 Construction of experimental schemes

ICS的提取算法可分为4步, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 ICS计算流程Fig.1 Spectral domain interpolation characteristic spectrum extraction process

第一步, 计算谱域。 假设用N条波段数为M地物光谱计算特征光谱, 先将反射率乘于10 000化为整型便于计算, 然后将N条地物光谱构建成一个N× M的矩阵, 矩阵第n行m列的数值为第n条光谱m波段的反射率。 计算矩阵每一列的最大值max和最小值min, 构建出该目标地物的谱域空间, 即图1中蓝线代表的的谱域边界。

第二步, 构建矩阵。 构建N个10 000× M的矩阵A_i, i∈ [1, 2, …, N], 对应N条地物光谱。 矩阵每列仅1个值为1, 其余值均为0。 每列1值所在的行号即该波段反射率。 如第i条地物光谱的m波段反射率为R_m, 其对应的矩阵中A_i中第m列R_m行值为1, 该列其他值为0。

第三步, 谱域插值。 逐列计算光谱i反射率与谱域边界的距离, 即|max-R_m|、 |min-R_m|。 然后在对应的矩阵A_i中以R_m行作为中心向上下逐行递减插值, 直至值不大于0, 向上递减值为1/|max-R_m|, 向下递减值1/|min-R_m|。 完成矩阵A_i的插值更新, 得到N个10 000× M的矩阵, 称为插值谱域空间。

第四步, ICS提取。 将N个矩阵, 即插值谱域空间, 进行累加, 生成一个10 000× M矩阵, 即累计谱域空间。 然后逐列计算累计谱域空间的最大值, 记录下最大值所在的行号, 得到的1× M一维矩阵就是ICS。

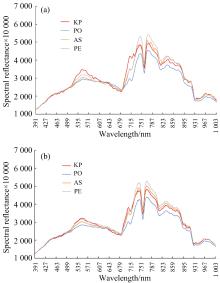
图2为航天高光谱集10条玉米光谱所提取的ICS与MCS, 在450~700 nm的谱段可以明显看出MCS对原始光谱数据起到了一个平滑的作用, 而ICS平滑效果不明显。 对于较为相似的地物光谱而言, 对于细节处的平滑可能造成细节特征的损失。 ICS能够更好地保持地物光谱的细节特征。 在700~900 nm的谱段可以看出, MCS要显著高于ICS, 这实际上是由于一条异常高的玉米光谱引起的。 这表明MCS耐抗性差, 易受到极值的影响, 而ICS受到极值的影响小, 能够更加综合、 客观地反应出地类的特征光谱。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 航空高光谱玉米ICS与MCS对比Fig.2 Comparison of corn ICS and MCS in aerospace hyperspectral image

基于传统的均值算法和1.3所提出的谱域插值算法提取MCS和ICS, 结合1.2制定的实验方案进行分类和精度验证, 以对谱域插值的特征光谱提取算法进行科学的分析评价。

1.4.1 光谱角制图

光谱角制图是一种典型的基于投影的光谱相似性度量方法, 相较于光谱幅值差异, 基于投影的光谱角制图算法更加关注光谱形态差异, 并能在一定程度上反映出光谱整体形态趋势。 因此, 基于ICS和MCS对航空高光谱数据进行光谱角制图和精度验证, 以评价谱域插值特征光谱提取算法在光谱整体形态上的表征能力。 光谱角对应待识别光谱向量s_x与参考光谱向量s_y之间的余弦夹角, L为波段总数, 计算公式如式(1)^[8]

dSAM(sx, sy)=arccos(< sx, sy> /‖sx‖×‖sy‖)=arccos∑i=1Lsxisyi/∑i=1L(sxi)21/2×∑i=1L(syi)21/2(1)

1.4.2 费雪得分

特征光谱主要由形态和幅值组成, 对特征光谱的评价还需考虑其在细节上的幅值变化。 因此利用光谱形态相似树种的ICS和MCS提取能够代表光谱幅值细节的特征参量, 并基于费雪得分(fisher score, FS)对特征参量重要性进行评价, 以探究谱域插值特征光谱提取算法在特征细节上的再现和类间可分离能力。 FS是一种经典的单变量特征评价算法, 能够对单一特征进行测试, 衡量该特征和响应变量之间的关系, 对于理解数据有较好的效果。 假定u_ij和ρ _ij分别是特征i在类别j中均值和方差, u_i为特征i的均值, n_j为类别j中的样本数。 第i个特征的得分就是FS_i就是i特征在数据集上的类间方差与类内方差的比值, 因此, FS_i越大, 证明该特征参量在数据集上的鉴别和表征能力越强。 计算公式如式(2)^[9]

FSi=∑j=1Knj(uij-ui)2/∑j=1Knjρij2(2)

1.4.3 线性判别分析

利用经过FS评价后的特征参量进行线性判别分析, 印证FS评价结果, 对ICS和MCS提取能够表征光谱特征幅值的特征参量进行分析, 并进一步对谱域插值特征光谱提取算法的有效性和优越性进行评判。

线性判别分析是一种经典的线性监督学习方法, 算法思想与FS一脉相承。 通过在数据集的特征空间内寻找一条合适的线y=w^Tx+b, 使得数据集内样本投影到该直线时类内投影点尽可能接近, 类间投影点尽可能远离, 从而根据投影位置实现类别的判定。 因此, 类比FS思想, 定义类内散度矩阵和类间散度矩阵, 并将二者的组合比值作为目标函数, 利用拉格朗日乘子法求解目标函数最小值, 以获取线性判别公式参量^[10]。

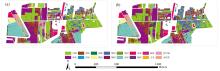
SAM是通过计算像元光谱向量的夹角来度量光谱间的相似性, 关注光谱形态的相似度, 所以SAM的精度能衡量特征光谱整体形态对目标地类的表征力。 基于上节所述流程提取到的MCS与ICS, 利用SAM进行航天高光谱集分类制图, 分类结果如图3所示。 利用航空高光谱集标注数据分层按比例生成验证像元, 利用混淆矩阵对分类结果精度进行验证, 以总体精度(overall accuracy, OA)、 Kappa系数、 制图精度(producer's accuracy, PA)和用户精度(user's accuracy, UA)作为精度指标进行评价, 结果如表2所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 均值(a)与插值(b)特征光谱SAM结果Fig.3 SAM results of mean (a) and interpolation (b) characteristic spectra

表2

Table 2

表2(Table 2)

表2 分类结果精度验证表 Table 2 Accuracy verification table of classification results 地类 UA/% PA/% OA/% Kappa ICS MCS ICS MCS ICS MCS ICS MCS 杨树(PO) 20.57 20.33 33.91 32.13 60.49 56.25 0.585 4 0.543 4 桃树(PE) 23.28 21.26 33.88 31.56 水域(WA) 92.71 82.58 96.07 97.68 裸地(BL) 95.76 96.27 85.45 93.76 栾树(KP) 32.75 23.16 42.11 33.47 柳树(WI) 33.96 20.59 57.45 35.25 梨树(PEA) 51.63 39.66 98.39 93.49 国槐(SJ) 24.52 22.21 42.12 31.59 复叶槭(AN) 26.62 20.74 29.37 28.39 房屋(BUL) 60.91 62.16 91.55 82.54 草地(GL) 83.43 81.44 52.19 53.94 菜地(VF) 78.62 68.33 22.48 22.36 白蜡(AS) 98.84 96.66 49.47 33.16 水稻(RI) 93.11 95.07 94.86 97.6 水稻茬(RS) 68.22 69.82 95.65 96.06 玉米(CO) 33.09 21.14 39.82 53.28

表2 分类结果精度验证表 Table 2 Accuracy verification table of classification results

由图3和表2可以得出以下结论。 首先, 在整体上看, 相较于传统的基于算术平均值的均值特征光谱, 基于谱域插值提取的特征光谱在进行光谱角制图时, 总体精度高4.24%, Kappa系数也领先0.042, 这表明ICS在联合光谱角制图算法进行分类时, 在精度和稳定性上都要优于传统MCS。 其次, 对比各目标地类的识别精度, 可以看出在16种地类的32个单项精度指标(PA、 UA)中, 23个为ICS表现的更加优秀。 同时, 可以看出MCS表现更好的指标主要集中在光谱特征差异比较显著, 识别难度较低的水域、 裸地、 房屋、 水稻茬等地物上。 对于光谱特征较为相近的地物, ICS表现出了较为明显的识别优势, 这也在一定程度上证明ICS能更好地保留目标地物的细节特征, 增强特征光谱对近似地物的识辨能力。 最后, 对算法产生的错分现象进行对比分析, 可以看出对于水域、 裸地、 房屋、 草地、 水稻的识别中, 光谱角制图算法取得了不错的精度。 错漏分主要发生在杨树、 桃树、 栾树白蜡等植被中。 如图4所示, 虽然ICS在535~571和715~751 nm等处光谱幅值和细节特征的类间可区分度要明显优于MCS, 但是发生错分的几类植被在整体形态上极为相似, 仅仅通过光谱向量夹角无法进行有效区分。 对于特征差异显著的地物, 基于ICS和MCS的SAM均有较好的表征识别能力, 但对于光谱形态相似的植被类型, 二者均存在明显的错分。 该现象与Wang等的研究结论一致, 表明SAM算法主要捕捉特征光谱的形态趋势, 但ICS较高的可分离度也表明了谱域插值算法对相似地物具备更好的细节捕捉能力, 识别精度较低主要归因于SAM算法对谱域变异性引起地物细节特征的区分能力有限^[11]。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 错分树种特征光谱对比图Fig.4 Characteristic spectral contrast chart of misclassification tree species

为了更好地探究不同特征光谱提取算法对目标地物细节特征和幅值的再现能力, 以光谱形态相似的ASD树种实测光谱为数据源, 参考前人研究^{[12, 13]}, 提取能够代表光谱细节特征和幅值的参量(见表3)进行FS特征重要性分析。 首先, 分别基于ICS和MCS算法提取树种特征光谱, 并按照定义提取特征参量。 然后, 对特征参量分类别进行归一化处理, 剔除不同量纲带来的影响。 最后, 利用归一化特征参量进行FS评分计算, 基于能够表征光谱幅值的特征参量FS对ICS和MCS进行评价。

表3

Table 3

表3(Table 3)

表3 特征参量定义表 Table 3 Definition table of characteristic parameters 代码 名称 定义 Db 蓝边振幅 蓝边范围内(490~530 nm), 一阶微分最大值 Sb 蓝边面积 蓝边范围内一阶微分值之和 Dy 黄边振幅 黄边范围内(550~640 nm), 一阶微分最大值 Sy 黄边面积 黄边范围内一阶微分值之和 Dr 红边振幅 红边范围内(680~760 nm), 一阶微分最大值 Sr 红边面积 红边范围内一阶微分值之和 Rg 绿峰反射率 波长510~560 nm范围内最大反射率 Rr 红谷反射率 波长650~690nm范围内最小反射率

表3 特征参量定义表 Table 3 Definition table of characteristic parameters

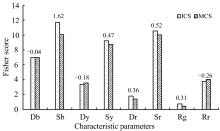
FS结果如图5所示, 直方图上方的数字标签为ICS参量FS与MCS参量FS之差。 由图可以得出以下结论。 首先, ICS和MCS幅值特征参量重要性顺序总体上保持一致, 从高到低排序均是Sb、 Sr、 Sy、 Db、 Rr、 Dy、 Dr、 Rg, 表明幅值特征的重要性和表征能力主要还是受到目标本身理化特性影响。 同时, 同类特征参量在不同特征光谱上FS差异不大于1.62, 这是因为ASD实测光谱数据都是对同类样点进行标准化的重复观测, 同一个样点的多条光谱及同类样点的光谱之间的差异相对较小。 其次, ICS幅值参量的重要性普遍优于同类型MCS幅值参量, 平均FS增加0.35。 在选定的8个幅值参量中, ICS幅值参量FS在Sb、 Sy、 Sr等5个参量上优于MCS, 且表征能力最强、 评分最高的3个幅值参量, 均是ICS占优。 表明谱域插值特征光谱提取算法相较于传统均值特征光谱, 可以更好的保留目标的特征信息, 具有更好的幅值细节再现能力。 最后, 对比各同类型幅值特征FS差异, 可以看出对于树种识别而言, 与虞佳维和王岽等对其他植被光谱分类特征的研究结论一致, 较为有效的特征参量是特征区域面积信息, 如Sb、 Sy和Sr^{[12, 14]}。 特征光谱幅值参量分析结果显示ICS对特征区域面积参量的优化效果最为明显, 表明在特征构建和分类场景中, ICS更具潜力和优势。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 特征参量FSFig.5 Fisher scores of characteristic parameters

FS作为单特征评价方法, 仅考虑单个参量与响应因子之间的关系, 虽然有助于数据理解, 但是对多参量间的相互作用关系未做考量。 为了进一步全面的对不同特征光谱细节参量进行用评价, 使用上节中评分较高的幅值参量Sb、 Sr、 Sy、 Db和Rr, 加上归一化的红边位置、 蓝边位置、 黄边位置(Dr、 Db、 Dy所对应波长)参量进行LDA分类, 并用验证集中6类120个样本进行精度评价。 同时, 使用原始均值特征光谱全波段进行LDA分类和精度验证, 以通过对比验证特征细节参量的树种表征能力和识别有效性。

将各类树种判别精度绘制为图6, 图中判别精度为该树种UA和PA的均值, 判别精度差为ICS判别精度与MCS判别精度之差, 图例括号中的值为平均判别精度差和各LDA分类的OA。 由图可得出以下结论。 首先, 相较于全波段LAD, 特征参量LAD对各个树种的识别精度都有所提高, 总体精度提升了13.93%。 表明特征光谱细节参量可以很好地表征不同树种的理化特性, 有效地降低信息冗余, 提高树种识别精度。 也证明本文使用细节参量来表征特征光谱进行分析评价具有一定的科学依据。 其次, 对比ICS和MCS特征参量LAD分类可以看出, 除在杉木上ICS特征参量判别精度低于MCS外, 其他树种的判别精度都明显优于MCS。 相较MCS, 使用ICS细节特征进行LDA分类, 平均判别精度提升2.51%, 总体精度提升2.5%, 表明通过谱域插值算法提取的特征光谱能够更好地保留目标细节特征, 更具表征能力。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 判别分析精度图Fig.6 Accuracy diagram of discriminant analysis