自适应全变差和低秩约束的高光谱图像稀疏解混

引用本文

徐晨光, 郭禹, 李峰, 刘翼, 李艳, 邓承志, 刘燕德. 自适应全变差和低秩约束的高光谱图像稀疏解混[J]. 光谱学与光谱分析, 2025,45(4): 1071-1081.
XU Chen-guang, GUO Yu, LI Feng, LIU Yi, LI Yan, DENG Chen-zhi, LIU Yan-de. Sparse Unmixing of Hyperspectral Images Based on Adaptive Total Variation and Low-Rank Constraints[J]. Spectroscopy and Spectral Analysis, 2025,45(4): 1071-1081.
Doi:10.3964/j.issn.1000-0593(2025)04-1071-11 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

自适应全变差和低秩约束的高光谱图像稀疏解混

徐晨光^1,², 郭禹¹, 李峰¹, 刘翼¹, 李艳¹, 邓承志^1,^*, 刘燕德^2,^*

1.南昌工程学院江西省水信息协同感知与智能处理重点实验室, 江西南昌 330099

2.华东交通大学智能机电创新研究院, 江西南昌 330013

*通讯作者 e-mail: 372472617@qq.com; jxliuyd@163.com

作者简介: 徐晨光, 1985年生, 华东交通大学实验师 e-mail: xcg@nit.edu.cn

收稿日期: 2024-03-17 修订日期: 2024-09-27

基金: 江西省科技厅重大科技研发专项“揭榜挂帅”制项目(20213AAG01012), 江西省2024年度研究生创新专项资金项目(YC2024-B200)资助

摘要

高光谱稀疏解混是利用一个含有丰富的端元光谱信息的光谱库作为先验, 并对高光谱数据进行分解, 得到与光谱库中各端元光谱对应的丰度的图像处理技术。然而目前大多数稀疏解混方法, 在高噪声条件下的解混效果不佳, 且很多去噪解混算法只是片面的利用了高光谱的某些特性, 并没有对高光谱特性进行全面考虑, 从而影响了解混算法的精度。为了解决这一问题, 创新地提出了一种基于自适应全变差和低秩约束的高光谱图像稀疏解混方法。首先对稀疏解混算法进行了详细的介绍, 接着对自适应全变差和低秩约束的高光谱图像稀疏解混算法进行建模, 提出自适应全变差和低秩约束的高光谱图像稀疏解混算法。该算法把高光谱数据的低秩特性和自适应TV空间特性进行了融合, 在保持丰度的低秩性和稀疏性的同时, 自适应调整丰度矩阵在不同结构下全变差正则化的水平差和垂直差比例, 达到更好的去噪效果。然后, 使用ADMM算法对新的模型进行求解。最后, 利用SUnSAL-TV, ADSpLRU, S²WSU, SU-ATV等几种比较经典的算法与本算法比较, 通过两组模拟数据和一组真实数据来实验验证算法的好坏。两组模拟数据分别是在背景单一的DC1和背景复杂的DC2中各自加入10、 15和20 dB三种高斯噪声得到的数据。模拟数据实验通过利用不同算法对这两组数据解混, 对解混结果的信号与重建误差比、丰度重构正确率和稀疏度三个数值来比较, 并对几种算法解混后的丰度图像、丰度图像与真实图像的差值图等信息进行观察对比, 从而分析几种算法的好坏。真实数据实验是利用了内华达州的Cuprite矿区高光谱真实数据对解混结果进行分析对比, 进一步用真实数据验证本算法的优势。实验结果表明: 本方法相对于较为流行的几种解混方法具有更好的鲁棒性和解混效果, 在SRE方面提高了11.4%~310.2%, 拥有更出色的性能。

关键词: 稀疏解混; 自适应全变差; 低秩约束; 高光谱图像

中图分类号:P258 文献标志码:A

Sparse Unmixing of Hyperspectral Images Based on Adaptive Total Variation and Low-Rank Constraints

XU Chen-guang^1,², GUO Yu¹, LI Feng¹, LIU Yi¹, LI Yan¹, DENG Chen-zhi^1,^*, LIU Yan-de^2,^*

1. Jiangxi Province Key Laboratory of Water Information Cooperative Sensing and Intelligent Processing, Nanchang Institute of Technology, Nanchang 330099, China

2. School of Intelligent Electromechanical Equipment Innovation Research Institute, East China Jiaotong University, Nanchang 330013, China

*Corresponding authors

Abstract

Hyperspectral sparse unmixing is an image processing technique that uses a spectral library containing rich endmember spectral information as a prior and decomposes the hyperspectral data to obtain the abundance corresponding to each endmember spectrum in the spectral library. However, most of the current sparse unmixing methods have poor unmixing effect under high noise conditions, and many de-noising unmixing methods only make partial use of some characteristics of hyperspectrum and do not fully consider the characteristics of hyperspectrum, thus affecting the accuracy of understanding the mixing algorithm. To solve this problem, an innovative hyperspectral image sparse unmixing method based on adaptive total variation and low-rank constraints is proposed. In this paper, the sparse unmixing algorithm is introduced in detail. Then, the hyperspectral image's adaptive total variation and low-rank constraint sparse unmixing algorithm are modeled. The hyperspectral image's adaptive total variation and low-rank constraint sparse unmixing algorithm is proposed. The algorithm combines the low-rank characteristics of hyperspectral data with the adaptive TV spatial characteristics. While maintaining the low rank and sparsity of abundance, it adaptively adjusts the ratio of horizontal and vertical differences of total variation regularization of the abundance matrix under different structures to achieve a better denoising effect. Then, the ADMM algorithm is used to solve the new model. Finally, several classical algorithms, such as SUnSAL-TV, ADSpLRU, S²WSU, and SU-ATV, are compared with the proposed algorithm, and two sets of simulation data and one set of real data are used to verify the quality of the algorithm. Two sets of simulation data are obtained by adding 10, 15, and 20 dB high Gaussian noise to DC1 with a single background and DC2 with a complex background, respectively. In the simulation data experiment, different algorithms were used to unmix the two data groups, and the three values of signal and reconstruction error ratio, abundance reconstruction accuracy, and sparsity of the unmixing results were compared. Moreover, the abundance image after unmixing several algorithms and the difference graph between the abundance image and the real image was observed and compared to analyze the quality of several algorithms. The real data experiment uses hyperspectral real data from a Cuprite mining area in Nevada to analyze and compare the unmixing results and further verify the advantages of the proposed algorithm with real data. The experimental results show that the proposed method improves SRE by 11.4%~310.2% with better robustness and performance than several popular methods.

Keyword: Sparse unmixing; Adaptive total variation; Low-rank constraint; Hyperspectral image

文章图片

引言

高光谱成像技术是20世纪80年代开始在多光谱遥感成像技术的基础上发展起来的^[1]。它以较高的光谱分辨率获取地物或目标的高光谱图像, 在航空、航天器上进行陆地、大气、海洋等观测中有广泛的应用^[2]。高光谱成像应用在地物精确分类^[3]、地物识别^[4]、地物特征信息的提取^[5]等诸多方面。由于高光谱成像技术的巨大优势, 成为遥感领域的一大热点, 正成为当代空间对地观测的主要技术手段^[6]。

由于受到传感器分辨率的限制以及成像地区地物分布复杂, 导致有大量混合像元存在于高光谱图像中^[7]。混合像元的存在对地面信息的分析和解译造成困扰^[8], 所以需要对获得的高光谱图像进行解混, 以获得混合像元中纯净的物质和他们对应的比例。这些纯净物质被称为端元, 对应的比例被称为丰度^[9]。

现有的高光谱混合模型主要包括线性光谱混合模型和非线性光谱混合模型两种^[10], 由于非线性光谱混合模型参数多且难以求解, 通常用线性光谱混合模型近似^[11]。在线性解混中, 目前稀疏回归算法^[12]比较常用。它借助一个庞大的光谱库作为先验知识, 加之一些正则化条件, 估算出光谱库中端元对应的丰度系数, 实现对混合像元的解混^[13]。目前比较经典且引用广泛的稀疏解混算法是由Iordache和Bioucas-Dias^[14]提出的基于分裂增广拉格朗日的稀疏解混算法(sparse unmixing via variable splitting and augmented Lagrangian, SUnSAL), 该方法为稀疏解混开辟了新的途径, 并带来了新的见解。但SUnSAL算法没有考虑到图像的空间信息, 致使其解混的稳健性不好。针对此问题, Iordache等^[15]把SUnSAL模型与全变差正则化项进行结合, 提出了基于分裂增广拉格朗日和全变差的稀疏解混算法(sparse unmixing via variable splitting augmented Lagrangian and total variation, SUnSAL-TV)。该算法利用邻域矩阵的相似性, 使得解混效果有所提升。 Zhang等^[16]在SUnSAL模型基础上, 对丰度矩阵增加了空谱约束项, 提出了一种空谱加权的高光谱稀疏解混算法(spectral-spatial weighted sparse unmixing, S²WSU), 进一步提高了解混精度。但这几种算法在高噪声条件下, 解混效果不佳。为此, 本团队对TV项进行改进, 提出基于自适应总变异化的稀疏解混算法(adaptive total variation regularized for hyperspectral sparse unmixing, SU-ATV)^[17]。该方法通过自适应调整TV正则项的水平差和垂直差的比例, 对不同结构进行自适应调整比例, 使算法的去噪性能和解混精度得到进一步提高。另外, 考虑到丰度矩阵中的向量高度相关, 使丰度矩阵表现出了低秩的特点, Giampouras等^[18]提出了同时具有稀疏性和低秩性丰度矩阵估计高光谱图像解混方法(alternating direction sparse and low-rank unmixing algorithm, ADSpLRU), 提高了解混算法的性能。

以上算法只是在稀疏、空间信息或低秩上, 片面地对高光谱数据进行解混, 而没有全面充分地利用到高光谱的特性, 为此本文把稀疏、空间信息和低秩这几个因素进行全面考虑, 提出了一种基于自适应TV和低秩约束的高光谱图像稀疏解混方法, 称为ATVLRSU。该算法一方面在稀疏解混模型的基础上融合了自适应TV, 促进图像同质区域的空间结构一致性, 另一方面融合了丰度矩阵的低秩性, 对丰度矩阵去相关, 进而达到更好的去噪效果, 提高混合像元的分解精度。

1 稀疏解混

高光谱线性光谱混合模型如式(1)

$Y = AX + N$ (1)

式(1)中, Y∈ R^l^×ⁿ表示高光谱图像, A∈ R^l^×^p表示端元光谱库, X∈ R^p^×ⁿ表示图像的丰度矩阵, N∈ R^l^×ⁿ表示高光谱图像的噪声。 l, p, n分别表示光谱波段数、端元个数和像素个数。

由于X表示为光谱库A对应的丰度系数, 是具有一定物理意义的对象丰度值, 其丰度系数应该满足丰度非负性^[19]。此外, 由于光谱库A中包含的端元个数远大于高光谱图像中真实端元的个数, 所以X丰度矩阵表现出稀疏性^[20], 于是在模型中增加了稀疏约束项和非负约束。综上所述, 线性解混模型可以表示为

$\min_{X} \frac{1}{2} ‖ AX - Y ‖_{F}^{2} + λ ‖ X ‖_{0} s.t. X \geq 0$ (2)

式(2)中, ‖ AX-Y $‖_{F}^{2}$ 为数据拟合项, ‖ · $‖_{F}^{}$ 表示Frobenius范数, λ 是控制稀疏项的权重参数, ‖ X‖ ₀为稀疏约束项, ‖ · ‖ ₀表示l₀范数, 用l₀范数来统计丰度矩阵中非零元素的个数。但由于使用l₀范数会导致求解时出现非凸优化NP(非确定性的多项式)困难问题, 于是Iordache和BioucasDias提出了SUnSAL算法^[14], 将l₀范数优化问题转化为凸优化l₁范数优化问题, 使得求解比较容易, 其模型如式(3)

$\min_{X} \frac{1}{2} ‖ Y - AX ‖_{F}^{2} + λ ‖ X ‖_{1, 1} s.t. X \geq 0$ (3)

式(3)中, $‖ X ‖_{1, 1} = \overset{p}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} | x_{i, j} | 表示 l_{1}$ 范数。

由于高光谱图像还包含丰富的空间信息, 于是Iordache等提出了SUnSAL-TV算法^[15], 在SUnSAL模型中增加了一个TV正则化项以利用图像的空间信息, 提高解混效果, 模型如式(4)

$\begin{array}{l} \min_{X} \frac{1}{2} ‖ Y - AX ‖_{F}^{2} + λ ‖ X ‖_{1, 1} + λ_{TV} TV (X) \\ s.t. X \geq 0 \end{array}$ (4)

式(4)中, λ _TV是正则化参数, 用以调整TV正则化项与其他各项的比例, $TV (X) = ‖ \nabla X ‖_{1, 1} = ||{[\begin{array}{l} \nabla_{1} X \\ \nabla_{2} X \end{array}]}_{1, 1}||$ , $\nabla_{1} X$ 是水平差分, $\nabla_{2} X$ 是垂直差分。

通常, 高光谱图像中的空间信息在不同区域拥有不同的结构^[21]。在数据形式和传输过程中, 高光谱数据不可避免的会参杂入噪声。本团队将自适应全变差(ATV)融合到高光谱解混中, 提出了自适应总变差解混模型(SU-ATV)^[17], 以更好地对解混结果去噪, 模型如式(5)

$\begin{array}{l} \min_{X} \frac{1}{2} ‖ Y - AX ‖_{F}^{2} + λ ‖ X ‖_{1, 1} + λ_{TV} ‖ T (\nabla X) ‖_{2, 1} \\ s.t. X \geq 0 \end{array}$ (5)

式(5)中, T=diag(t₁, t₂), t₁=1/(1+k| $G_{\hat{δ}}$ * ∇₁X|²), t₂=1/(1+k| $G_{\hat{δ}}$ * ∇₂X|²), k是一个调整参数, $G_{\hat{δ}}$ 是标准差, $\hat{δ}$ 的高斯卷积, ∇X=[∇₁X, ∇₂X]^T, * 是卷积符号。

由于丰度矩阵中的向量高度相关^[22], 使丰度矩阵表现出了低秩的特点, 一些方法通过引入低秩性进行约束, 以更好的地对丰度矩阵去相关, 使结果更加鲁棒。基于此, Giampouras等采用l_b_,_*范数提出了同时具有稀疏性和低秩性丰度矩阵估计高光谱图像解混模型ADSpLRU^[18]

$\begin{array}{l} \min_{X} \frac{1}{2} ‖ Y - AX ‖_{F}^{2} + λ ‖ X ‖_{1, 1} + τ ‖ X ‖_{b, *} \\ s.t. X \geq 0 \end{array}$ (6)

式(6)中, $‖ X ‖_{b, *} = \overset{rank (X)}{\sum_{i = 1}} b_{i} σ_{i} (X), b_{i} = 1 / (σ_{i} (X) + ε)$ , $σ_{i} (X)$ 表示X的奇异值。ε 是最小非负值, 用于保证分母不为零。rank(X)是X的秩。 $τ$ 是正则参数。

以上算法很好地利用了丰度的稀疏、空间信息或低秩特性, 得到了良好的解混效果, 但它们并没有把高光谱的特性全面考虑, 造成解混效果不佳。为了充分地利用高光谱稀疏、空间信息和低秩等特性, 更进一步增强解混效果, 本工作把以上几种特性进行了有效融合, 并经过大量的实验验证, 提出了一种新的自适应TV和低秩约束的高光谱图像稀疏解混算法。

2 稀疏解混算法

2.1 基于自适应TV和低秩约束的高光谱稀疏解混

高光谱图像中的空间信息在不同区域拥有不同的结构, 为了自适应调整丰度矩阵在不同结构下TV的水平差和垂直差并且保持丰度的低秩性和稀疏性, 达到更好的去噪和解混效果, 把高光谱的稀疏、低秩与自适应TV性质进行融合, 提出了自适应TV和低秩约束的高光谱图像稀疏解混算法(ATVLRSU)。具体解混模型表示如式(7)

$\begin{array}{l} \min_{X} \frac{1}{2} ‖ Y - AX ‖_{F}^{2} + λ ‖ X ‖_{1, 1} + λ_{TV} ‖ T (\nabla X) ‖_{2, 1} + \\ λ_{WT} ‖ X ‖_{b, *} + τ_{R +} (X) \end{array}$ (7)

式(7)中, ‖ AX-Y $‖_{F}^{2}$ 为数据拟合项, 使解混结果与真实值更加逼近; ‖ X‖ _{1, 1}为稀疏约束项, 用于在解混过程中对丰度矩阵稀疏性进行约束; ‖ T(∇X)‖ _{2, 1}为自适应TV项, 用于在每次迭代中自适应调整丰度矩阵在不同结构下TV的水平差和垂直差的比重, 达到更好的去噪效果; ‖ X‖ _b_,_*为低秩项, 用于对丰度矩阵去相关, 使结果更加鲁棒; τ _R+(X)表示X≥ 0, 用于对丰度矩阵非负性规范。 λ , λ _TV, λ _WT为正则化参数, 用于调节稀疏约束项、自适应TV约束项和低秩约束项的权重比例。当λ _TV=0时, 算法只考虑低秩而忽略高光谱的空间结构, 式(7)就变成了ADSpLRU算法(6); 当λ _WT=0时算法只考虑空间结构而忽略低秩, 式(7)就变成了SU-ATV算法(5); 当λ _TV=0并且λ _WT=0时, 式(7)就变成了SUnSAL算法(3)。通常在计算时, 高光谱的空间结构信息和低秩信息都要兼顾, 一般两个参数不会同时为0。在式(7)中

$\begin{array}{l} ‖ T (\nabla X) ‖_{2, 1} = ‖ diag (t_{1}, t_{2}) (\nabla_{1} X, \nabla_{2} X) {‖^{T}}_{2, 1} = \\ {||\begin{array}{l} t_{1} \nabla_{1} X \\ t_{2} \nabla_{2} X \end{array}||}_{2, 1} = {||\sqrt[]{(t_{1} \nabla_{1} {X)}^{2} + (t_{2} \nabla_{2} {X)}^{2}}||}_{1} \end{array}$ (8)

式(8)中, T=diag(t₁, t₂), t₁=1/(1+k| $G_{\hat{δ}}$ * ∇₁X|²), t₂=1/(1+k| $G_{\hat{δ}}$ * ∇₂X|²), k是一个调整参数, $G_{\hat{δ}}$ 是标准差, $\hat{δ}$ 的高斯卷积, ∇X=[∇₁X, ∇₂X]^T, * 是卷积符号。由于每次迭代更新丰度X都会发生改变, 因此在每次迭代过程中, t₁, t₂都会随着X的更新而自适应变化, 达到优化后的自适应的差分比。式(7)中 $‖ X ‖_{b, *} = \overset{rank (X)}{\sum_{i = 1}} b_{i} σ_{i} (X), b_{i} = 1 / (σ_{i} (X) + ε)$ 表示低秩项, 其中 $σ_{i} (X)$ 表示 $X$ 的奇异值。 $ε$ 是最小非负值, 用于保证分母不为零。 $rank (X)$ 是 $X$ 的秩。

2.2 模型求解

我们用交替方向乘子法(ADMM)^[23]来对模型进行求解, 过程如式(9)

令

$\begin{array}{l} g (X, V) = \frac{1}{2} ‖ Y - V_{1} ‖_{F}^{2} + λ ‖ V_{2} ‖_{1, 1} + λ_{TV} ‖ V_{5} ‖_{2, 1} + \\ λ_{WT} ‖ V_{6} ‖_{b, *} + τ_{R +} (V_{7}) \end{array}$ (9)

式(9)中: V₁=AX, V₂=X, V₃=X, V₄=∇V₃, V₅=TV₄, V₆=X, V₇=X, V=[V₁, V₂, V₃, V₄, V₅, V₆, V₇]。

可以得到

$\min_{X, V} g (X, V) s.t. GX - BV = 0$ (10)

式(10)中: G[A, I, I, 0, 0, I, I]^T, B=[I 0 0 0 0 0 0; 0 I 0 0 0 0 0; 0 0 I 0 0 0 0; 0 0-∇I 0 0 0; 0 0 0-T I 0 0; 0 0 0 0 0 I 0; 0 0 0 0 0 0 I]。 G和B为关系矩阵, 且满足GX=BV。为了解决这个问题, 我们使用拉格朗日乘数法来计算, 可以得到

$\begin{aligned} L(\boldsymbol{X}, \quad \boldsymbol{V}, \quad \boldsymbol{D})= & \min _{\boldsymbol{X}} \frac{1}{2}\left\|\boldsymbol{Y}-\boldsymbol{V}_{1}\right\|_{F}^{2}+\lambda\left\|\boldsymbol{V}_{2}\right\|_{1, 1}+ \\ & \lambda_{\mathrm{TV}}\left\|\boldsymbol{V}_{5}\right\|_{2, 1}+\lambda_{\mathrm{wT}}\left\|\boldsymbol{V}_{6}\right\|_{b, *}+\tau_{\mathrm{R}+}(\boldsymbol{V})+ \\ & \frac{\mu}{2}\left\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{V}_{1}-\boldsymbol{D}_{1}\right\|_{F}^{2}+\frac{\mu}{2} \| \boldsymbol{X}-\boldsymbol{V}_{2}- \\ & \boldsymbol{D}_{2}\left\|{ }_{F}^{2}+\frac{\mu}{2}\right\| \boldsymbol{X}-\boldsymbol{V}_{3}-\boldsymbol{D}_{3}\left\|_{F}^{2}+\frac{\mu}{2}\right\| \nabla \boldsymbol{V}_{3} \\ & -\boldsymbol{V}_{4}-\boldsymbol{D}_{4}\left\|\stackrel{2}{F}+\frac{\mu}{2}\right\| \boldsymbol{T}-\boldsymbol{V}_{5}-\boldsymbol{D}_{5} \|{ }_{F}^{2}+ \\ & \frac{\mu}{2}\left\|\boldsymbol{X}-\boldsymbol{V}_{6}-\boldsymbol{D}_{6}\right\| \stackrel{2}{F}+\frac{\mu}{2} \| \boldsymbol{X}-\boldsymbol{V}_{7}- \\ & \boldsymbol{D}_{7} \| \stackrel{2}{F} \end{aligned}$(11)

式(11)中, X, V, D为拉格朗日乘子, D=[D₁, D₂, D₃, D₄, D₅, D₆, D₇]为拉格朗日乘数法误差项, 在k+1次迭代中, 我们可以得到: $D_{1}^{k + 1}$ = $D_{1}^{k}$ -AX^k⁺¹+ $V_{1}^{k + 1}$ , $D_{2}^{k + 1}$ = $D_{2}^{k}$ -X^k⁺¹+ $V_{2}^{k + 1}$ , $D_{3}^{k + 1}$ = $D_{3}^{k}$ -X^k⁺¹+ $V_{3}^{k + 1}$ , $D_{4}^{k + 1}$ = $D_{4}^{k}$ -∇ $V_{3}^{k + 1}$ + $V_{4}^{k + 1}$ , $D_{5}^{k + 1}$ = $D_{5}^{k}$ -T $V_{4}^{k + 1}$ + $V_{5}^{k + 1}$ , $D_{6}^{k + 1}$ = $D_{6}^{k}$ -X^k⁺¹+ $V_{6}^{k + 1}$ , $D_{7}^{k + 1}$ = $D_{7}^{k}$ -X^k⁺¹+ $V_{7}^{k + 1}$ 。具体的执行伪代码见表1。

表1 ATVLRSU算法伪代码 Table 1 The pseudo-code of ATVLRSU

Algorithm1: ATVLRSU
1. Initialize:
k=0, μ > 0, λ _TV=0, λ _WT=0, X⁰=(A^TA+4I)^-1(A^TY), $V_{1}^{0}$ =AX⁰, $V_{2}^{0}$ =X⁰, $V_{3}^{0}$ =X⁰, $V_{4}^{0}$ =∇ $V_{3}^{0}$ , $V_{5}^{0}$ =T $V_{4}^{0}$ , $V_{6}^{0}$ =X⁰, $V_{7}^{0}$ =X⁰,
[ $D_{1}^{0}$ , $D_{2}^{0}$ , $D_{3}^{0}$ , $D_{4}^{0}$ , $D_{5}^{0}$ , $D_{6}^{0}$ , $D_{7}^{0}$ ]=0
2. Repeat:
(1) Update variables:
X^k⁺¹=arg $\min_{X}$ ‖ AX- $V_{1}^{k}$ - $D_{1}^{k} ‖_{F}^{2}$ +‖ X- $V_{2}^{k}$ - $D_{2}^{k} ‖_{F}^{2}$ +‖ X- $V_{3}^{k}$ - $D_{3}^{k} ‖_{F}^{2}$ +‖ X- $V_{6}^{k}$ - $D_{6}^{k} ‖_{F}^{2}$ +‖ X- $V_{7}^{k}$ - $D_{7}^{k} ‖_{F}^{2}$ ,
$V_{1}^{k + 1}$ =arg $\min_{V_{1}} \frac{1}{2}$ ‖ V₁-Y $‖_{F}^{2}$ + $\frac{μ}{2}$ ‖ AX^k⁺¹-V₁- $D_{1}^{k} ‖_{F}^{2}$ , $V_{2}^{k + 1}$ =arg $\min_{V_{2}}$ λ ‖ V₂‖ _{1, 1}+ $\frac{μ}{2}$ ‖ X^k⁺¹-V₂- $D_{2}^{k} ‖_{F}^{2}$ ,
$V_{3}^{k + 1}$ =arg $\min_{V_{3}}$ ‖ ∇V₃- $V_{4}^{k}$ - $D_{4}^{k} ‖_{F}^{2}$ +‖ X^k⁺¹-V₃- $D_{3}^{k} ‖_{F}^{2}$ , $V_{4}^{k + 1}$ =arg $\min_{V_{4}}$ ‖ ∇ $V_{3}^{k + 1}$ -V₄- $D_{4}^{k} ‖_{F}^{2}$ +‖ TV₄- $V_{5}^{k}$ - $D_{5}^{k} ‖_{F}^{2}$ ,
$V_{5}^{k + 1}$ =arg $\min_{V_{5}}$ λ _TV‖ V₅‖ _{2, 1}+ $\frac{μ}{2}$ ‖ T $V_{4}^{k + 1}$ -V₅- $D_{5}^{k} ‖_{F}^{2}$ , $V_{6}^{k + 1}$ =arg $\min_{V_{6}}$ λ _WT ${V_{6}}_{b, }$ + $\frac{μ}{2}$ ‖ X^k*⁺¹-V₆- $D_{6}^{k} ‖_{F}^{2}$ ,
$V_{7}^{k + 1}$ =arg $\min_{V_{7}}$ i_R₊(V₇)+ $\frac{μ}{2}$ ‖ X^k⁺¹-V₇- $D_{7}^{k} ‖_{F}^{2}$
(2) Update Lagrangian operators:
$D_{1}^{k + 1}$ = $D_{1}^{k}$ -AX^k⁺¹+ $V_{1}^{k + 1}$ , $D_{2}^{k + 1}$ = $D_{2}^{k}$ -X^k⁺¹+ $V_{2}^{k + 1}$ , $D_{3}^{k + 1}$ = $D_{3}^{k}$ -X^k⁺¹+ $V_{3}^{k + 1}$ , $D_{4}^{k + 1}$ = $D_{4}^{k}$ -∇ $V_{3}^{k + 1}$ + $V_{4}^{k + 1}$ ,
$D_{5}^{k + 1}$ = $D_{5}^{k}$ -T $V_{4}^{k + 1}$ + $V_{5}^{k + 1}$ , $D_{6}^{k + 1}$ = $D_{6}^{k}$ -X^k⁺¹+ $V_{6}^{k + 1}$ , $D_{7}^{k + 1}$ = $D_{7}^{k}$ -X^k⁺¹+ $V_{7}^{k + 1}$
3. Update the iteration: k=k+1 until the stop conditions are met.

表1 ATVLRSU算法伪代码 Table 1 The pseudo-code of ATVLRSU

根据 ADMM 交替迭代进行求解, 可以得到

$X^{k + 1} = (A^{T} {A + 4 I)}^{- 1} [A^{T} (V_{1}^{k} + D_{1}^{k}) + (V_{2}^{k} + D_{2}^{k}) + (V_{3}^{k} + D_{3}^{k}) + (V_{6}^{k} + D_{6}^{k}) + (V_{7}^{k} + D_{7}^{k})]$ (12)

$V_{1}^{k + 1} = \frac{1}{1 + μ} Y + \frac{μ}{1 + μ} (A X^{k + 1} - D_{1}^{k})$ (13)

$V_{2}^{k + 1} = soft (X^{k + 1} - D_{2}^{k}, \frac{λ}{μ})$ (14)

$V_{3}^{k + 1} = F^{- 1} [\frac{FFT [(X^{k + 1} - D_{3}^{k}) - div (V_{4}^{k} - D_{4}^{k})]}{FFT [I - div \nabla]}]$ (15)

其中FFT和F^-1(·)分别表示傅里叶的正反变换。

$V_{4}^{k + 1} = {[\begin{array}{l} V_{41}^{(k + 1)} & V_{42}^{(k + 1)} \end{array}]}^{T} = {[\begin{array}{l} \frac{1}{t_{1}^{2} + 1} [\begin{array}{l} \nabla_{1} V_{3}^{(k + 1)} - D_{41}^{(k)} + \\ t_{1} (V_{51}^{(k)} + D_{51}^{(k)}) \end{array}] & \frac{1}{t_{2}^{2} + 1} [\begin{array}{l} \nabla_{2} V_{3}^{(k + 1)} - D_{42}^{(k)} + \\ t_{2} (V_{52}^{(k)} + D_{52}^{(k)}) \end{array}] \end{array}]}^{T}$ (16)

$V_{5}^{k + 1} = soft (T V_{4}^{k} - D_{5}^{k}, \frac{λ_{TV}}{μ})$ (17)

$V_{6}^{k + 1} = soft (X^{k + 1} - D_{6}^{k}, (\frac{λ_{WT}}{μ}) b)$ (18)

$V_{7}^{k + 1} = \max (X^{k + 1} - D_{7}^{k}, 0)$ (19)

3 实验结果与讨论

通过以下几个实验, 将实验结果与几种目前较为流行的算法SunSAL-TV^[15]、 ADSpLRU^[18]、 SU-ATV^[17]、 S²WSU^[16]比较, 用以验证提出算法的性能优势。我们采用信号与重建误差比(signal reconstruction error, SRE)^[24]表示环境噪声进行定量分析, 其定义如式(20)

$SRE (dB) = 10 lo g_{10} [E (‖ X ‖_{2}^{2}) / E (‖ X - \hat{X} ‖_{2}^{2})]$ (20)

式(20)中, E(·)是期望值, $\hat{X}$ 是丰度矩阵的估计值, 同时, 我们引入另一个评定指标丰度重构正确率^[25]

$p_{s} = P (‖ X - \hat{X} ‖^{2} / ‖ X ‖^{2} \leq t h)$ (21)

式(21)中, P(·)假设定义阈值th=10且重构正确率p_s=1, 则意味着丰度估计的误差小于1/10, 文献[17]对于阈值的确定给出了说明: 当‖ X- $\hat{X}$ ‖ ²/‖ X‖ ²≤ 3.16(5 dB)时, 则说明丰度估计的结果是成功的, 即重构正确率为100%。通常来说SRE(dB)和p_s越大, 则解混的精度越高。

由于高光谱图像中包含的端元个数远大于高光谱图像中真实端元的个数, 所以丰度矩阵表现出稀疏性, 因此我们引入稀疏度^[27]作为第三个评定指标

$sparsity = \frac{‖ \max (\hat{X} - 0.005, 0) ‖_{0}}{p \times n_{1} \times n_{2}}$ (22)

式(22)中, $\hat{X}$ ∈ $R^{n_{1} \times n_{2} \times p}$ , p, n₁, n₂表示三个维度, 通常来说稀疏度越小, 则解混的结果越好^[29]。

3.1 模拟高光谱数据实验

为了验证本文提出的基于自适应TV和低秩约束的高光谱图像稀疏解混方法(ATVLRSU)的有效性, 在模拟数据实验中, 我们把经典的SUnSAL-TV算法^[15], 具有空谱加权约束的S²WSU算法^[16], 具有低秩性的稀疏性解混算法ADSpLRU算法^[18]和具有自适应TV的稀疏解混算法SU-ATV算法^[17]与融合了稀疏、自适应TV和低秩功能的本文提出的ATVLRSU算法进行多方面的比较。选择了高光谱数据集1(DC1)和高光谱数据集2(DC2)进行模拟实验以检验本文提出的ATVLRSU算法解混效果。为了更有效的证明ATVLRSU算法的效果, 我们准备了背景比较单一DC1模拟解混实验和背景较为复杂的DC2模拟实验共同验证我们的算法的解混效果。 DC1和DC2都利用了A∈ R^{224× 240}作为光谱库。该光谱库选自于具有权威性的美国地质勘探局(United States Geological Survey, USGS)端元光谱库^[28], 并在USGS端元光谱库中随机挑选240条光谱曲线作为模拟数据实验的光谱库。光谱波段数选取了224个, 波长在0.4~2.5 μ m的范围内均匀分布。这两组高光谱数据设定了不同的端元丰度, 图1表示DC1中五种端元的真实丰度分布图像, 丰度图像为75× 75像素。其生成过程可以参考文献[15]。图2是DC2中九种端元的真实丰度分布图像, 丰度图像为100× 100像素。两组真实高光谱数据根据线性混合模型(1), 添加10、15和20 dB三种不同信噪比的高斯噪声生成三种不同的带噪高光谱模拟数据。

	Figure Option View Download New Window
	图1 DC1的真实丰度图Fig.1 True abundance maps of DC1

	Figure Option View Download New Window
	图2 DC2的真实丰度图Fig.2 True abundance maps of DC2

在不同的信噪比下, 几种不同算法(SUnSAL-TV, SU-ATV, ADSpLRU, S²WSU, ATVLRSU)对DC1和DC2两组数据在最优参数下的解混结果和对应的参数值展示在表2和表3中, 并且在表中对同一信噪比下的解混效果最好的数值用黑体标出。

表2 DC1的解混结果 Table 2 Unmixing results of DC1

表3 DC2的解混结果 Table 3 Unmixing results of DC2

通过对两组实验结果分析, 得到结论如下: (1)使用了自适应TV正则化项的解混算法(SU-ATV、 ATVLRSU)解混效果要优于没有使用的算法(SunSAL-TV、 ADSpLRU、 S²WSU), 特别是在15 dB的DC1数据, SU-ATV和ATVLRSU解混结果SRE值是其他算法的2倍以上, 这说明自适应TV能更好地调节不同结构下的空间信息, 使解混结果更好。 (2)在含有自适应TV正则化项的解混算法(SU-ATV、 ATVLRSU)中, 加入低秩约束项的稀疏解混模型ATVLRSU比没有使用低秩约束项的解混模型SU-ATV, 解混效果提升明显。例如在20dB的DC1数据里, ATVLRSU算法比SU-ATV的SRE提高了20%以上。这说明, 低秩能够更有效的对解混结果去相关, 使解混结果鲁棒性更好。 (3)在高噪声条件下(10 dB), ATVLRSU算法的解混效果远好于其他算法, 特别是在DC1数据中, SRE提升比例高达35.7%~310.2%, DC2数据也提高了11.4%~137.7%以上。这说明融合了自适应TV、低秩和稀疏特性的本算法在高噪声条件下对于其他几种高光谱解混方法具有明显的优势。 (4)两个实验相比, 背景比较单一的DC1实验比背景较为复杂的DC2实验效果好很多, 这说明自适应TV正则化方法能够更有效的对空间信息比较简单的DC1数据进行自动空间信息调节, 达到更好的去噪目的。

为了更直观的展示不同模型的解混效果, 将五种算法对两组高光谱数据(DC1和DC2)的丰度估计图(图3)、估计图与真实值的差值图(图4)进行比较。图3中展现了同一信噪比下(SNR=20), DC1中第五个端元(EM5)的真实丰度图和五种算法最优解混丰度估计图, 相关参数见表2。可以看到, 对比其他的算法, ATVLRSU和SUnSAL-TV算法噪声点最少, 但SUnSAL-TV过于平滑与真实值偏离较大, 例如解混丰度图的第二行的最后的两个正方形丰度误差严重。图4是在相同信噪比下, DC1数据实验中几种算法的最优解混结果(见图3)的丰度值与真实值的差值图, 用于比较每种算法结果与真实值的差距, 图中颜色越蓝差值就越小, 颜色越红差值就越大。图中差值较大的图像用红色方框着重显示。对比五种算法的差值图像, 其中SUnSAL-TV、 ADSpLRU的差值明显过大, 而其他三种算法的图像中, 本文提出的ATVLRSU算法误差最小, 体现了ATVLRSU算法在稀疏解混模型基础上融合了自适应TV和低秩特性的积极的去噪作用。

	Figure Option View Download New Window
	图3 真实丰度图与不同算法对20 dB的DC1的解混估计丰度图Fig.3 True abundance maps and estimated abundance maps of DC1 by five methods under 20 dB

	Figure Option View Download New Window
	图4 DC1在20 dB时不同算法估计值与真实值的丰度差值图Fig.4 Difference maps between true abundances and estimated abundances of DC1 by five methods under 20 dB

图5是DC2数据第五个端元(EM5)的真实丰度图与五种算法对SNR为20 dB的DC2数据的最优解混估计丰度图, 相关参数是体现在表3中的20 dB一列。结合图6中五种算法对DC2数据的最优解混估计丰度(图5)与真实丰度的差值图(图中差值较大的图像用红色方框着重显示), 可以得到和上述DC1相同的实验结果, 即本文提出的算法估算结果与真实丰度图最为相似。表现出更好鲁棒性能和抗噪声性能, 解混精度最高。

	Figure Option View Download New Window
	图5 真实丰度图与不同算法对20 dB的DC2的解混估计丰度图Fig.5 True abundance maps and estimated abundance maps of DC2 by five methods under 20 dB

	Figure Option View Download New Window
	图6 DC2在20 dB时不同算法估计值与真实值的丰度差值图Fig.6 Difference maps between true abundances and estimated abundances of DC2 by five methods under 20 dB

为了更全面的展示各算法的性能, 我们把解混后所有端元的丰度图像进行比较, 由于像素过多造成图片太大, 我们随机选取了100个像素。图7是DC1和DC2在20 dB的情况下, 经过五种算法的最佳解混结果估算的丰度图(相关参数选取见表2和表3)。在图中, 差异较明显的已经用红色矩形框住。可以看出, DC1和DC2两个实验中SUnSAL-TV, ADSpLRU和S²WSU算法的图像中出现了明显的噪声, 端元的丰度受到干扰, 而SU-ATV和ATVLRSU的抗噪声效果较好, 在DC1中这两个算法几乎都看不出明显噪声, 说明加了自适应TV的算法具有其他算法不可替代的去噪性能。而在DC2实验中, SU-ATV中噪声点比ATVLRSU算法多, 融合了低秩特性的ATVLRSU算法表现比SU-ATV要好, 说明了低秩性能更进一步加强了解混结果的鲁棒性。因此, ATVLRSU算法因为融合了稀疏、自适应TV和低秩的优点, 更进一步提升了解混的精度, 解混图像与真实图像最为接近。

	Figure Option View Download New Window
	图7 真实丰度图与不同算法在20 dB时对两组数据解混丰度估计图Fig.7 True abundance maps and estimated abundance maps of DC1 and DC2 by five methods under 20 dB

结合以上几组实验的比较结果, 可以得出融合了低秩和自适应TV的稀疏解混模型ATVLRSU在促进图像同质区域的空间结构一致性和提升混合像元精度方面具有很好的效果, 使解混效果有了进一步提高。

3.2 真实高光谱实验数据

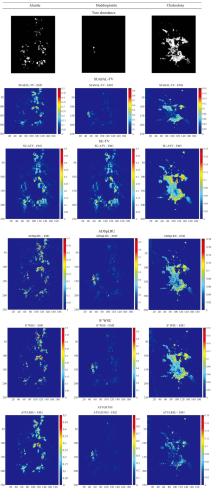
在本节中, 我们将使用广泛用于高光谱遥感图像分析的机载可见红外成像光谱仪(AVIRIS)于1995年采集的内华达州的Cuprite矿区数据^[27]作为真实高光谱进行比较和分析。图8显示了美国地质调查局(USGS)于1995年利用ricorder3.3软件^[29]制作的矿物分类图, 利用该软件产品来反映Cuprite矿区数据中各矿物的分布情况。矿区原始图像有224个波段, 波长范围为370~2 480 nm, 空间分辨率为20 m, 光谱分辨率为10 nm。实验图像使用了原始图像的部分场景, 像素大小为250× 191。在去除了由不同干扰因素影响的波段后^[27], 仅留下188个光谱波段。我们将几种不同的稀疏解混算法的丰度估计图进行比较, 并对他们的性能进行分析。

如图9, 我们分别利用SUnSAL-TV、 SU-ATV、 ADSpLRU、 S²WSU、 ATVLRSU几种算法对矿区高光谱数据进行稀疏解混。估计出明矾(Alunite)、水铵长石(Buddingtonite)、玉髓(Chalcedony)三种物质的分布情况, 即三种端元的丰度图像, 并把他们同真实值(True abundances)进行定性比较。几种解混算法的参数是通过大量仔细调参把解混结果与参考真实丰度比较取与之最接近的解混值而得到的。其值分别是SUnSAL-TV(λ =0.02, λ _TV=0.02)、 SU-ATV(λ =0.05, λ _TV=0.1)、 ADSpLRU(λ =20, λ _TV=0.05)、 S²WSU(λ =0.5)、 ATVLRSU(λ =0.05, λ _TV=0.05, λ _WT=1)。

	Figure Option View Download New Window
	图8 内华达州 Cuprite 数据中各矿物的分布情况Fig.8 Mineral map of cuprite, Nevada derived from AVIRIS Data

	Figure Option View Download New Window
	图9 几种算法对Cuprite数据的解混丰度图Fig.9 Abundance maps of Cuprite data estimated by five methods

图9中, 像元丰度值较大的地方(如红色、黄色、绿色)为矿物存在较集中的地方。为了方便比较, 解混丰度结果图与真实丰度图差异较大的作者用红色方框着重显示。从图9可以看出, 这五种算法解混结果与真实值都比较接近, 表明了这几种稀疏解混算法的有效性。但细致看来, SUnSAL-TV算法出现了过平滑的现象(例如: 明矾Alunite和玉髓 Chalcedony), 导致图像模糊, 精确度低。 SU-ATV解混效果要优于SUnSAL-TV, 但依旧存在一些过平滑问题(例如: 玉髓 Chalcedony)。 ADSpLRU的图像出现了水铵长石Buddingtonite丰度偏差较大的情况。 S²WSU解混结果中玉髓Chalcedony丰度图像中左上角有明细的错误。而我们提出的ATVLRSU与真实值最为接近。总的来说, 通过Cuprite矿区真实数据实验得出的定性结果表明, ATVLRSU算法具有很好的解混效果, 与其他几种算法比较, 其抗噪性能和精确度都有很大的提高。

4 结论

提出了一种新的基于自适应TV和低秩约束的高光谱图像稀疏解混算法, 该算法一方面在稀疏解混模型的基础上融合了自适应TV, 促进图像同质区域的空间结构一致性, 另一方面融合了丰度矩阵的低秩特性, 对丰度矩阵去相关, 进而达到去噪和提高解混精度的目的。在模拟和真实数据实验中, 将SUnSAL-TV、 SU-ATV、 ADSpLRU、 S²WSU和ATVLRSU算法进行了详细地分析和对比。实验结果证明ATVLRSU算法在信号与重建误差比方面提高了11.4%~310.2%, 具有很好的解混效果。后期我们将对算法的运算效率进行优化和运用场景进行拓展。

参考文献

文献列表

[1]	Fauvel M, Tarabalka Y, Benediktsson J A, et al. Proceedings of the IEEE, 2012, 101(3): 652. [本文引用:1]
[2]	Lu B, Dao P D, Liu J G, et al. Remote Sensing, 2020, 12(16): 2659. [本文引用:1]
[3]	Yadav C S, Pradhan M K, Gangadharan S M P, et al. Electronics, 2022, 11(17): 2799. [本文引用:1]
[4]	Cui Qiang, Yang Baohua, Liu Biyun, et al. Agriculture, 2022, 12(8): 1085. [本文引用:1]
[5]	Ma Ping, Ren Jinchang, Zhao Huimin, et al. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5508912. [本文引用:1]
[6]	Mukundan A, Huang C C, Men T C, et al. Sensors, 2022, 22(16): 6231. [本文引用:1]
[7]	Chen Jie, Zhao Min, Wang Xiuheng, et al. IEEE Signal Processing Magazine, 2023, 40(2): 61. [本文引用:1]
[8]	WU Hu-lin, DENG Xian-ming, ZHANG Tian-cai, et al(吴护林, 邓贤明, 张天才, 等). Spectroscopy and Spectral Anaysis(光谱学与光谱分析), 2024, 44(1): 283. [本文引用:1]
[9]	Ye Chuanlong, Liu Shanwei, Xu Mingming, et al. International Journal of Remote Sensing, 2022, 43(12): 4331. [本文引用:1]
[10]	Amigo J M, Babamoradi H, Elcoroaristizabal S. Analytica Chimica Acta, 2015, 896: 34. [本文引用:1]
[11]	CHEN Lei, GUO Yan-ju, GE Bao-zhen(陈雷, 郭艳菊, 葛宝臻). Acta Electronica Sinica(电子学报), 2017, 45(2): 337. [本文引用:1]
[12]	Ren Longfei, Hong Danfeng, Gao Lianru, et al. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5500415. [本文引用:1]
[13]	Wang S, Huang T Z, Zhao X L, et al. Journal of Computational and Applied Mathematics, 2023, 421: 114843. [本文引用:1]
[14]	Iordache M D, Bioucas-Dias J M, Plaza A. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2014. [本文引用:2]
[15]	Iordache M D, Bioucas-Dias J M, Plaza A. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4484. [本文引用:5]
[16]	Zhang Shaoquan, Li Jun, Li Hengchao, et al. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3265. [本文引用:3]
[17]	Ma Mingxi, Xu Chenguang, Zhang Jun, et al. Infrared Physics & Technology, 2022, 127: 104362. [本文引用:5]
[18]	Giampouras P V, Themelis K E, Rontogiannis A A, et al. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4775. [本文引用:4]
[19]	Boulais A, Berné O, Faury G, et al. Astronomy & Astrophysics, 2021, 647: A105. [本文引用:1]
[20]	Wang Jinju, Huang Tingzhu, Jie Huang, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(12): 5009. [本文引用:1]
[21]	Pang Zhifeng, Zhang Huili, Luo Shuosheng, et al. Signal Processing, 2020, 167: 107325. [本文引用:1]
[22]	Han H, Wang G X, Wang M Z, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 5704. [本文引用:1]
[23]	Rasti B, Koirala B, Scheunders P, et al. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5504615. [本文引用:1]
[24]	Wang Dan, Shi Zhenwei, Cui Xudong. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1348. [本文引用:1]
[25]	Sun Le, Ge Weidong, Chen Yunjie, et al. International Journal of Remote Sensing, 2018, 39(19): 6037. [本文引用:1]
[26]	Yuan Yuan, Dong Le, Li Xue-long. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1. [本文引用:1]
[27]	Clark R N, Swayze G A, Livo K E, et al. Journal of Geophysical Research: Planets, 2003, 108(E12): 5131. [本文引用:3]
[28]	Xu Chenguang, Wu Zhaoming, Li Fan, et al. Infrared Physics & Technology, 2021, 112: 103564. [本文引用:1]
[29]	Wang R, Li H C, Liao W, et al. IGARSS 2016 IEEE International Geoscience and Remote Sensing Symposium, 2016, 1: 6986. [本文引用:2]

2012

0.0

... 引言高光谱成像技术是20世纪80年代开始在多光谱遥感成像技术的基础上发展起来的^[1] ...

2020

0.0

... 它以较高的光谱分辨率获取地物或目标的高光谱图像, 在航空、航天器上进行陆地、大气、海洋等观测中有广泛的应用^[2] ...

2022

0.0

... 高光谱成像应用在地物精确分类^[3]、地物识别^[4]、地物特征信息的提取^[5]等诸多方面 ...

2022

0.0

... 高光谱成像应用在地物精确分类^[3]、地物识别^[4]、地物特征信息的提取^[5]等诸多方面 ...

2023

0.0

... 高光谱成像应用在地物精确分类^[3]、地物识别^[4]、地物特征信息的提取^[5]等诸多方面 ...

2022

0.0

... 由于高光谱成像技术的巨大优势, 成为遥感领域的一大热点, 正成为当代空间对地观测的主要技术手段^[6] ...

2023

0.0

... 由于受到传感器分辨率的限制以及成像地区地物分布复杂, 导致有大量混合像元存在于高光谱图像中^[7] ...

2024

0.0

... 混合像元的存在对地面信息的分析和解译造成困扰^[8], 所以需要对获得的高光谱图像进行解混, 以获得混合像元中纯净的物质和他们对应的比例 ...

2022

0.0

... 这些纯净物质被称为端元, 对应的比例被称为丰度^[9] ...

2015

0.0

... 现有的高光谱混合模型主要包括线性光谱混合模型和非线性光谱混合模型两种^[10], 由于非线性光谱混合模型参数多且难以求解, 通常用线性光谱混合模型近似^[11] ...

2017

0.0

2023

0.0

... 在线性解混中, 目前稀疏回归算法^[12]比较常用 ...

2023

0.0

... 它借助一个庞大的光谱库作为先验知识, 加之一些正则化条件, 估算出光谱库中端元对应的丰度系数, 实现对混合像元的解混^[13] ...

2011

0.0

... 目前比较经典且引用广泛的稀疏解混算法是由Iordache和Bioucas-Dias^[14]提出的基于分裂增广拉格朗日的稀疏解混算法(sparse unmixing via variable splitting and augmented Lagrangian, SUnSAL), 该方法为稀疏解混开辟了新的途径, 并带来了新的见解 ...

... 但由于使用l₀范数会导致求解时出现非凸优化NP(非确定性的多项式)困难问题, 于是Iordache和BioucasDias提出了SUnSAL算法^[14], 将l₀范数优化问题转化为凸优化l₁范数优化问题, 使得求解比较容易, 其模型如式(3) ...

2012

0.0

... 针对此问题, Iordache等^[15]把SUnSAL模型与全变差正则化项进行结合, 提出了基于分裂增广拉格朗日和全变差的稀疏解混算法(sparse unmixing via variable splitting augmented Lagrangian and total variation, SUnSAL-TV) ...

... 由于高光谱图像还包含丰富的空间信息, 于是Iordache等提出了SUnSAL-TV算法^[15], 在SUnSAL模型中增加了一个TV正则化项以利用图像的空间信息, 提高解混效果, 模型如式(4) ...

... 算法SunSAL-TV^[15]、 ADSpLRU^[18]、 SU-ATV^[17]、 S²WSU^[16]比较, 用以验证提出算法的性能优势 ...

... 1 模拟高光谱数据实验为了验证本文提出的基于自适应TV和低秩约束的高光谱图像稀疏解混方法(ATVLRSU)的有效性, 在模拟数据实验中, 我们把经典的SUnSAL-TV算法^[15], 具有空谱加权约束的S²WSU算法^[16], 具有低秩性的稀疏性解混算法ADSpLRU算法^[18]和具有自适应TV的稀疏解混算法SU-ATV算法^[17]与融合了稀疏、自适应TV和低秩功能的本文提出的ATVLRSU算法进行多方面的比较 ...

... 其生成过程可以参考文献[15] ...

2018

0.0

... Zhang等^[16]在SUnSAL模型基础上, 对丰度矩阵增加了空谱约束项, 提出了一种空谱加权的高光谱稀疏解混算法(spectral-spatial weighted sparse unmixing, S²WSU), 进一步提高了解混精度 ...

... 算法SunSAL-TV^[15]、 ADSpLRU^[18]、 SU-ATV^[17]、 S²WSU^[16]比较, 用以验证提出算法的性能优势 ...

2022

0.0

... 为此, 本团队对TV项进行改进, 提出基于自适应总变异化的稀疏解混算法(adaptive total variation regularized for hyperspectral sparse unmixing, SU-ATV)^[17] ...

... 本团队将自适应全变差(ATV)融合到高光谱解混中, 提出了自适应总变差解混模型(SU-ATV)^[17], 以更好地对解混结果去噪, 模型如式(5) ...

... 算法SunSAL-TV^[15]、 ADSpLRU^[18]、 SU-ATV^[17]、 S²WSU^[16]比较, 用以验证提出算法的性能优势 ...

...)假设定义阈值th=10且重构正确率p_s=1, 则意味着丰度估计的误差小于1/10, 文献[17]对于阈值的确定给出了说明: 当#cod#x02016 ...

2016

0.0

... 另外, 考虑到丰度矩阵中的向量高度相关, 使丰度矩阵表现出了低秩的特点, Giampouras等^[18]提出了同时具有稀疏性和低秩性丰度矩阵估计高光谱图像解混方法(alternating direction sparse and low-rank unmixing algorithm, ADSpLRU), 提高了解混算法的性能 ...

... 范数提出了同时具有稀疏性和低秩性丰度矩阵估计高光谱图像解混模型ADSpLRU^[18] ...

... 算法SunSAL-TV^[15]、 ADSpLRU^[18]、 SU-ATV^[17]、 S²WSU^[16]比较, 用以验证提出算法的性能优势 ...

2021

0.0

... 由于X表示为光谱库A对应的丰度系数, 是具有一定物理意义的对象丰度值, 其丰度系数应该满足丰度非负性^[19] ...

2019

0.0

... 此外, 由于光谱库A中包含的端元个数远大于高光谱图像中真实端元的个数, 所以X丰度矩阵表现出稀疏性^[20], 于是在模型中增加了稀疏约束项和非负约束 ...

2020

0.0

... 通常, 高光谱图像中的空间信息在不同区域拥有不同的结构^[21] ...

2020

0.0

... 由于丰度矩阵中的向量高度相关^[22], 使丰度矩阵表现出了低秩的特点, 一些方法通过引入低秩性进行约束, 以更好的地对丰度矩阵去相关, 使结果更加鲁棒 ...

2022

0.0

... 2 模型求解我们用交替方向乘子法(ADMM)^[23]来对模型进行求解, 过程如式(9) ...

2018

0.0

... 我们采用信号与重建误差比(signal reconstruction error, SRE)^[24]表示环境噪声进行定量分析, 其定义如式(20) ...

2018

0.0

...)是期望值, X^是丰度矩阵的估计值, 同时, 我们引入另一个评定指标丰度重构正确率^[25] ...

2021

0.0

2003

0.0

... 由于高光谱图像中包含的端元个数远大于高光谱图像中真实端元的个数, 所以丰度矩阵表现出稀疏性, 因此我们引入稀疏度^[27]作为第三个评定指标 ...

... 2 真实高光谱实验数据在本节中, 我们将使用广泛用于高光谱遥感图像分析的机载可见红外成像光谱仪(AVIRIS)于1995年采集的内华达州的Cuprite矿区数据^[27]作为真实高光谱进行比较和分析 ...

... 在去除了由不同干扰因素影响的波段后^[27], 仅留下188个光谱波段 ...

2021

0.0

... 该光谱库选自于具有权威性的美国地质勘探局(United States Geological Survey, USGS)端元光谱库^[28], 并在USGS端元光谱库中随机挑选240条光谱曲线作为模拟数据实验的光谱库 ...

2016

0.0

... Rn1×n2×p, p, n₁, n₂表示三个维度, 通常来说稀疏度越小, 则解混的结果越好^[29] ...

... 3软件^[29]制作的矿物分类图, 利用该软件产品来反映Cuprite矿区数据中各矿物的分布情况 ...