本文提出了一种基于物理规律主导因素并结合MLP的定量方法, 称为DF-MLP。 首先根据光谱物理知识, 单独使用光谱中与待测组分相关的特征谱线建立主导因素回归模型, 然后使用MLP学习主导因素模型的预测残差, 从而进一步修正主导因素的预测结果。

1.1.1 主导因素方法

样品待测组分主要元素的特征谱线强度与待测组分的浓度直接存在较高的相关性, 这是LIBS成分测量的主要理论依据。 因此, 可以利用这些特征谱线建立模型对待测变量进行较为初步的预测, 在主导因素方法中, 首先基于领域知识确定与元素浓度高度相关的对应特征谱线并建立线性模型, 这部分基于物理规律的预测结果称为主导因素, 可以获得待测变量的主要浓度信息。 然而由于基体效应、 信号不确定性等复杂因素的影响, 主导因素的定量精度往往不足, 因此, 我们进一步利用MLP基于全光谱信息建立非线性的残差修正模型估计这些因素的影响, 修正主导因素的预测残差, 提高了定量性能。 主导因素方法结合了光谱领域知识驱动的主导因素模型和数据驱动的基于机器学习方法的残差修正模型, 提高了模型的鲁棒性和定量结果的准确度。 另一方面, 由于残差修正模型在整个预测结果中的比例较小, 主导因素方法可以约束机器学习方法的过拟合风险, 从而提高了模型的泛化性能。

主导因素方法以图1所示流程训练。 首先根据光谱领域知识筛选出与待测组分相关的特征谱线作为主导因素, 建立预测待测组分浓度的主导因素模型。 主导因素模型训练完成后, 记录训练集上所有样本预测浓度的残差。 残差模型将全光谱作为输入, 输出为主导因素模型的预测残差。 主导因素方法预测未知样品待测元素浓度时, 主导因素模型直接预测待测组分浓度, 残差修正模型修正非线性因素导致的主导因素模型预测残差, 将两个模型的输出相加, 得到主导因素方法对样品待测组分的预测值。

图1

Fig.1

	Figure Option ViewDownloadNew Window
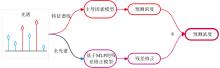	图1 主导因素方法示意图 红色谱线表示主导因素特征谱线, 蓝色谱线表示剩余谱线Fig.1 Schematic diagram of Dominant factor method The red lines represent characteristic lines of dominant factors and the blue lines represent the rest lines

理想条件下, 待测组分特征谱线与浓度呈线性关系, 所以主导因素一般采用线性模型, 如单变量线性回归、 多元线性回归(MLR)、 PLSR或使用线性核的SVR等。 而残差修正模型主要估计基体效应、 信号不确定性等复杂因素的影响, 一般采用较主导因素更为复杂的模型。 在我们以往的工作中, 已经证实PLSR、 SVR等方法建立残差修正模型的有效性^{[11, 12]}。 而多个研究表明MLP对高维非线性数据的拟合能力更强, 表现优于PLSR、 SVM、 K-ELM等方法^[14], 因此, 我们设计了主导因素多层感知机(DF-MLP)进一步提高主导因素方法的定量效果。

1.1.2 多层感知器残差修正

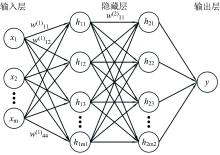
多层感知器(multilayer perceptron, MLP)是由输入层、 至少一个隐藏层和输出层组成的简单人工神经网络。 如图2所示, MLP每一层的所有神经元都与下一层的所有神经元直接连接, 下一层接收上一层的输出[式(1)]作为输入。 多层感知机通过后向传播算法[式(2)]和梯度下降算法[式(3)]迭代地调整网络参数, 降低模型的损失函数, 最终得到训练集上的拟合模型。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 MLP结构示意图Fig.2 Structure of MLP

i(n+1)=f(W(n)i(n)+b(n))(1)

∂L∂wij(n)=∂L∂wij(n+1)∂wij(n+1)∂wij(n)(2)

w^ij(n)=wij(n)-α∂L∂wij(n)(3)

其中, i⁽ⁿ⁾为第n层接收的输入, W⁽ⁿ⁾为第n层权重矩阵, b⁽ⁿ⁾为第n层偏置, L为损失函数, wij(n)表示第n-1层第i个神经元和第n层第j个神经元之间的权重, w^为每轮迭代更新后的权重, α 为学习率。

MLP是一种简单的神经网络, 在LIBS定量分析领域已有很多应用^{[7, 14, 15, 16]}。 MLP主要优势在于结构简单、 拟合能力强, 且不要求特征平移不变性, 更符合LIBS光谱特征。 但MLP的可解释性差, 容易过拟合, 模型可靠性弱。 本文提出的DF-MLP方法将MLP作为残差修正模型, 利用物理知识约束了MLP输出, 有效提高了模型的可靠性, 减弱了MLP过拟合对定量结果的影响。

1.2.1 样品及测量系统

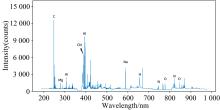
实验中使用的煤样来源于不同电厂, 总共包含339个样品, 由标准化验分析(GB/T 212— 214)测定了固定碳含量(%)、 灰分(%)和挥发分(%)。 煤样被研碎(粒径小于0.2 mm)并压饼(直径约30 mm, 压力分别为20吨和30吨)。 使用集成式LIBS系统(ChemReveal LIBS Desktop Elemental Analyzer 3766)测量光谱, 系统由波长为1 064 nm的Q开关Nd：YAG激光器和配有7个CCD探测器的7通道测量仪组成, 优化后的激光能量和光谱延迟时间分别为90 mJ/脉冲和0.5 μ s, 积分时间为1.05 ms固定不变。 聚焦直径为400 μ m。 测得光谱范围为186.87~979.23 nm, 光谱分辨率0.09 nm, 原始光谱包含12 990个变量。 每个样品在不同的位置共采集176个光谱并取平均值用于定量分析。 所有样品的平均光谱如图3所示, 其中固定碳、 灰分、 挥发分含量分析中, 信号较强的特征谱线包括C Ⅰ (247.877 nm)、 CN(387.039 nm)、 CN(388.259 nm), H Ⅰ (656.274 nm)等^[17]。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 实验煤样平均原始光谱示意图Fig.3 Average raw spectrum of samples for coal analysis

1.2.2 基线方法

本文用于对照的基线方法包括单变量回归、 多元线性回归(MLR)、 PLSR、 SVR及常规MLP。 MLR是传统知识驱动模型常用定量方法, 在多个自变量和单个因变量之间建立线性关系。 PLSR利用自变量的线性组合提取主成分, 能有效解决高维、 共线性问题。 SVR使用核方法将数据映射到高维特征空间, 搜索最优回归超平面。 PLSR和SVR是LIBS定量分析中常用的线性和非线性模型。

实验中使用测试集上的平均绝对误差(MAEp)和均方根误差(RMSEp)作为评估模型性能的标准, MAE_p和RMSE_p越低, 模型对未知样品的预测准确度越高, 定量性能越好。

1.2.3 特征谱线的选择和模型优化

原始光谱经谱峰搜索、 基线去除和峰面积计算的预处理后, 变量数为500。 将特征谱线按照光谱面积排序, 依次添加为主导因素, 根据先验知识和交叉验证结果, 选择了12条与煤质分析相关程度较高的特征谱线作为主导因素变量, 如表1所示, 这里值得说明的是, 使用C、 H相关谱线作为主导因素作为灰分预测的原因是认为这些谱线和灰分之前存在负相关的关系, 即较少的C/H元素意味着更多的灰分。

表1

Table 1

表1(Table 1)

表1 主导因素特征谱线 Table 1 Characteristic lines of dominant factors 元素 波长/nm C 247.877 CN 385.408、 386.143、 387.039、 388.259 C2 468.394、 469.603、 471.427、 473.622、 512.839、 516.439 H 656.274

表1 主导因素特征谱线 Table 1 Characteristic lines of dominant factors

将数据集按照7：3的比例随机划分为训练集和测试集。 各个模型在固定碳、 灰分、 挥发分三个任务上分别优化。 其中, PLSR和SVR根据训练集上的5折交叉验证结果确定, 人工神经网络(artificial neusal network, ANN)的超参数根据训练集进一步随机划分的验证集上的结果确定。 在本文中MLP模型使用Sigmoid函数作为激活函数。

首先对比了主导因素对单变量方法的效果, 根据交叉验证结果, 从表1的12条特征谱线中分别选取固定碳、 挥发分和灰分的一条谱线作为变量, 分别建立单变量模型和单变量主导因素模型。 结果如图4所示, 单变量主导因素模型的效果明显优于单变量模型, 证明了主导因素方法对定量模型的修正作用, 残差修正模型可以改善基体效应等复杂因素导致的预测误差, 从而提高模型的定量效果。

图4

Fig.4

	Figure Option ViewDownloadNew Window
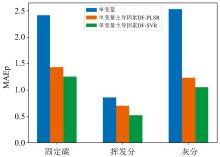	图4 单变量模型与单变量主导因素模型性能对比Fig.4 Comparison between single variable models and single variable dominant factor models

我们进一步比较了多变量模型与多变量主导因素模型的性能。 根据交叉验证结果选择了12条特征谱线用于建立主导因素模型, 并分别选择了不同任务残差修正模型参数或网络结构, 其中SVR主导因素模型对应的残差修正网络结构如表2所示。

表2

Table 2

表2(Table 2)

表2 MLP残差修正模型网络结构 Table 2 Network structure of MLP residual correction models 任务 隐藏层数 结点数量 固定碳 2 256、 8 灰分 2 256、 8 挥发分 2 128、 4

表2 MLP残差修正模型网络结构 Table 2 Network structure of MLP residual correction models

展示了各基线方法和对应不同的残差修正主导因素方法的性能。 对于SVR主导因素模型, 为了保持光谱领域知识中的线性关系, 选用线性核函数建立特征谱线和待测组分浓度的映射关系。 此外, 主导因素模型选用线性核SVR时对光谱进行了归一化处理。 与基线方法对比, 使用线性核SVR主导因素模型的PLSR、 SVR和MLP残差修正方法定量精度均有一定幅度的性能提升, 其中使用线性核SVR的DF-MLP模型性能最优, 性能提升幅度最大, 固定碳、 灰分和挥发分任务的RMSE_p分别降低了13.21%、 14.54%和21.77%。 线性SVR的DF-MLP在测试集上的预测结果如图5所示。

表3

Table 3

表3(Table 3)

表3 主导因素方法性能对比 Table 3 Model performance comparison of different dominant factor methods 主导因素模型 修正模型 固定碳/% 灰分/% 挥发分/% MAEp RMSEp MAEp RMSEp MAEp RMSEp MLR - 1.677 2.128 1.016 1.442 1.350 1.876 DF-PLSR 1.472 2.173 0.976 1.391 1.114 1.571 DF-SVR 2.045 3.144 0.904 1.393 1.195 1.650 DF-MLP 1.224 1.934 0.977 1.392 0.967 1.523 PLSR - 1.369 1.964 0.694 1.015 1.168 1.625 DF-PLSR 1.504 1.984 0.976 1.331 1.115 1.559 DF-SVR 1.934 2.825 0.953 1.409 1.200 1.646 DF-MLP 1.168 1.695 0.552 0.962 1.011 1.650 线性核SVR - 1.176 1.787 0.583 1.060 1.187 1.540 DF-PLSR 1.278 1.802 0.682 1.003 1.008 1.414 DF-SVR 1.080 1.641 0.580 1.055 0.976 1.418 DF-MLP 0.960 1.399 0.485 0.811 0.856 1.333 MLP - 1.099 1.612 0.484 0.949 1.099 1.704

表3 主导因素方法性能对比 Table 3 Model performance comparison of different dominant factor methods

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 线性SVR的DF-MLP模型对测试集样品的预测结果Fig.5 The linear SVR based DF-MLP's prediction of test set samples

进行进一步分析, 不使用残差修正的MLP方法相比于主导因素MLR和主导因素PLSR反而有更好的表现。 同时, 仅当主导因素模型使用线性核SVR时, 主导因素方法可以全面提升定量性能, 而MLR或PLSR主导因素模型仅在MLP残差修正模型上性能得到了提升。 这是因为主导因素方法中, 主导因素模型直接预测待测组分浓度, 对模型的贡献远大于残差修正模型, 残差修正模型的输出仅占模型预测结果的2%~10%, 因此在主导因素模型表现较差时, 简单的残差修正模型无法校正偏差, 并造成更大偏差。 因此, 主导因素模型性能越好、 对待测组分浓度预测越精确, 主导因素方法的效果越好。 主导因素模型预测精度低下导致残差修正模型建模更加困难, 修正效果差, 因此令主导因素方法失效。

与基线方法相比, 主导因素方法并没有引入更多的光谱变量, 但根据物理规律将线性成分和非线性成分分开建模的方式改善了定量结果。 实验结果证明了主导因素方法是提升LIBS定量分析能力的可行方法, 与人工神经网络结合可进一步提高预测精度。 与非主导因素方法相比, 主导因素方法并不是通过提取特征谱线实现光谱知识的引入, 而是通过将特征谱线对浓度预测的影响分离出来, 使其在模型中起主导作用实现的, 因此主导因素方法效果优于简单使用特征提取或全光谱的建模方式。 但不理想的主导因素模型会造成主导因素方法的失效, 因此提高模型性能的关键在于优化主导因素模型。

在现有主导因素方法的工作中, 残差修正模型有两种不同形式: 使用全光谱建模^[13]或剔除主导因素后使用剩余光谱(非主导因素)建模^{[11, 12]}。 前文展示的结果均使用全光谱建模, 表4展示了非主导因素残差修正模型的效果。 其中, 主导因素模型均为线性核SVR。 DF-MLP中, 由于两种方式中残差修正模型的输入维度变化较小(500和488), 非主导因素残差修正模型采用了相同的MLP网络结构。 而DF-MLP^* 单独对非主导因素残差修正模型调参, 结果如表5所示。

表4

Table 4

表4(Table 4)

表4 非主导因素残差修正模型(使用剩余光谱建立的残差修正模型)性能 Table 4 Model performance of residual correction model (residual correction modelling using residual spectra) establishing with non-dominant factors 方法 固定碳/% 灰分/% 挥发分/% MAEp RMSEp MAEp RMSEp MAEp RMSEp DF-PLSR 1.268 1.796 0.681 0.997 1.012 1.427 DF-SVR 1.087 1.724 0.543 1.083 0.964 1.317 DF-MLP 1.203 1.865 0.546 0.958 1.089 1.521 DF-MLP* 0.981 1.675 0.464 0.762 0.906 1.327

表4 非主导因素残差修正模型(使用剩余光谱建立的残差修正模型)性能 Table 4 Model performance of residual correction model (residual correction modelling using residual spectra) establishing with non-dominant factors

表5

Table 5

表5(Table 5)

表5 DF-MLP* 残差修正模型网络结构 Table 5 Network structure of DF-MLP* residual correction models 任务 隐藏层数 结点数量 固定碳 2 128、 16 灰分 2 64、 16 挥发分 2 64、 4

表5 DF-MLP* 残差修正模型网络结构 Table 5 Network structure of DF-MLP* residual correction models

实验结果显示, 残差修正模型是否包含主导因素对DF-PLSR和DF-SVR影响较小, 而对DF-MLP影响显著。 对DF-MLP的进一步调参结果显示 MLP的网络结构产生了变化, 这意味着MLP残差修正模型在有无主导因素的前提下采用了不同的计算结构。 重新调参后的DF-MLP^* 与全光谱DF-MLP相比, 灰分含量预测精度小幅度提高, 固定碳和挥发分含量预测精度略微下降。 考虑到主导因素模型的预测残差来源复杂, 如基体效应、 信号不确定性和模型本身的偏差等, 其中部分因素不仅影响非特征谱线, 同样对特征谱线强度有一定的干扰, 因此添加主导因素有利于残差修正模型估计主导因素模型的残差。 因此推荐在使用DF-MLP时使用全光谱残差修正模型。