引用本文
冀哲, 李正强, 马, 姚前, 张鹏, 陈震霆. 地表方向反射特性对AOD反演误差的影响研究[J]. 光谱学与光谱分析, 2025,45(3): 852-862.
JI Zhe, LI Zheng-qiang, MA Yan, YAO Qian, ZHANG Peng, CHEN Zhen-ting. Study on the Influence of Surface Non-Lambertian Reflection Characteristics on AOD Retrieval Error[J]. Spectroscopy and Spectral Analysis, 2025,45(3): 852-862.
Doi:10.3964/j.issn.1000-0593(2025)03-0852-11  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
地表方向反射特性对AOD反演误差的影响研究
冀哲1,2,3, 李正强1,2,4, 马1,2,*, 姚前1,2,3, 张鹏1,2,3, 陈震霆5
1. 中国科学院空天信息创新研究院国家环境保护卫星遥感重点实验室, 北京 100101
2. 中国科学院空天信息创新研究院遥感与数字地球重点实验室(中国科学院), 北京 100101
3. 中国科学院大学, 北京 100049
4. 空天信息大学(筹), 山东 济南 250200
5. 昆明学院信息技术学院, 云南 昆明 650214
*通讯作者 e-mail: mayan01@aircas.ac.cn

作者简介: 冀 哲, 2000年生, 中国科学院空天信息创新研究院博士研究生 e-mail: jizhe221@mails.ucas.ac.cn

收稿日期: 2024-04-29 修回日期: 2024-08-06
基金: 国家杰出青年科学基金项目(41925019), 对外技术合作科研项目(E3KZ03010F), 国际大气环境遥感科研开放平台建设(E2D1030200), 云南省李正强专家工作站(202205AF150031)资助
摘要

分离地表贡献是反演气溶胶光学厚度(AOD)的关键步骤。 传统针对单角度载荷开发的反演算法通常假设地表为均一朗伯体, 忽略了地表的各向异性, 从而带来了误差。 然而, 由于信息量不足考虑地表特性会产生病态反演问题, 因此需要引入先验知识刻画地表各向异性参数。 通常使用一定时间范围内均值作为地表参数的先验值, 但地表情况随时间变化, 使用平均值会造成地表贡献估计的不准确。 为了评估使用平均值对反演精度的影响, 该研究基于2022年的MODIS双向反射分布函数产品(MCD43C2)进行了分析, 并结合MODIS地表分类产品(MCD12C1), 对全球不同地表覆盖类型的各向同性散射核系数进行统计。 结果显示, 该参数在以林地为主要覆盖的场景下一般低于0.05, 在草地、 耕地以及城镇为主要覆盖的场景下有近90%的情况低于0.1。 根据统计的经验值, 模拟了不同地表类型下表观反射率可能出现的误差, 并基于模拟结果反演AOD; 经与预设的AOD“真值”对比发现, 相对于植被覆盖较少的亮地表, 在植被覆盖较高的地表处, 以季度平均值作为该位置处的双向反射分布函数(BRDF)形状参数产生误差较少。 即当太阳高度角为50°, AOD真值为0.4时, 常绿阔叶林区域的平均反演绝对误差最大为0.053; 近90%的草地、 耕地以及城镇区域平均反演绝对误差最大分别为0.089/0.083/0.113。 但在亮地表区域, AOD平均反演绝对误差显著增加, 最大值达到0.145。 这表明使用季度平均BRDF形状参数作为AOD反演中的地表约束的可靠性随着地表反射率的升高而降低, 即使用地表信号占主导的标量卫星观测进行气溶胶的反演, 存在不可避免的不确定性。 因此, 使用多角度偏振观测实现BRDF和AOD的协同反演是未来提高气溶胶反演精度的重要方向。 研究结果可以对全球不同地表类型区域的BRDF核系数分布提供先验知识, 且进一步探究了基于非朗伯前向辐射传输模型反演AOD的误差来源, 并给定了可能的误差区间。

关键词: 气溶胶光学厚度; 双向反射分布函数; 辐射传输模型; MODIS
中图分类号:TP79 文献标志码:A
Study on the Influence of Surface Non-Lambertian Reflection Characteristics on AOD Retrieval Error
JI Zhe1,2,3, LI Zheng-qiang1,2,4, MA Yan1,2,*, YAO Qian1,2,3, ZHANG Peng1,2,3, CHEN Zhen-ting5
1. State Environmental Protection Key Laboratory of Satellite Remote Sensing, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China
2. Key Laboratory of Remote Sensing and Digital Earth, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China
3. University of Chinese Academy of Sciences, Beijing 100049, China
4. Aerospace Information Technology University, Jinan 250200, China
5. School of Information Engineering, Kunming University, Kunming 650214, China
*Corresponding author
Abstract

Separating the surface contribution is crucial in aerosol optical depth (AOD) inversion. Traditional retrieval algorithms developed for single-angle sensors typically assume that the surface is homogeneous Lambertian, which ignores surface anisotropy and introduces errors. However, considering surface properties can create an ill-posed inversion, so it is necessary to introduce a priori knowledge to characterize the surface anisotropy parameters. Using the mean value over a certain time range as a fixed value for the surface parameter is a common practice. However, surface conditions vary over time, and averaging can lead to inaccuracies in estimating the surface contribution. This paper analyzes the anisotropic scattering kernel coefficients of various surface cover types to evaluate the effect of the mean value on inversion. The analysis is based on the MODIS bidirectional reflectance distribution function product (MCD43C2) for 2022 and the MODIS surface classification product (MCD12Q1). The statistical analysis indicates that when forested land is the dominant cover, the parameter is generally lower than 0.05. In nearly 90% of the cases where grassland, cropland, and towns are the dominant covers, the parameter is lower than 0.1. This paper presents a simulation of the potential errors in apparent reflectance under diverse surface types, intending to invert the AOD based on the simulation findings. A comparison of the results with the preset “true value” of the AOD revealed that the quarterly mean value of the BRDF shape parameter was less prone to producing errors in the location of the quarterly mean value of the BRDF shape parameter than the bright surfaces with less vegetation cover and the more highly covered surfaces. The shape parameter of the bi-directional reflectance distribution function (BRDF) at this location produces fewer errors than brighter surfaces with less vegetation cover. In other words, at a solar zenith angle of 50° and a true value of AOD of 0.4, the mean absolute error of retrievals is 0.053 for evergreen broadleaf forests and 0.089/0.083/0.113 for nearly 90% grasslands, croplands, and towns, respectively. However, the mean absolute error of retrievals of AOD is significantly higher in the bright surface area, reaching a maximum value of 0.145. This is the case for nearly 90% of the grassland, cropland, and urban regions. However, the mean absolute error of retrievals is only 0.078/0.107 for the remaining areas. This indicates that using quarterly-averaged BRDF as a surface constraint in AOD retrievals becomes less reliable with increasing surface reflectivity. This is due to the inherent uncertainty in using scalar satellite observations, where the surface signal dominates. Consequently, the synergistic inversion of BRDF and AOD using multi-angle polarization observations represents a promising avenue for enhancing the accuracy of aerosol inversion in the future. The findings of this study offer insights into the distribution of BRDF kernel coefficients across different surface types globally. Additionally, this research delves into the sources of errors in AOD inversion based on the non-Lambertian forward radiative transfer model. The study also presents the potential error ranges associated with this process.

Keyword: Aerosol optical depth; Bidirectional reflectance distribution function; Radiative transfer model; MODIS
0 引言

大气气溶胶是由悬浮在大气流体由中不同形态和组分的液滴或颗粒物构成的[1], 其复杂的物理化学特性, 会导致潜在的气候变化[2], 包括但不限于直接或间接的影响全球辐射强迫[3], 影响云地辐射特性[4], 并降低空气质量甚至威胁到人类健康[5, 6]。

气溶胶光学厚度(AOD)作为评估气溶胶特性的重要参数, 对其的定量反演已有长时间的研究, 由于陆地地表的复杂性, 陆地上空的气溶胶反演一直以来是卫星遥感气溶胶特性的主要方向[7, 8, 9, 10, 11]。 其中, 大部分的反演算法简化了地表的描述, 即不考虑地表的方向反射特性, 认为地表是均一的朗伯体, 但实际情况中忽略地表的各向异性在特定情况下可能会造成较大误差[12]。

为了考虑地表方向反射特性对表观反射率的影响, Vermote等提出了复杂的非朗伯前向模型, 经验证其具有极高的模拟精度[13], 但它涉及到积分运算, 并耦合了大气与地表的贡献, 因此难以应用于查找表反演算法。 Qin等改进了原有的四通量非朗伯前向模型, 使其在具有完备物理意义的前提下, 获得了更高的精度, 并且该模型不涉及复杂的积分运算, 可直接应用于构建查找表, 因此, 本研究选择后者进行前向辐射传输模拟。 目前已有研究将非朗伯前向模拟应用于卫星气溶胶反演并取得了较好的结果[11, 12, 14, 15]。

非朗伯辐射传输模拟的计算涉及到地表双向反射分布函数(BRDF)的应用, Schaaf等利用MODIS传感器经过多年研究得到了高精度的BRDF反演结果。 已有研究表明, MODIS的BRDF模型— — Ross-Thick Li-Sparse (RTLS)可以准确的描述地表方向反射特性[16], 该模型可分为取决于地表微物理特性的地表各向同性散射核系数, 以及与地表结构相关的BRDF形状参数。 地表结构一般较为稳定, BRDF形状参数被认为在不同年份的同一时期变化较小[17], 本工作选用NASA的地表BRDF/Albedo官方产品— — MCD43C2进行表观反射率的模拟。

单角度观测模式的传感器在反演物理参量时由于信息量较少, 反演通常是病态的, 即单一像元无法在反演AOD的同时反演地表参数, 因此在考虑复杂地表特性的同时, 为了反演AOD需要对地表进行假设并引入先验知识。 目前已有大量的研究基于BRDF形状参数的光谱相似性进行地表各向异性与气溶胶参数的联合反演。 Yang基于MODIS DT算法代码, 使用非朗伯辐射传输模型得到了精度更高的气溶胶参数反演结果[12]。 Lyapustin利用两颗MODIS多天、 多角度的观测, 并基于蓝光波段(0.47 μ m)与短波红外波段(2.1 μ m)地表BRDF形状参数相似的假设, 实现了高精度的气溶胶参数反演[10, 11]。 Thomas和Shi也利用MODIS的BRDF产品, 同样基于BRDF形状参数的光谱相似性实现了基于AATSR数据的气溶胶反演算法开发[20, 21]。 通常, 研究者会使用一定时间范围内BRDF模型参数的平均值, 但地表结构在该时间范围内并非定值, 仍会随着时间变化, 使用平均值可能会对AOD反演带来一定的误差。 针对这一问题本工作评估了使用季均BRDF模型参数作为地表约束可能会对AOD反演造成的误差, 并对不同条件下该误差的分布情况进行了统计。

1 数据源
1.1 MODIS-BRDF产品

MODIS基于16天的观测数据得到了高精度的BRDF反演产品, 并在反演过程中假设地表特性在该时间范围内保持不变。 但不足的是, 由于其严格的条件限制, 单一产品在部分地区缺少高精度的反演结果。 因此, 为了满足在上述缺失地区反演AOD的需求, 使用季度平均结果作为地表BRDF的先验值以实现对上述地区缺失值的填充。

本研究收集了2022年期间的MCD43C2数据产品, 其空间分辨率为0.05° , 包含了 MODIS可见光到短波红外共7个波段的BRDF核系数数据, 质量控制标识(QA)以及误差等参数。 需要注意的是, 气溶胶参数反演一般使用对气溶胶颗粒更为敏感的蓝光波段, 因此仅展示MODIS-466 nm波段的BRDF。 为了减少BRDF产品质量较差对反演结果的影响, 在求取时间平均结果时, 仅选取反演质量最高, 即QA等于0的数据进行统计。

1.2 MODIS地表分类产品

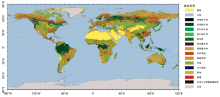
不同地表覆盖类型由于其植被覆盖的比例与种类不同, BRDF特性具有较大差异, 因此需要考虑不同地表覆盖类型下BRDF对AOD反演的影响。 为了匹配MCD43C2产品的空间分辨率与时间范围, 本研究同样使用2022年MODIS的地表分类产品MCD12C1, 其具有与MCD43C2相同的空间分辨率, 时间分辨率则为1年。 最终从MCD12C1提供的多种分类方案结果中选择使用IGBP分类结果, 其将全球土地覆盖划分为植被、 城镇和水体等共17种类别, 如图1所示。

图1 2022年全球MCD12C1-IGBP地表类型图Fig.1 Global MCD12C1-IGBP land surface type map in 2022

2 研究方法
2.1 BRDF形状

MODIS使用Ross-Thick Li-Sparse(RTLS)模型作为其地表BRDF/Albedo官方产品的反演模型[16]。 RTLS模型考虑了地表各向同性散射(isotropic)、 基于水平均一假设的叶片冠层的体散射(volumetric)以及目标三维场景的几何光学散射(geometric-optical), RTLS模型表达式如式(1)

ρsur(λ, θs, θv, φ)=fiso(λ)Kiso(θs, θv, φ)+fvol(λ)Kvol(θs, θv, φ)+fgeo(λ)Kgeo(θs, θv, φ)(1)

式(1)中, ρsurλ, θs, θv, φ为地表二项性反射分布函数, Kisoθs, θv, φ、Kvolθs, θv, φ以及 Kgeoθs, θv, φ分别代表各向同性散射核、体散射核以及几何光学散射核, fisoλ、fvolλ以及 fgeo(λ)分别为对应的核系数。

Bré on等将体散射核以及几何光学核进行归一化得到BRDF形状参数, 并假设其随NDVI线性变化以反演BRDF核系数, 基于大量对BRDF/Albedo特性的相关研究, BRDF形状已被广泛应用于地表参数估计及大气校正中[15, 18]。 因此, RTLS模型可改写如式(2)

ρsur(λ, θs, θv, φ)=fiso(λ)[Kiso(θs, θv, φ)+fvol(λ)fios(λ)Kvol(θs, θv, φ)+fgeo(λ)fiso(λ)Kgeo(θs, θv, φ)]F(λ, θs, θv, φ)=[Kiso(θs, θv, φ)+fvol(λ)fios(λ)Kvol(θs, θv, φ)+fgeo(λ)fiso(λ)Kgeo(θs, θv, φ)](2)

式(2)中, Fλ, θs, θv, φ为BRDF形状, 记 p1=fisoλ, a2=fvolλfisoλ, a3=fgeoλfisoλ。其中, a2与植被数量和类型相关, a3则与地表粗糙度的变化相关。 可以预见, 植被覆盖随时间的变化远大于地表粗糙度的变化, 因此a2相对于a3对时间的变化更加敏感, 但不同年份同一时期, 同一位置的地表结构与植被覆盖变化较小因此一般可以认为BRDF形状参数在不同年份的同一时期的变化是可忽略的[19]。

2.2 非朗伯前向辐射传输模型

对于水平均一大气的无云地气系统, 模拟表观反射率时常假设地表朗伯均一。 但现实情况中, 地表通常是非朗伯体, 具有方向辐射特性。 为了考虑大气下行辐射与地表BRDF的相互作用, Qin等在原有四通量辐射传输模型的基础上得到了改进后的非朗伯前向辐射传输模型[15], 在不考虑气体吸收的情况下, 如式(3)所示

ρTOA=ρ0+T→(μs)TR→T→(μv)-e-τ/μs|R→|e-τ/μv1-ρBHRS(3)

式(3)中, R→为反射率矩阵, ρ BHR为半球-半球反照率, 上行透过率矩阵 T→μs=e-τμs　tdμs, 下行透过率矩阵 T→μv=e-τμv　tdμv, ρ0为大气程辐射, τ为大气光学厚度, S为半球反照率, μs与 μv分别为太阳天顶角与观测天顶角的余弦。

R→=ρρDHRρHDRρBHR(4)

式(4)中, ρ DHR为方向-半球反照率, ρ HDR为半球-方向反照率。 由于其无需涉及复杂的积分运算, 并具有较高的精度, 目前该式已被证明可用于AOD的反演[12]。 因此选用该模型进行辐射传输模拟。

2.3 使用季均BRDF形状参数对AOD反演的误差分析

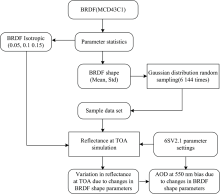
MODIS的BRDF产品在反演时并未假设体散射核系数或几何光学核系数与p1成线性关系, 因此使用季均的BRDF形状参数作为这一时间范围内的恒定值可能会带来较大的误差。 为了评估季均值与实际值的差异对AOD反演的影响, 统计了全球2022年MCD43C2产品的季均结果与相应时间范围内BRDF形状参数的标准差。 最终通过使用服从上述均值与标准差的高斯分布概率函数进行采样, 得到了满足上述概率分布的测试样本, 该样本同时考虑了a2与a3变化对表观反射率的影响。

其中, 假设大气服从高精度矢量辐射传输模型6SV2.1中内置的中纬度夏季模式, 气溶胶模型假设为大陆型, 定义海拔高度为1 m, 即以近似标准大气压条件计算瑞利散射, 并不考虑气体吸收带来的影响, 其余参数的详细设置见表1。

表1 6SV2.1参数设置 Table 1 6SV2.1 parameter setting

AOD反演一般采用查找表插值方法, 即通过对比模拟与观测的表观反射率, 找到使二者差异最小的AOD, 因此模拟的误差会传递至反演结果。 为了量化这一误差, 我们进行了AOD的仿真反演, 其中查找表的计算由6SV2.1辐射传输模型实现, 参数设置见表1。 需要注意的是, 本工作通过假设MCD43C2-BRDF产品即为真实地表情况, 并不考虑BRDF产品自身的反演误差对AOD反演带来的影响。 反演时, 我们假设使用季均BRDF形状参数计算得到的表观反射率为观测值, 而基于BRDF形状参数样本数据集计算得到的不同AOD条件下的表观反射率为模拟值, AOD反演误差评估的流程如图2所示。

图2 AOD反演误差分析流程图Fig.2 AOD inversion error analysis flow chart

3 结果与讨论
3.1 RTLS模型系数季度统计结果

统计发现, MCD43C2在月均尺度上满足最高精度反演要求的结果较少, 将其直接应用于AOD反演时较低的覆盖度将限制反演的场景, 使用年均结果虽降低了该影响, 但地表特性随时间的变化, 会对反演带来较大的误差[14]。 综上, 最终选择季度平均作为地表约束以获得最大的收益, 并统计了单个像元在季度范围内的均值与标准差, 最终按照不同的地表覆盖类型对结果进行平均。 需要注意的是, 仅对12种IGBP地表分类情况进行统计, 这是由于部分地表覆盖条件下高质量BRDF参数反演结果较少, 不具备统计特征。

在MCD43C2产品中提供了7个波段的BRDF核系数反演结果, 但AOD反演一般使用对大气信息较为敏感的蓝光波段, 因此仅对466 nm波段进行统计分析。

全球BRDF核系数季度统计结果如图3所示, 由于云、 雪的影响, 高纬度处的MCD43C2产品在DJF与SON存在大量空缺值, 而南美洲北部、 非洲中部以及印度北部由于频繁的生物质燃烧或工业污染导致气溶胶浓度长期处于高值, 同样缺少高精度的BRDF反演结果。 与预期相同, p1在裸地表现出高值, 在植被覆盖地区表现出低值。 BRDF形状参数恰与其相反, p1在裸地表现出低值, 而在植被覆盖地区表现出高值[17]。 如图4显示, 在高纬度地区, BRDF形状参数随时间变化的幅度存在差异, 但这也可能是由于MCD43C2产品自身的误差造成的, 鉴于其较大的变化幅度, 不建议在该地区使用季均值作为定值进行AOD反演。

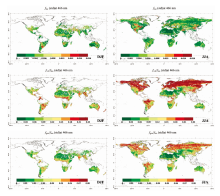图3 RTLS-BRDF核系数季度平均全球分布图Fig.3 Global distribution map of quarterly average of RTLS-BRDF kernel coefficient

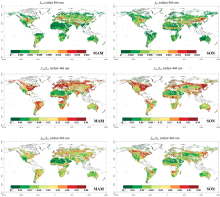图4 RTLS-BRDF核系数季度标准差全球分布图Fig.4 Global distribution map of quarterly standard deviation of RTLS-BRDF kernel coefficients

为了定量描述不同地类覆盖条件下BRDF形状系数在季度时间尺度上的变化, 通过计算标准差与平均值的比值, 并将其称为“ 变化系数” (VAR)来衡量BRDF随时间的变化。

由表2可知, p1较稳定, 除裸地外, 其他结果均小于0.1, 且随着季节的变化, 并未出现较大的波动。 鉴于绝大部分地表类型的p1较小, 因此变化系数更能表征该参数在时间范围内的变化, 落叶阔叶林在除JJA外所有时间范围内均表现出最大的变化, 耕地次之, 这可能是由于上述地表类型更易受时间的影响。 例如, 在农作物未生长的DJF, p1的变化系数很小, 而在作物生长的MAM、 JJA以及收获的SON, p1的变化系数显著增高。

表2 fiso季均统计结果(466 nm) Table 2 fiso quarterly average statistical results (466 nm)

由表3和表4可知, 与Bré on等[18]的结论相似, a2的季均值在植被覆盖较高的地区明显高于裸地, 且在MAM差异达到最大。 除常绿阔叶林, 裸地以及郁闭灌木林外, 其他地表类型在不同季节间均表现出较大的变化, 这可能是由于植被生长随时间变化而导致的结果。 需要注意的是, 与其他植被覆盖类型不同, 在所有季节内a2的季均最低值均出现在郁闭灌木林, 可能是由于郁闭度高导致冠层下散射光较弱。 a3的季均值统计结果与a2完全相反, 虽然裸地区域的季均值仍低于其余各类, 但在植被覆盖较高地区的变化系数明显低于裸地, 最大差异同样出现在MAM。 另一方面, a3在不同季节间未表现出较大的变化, 由于其与地表粗糙度或地表起伏程度相关, 而地表一般不随季节发生剧烈变化, 因此这一现象的出现是可以预料的。

表3 fvol/fiso季均统计结果(466 nm) Table 3 fvol/fiso quarterly average statistical results (466 nm)
表4 fgeo/fiso季均统计结果(466 nm) Table 4 fgeo/fiso quarterly average statistical results (466 nm)

为了进一步讨论BRDF形状参数的影响, 我们需要确定不同地表覆盖条件下各向同性散射核的取值范围。

为了减少相似地表分类造成的重复, 将常绿针叶林, 常绿阔叶林, 落叶阔叶林与混交林划分为林地类, 而将郁闭灌木林, 稀疏灌丛, 有林草地, 稀树草原以及草地划分为草地类。 统计结果如图5所示, 可以很明显的观察到林地类的p1均低于0.05, 草地类、 耕地以及城镇的p1低于0.1的比例分别为85%, 91%和88%(DJF); 81%, 92%和89%(MAM); 88%, 93%和88%(JJA); 84%, 91%和86%(SON), 裸地的p1均高于0.05。 最终选择0.05, 0.1和0.15作为p1的预设值来表征不同地表类型的情况。

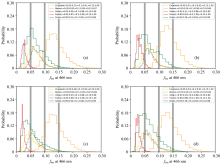图5 p1在不同地表类型以及不同季度范围内的概率分布统计
DJF代表12月— 1月— 2月; MAM代表3月— 4月— 5月; JJA代表6月— 7月— 8月; SON代表9月— 10月— 11月Fig.5 Probability statistics plot of p1 in different land surface types and different seasonal ranges
DJF stands for December— January— February; MAM stands for March— April— May; JJA stands for June— July— August, and SON stands for September— October— November

3.2 使用季均BRDF形状参数对模拟表观反射率的影响

通过使用服从表2内各个地表覆盖类型平均值与标准差的高斯概率分布对两个BRDF形状参数进行随机抽样, 共抽样了6 144次以构建测试数据集。 因为本工作仅针对BRDF形状参数对表观反射率的影响进行分析, 按照上一节的结果, 将p1设置为0.05、 0.1和0.15, 大气参数与观测几何设置见表1。 最终根据给定的地表与大气参数, 按照式(3)模拟表观反射率。

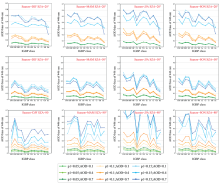
将不同情况计算得到的表观反射率与使用季均值得到结果差的最大值作为由BRDF形状参数变化引起的误差, 如图6所示。 当p1不变时, 误差随着AOD的升高而降低, 因此在低AOD场景反演的难度要大于高AOD场景。 另外我们可以发现郁闭灌木林与稀疏灌木林(除JJA)相较于其他地表类型(除裸地)在所有季度内均得到最小的表观反射率模拟误差。 这表明郁闭灌木林与稀疏灌木林相较于其他地表类型(除裸地)季均值更符合实际情况。 另一方面我们发现虽然随着季节的变化, 各个地表类型间表观反射率模拟误差的绝对量级没有发生较大变化, 但不同地表类型间表观反射率模拟误差的差异存在着较大的变化, 从而导致了由各地表类型误差构成的线性形状的改变。 因此, 我们初步认为在不同季节使用季均值的可靠性随时间变化, 这一现象的产生可能是由各地表类型的特性所决定, 对于更详细的分析, 我们将在后续的研究中展开。

图6 以季度时间范围内使用不同的IGBP地表分类的BRDF形状参数平均统计结果在不同太阳高度角条件以及不同AOD条件下模拟的466 nm处表观反射率的误差图
ENF: 常绿针叶林; EBF: 常绿阔叶林, DBF: 落叶阔叶林; MF: 混交林; CS: 郁闭灌木林; OS: 稀疏灌木林; WS: 有林草原; Sa: 稀树草原; Gr: 草原; Cr: 农田; UB: 城镇; Ba: 裸地Fig.6 The error plot of simulated apparent reflectance at 466nm with different IGBP classifications in the quarterly time range under different solar zenith angles and different AOD values
ENF: Evergreen needleleafforest; EBF: Evergreen broadleaf forest; DBF: Deciduous broadleaf forest; MF: Mixed forest; CS: Closed shrubland; OS: Open shrublands; WS: Woody savannas; Sa: Savanna; Gr: Grassland; Cr: Farmland; UB: Town; Ba: Barren

3.3 使用季均BRDF形状参数对AOD反演的影响

由于篇幅限制, 依据各地表类型的概率分布结果, 最终选择了植被稀疏的裸地, 地表结构复杂的城市、 以高大稀疏的树木为主的常绿阔叶林和以低矮密集的树丛为主的草地进行模拟。

为了进一步量化AOD反演误差, 对不同地表类型在各季节内的反演误差进行了统计(表5), 分别计算了不同VZA条件下反演误差的最大值, 平均值与最小值。 根据统计结果的分布情况, 对于p1结果较少地表类型, 将其相应结果标记为空值, 记为“ -” 。

表5 AOD反演误差统计结果(SZA=50° ) Table 5 AOD retrievals error statistics (SZA=50° )

由统计结果可知, 当SZA为50° 时, 使用季均BRDF形状参数在常绿阔叶林区域产生的绝对反演误差, 最大不超过0.077, 平均为0.062; 在90%的草地、 城镇和耕地区域分别产生最大0.171、 0.113、 0.179, 平均0.128、 0.097、 0.116的绝对反演误差; 在裸土区域则会产生最大0.226的绝对反演误差。

如表5所示, p1对反演误差的大小起决定性作用, 其值越大, 误差越大。 当p1为0.05时, 不同的AOD条件下均能获得较低的绝对反演误差, 但低AOD真值的相对误差可能非常大。 需要注意的是, 在大太阳天顶角条件下(SZA=80° ), 随着p1的增加, 当AOD真值变大, 绝对反演误差显著增加。 AOD的绝对反演误差与AOD真值并不是简单的线性关系, 在不同的观测几何、 地表类型和p1条件下, 上述二者可能存在完全相反的变化趋势。 例如, 当p1=0.15, SZA=50° 时, AOD绝对反演误差与真值成反比, 但当SZA=80° 时, AOD绝对反演误差与真值成正比。 AOD的相对反演误差表现出更明确的趋势, 即随着AOD真值的增加, 相对反演误差递减, 这与AOD反演时面对的普遍问题一致— — 当AOD真值较小时, 反演存在更大的不确定性[21], 此时地表估计的不确定性是构成AOD反演不确定性的主要来源。

使用季均BRDF参数, 对于地表信号占主导的标量卫星气溶胶反演, 存在不可避免的不确定性。 通过使用大气信号占主导的偏振观测减弱地表不确定因素, 或使用多角度观测实现BRDF和AOD的协同反演, 是未来提高气溶胶反演精度的重要方向, 采用国产多角度偏振传感器提供的多角度偏振观测信息或能克服这一关键问题。

4 结论

针对使用季均BRDF形状参数作为地表先验知识进行AOD反演可能造成的误差进行了评估, 首先统计了不同地表覆盖类型下BRDF形状参数的季均值, 再通过对确定的统计范围进行随机抽样以生成样本数据集, 最后使用样本数据集模拟的表观反射率进行AOD反演, 根据上述统计结果以及AOD反演误差的分析我们发现:

(1)几乎所有森林类地表(包括常绿针叶林, 常绿阔叶林, 落叶阔叶林以及混交林)的p1小于0.05, 近90%的草地类(包括郁闭灌木林, 稀疏灌木林, 有林草地, 稀树草原, 草地)、 耕地以及城镇的p1小于0.1, 几乎所有的裸地p1都大于0.05。 在高纬度区域, BRDF形状参数随时间的变化更剧烈, 因此在高纬度地区反演AOD时使用季均值代表地表情况, 会造成更大的反演误差。

(2)随着太阳天顶角与p1的增加, 使用季均BRDF形状参数对模拟表观反射率带来的误差也随之增加, 不同季节, 不同地表类型下模拟表观反射率的误差在观测几何、 AOD以及p1条件相同的情况下存在明显趋势, “ 森林” 类型的误差一般大于其他地表类型, 而“ 裸地” 类型的误差则总处于最低值。 另一方面, 模拟表观反射率的误差与AOD呈正相关, 随着AOD的升高, 模拟表观反射率的误差递增。

(3)不同观测几何、 p1条件下使用季均BRDF形状参数所带来的AOD反演误差表明, 当p1较小时, 随着观测几何与AOD条件的改变, AOD的绝对反演误差均较小, 即常绿阔叶林区域(p1≤ 0.05)的平均绝对反演误差不大于0.066, 近90%草地类、 耕地以及城镇区域(p1≤ 0.1)的平均绝对反演误差不大于0.183。 但随着p1的增加, AOD反演误差显著增大, 裸地区域(p1≥ 0.1)的平均绝对反演误差, 最高可达0.449。 因此, 在绝大部分植被覆盖度较高的地区, 使用季度平均值作为该地区的BRDF形状参数可以满足AOD反演的精度, 但亮地表区域使用季均结果会对AOD反演带来较大的误差。

参考文献
[1] Rabha S, Saikia B K. In Hand book of Nanomaterials in Analytical Chemistry, Elsevier, 2020, 449. [本文引用:1]
[2] Guo J, Deng M, Lee S S, et al. Journal of Geophysical Research: Atmospheres, 2016, 121(11): 6472. [本文引用:1]
[3] Stocker R F, Qin D, Plattner G K, et al. Climate Change 2013: The Physical Science Basis. Cambridge University Press. U. K. , 2013. [本文引用:1]
[4] Wang Y, Lee K H, Lin Y, et al. Nature Climate Change, 2014, 4(5): 368. [本文引用:1]
[5] He Q, Huang B. Remote Sensing of Environment, 2018, 206: 72. [本文引用:1]
[6] Pope C A, Ezzati M, Dockery D W. The New England Journal of Medicine, 2009, 360(4): 376. [本文引用:1]
[7] Dubovik O, Fuertes D, Litvinov P, et al. Frontiers in Remote Sensing, 2021, 2: 706851. [本文引用:1]
[8] Hsu N C, Tsay S C, King M D, et al. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(3): 557. [本文引用:1]
[9] Levy R C, Mattoo S, Munchak L A, et al. Atomspheric Measurement Techniques, 2013, 6(11): 2989. [本文引用:1]
[10] Lyapustin A, Martonchik J, Wang Y, et al. Journal of Geophysical Research: Atmospheres, 2011, 116(D3): doi: DOI:10.1029/2010JD014985. [本文引用:2]
[11] Lyapustin A, Wang Y, Laszlo I, et al. Journal of Geophysical Research: Atmospheres, 2011, 116(D3): doi: DOI:10.1029/2010JD014986. [本文引用:3]
[12] Yang L, Xue Y, Guang J, et al. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1629. [本文引用:4]
[13] Vermote E F, Tanré D, Deuze J L, et al. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(3): 675. [本文引用:1]
[14] She L, Xue Y, Yang X, et al. IEEE Transactions on Geoscience and Remote Sensing. 2018, 57(3): 1489. [本文引用:2]
[15] Qin Y, Mitchell R, Forgan B W. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(11): 6163. [本文引用:3]
[16] Schaaf C B, Gao F, Strahler A H, et al. Remote sensing of Environment, 2002, 83(1-2): 135. [本文引用:2]
[17] Vermote E, Justice C O, Bréon F M. IEEE Transactions on Geoscience and Remote Sensing, 2008, 47(3): 898. [本文引用:2]
[18] Bréon F M, Vermote E. Remote Sensing of Environment, 2012, 125: 1. [本文引用:2]
[19] Li Z, Guo J, Ding A, et al. National Science Review, 2017, 4(6): 810. [本文引用:1]
[20] Shi S, Cheng T, Gu X, et al. Remote Sensing of Environment, 2017, 195: 130. [本文引用:1]
[21] Thomas G E, Carboni E, Sayer A M, et al. Oxford-RAL Aerosal and Cloud (ORAC): Aerosol Retrievals From Satellite Radiometers, in Satellite Aerosol Remote Sensing Over Land , 2009, 193. [本文引用:2]