引用本文
李敏, 殷雄, 刘雪婧, 马世一, 周延, 种道彤, 熊兵, 李锟. 基于紫外光谱的油气两相流含气率检测研究[J]. 光谱学与光谱分析, 2025,45(2): 522-531.
LI Min, YIN Xiong, LIU Xue-jing, MA Shi-yi, ZHOU Yan, CHONG Dao-tong, XIONG Bing, LI Kun. Study on Detection of Gas Void Fraction in Oil-Gas Two-Phase Flow Based on Ultraviolet Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2025,45(2): 522-531.
Doi:10.3964/j.issn.1000-0593(2025)02-0522-10  
Permissions
Copyright©2025, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于紫外光谱的油气两相流含气率检测研究
李敏1, 殷雄1, 刘雪婧1, 马世一1, 周延1,*, 种道彤1, 熊兵2, 李锟2
1. 西安交通大学能源与动力工程学院, 陕西 西安 710049
2. 中国航发四川燃气涡轮研究院, 四川 成都 610500
*通讯作者 e-mail: yan.zhou@mail.xjtu.edu.cn

作者简介: 李 敏,女, 1995年生,西安交通大学能源与动力工程学院硕士研究生 e-mail: 3122303048@stu.xjtu.edu.cn

收稿日期: 2024-01-14 接受日期: 2024-04-28
基金: 国家重点研发计划项目(2021YFE0112800),陕西省企业院所联合重点专项(2023-LL-QY-29)资助
摘要

发动机润滑油系统中油气两相流含气率的检测对工业过程的安全运行有重要意义, 准确和快速地测量出含气率对监控发动机的运行状态尤为重要。 鉴于传统含气率检测方法的局限性, 提出一种紫外光谱结合建模算法预测含气率的方法。 首先, 在波长为185~430 nm的光谱范围内, 在5个不同两相流温度、 3个不同两相流流速下共15个工况下, 分别采集31组含气率范围在0.9%~3%的吸收光谱数据, 光谱波长变量为1 799个。 对光谱数据采用光谱-理化值共生距离算法(SPXY)将数据集划分为21组校正集, 10组测试集, 对不同含气率工况进行偏最小二乘(PLS)建模, 得到测试集决定系数( R2)范围为0.63~0.91。 针对不同工况预测效果差别过大的问题, 采用中心化(center)、 标准化(autoscaling)、 SG卷积平滑、 多元散射校正(MSC)、 标准正态变量变换(SNV)、 去趋势算法(Detrend)、 OPLS正交信号校正等数据预处理矫正方法优化模型, 得到Detrend-center-PLS模型预测效果最好, 其中 R2由0.903 2提高到0.955 7。 针对光谱波长变量过多的问题, 选取竞争性自适应加权算法(CARS)、 蒙特卡洛无信息变量消除算法(MCUVE)和遗传算法(GA)三种方法进行波段降维, 对降维后的光谱数据分别进行多元线性回归(MLR)、 偏最小二乘和最小二乘支持向量机(LS-SVM)建模, 得到预测结果最优为Detrend-center-CARS-PLS模型, 与全波段模型比较, R2从0.955 7提升到0.959 8。 由于优化效果并不显著, 对三种降维方法取交集, 重新进行建模, R2从0.959 8提升到0.967 1, 优化效果有所提升。 考虑到温度和流速对预测模型的影响, 建立多工况含气率预测模型, 采用与单工况相同的建模流程, 得到autoscaling为最优预处理方法, 且autoscaling-PLS模型的 R2为0.948 8, 波段降维方法将1 799波长变量消减到400~500个变量, 降维效果明显。 针对不同的建模方法, 得到autoscaling-MCUVE-LS-SVM模型为多工况最佳预测模型, R2达到0.992 6。 最后, 通过对比单工况预测模型和多工况预测模型, 得知多工况预测模型含气率预测效果优于单工况模型, 能改善模型预测效果。 结果表明, 采用光谱分析法结合建模算法预测油气两相流含气率是具备可行性的, 为发动机的安全运行提供了有效的监控方法。

关键词: 紫外光谱; 含气率; 两相流; 发动机
中图分类号:TK314 文献标志码:A
Study on Detection of Gas Void Fraction in Oil-Gas Two-Phase Flow Based on Ultraviolet Spectroscopy
LI Min1, YIN Xiong1, LIU Xue-jing1, MA Shi-yi1, ZHOU Yan1,*, CHONG Dao-tong1, XIONG Bing2, LI Kun2
1. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
2. AECC Sichuan Gas Turbine Establishment, Chengdu 610500, China
*Corresponding author
Abstract

The accurate and rapid measurement of the gas void fraction in the oil-gas two-phase flow of the engine lubrication system holds significant importance for ensuring the safe operation of industrial processes. The precise determination of the void fraction is particularly crucial for monitoring the operational status of the engine. In light of the limitations associated with traditional gas void fraction detection methods, a method is proposed that combines ultraviolet spectroscopy with a modeling algorithm for predicting the void fraction. Initially, within the range of 185 to 430 nm, 31 sets of absorption spectra data were collected at five different two-phase flow temperatures and three different two-phase flow velocities, encompassing 15 operational conditions. The spectra were obtained for gas void fractions ranging from 0.9% to 3%. A total of 1799 spectral wavelength variables were considered for analysis. The spectral-physicochemical value coexistence distance algorithm (SPXY) was employed to partition the spectral data set into 21 calibration and 10 test sets. Partial least squares (PLS) modeling was conducted for various gas void fraction conditions, resulting in a test set determination coefficient R2) range of 0.63 to 0.91. To address the significant variations in prediction performance across different operating conditions, various data preprocessing methods, including centering, autoscaling, Savitzky-Golay convolution smoothing, multiplicative scatter correction (MSC), standard normal variate (SNV) transformation, detrending, and orthogonal partial least squares (OPLS) orthogonal signal correction, were applied to optimize the model. The Detrend-center-PLS model exhibited the best predictive performance, with the R2 increasing from 0.903 2 to 0.955 7. To address the issue of excessive spectral wavelength variables, three methods, Competitive Adaptive Reweighted Sampling (CARS), Monte Carlo Uninformative Variable Elimination (MCUVE), and Genetic Algorithm (GA), were employed for band dimension reduction. The reduced spectral data were then modeled using Multiple Linear Regression (MLR), Partial Least Squares, and Least Squares Support Vector Machine (LS-SVM). The optimal predictive model was determined to be the Detrend-center-CARS-PLS model, which exhibited an improved R2 from 0.955 7 to 0.959 8 compared to the full-wavelength model. Due to the limited improvement in optimization, the intersection of the three-dimensionality-reduction methods was taken, and the modeling was re-conducted. The R2 increased from 0.959 8 to 0.967 1, indicating a noticeable enhancement in optimization. Considering the influence of temperature and flow rate on the predictive model, a multi-condition gas void fraction prediction model was established using the same mprocess as the single-condition model- Autoscaling was identified as the optimal preprocessing method, and the R2 for the autoscaling-PLS model was 0.948 8. The wavelength dimensionality reduction method reduced the 1799 wavelength variables to 400~500 demonstrating a significant dimensionality reduction. For different modeling methods, the autoscaling-MCUVE-LS-SVM model was identified as the best multi-condition predictive model, achieving an R2 of 0.992 6. Finally, by comparing the single-condition predictive model with the multi-condition predictive model, it was found that the gas void fraction prediction performance of the multi-condition model was superior, improving overall predictive accuracy. The results indicate that using spectral analysis combined with modeling algorithms for predicting gas void fraction in oil-gas two-phase flow is feasible and provides an effective monitoring method for the safe operation of engines.

Keyword: Ultraviolet spectrum; Gas void fraction; Two-phase flow; Engine
引言

发动机对工业过程的安全运行以及运行效率具有至关重要的意义, 因此需要快速、 准确、 有效地监控发动机的运行状态。 而润滑油系统作为发动机中的重要组成部分, 承担着润滑、 冷却、 密封和清洁等重要作用。 在实际工业应用中, 空气会在发动机运行过程中进入润滑油系统, 与润滑油混合形成油气两相流, 影响润滑油的润滑特性, 进而影响整个发动机的正常运行。 含气率作为油气两相流最重要的参数和特征之一, 影响着润滑系统中回油泵的回油效率以及回油管路散热器的散热特性[1]。 因此, 有关发动机润滑油系统中油气两相流含气率的准确和快速测量研究具有重要意义。 目前国内外常用的测量气液两相流含气率的方法大致可分为离线检测和在线检测两类方法。

其中, 离线检测方法主要是快关阀门法, 该方法被广泛应用于气液两相流的含气率测量中, 刘起超研究不同振动和流动工况下垂直上升管气液两相流的含气率特性, 采用快关阀方法测量平均截面含气率[2]。 由于该方法需要人为操作, 不适用于复杂实验装置结构以及含气率的在线测量。

在线检测方法主要有射线法、 超声波法、 电学法、 高速摄影法等[3, 4, 5]。 程洁[6]使用射线法对高温高压下垂直管束间气液两相流截面含气率的分布规律进行了实验研究, 该研究对蒸汽发生器的结构设计和流动特性研究具有重要意义。 张理[7]采用射线法, 测量常温常压垂直上升管内气水两相流截面含气率, 得到的测量值与理论计算值吻合很好, 相对偏差较小。 Zych[8]利用射线法对气液两相流参数进行测量时, 利用4种降噪算法对探测信号中的随机噪声进行处理。 但射线法测量成本较高, 且射线对人体有害等原因使得工业中射线法测含气率的应用受到限制。 李涛[9]基于水平直管气液两相流的经典L-M(Lockhart-Martinelli)截面含气率模型, 建立了双声道平行直射式超声波流量计湿气虚高预测模型。 得到的预测模型的整体相对误差在± 6%以内。 方立德[10]使用阵列超声传感器探究了气液两相流界面下的超声波声束和液面的关系, 实现了超声波声束对整个气液两相流界面的参数检测, 重构图像得到的截面含气率和高速相机拍摄得到的截面含气率误差不超过4%。 由于两相或多相流的复杂动力学特性, 利用超声波原理进行含气率测量的研究仍在不断改进和研究中。 He[11]开发了多线电容探头测量气液分层两相流中含气率的装置, 能够测量局部含气率和平均含气率。 电学法对两相流流型和各相的占比有适用要求, 受流型和温度的影响较大, 因此该方法在广泛应用之前仍需研究和改进。 王腾[12]采用高速摄影法, 对光纤探针测量泡状两相流局部含气率的精度进行了试验研究。 刘帅[13]基于高速摄影仪和自主开发的丝网传感器测量技术, 研究了气液两相流流型从无旋状态转变为螺旋状态前后的流型特征及含气率时空分布特性。 而高速摄影法为避免图像失真, 要求两相流的各相速度较低, 并且相界面处光线的反射和折射, 会影响结果的正确性。

光谱分析法属于在线检测方法, 在化学分析、 环境检测、 生物医学、 食品质量、 材料科学、 大气科学和地质学等多个领域均得到广泛应用[14, 15, 16]。 在两相流含气率检测领域, 周延采用偏最小二乘回归模型结合近红外光纤光谱仪对润滑油油气两相流含气率的测量进行了研究, 研究结果表明, 该方法可实现油气两相流中润滑油中含气率的测量, 预测模型决定相关系数达到0.981[17]。 Wang[18]通过分析水在近红外光下的特征吸收波段, 建立了不同工况下的含气率测量模型。 方立德[19]提出了一种新的含气率测量装置, 将近红外发射装置安装在流体流动方向, 实现含气率的准确测量。 谢辰[20]应用差压-近红外组合测量装置, 实现对不同流型下两相流的含气率的测量。

光谱分析法在气液两相流含气率测量中的研究目前相对较少, 但通过前人的研究可知, 该方法对含气率的测量具备一定的可行性。 光谱分析法具有非侵入性、 实时监控、 高灵敏度、 响应速度快和远距离测量等优点, 这些优点使其在发动机润滑油系统中油气两相流含气率的测量中发挥着重要的作用, 本研究基于紫外光谱检验该方法的可行性并通过建立模型分析其含气率检测效果。

1 实验部分
1.1 基本原理

光谱检测技术适用于油气两相流含气率测量的理论基础就是比尔-朗伯(Beer-Lambert)定律。 该定律描述的是当光源发出的一束平行单色光垂直通过某一均匀非散射的待测物质时, 光强会发生衰减, 待测物质的吸光度与物质的含量c及物质吸收层厚度l成正比。

Aλ=-lgII0=ελlc(1)

式(1)中: Aλ 为待测物质在波长λ 处的吸光度; I为出射光强; I0为入射光强; ε λ 为吸光系数; l为吸光厚度, mm; c为吸光物质的含量。

在油气两相流含气率吸光度测量实验中, 当光通过流体中的气、 液两相流体时, 光强会有不同程度的衰减, 衰减前后的光强之比与光线路径上的气泡的形状及大小之间有相对应的关系, 进而测量实验管道中两相流的含气率。

1.2 光谱数据采集系统

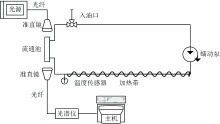
紫外吸收光谱数据采集系统由光源、 光纤、 光谱仪、 准直镜、 流通回路和光谱数据接收设备组成。 其中, 光源选用美国Ocean Insight公司的氘灯-钨灯组合式光源, 型号为DH-2000-DUV, 能够发射190~2 500 nm波段的光线; 光纤选用Ocean Insight公司的QP600-1-SR光纤; 光谱仪选用荷兰Avantes公司生产的AvaSpec-USBi2048L光谱仪, 光谱仪的波长检测范围为185~430 nm, 分辨率为0.2~0.29 nm; 流通回路由流通池、 流通管道、 温度传感器、 加热带和蠕动泵组成, 蠕动泵选用的纽凯蠕动计量泵BR-8000。 光谱采集系统如图1所示。

图1 紫外吸收光谱采集系统Fig.1 Ultraviolet absorption spectroscopy data collection system

1.3 数据分析

吸收光谱实验对含气率在0.9%~3%范围内的油气两相流进行, 以0.07%为间隔采集31组含气率不同光谱数据。 考虑到温度和流速对光谱数据的影响, 在每个含气率下, 设置了5个两相流温度: 室温(27 ℃)、 30 ℃、 40 ℃、 50 ℃、 60 ℃和3个两相流流速: 5.1、 7.7 、 10.2 m· min-1, 共15个工况的光谱数据采集。 每个工况下不同油气两相流含气率的数据集结构为: 吸光度矩阵大小为31× 1 799, 包含31个样本和1 799个波长变量。

图2为在27 ℃、 5.1 m· min-1流速工况中的含气率为0.9%、 1.39%、 1.95%、 2.51%和3%的油气两相流在紫外波段的吸收光谱及吸光度与含气率的相关系数图。 计算了采集的31个样本吸收光谱中不同波长对应的吸收强度值与含气率之间的相关系数r, 如图2(b)所示。

图2 油气两相流在紫外波段的吸收光谱及r图
(a): 吸收光谱; (b): 相关系数Fig.2 Absorption spectra and r plot of oil-gas two-phase flow in the ultraviolet range
(a): Absorption spectra; (b): Correlation coefficient

由图2(a)可见油气两相流在紫外波段有吸收, 但其吸光度与含气率之间没有直观线性关系。 由图2(b)可知单波长吸光度与含气率变化的相关性较差, 相关性主要表现在215~275 nm波长范围内, 其中, 251.950 1 nm处r存在最大值, 为0.655 4。 由上述结果看, 油气两相流虽然在紫外波段存在吸光区域, 但线性相关性较差, 单波长光谱信息量少, 光谱噪声信息含量大。 因而需要利用多波长点光谱数据进行建模, 综合考虑各波长点处的信息。

1.4 光谱数据处理

在含气率预测模型建模前, 首先, 需要利用不同的划分方法, 将光谱数据分为校正集和测试集, 校正集中样本用来建立测量校正模型, 测试集中样本用来检验所建立模型的预测能力; 然后, 通过对原始光谱数据矩阵进行数据预处理,

去除数据中的噪声、 干扰和异常值, 提取有用的光谱信息; 最后, 通过对预处理后的数据进行波段降维, 在保证模型预测精度的前提下, 降低数据维度, 简化含气率预测模型。

1.4.1 样本数据集划分

常用的样本分类的方法有: 随机法、 百叶窗法、 K-S法、 SPXY法等。 随机法和百叶窗法对数据不进行挑选, 不能保证选择出具有代表性的样本和所建模型的外推能力。 K-S法是根据欧式距离的大小在样本集中依次挑选样本进入校正集, 直至达到所要求的样本数, 其优点是能保证样本有分布均匀的空间距离。 而SPXY法是K-S法的改进, 其在计算样本间距离时将光谱矩阵和参数矩阵同时考虑在内, 确保了样本在两个空间中具有相同的权重, 覆盖了多维向量空间, 改善校正集所建模型的预测能力。 本研究中样本选择方法选用SPXY法。

1.4.2 数据预处理矫正

光谱分析中的建模误差很大部分都来自于光谱数据中的噪声, 这是由于光谱数据会受到光谱测量时的环境条件、 光谱仪工作状态等因素的影响, 因此, 在建模前, 利用数学方法对原始光谱的吸光度数据进行合适的预处理, 消除影响建模效果的噪声。

选用中心化(center)、 标准化(autoscaling)、 SG卷积平滑、 多元散射校正(MSC)、 标准正态变量变换(SNV)、 去趋势算法(Detrend)、 OPLS正交信号校正等预处理矫正方法, 分析对比得出最优数据预处理方法。

1.4.3 波段降维

紫外波段的光谱数据中含有上千个波长变量, 采用全部波段进行多元校正建模, 计算工作量庞大, 且部分光谱区域存在样本间的有效光谱数据差异小、 光谱严重重叠、 不同波长的光谱数据多重相关、 光谱的信噪比低等问题, 需要用波段降维方法选取出最优的光谱变量组合, 提高建模效率。

选取竞争性自适应加权算法(CARS)、 蒙特卡洛无信息变量消除算法(MCUVE)和遗传算法(GA)三种波段降维方法并进行对比分析。

1.5 含气率预测建模

选取多元线性回归(MLR)、 偏最小二乘(PLS)和最小二乘支持向量机(LS-SVM)三种建模方法, 通过对比分析三种模型的预测效果选择最优的两相流含气率预测模型。 建模流程如图3所示。

图3 油气两相流含气率预测模型建模流程图Fig.3 Modeling flowchart of gas void fraction prediction model for oil-gas two-phase flow

1.6 模型评价指标

对于紫外波段光谱数据所建立的油气两相流含气率预测模型以及模型的含气率预测效果需要选取一些评价指标进行结果评估。 本研究选取的评价指标有如下三个: 测试集预测均方根误差(root-mean-squares error of prediction, RMSEP)、 校正集交互验证均方根误差(root-mean-squares error of cross-validation, RMSECV)和决定系数(coefficient of determination, R2)。 其中, RMSEP值越小, 表明模型的预测能力越好; RMSECV值越小, 说明模型的回归程度越好; R2值越接近于1, 说明模型的回归或预测结果越好。

2 结果与讨论
2.1 不同两相流工况的PLS建模效果

由于单波长光谱数据无法良好地解释含气率的变化, 采用PLS建模法对紫外波段中不同工况的光谱数据分别进行建模分析, 对比分析不同模型, 观察两相流温度和流速对模型建模效果的影响。 采用SPXY方法将每个工况中校正集个数划分为21个, 测试集个数划分为10个。 对紫外波段中15个工况建立的油气两相流含气率的PLS结果如表1所示。

表1 紫外波段不同工况的PLS含气率模型比较 Table 1 Comparison of PLS Gas void fraction models under different conditions in the ultraviolet range

表1中的R2反映含气率预测模型拟合程度的评价指标, 该值越接近于1, 不同波长吸光度对含气率的解释关系越佳, 预测效果越好。 图4中为不同工况下, 模型测试集R2的变化情况, 图4(a)和图4(b)分别为工况中两相流温度和流速改变时, 测试集R2的变化情况。

图4 不同工况下测试集决定系数R2的变化情况
(a): 改变温度; (b): 改变流速Fig.4 Variation of test set determination coefficient R2 under different conditions
(a): Temperature change; (b): Velocity change

由图4可知, 紫外波段中不同工况含气率模型的预测效果不同, 测试集R2范围为0.63~0.91, 有11个工况R2大于0.8, 其中, 温度为40 ℃、 流速为10.2 m· min-1工况点的含气率预测效果最差R2仅有0.633 6。 由图4(a)可知, 在60 ℃时, 三个工况点的模型测试集R2数值接近。 由图4(b)可知, 除去个别工况点, 可以看出两相流流速越大, 模型的测试集R2越小, 预测效果变差。

2.2 单工况含气率优化模型

从紫外波段15个不同工况的PLS含气率预测模型R2可以看出, 只使用PLS方法建模得到的模型预测效果并不是很好, 因此, 选取温度为30 ℃、 流速为5.1 m· min-1工况的数据集建立优化的含气率预测模型, 观察模型预测效果的改善程度。

2.2.1 数据预处理

采用center、 autoscaling、 SG、 MSC、 SNV、 Detrend、 OPLS等数据预处理矫正方法, 对含气率样本的原始光谱进行预处理, 对预处理后的光谱数据进行PLS建模分析, 其结果如表2所示。

表2 不同预处理方法结合PLS的油气两相流含气率预测模型比较 Table 2 Comparison of gas void fraction prediction models for oil-gas two-phase flow using different preprocessing methods combined with PLS

从表2可知, PLS结合Detrend和center所建立的模型对油气两相流含气率的预测效果优于PLS结合其他预处理方法或原始光谱数据所建立的模型。 Detrend-center-PLS模型与PLS模型比较, 测试集决定系数R2从0.903 2提高到0.955 7, 测试集均方根误差RMSEP从0.175 8减小到0.119 0, 潜变量数从11减少到10, 提高了预测效果, 简化了模型。 在建模过程中, 采用SG进行光谱平滑和OPLS方法进行数据正交信号校正时建模情况相对于原始数据的模型来说, 效果均不明显, 而采用Detrend、 SNV和MSC预处理方式均能不同程度的提高模型的预测效果, 说明动态油气两相流的原始光谱中由于散射引起的光谱变化基线漂移对含气率的检测有较大影响。 而Detrend、 SNV和MSC方法均在基线校正、 去除基线漂移方面有不同效果。

2.2.2 特征波长变量选择及建模

选取最佳预处理方法Detrend-center后, 采用CARS、 MCUVE和GA算法对1 799个波长变量进行选择。 其中, 利用CARS算法共选择1 200个特征波长变量, 利用MCUVE算法共选择1 180个特征波长变量, 利用GA算法共选择1 457个特征波长变量。 三种算法选择的特征波长变量分布如图5所示。

图5 不同算法选择的特征波长分布Fig.5 Distribution of feature wavelengths selected by different methods

分别对未选择的紫外波段光谱数据和三种算法选择后的光谱数据进行MLR、 PLS和LS-SVM建模。 建模结果如表3所示。

表3 不同油气两相流含气率校正模型的校正和预测结果 Table 3 Correction and prediction results of different gas void fraction correction models for oil-gas two-phase flow

由表3知, 对紫外波段的波长变量进行选择, 并分别建立校正模型的结果对比中, CARS, MCUVE、 GA三种方法的变量选择个数均大于1 000, 波长变量的筛选力度并不大。 将MLR、 PLS、 LS-SVM三种建模方法比较来看: 模型校正效果, MLR最优, PLS次之, LS-SVM最差, 但R2都达到0.95以上; 但MLR模型的预测效果比PLS、 LS-SVM模型要差一些, LS-SVM次之, PLS最优。

建模结果最优的Detrend-center-CARS-PLS模型与全波段Detrend-center-PLS模型比较来看, 优化效果并不显著, 且变量筛选力度不大。

为此, 对三种波长选择方法的变量选择结果取交集, 交集中的变量共有720个, 再结合MLR、 PLS和LS-SVM方法进行建模分析。 表4所示的是变量交集中720个波长变量的建模结果。

表4 变量交集的含气率校正模型的校正和预测结果 Table 4 Correction and prediction results of gas void fraction correction models with intersection variables

由表4中可知, 总体来说, 选取CARS, MCUVE、 GA三种变量选择结果交集中的变量进行建模的效果要比单独采用三种中任一种方法进行变量选择的效果要好。 其中PLS模型和LS-SVM模型的总体效果较好一些, 测试集R2均达到0.96以上, LS-SVM校正模型的预测效果较好于PLS模型, 而PLS模型的校正结果优于LS-SVM模型。

2.3 多工况含气率优化模型

对每个工况都单独建立含气率预测模型的话, 需要大量的模型, 并且单工况含气率预测模型并未考虑到温度和流速的连续性。 因此, 需要建立一个适用于不同温度和流速工况的含气率预测模型。

2.3.1 数据预处理

对紫外波段内含有温度和流速信息的数据集进行构造: 将两相流光谱矩阵增加两列温度和流速信息, 即将温度值作为自变量矩阵的第1 800列, 流速值作为自变量矩阵的第1 801列。 由于紫外波段共有465个实验数据样本, 因此紫外波段含气率检测的吸光度矩阵大小为465× 1 801, 含气率矩阵大小为465× 1。 采用SPXY划分方法将数据集划分为315个校正集, 150个测试集。 采用与单工况相同的预处理方法进行光谱数据的预处理, 建立PLS模型进行比较, 结果如表5所示。

表5 不同预处理方法结合PLS的油气两相流含气率预测模型比较 Table 5 Comparison of gas void fraction prediction models for oil-gas two-phase flow using different preprocessing methods combined with PLS

由表5中数据看出, autoscaling为最优预处理方法, 采用autoscaling预处理能够使得各变量具有相同的尺度, 能增强模型的校正和预测效果。 并且, autoscaling-PLS含气率预测模型中, 校正集R2为0.973 3, 校正集RMSECV为0.104 6, 测试集R2为0.948 8, 测试集RMSEP为0.126 1, 模型效果较好, 可以在紫外波段建立包含不同温度和流速信息的油气两相流含气率模型。

2.3.2 特征波长变量选择及建模

选取最佳预处理方法autoscaling后, 采用CARS、 MCUVE和GA算法对特征波长变量进行选择, 分别选择了473、 415和486个特征波长。 图6为三种算法选择的特征波长分布。

图6 不同算法选择的特征波长分布Fig.6 Distribution of feature wavelengths selected by different algorithms

分别对autoscaling预处理后的未进行选择的全部变量数据和三种算法选择后的特征变量数据进行MLR、 PLS和LS-SVM建模。 表6为建模结果。

表6 不同油气两相流含气率校正模型的校正和预测结果 Table 6 Correction and prediction results of different gas void fraction correction models for oil-gas two-phase flow

由表6中数据可以看出, 进行变量选择后变量的个数都处于400~500的范围, 降维效果明显。 而且削减变量数目后的PLS和LS-SVM模型相比较于全变量建模中的相应模型, 其校正集和测试集的R2和RMSECV(RMSEP)基本都处于同一水平, 说明简化了模型, 但并没有改善模型预测效果。

比较表6中不同模型的建模效果, 发现LS-SVM模型的测试集预测效果最好, 测试集R2均大于0.99。 而在所有LS-SVM模型中, autoscaling-MCUVE-LS-SVM模型中变量个数最少, 为415个, 且测试集R2为0.992 6, 与全波段变量建模的autoscaling-LS-SVM模型比较, 模型预测效果相差不大。 因此选取autoscaling-MCUVE-LS-SVM模型为不同温度和流速下油气两相流含气率的最优检测模型。 该模型的预测效果图如图7所示。

图7 autoscaling-MCUVE-LS-SVM预测效果图Fig.7 Effectiveness chart of autoscaling-MCUVE-LS-SVM prediction model

2.4 含气率预测模型效果对比

通过分别建立紫外波段中温度为30 ℃、 流速为5.1 m· min-1工况的含气率预测优化模型和多工况的含气率预测优化模型分析得知, 单工况模型的测试集R2为0.969 1, RMSEP为0.099 4; 多工况模型的测试集R2为0.992 6、 RMSEP为0.047 9, 后者模型的含气率预测效果好于前者。

将紫外波段中该模型的测试集中的样本按照工况的不同, 分为15个测试集, 利用autoscaling-MCUVE-LS-SVM模型进行每个工况的预测效果验证, 将结果与单工况PLS模型预测结果对比, 比较不同工况的测试集R2和RMSEP值, 比较结果如表7。

表7 紫外波段不同工况的预测效果对比 Table 7 Comparison of prediction performance under different conditions in the ultraviolet range

图8为多工况模型在不同温度和流速工况下, 测试集R2的变化情况, 图8(a)和图8(b)分别为工况中两相流温度和流速改变时, 测试集R2的变化情况。

图8 不同工况测试集决定系数R2的变化情况
(a): 改变温度; (b): 改变流速Fig.8 Variation of test set determination coefficient R2 under different conditions
(a): Temperature change; (b): Velocity change

从图8可以看出, 紫外波段中每个工况下的含气率预测效果得到不同程度的改善, 有11个工况下的测试集R2的值都大于0.99, 两相流温度为室温和60℃时, 测试集R2值略小, 模型的预测效果稍差。

3 结论

针对发动机润滑油系统的安全运行检测问题, 提出了一种紫外光谱结合建模算法建立油气两相流含气率的检测方法。 通过紫外光谱实验系统, 采集油气两相流含气率在0.9%~3%范围下的光谱实验数据, 对不同工况两相流含气率进行PLS建模预测, 分析模型预测结果的精确性。 通过不同的数据预处理方法、 波长选择方法和建模方法先后进行单工况含气率优化模型和多工况含气率优化模型的建模, 对比两种模型的含气率预测效果, 得知单工况最优模型Detrend-center-CARS-PLS的测试集R2为0.969 1, 多工况最优模型autoscaling-MCUVE-LS-SVM的测试集的R2为0.992 6, 可见多工况预测模型在考虑到温度和流速的影响下, 含气率预测效果优于单工况模型, 并在一定程度上改善了模型的预测效果。 研究结果表明, 采用光谱分析法结合建模算法建立油气两相流含气率预测模型是具备可行性的, 对发动机润滑油系统的安全运行有着重要意义。

参考文献
[1] LI Shu, HU Jian-ping, TAN Yi, et al(李澍, 胡剑平, 谭逸, 等). Journal of Propulsion Technology(推进技术), 2024, 45(5): 130. [本文引用:1]
[2] LIU Qi-chao, ZHOU Yun-long, CHEN Cong(刘起超, 周云龙, 陈聪). CIESC Journal(化工学报), 2023, 74(6): 2391. [本文引用:1]
[3] Hernand ez-Alvarado F, Kleinbart S, Kalaga D V, et al. International Journal of Multiphase Flow, 2018, 102: 119. [本文引用:1]
[4] Park H J, Akasaka S, Tasaka Y, et al. IEEE Sensors Journal, 2020, 21(1): 273. [本文引用:1]
[5] Jahangir S, Wagner E C, Mudde R F, et al. International Journal of Multiphase Flow, 2019, 120: 103085. [本文引用:1]
[6] CHENG Jie, GUO Ya-jun, WANG Teng, et al(程洁, 郭亚军, 王腾, 等). CIESC Journal(化工学报), 2019, 70(4): 1375. [本文引用:1]
[7] ZHANG Li, SUI Zhi-qiang, ZHOU Xiang, et al(张理, 随志强, 周翔, 等). Mechanical and Electrical Equipment(机电设备), 2021, 38(3): 90. [本文引用:1]
[8] Zych M, Hanus R, Wilk B, et al. Measurement, 2018, 129: 288. [本文引用:1]
[9] LI Tao, YUAN Chao, QI Feng-feng, et al(李涛, 袁超, 齐锋锋, 等). Instrument Technique and Sensor(仪表技术与传感器), 2023, (7): 105. [本文引用:1]
[10] FANG Li-de, KONG Heng-zheng, HAN Bang-bang, et al(方立德, 孔恒正, 韩棒棒, 等). Acta Metrologica Sinica(计量学报), 2022, 43(12): 1616. [本文引用:1]
[11] He D H, Chen S L, Bai B F. Experiment Thermal and Fluid Science, 2019, 102: 61. [本文引用:1]
[12] WANG Teng, BI Qin-cheng, GUI Miao, et al(王腾, 毕勤成, 桂淼, 等). Journal of Engineering Thermophysics(工程热物理学报), 2022, 43(6): 1565. [本文引用:1]
[13] LIU Shuai, CHEN Cong, LIU Li, et al(刘帅, 陈聪, 刘莉, 等). Nuclear Power Engineering(核动力工程), 2022, 43(5): 43. [本文引用:1]
[14] DAI Pei-yu, ZHANG Xin, MAO Xing, et al(戴佩玉, 张欣, 毛星, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2023, 39(16): 160. [本文引用:1]
[15] YI Rong-nan, WU Yan, WANG Jun-li, et al(易荣楠, 吴燕, 王俊力, 等). Chinese Journal of Analytical Chemistry(分析化学), 2023, 51(2): 147. [本文引用:1]
[16] LIU Qiang, LIU Shao-bo, LU Xue-song, et al(刘强, 柳少波, 鲁雪松, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(9): 2679. [本文引用:1]
[17] Zhou Y, Cui H S. Measurement Science and Technology, 2023, 34(3): 035501. [本文引用:1]
[18] Wang C, Zhao N, Fang LD. Experimental Thermal and Fluid Science, 2016, 76: 98. [本文引用:1]
[19] FANG Li-de, LÜ Xiao-hui, TIAN Ji, et al(方立德, 吕晓晖, 田季, 等). China Measurement & Test(中国测试), 2018, 44(1): 21. [本文引用:1]
[20] XIE Chen, FANG Li-de, WANG Dong-xing(谢辰, 方立德, 王东星, 等). Metrology Science and Technology(计量科学与技术), 2018, 2: 3. [本文引用:1]