作者简介: 王 琦, 1978年生,运城学院数学与信息技术学院副教授 e-mail: wangqi_2048@outlook.com
光谱双星通常是指光谱中呈现双主导成分特征, 由于该双成分复杂多样, 其成因也多种多样, 同时光谱信噪比相对比较低, 现有许多分析方法将双成分系统光谱分离成两条光谱进行分析, 而分离方法无法保证光谱的准确性, 现有聚类方法的单次聚类可靠性比较低。 提出一种基于粗集与聚类投票机制的光谱双星分析与评估方法, 采用多次聚类和投票思想, 给出每条光谱属于相应类别的梯度可靠性。 该方法包含两个部分: ①采用不同思想的聚类算法, 将光谱双星数据集进行重构, 将每种聚类算法标签采用匈牙利算法将聚类标签对齐作为光谱属性, 从而重构数据集。 ②利用投票机制, 得票数反映聚类结果的一致程度, 获得每条光谱的类别, 定义粗集示踪每类光谱特征, 采用上/下近似集给出每条光谱所归类别的可靠性。 选择郭守敬望远镜(LAMOST) DR10发布光谱双星集作为分析对象, 采用基于划分的K-means、 基于模型的GMM(Gaussian mixture model)、 谱聚类(spectral clustering)和层次聚类(agglomerative clustering)四种聚类算法重构光谱数据集, 选择得票数下界 μ为2, 通过投票得到1、 0.75、 0.5为可靠性梯度的聚类结果。 其中大约1/3的样本可靠性为1, 说明这批样本的四种聚类结果完全一致; 对每类光谱和投票数的信噪比进行统计分析, 投票数低的样本的信噪比相对较低, 是它们被不同的聚类算法划分到不同类别的原因之一; 对可靠性为1的6类光谱样本进行了物理成因的分析, 其中以双星、 河内星云+目标恒星两种为主, 聚类标签的差异可能由于两种成分流量差异或拼接、 定标等数据处理所导致。 也有可能由于光谱质量较低导致pipeline误判的因素, 其天区位置分布与低质量数据分布特征的研究基本一致。
Spectral binary star usually refers to the spectra that show double dominant component characteristics. Due to the double component's complexity and diversity, its formation is complicated. At the same time, the spectral signal-to-noise ratio is relatively low. Many of the existing analytical methods separated two-component system spectra into two spectra. Still, the separation method can't guarantee the accuracy of the spectra, and the reliability of the existing clustering methods of the single clustering is relatively low. This paper proposes a binary star spectrum analysis and evaluation method based on a rough set and cluster voting mechanism. Using the idea of multiple clustering and voting, the gradient reliability of each spectrum belongs to the corresponding category. The method consists of two parts: First, the spectral binary star data set is reconstructed by using clustering algorithms with different ideas, and each clustering algorithm label is aligned with the Hungarian algorithm as a spectral attribute to reconstruct the data set. Secondly, the voting mechanism is used to reflect the consistency of the clustering results and give the category of each spectrum. At the same time, rough sets are defined to trace the characteristics of each spectrum, and the reliability of the classification of each spectrum is given by using the up/down approximation set. LAMOST DR10 was selected to publish the spectral set of binary stars as the analysis object. Four clustering algorithms, partition-based K-means, model-based Gaussian mixture model (GMM), Spectral clustering, and Agglomerative clustering, were used to reconstruct the spectral data set. Select the lower bound of votes as 2 and obtain clustering results with reliability gradients of 1, 0.75, and 0.5 through voting. About 1/3 of the samples have a reliability of 1, indicating that the four clustering results of this batch of samples are completely consistent. The SNR of each spectrum and the number of votes arestatistically analyzed. The SNR of the samples with the low number of votes is relatively low, which is one of the reasons why they are divided into different categories by different clustering algorithms. We analyzed the physical origin of 6 spectral samples with a reliability of 1, among which binary stars, Hanoi Nebula, and target stars were the main ones. The difference in clustering labels may be caused by the difference in the flow rate of the two components or data processing such as splicing and calibration. In addition, factors may lead to pipeline misjudgment due to low spectral quality, and its sky location distribution is consistent with the research on the distribution characteristics of low-quality data.
光谱双星通常是指光谱中呈现双主导成分特征, 其特征分析对恒星结构与演化、 数据处理与分析等研究具有重要的意义。 光谱呈现双主导成分的原因复杂多样, 比如双星系统, 受引力的束缚相互缠绕、 旋转, 其相互作用和性质对于理解恒星的形成、 演化[1, 2]具有重要意义; 如天光背景(尤其是亮月夜)残留, 解构残留成分对提高减天光质量极具意义[3]; 又如邻近光纤污染、 星云成分污染等[4, 5]。
光谱双星分析面临着一系列困难, 包括光谱线的重叠、 多重成分的存在、 数据噪声[6, 7]等的影响。 这些问题使光谱双星的分类、 特征提取和参数推测变得复杂而困难。 LAMOST数据处理pipeline通过模板匹配的方法识别出双星目标[8], 大多数对光谱双星分析需要先将光谱分解成两个恒星的光谱, 进而分析其轨道周期、 物理参数等[9, 10]。 光谱双星的类别与组成双主导成分的目标有关, 传统单一的聚类方法无法有效挖掘出其中复杂的特征[11, 12, 13, 14]。
采用基于粗集与聚类投票机制的聚类方法, 对LAMOST光谱双星进行分类, 对各类光谱双星从光谱特征、 图像特征以及背后可能的物理机制等方面进行了分析。
定义1 设S={s1, s2, …, sn}为光谱数据集, si表示一条光谱, 对于∀ s∈ S, s={x1, x2, …, xm, yk}, 其中xj称为在静止波长j处的流量, yk∈ T={t1, t2, …, tr}表示该光谱的类别, 由光谱类别集T可导出光谱数据集S的一个划分(等价关系)。
定义2 设集合S'={s'1, s'2, …, s'n}, 则聚类映射可定义为F: S→ S', 对于∀ s'∈ S', s'={c1, c2, …, cp, yk}, 其中ci∈ Ci为采用聚类算法i获取的候选类别, yk∈ T={t1, t2, …, tr}表示该光谱的类别。
当聚类映射F为满射, 且映射操作不改变光谱类别。 通过映射F, 光谱数据集的维度由m(原始光谱维度)降低到r(与采用聚类算法的个数有关), 且属性值也由数值型转变为类属性。
定义3 对于集合S'和等价关系R, X⊆S'表示任意光谱类别y∈ T的数据集合, [x]R表示x满足的候选类别集, [y]R表示类别y对应的候选类别集, 可以定义X在R下的上/下近似集, 见式(1)和式(2)
对于∀ s'∈ S', 由聚类映射的特点(至少有1次划分为某类), 可能出现在任意类别的上近似集R-(X)中, 若条件设置过于宽松, 与光谱聚类分析的初衷不一致。 基于投票机制, 采用投票数量为每条上近似集中的记录赋予可靠性度量, 式(2)可推广为
式(3)中, μ 为票数下界。
定义4 类别可靠性度量, 见式(4)
提出基于粗集和投票机制的光谱双星聚类模型(如图1所示, 图中左表是原始数据集, 上方框图是聚类算法集, 右表为重构数据集, 下方圆形表示带梯度可靠性的类别)。 该模型包含两个环节, (1)基于聚类算法的原始光谱数据集重构, 从而达到降维和离散化的效果; (2)基于粗集和投票机制的类别分析。
使用LAMOST DR10 v1.0发布的所有光谱双星, 一共6 626条, 经以下预处理后得到初始数据集S。
(1) 去掉光谱短波端λ < 4 000 Å 、 长波端λ > 8 650 Å 以及红蓝端拼接部分(5 700~5 900 Å );
(2) 对每条光谱流量归一化
选择4种不同类型的聚类方法挖掘不同的光谱形态特性, 分别基于划分的K-means、 基于模型的GMM(gaussian mixture model)、 谱聚类(spectral clustering)和层次聚类(agglomerative clustering)。 具体步骤如下:
(1) 初始化类别个数为6, 使用四种聚类算法对光谱数据进行聚类, 分别得到四个聚类结果c1、 c2、 c3、 c4。
(2) 采用匈牙利算法将c1、 c2、 c3、 c4的聚类标签对齐, 为每次聚类的结果赋予候选类标签(A、 B、 C、 D、 E、 F), 从而得到重构数据集S'。
(3) 由于没有先验知识, 假设满足4次聚类获取的候选类标签一致的情况, 分类可靠, 则属于6类的集合与相应类的下近似集相等。
(4) 选择投票数μ 的阈值为2, 获得6类上近似集为(1、 0.75、 0.5)三个可靠性梯度的类标签。
将6 626条光谱双星采用四种聚类方法分成6类, 分别为Type1— Type6, 然后对四组聚类结果进行投票决定每个样本的类别归属。
图2是四种聚类方法聚类结果的t-SNE可视化, 可以看出四种聚类算法的结果之间存在一定的差异, 而大致分布统一。 每个图中中间的数据分布较为密集, 周围存在一些稀疏的数据点, 稀疏的数据点是光谱中噪声过大或存在异常的样本。 通过投票的方法将所有数据分类结果划分为Ⅰ — Ⅳ 四个等级, 其中Ⅰ 等级是一致性最高的样本, 表示四种聚类结果都认定样本为某一个类别。
四种算法设定的聚类类别数为6, 其中GMM中协方差类型参数使用“ diag” , 即每个分量有各自不同对角协方差矩阵, SpectralClustering中“ affinity” 参数使用“ nearest_neighbors” , 邻居数量为20。
图3中为不同类别和不同投票数的样本数量, 绿色、 蓝色、 黄色分别表示投票数为4、 3、 2样本, 可以看出光谱双星中有大量的光谱通过不同聚类算法被划分到不同的类别中, 只有大约1/3的光谱在多个聚类算法下分类的结果相一致。 六类光谱中Type6的数量最少, 在图2中该类别是红色圆点表示, 可以看出其分布不集中, 大部分该类别的点在K-means、 AgglomerativeClustering、 GMM三个算法下的结果相同而SpectralClustering却将其划分到了其他的类别, 因此此类只有少量的高一致性光谱。
统计了不同类别和投票数的信噪比分布(r波段), 为了方便对比, 把大于50的当作50来统计, 结果如图4所示, 横轴是信噪比的大小, 纵轴是对应信噪比所占的比例。 可以看出Type4和Type5中有相对较多高信噪比的光谱, Type6中高信噪比光谱占比很少。 从最底部三个投票数的子图看, 投票数越少, 即聚类结果越不统一, 其高信噪比数量越少。
图5是四种聚类中2 186条可靠性为1的6类光谱均值谱和测光图像, 可以看出Type1类型光谱呈现的主导成分是蓝端吸收线特征, 而在红端呈现较弱的0红移Hα 发射线, 从测光图像上无明显双星特征, 因此推测这些目标光谱中混入较弱的河内星云发射线成分; Type2类型光谱呈现蓝端明显的吸收线特征, 而红端光谱质量比较低, 无法从连续谱或线的角度推测其类型, 而图像也未呈现明显的双星特征; Type3类型光谱呈现明显的M星特征, 图像也未呈现多星环境, 并未在已知双星星表中出现过, 因此这类双星疑似误判。 Type4— Type5类型光谱均呈现出明显的白矮星和M星双成分, 区别在于双星的亮度贡献不同; Type6呈现明显的星云发射线成分, 由图像上可以推测, 观测目标被星云成分导致了不同程度的遮挡。
 | 图5 可靠性为1的每类均值谱(a)和中心光谱对应图像与边界光谱对应图像(b)Fig.5 The mean spectra with reliability of 1 and the corresponding image of center spectrum (a) and (b) boundary spectrum for each type |
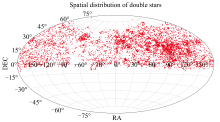
图6为光谱双星在天区中的分布, 可以看出来双星在天空中并非均匀分布, 在某些地方比如赤经95° 赤纬17° 附近是高密区域, 推测是由于该区域观测比例较高且光谱质量较低所导致[7]。
采用多种聚类方法投票的方法对LAMOST DR10发布的6 626条光谱进行了聚类分析, 首先找出复杂光谱数据中高一致性的样本, 即被多种类型的聚类方法都分为同一类的数据, 作为类别的代表样本, 然后根据低一致性样本的标签分配来分析其形态特点和与基础类别间的关系。 这种方法为复杂数据的类别划分提供了手段, 同时也能使研究者能够更加灵活地分析数据的形态特点。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|