改进粒子群优化算法结合BP神经网络模型的水体透射光谱总磷浓度预测研究

引用本文

张国浩, 王彩玲, 王洪伟, 于涛. 改进粒子群优化算法结合BP神经网络模型的水体透射光谱总磷浓度预测研究[J]. 光谱学与光谱分析, 2025,45(2): 394-402.
ZHANG Guo-hao, WANG Cai-ling, WANG Hong-wei, YU Tao. Improved Particle Swarm Optimization Algorithm Combined With BP Neural Network Model for Prediction of Total Phosphorus Concentration in Water Body Using Transmittance Spectral Data[J]. Spectroscopy and Spectral Analysis, 2025,45(2): 394-402.
Doi:10.3964/j.issn.1000-0593(2025)02-0394-09 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

改进粒子群优化算法结合BP神经网络模型的水体透射光谱总磷浓度预测研究

张国浩¹, 王彩玲^1,^*, 王洪伟^2,^*, 于涛³

1. 西安石油大学计算机学院, 陕西西安 710065

2. 西北工业大学光电与智能研究院, 陕西西安 710065

3. 中国科学院西安光学精密机械研究所, 陕西西安 710065

*通讯作者 e-mail: azering@163.com; wanghongwei@nwpu.edu.cn

作者简介: 张国浩, 2000年生,西安石油大学计算机学院硕士研究生 e-mail: zhangguohaogh@163.com

收稿日期: 2023-10-03 接受日期: 2024-06-17

基金: 陕西省重点研发计划项目(2023-YBSF-437),国家自然科学基金项目(61401439, 41301382, 31160475, 62002286, 62276213),中国科学院战略性先导科技专项(A类)(XDA23040101),西安石油大学研究生创新与实践能力培养项目(YCS23213173),西安石油大学研究生创新基金项目(YCX2412041)资助

摘要

使用光谱数据结合融合算法对水体污染物含量进行准确检测以保护水资源已成为一个关键问题。然而, 光谱数据的高维特性以及模型的不稳定常常导致预测效果不佳, 无法准确的进行检测。本研究提出了一种环保和准确的方法, 实现对长江水体中总磷浓度含量的预测。具体而言, 首先对测得的长江水质光谱数据进行最大最小归一化和均值中心化两种预处理操作, 在消除不同数据量级差异的同时去除了噪声, 确保了数据的一致性和可靠性。其次, 为了解决光谱数据的高维度问题, 采用了核主成分分析(KPCA)方法来降低数据维度并提取特征。 KPCA方法通过在高维度的空间中找到一个分类平面, 选出能代表原始数据99.42%信息量的前6个主成分, 用于后续预测模型的训练。接着在原始粒子群算法的基础上引入了粒子初始化规则、多种群竞争策略、参数自适应更新策略、种群多样性引导策略和粒子变异机制, 提高了粒子群的寻优能力, 降低粒子陷入局部最优解的概率。并使用改进后的粒子群算法对BP神经网络(BPNN)中的初始化权重和参数大小进行寻优, 从而加快网络的收敛效果, 提高预测能力。最后, 使用本研究所提出的预测模型对测试集中的样本进行总磷浓度的预测, 实验结果得到 R²为0.975 786, RMSE为0.002 242, MAE为0.001 612。将本模型与当前预测性能较好的其他基准模型进行预测效果的对比, 本研究所提出的模型对长江水体总磷浓度预测拟合效果更好, 精确度更高。在水资源保护和环境管理领域中使用光谱数据结合融合算法进行预测模型的研究和实践提供了新的思路和观点。

关键词: 光谱数据; 改进粒子群优化算法; BP神经网络模型; 核主成分分析(KPCA); 总磷浓度

中图分类号:O657.3 文献标志码:A

Improved Particle Swarm Optimization Algorithm Combined With BP Neural Network Model for Prediction of Total Phosphorus Concentration in Water Body Using Transmittance Spectral Data

ZHANG Guo-hao¹, WANG Cai-ling^1,^*, WANG Hong-wei^2,^*, YU Tao³

1. College of Computer Science, Xi'an Shiyou University, Xi'an 710065, China

2. School of Artificial Intelligence, Optics and Electronics, Northwestern Polytechnical University, Xi'an 710065, China

3. Xi'an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi'an 710065, China

*Corresponding authors

Abstract

The accurate detection of pollution levels in water bodies using transmission spectrum data and fusion algorithms has become crucial for safeguarding water resources. Inaccurate predictions and detection frequently result from the high-dimension of transmission spectrum data and model instability. The Yangtze River water body's total phosphorus concentration content is predicted in this study, and an accurate and environmentally friendly approach is suggested to achieve this goal. In particular, maxi-min normalization and mean-centering are two preprocessing operations carried out on the Yangtze River's measured water quality transmission spectrum data. These operations remove noise while eradicating differences between different data magnitudes, guaranteeing the consistency and reliability of the data. In addition, to solve the problem of the high dimension of the transmission spectrum data, the KPCA method is used to reduce the dimension of the data and extract the features. The KPCA method is used to select the top 6 principal components that represent 99.42% of the information content of the original data for subsequent prediction model training by finding a classification plane in a high-dimension space. Then, on the foundation of the initial particle swarm algorithm, the particle initialization rule, multiple swarm competition strategy, parameter adaptive update strategy, population diversity guidance strategy, and particle variation mechanism are added to improve the particle swarm's capacity for optimization and prevent particles from trapping in the local optimal solution. Additionally, the improved particle swarm algorithm optimizes the initialized weights and parameter values in the BP neural network to accelerate the convergence of the network and improve prediction performances. Finally, the total phosphorus content of the samples in the test set was predicted using the IMCPSO-BPNN model. The experimental results showed an R² of 0.975 786, an RMSE of 0.002 242, and an MAE of 0.001 612. The IMCPSO-BPNN model suggested in this work has a better fitting effect and better accuracy in forecasting the total nitrogen concentration in the Yangtze River water body when compared to other models such as the RF model, the BPNN model, and the PSO-BPNN model. It offers fresh concepts and viewpoints for studying and applying predictive modeling using transmission spectrum data and fusion algorithms to protect water resources and environmental management.

Keyword: Transmission spectrum; Improved particle swarm Optimization algorithm; BP Neural network; Kernel principal component analysis (KPCA); Total phosphorus concentration

文章图片

引言

随着当今社会的高速发展, 水污染问题日渐严重, 如何准确的对水体中污染物进行浓度的检测是治理和保护水资源绿色可持续发展的前提。长江作为我国的两大河流之一, 其水体质量直接关系到沿岸居民的健康和经济发展。因此, 加强长江水质监测, 对于保障居民用水安全、促进经济可持续发展具有重要意义。目前主要的检测方法有分光光度法, 化学发光发和色谱法等, 但这些检测方法存在检测周期长, 技术性要求高, 成本昂贵等缺点, 不能准确实时的对水体污染物进行检测^[1]。

光谱技术通过利用光谱仪获取水体的光谱信息, 并对其进行分析和处理, 可以快速、准确地识别水中的污染物, 并对其浓度进行定量分析, 已成为环境监测领域的重要技术手段之一^[2]。同时随着机器学习技术的不断发展, 使用光谱数据结合机器学习算法进行预测模型的构建已成为研究者们探讨的对象^{[3, 4]}。然而, 由于光谱数据具有的高维度特点, 以及大多数研究者只是简单地将机器学习算法移植到数据中, 导致模型训练效果较差, 缺乏对高维、算法精确度低等问题的有效处理。为此, 研究者们着重对降维技术和融合算法进行研究以改进预测精度。付玉等人使用改进的K-means降维方法, 首先用K-means算法分别在光谱空间和颜色空间将光谱数据聚类, 然后对每子类利用PCA法进行降维并重构, 为光谱降维提出了一种新的高效方法^[5]。杨峰针对目前算法图像自适应降维效果差、降维效率低的问题, 提出了PCA变换下的超光谱图像自适应降维算法, 得到了降维效果好和降维效率高的结果^[6]。针对传统降维算法处理后分类精度不高的问题, 董隽硕等人提出了一种双重L2, 1稀疏表示降维算法, 在强化特征的同时提高了低维数据的分类识别效果^[7]。李昌元等探究了线性降维方法与加入核函数的非线性降维方法间的差异, 实现了使用PCA和KPCA的高光谱遥感数据降维对比, 为研究者针对数据特点使用PCA或者KPCA方法提供了理论支撑^[8]。张沁宇等基于粒子群优化算法和反向传播神经网络两种算法, 通过实验对比分析构建了冷操草鱼新鲜鱼的近红外光谱预测模型, 能够很好的预测冷藏草鱼的新鲜度指标^[9]。胡劲华等使用连续小波变换和粒子群优化算法实现了光纤布拉格光栅传感网络的重叠光谱分类及调节, 有效降低了调解时间^[10]。杨样等探究了使用连续投影算法融合粒子群算法优化的BP神经网络(backpropagation neural network, BPNN)的分类监测模型, 对花生高光谱图像进行了分类性能和准确率的提升^[11]。

水中总磷的含量多少直接影响水体健康程度的评判, 对总磷含量的监测和控制是保障水体健康的重要措施之一^[12]。总磷是指水中各种形态磷的总和, 总磷含量过高会导致水体富营养化, 引发藻类过度生长、水生生物死亡等问题。在现有的研究报告中, 使用光谱数据结合融合算法模型对水体中总磷含量检测的报告较少。因此, 本实验重点对长江水体的光谱数据进行分析研究, 将光谱数据经过预处理操作后进行核主成分分析(kernel principal component analysis, KPCA)降维并选择合适的主成分个数, 之后使用改进的多种群竞争粒子群优化算法(improved multi-competitive particle swarm optimization, IMCPSO)与BP神经网络融合算法模型对长江中总磷的浓度进行预测。与三种基准预测模型对比, IMCPSO-BPNN模型预测效果最佳。

1 实验部分

1.1 样本收集

选择长江中湖北— 安徽地段作为研究区域, 该地段在长江流域具有重要的地理位置和环境意义。采样时间为2021年5月25日到2021年6月10日。在对选定的47个地点进行水质采集时, 每个地点在相同时间间隔下采集5次, 以确保样本的代表性和可靠性。通过这样的采集方式, 共获得了235个样本数据, 为后续的水质分析和评估提供数据基础。按照水质总磷测定的标准方法, 钼酸铵分光光度法, 进行溶液中总磷浓度的测量, 并且通过多次实验对比, 确保测量的相对误差在1.9%内。采集区域如图1所示。

	Figure Option View Download New Window
	图1 样本采集区域Fig.1 Sample collection area

1.2 光谱数据获取及预处理

针对长江的重要性和光谱技术的优势, 为了更好地了解水质特征, 首先使用光谱仪对采集到的样本进行光谱扫描。在本实验中, 我们使用透射光谱进行分析, 使用OCEAN-HDX-XR微型光纤光谱仪(美国Ocean Optics公司)采集长江样本的光谱数据, 该光谱仪具有高分辨率, 微型化和宽波长范围等特点。为实现监测目标, 拟采用微型光纤光谱仪结合紫外-可见吸收光谱分析法实现。实验平台的整体结构如图2所示, 主要由光纤光源、比色皿支架、比色皿、光纤光谱仪和计算机五部分组成。光源选用小型集成光纤氙灯光源HPX-2000(Ocean Optics公司出品)。在采集过程中对整个比色皿支架装置都进行了遮光处理, 从而进一步避免光照的干扰和保证采集环境稳定。测量开始前将光源预热15 min以上, 从而保证光源的稳定性。光源通过光纤提供入射光照射比色皿中的待测水样, 并经过光谱仪的分光与探测转变为电信号, 再经过光纤光谱仪的处理后上传至电脑端获得具体的光谱数据值。

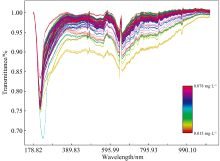
	Figure Option View Download New Window
	图2 水体光谱采集平台结构示意图 1: 光源; 2: 光纤; 3: 比色皿; 4: 支架; 5: 光纤光谱仪; 6: 计算机Fig.2 Schematic of the water spectra acquisition platform 1: Light source; 2: Optical fiber; 3: Cuvette; 4: Holder; 5: Fiber optic spectrometer; 6: Computer

为消除背景干扰, 测量了去离子水(纯水)的背景光谱, 将样本的光谱值与背景光谱值相除得到样本的光谱透射率大小, 该操作消除了背景光谱的影响, 从而获取样本光谱的相对强度信息。图3为样本的原始透射光谱图。

	Figure Option View Download New Window
	图3 原始光谱图Fig.3 Raw spectra

为了获得准确可靠的结果, 在对采集到的原始光谱数据进行进一步分析之前, 需要对数据进行预处理。预处理的目的是提高数据质量、去除噪声并使数据适合后续分析。通过观察可知, 测得的光谱数据中不存在明显的离群值。基于这个观察结果, 本实验采用了最大最小归一化和均值中心化两个预处理操作。这样做的目的是将数据缩放到统一的范围内, 消除了不同波段之间的量级差异, 确保各个波段对模型的影响相对均衡, 同时降低了噪声的影响并提高了数据的可解释性。

两种预处理操作有助于增强数据的相关性, 使得数据更适合后续分析。此外, 一些机器学习算法对数据的尺度比较敏感, 通过两种预处理方法可以提高算法的收敛速度, 加快计算过程。

通过预处理, 光谱数据的一致性和可靠性得到了保证, 并且减弱了噪声影响、减小了数据间的量级差异。这样的处理使得数据更适合后续的分析和建模, 提高了数据的一致性和可靠性。图4为进行最大最小归一化和均值中心化操作后的光谱数据图。

	Figure Option View Download New Window
	图4 预处理操作后光谱图Fig.4 Spectra after prepsocessing

1.3 数据降维

本实验测得数据的光谱范围为178.82~1 104.2 nm, 具有很高的维度。在这些特征中, 不仅存在不同特征对于模型的影响存在差异的情况, 而且特征之间还会相互进行影响。因此在处理高维度数据时, 需要考虑特征选择和降维技术以提取关键信息。特征选择的目标是选择对模型预测性能有重要贡献的特征, 而降维技术可以将高维数据转化为低维表示, 从而减少特征之间的冗余和噪声, 提高模型的拟合效果。

核主成分分析(KPCA)是在主成分分析方法基础上的拓展^{[13, 14]}。该方法通过使用核函数将原始数据映射到更高维度的空间中, 并在该空间找到一个线性可分的分类平面, 从而对原始数据进行降维和特征提取。

通过对光谱数据进行KPCA处理, 不仅能够降低数据维度、减少数据中的冗余信息和噪声, 还可以捕捉原始数据中的非线性关系^[14]。因为光谱特征通常具有复杂的非线性结构, 通过KPCA处理, 可以提取出更具表达力的非线性特征, 保持数据样本间的相对距离关系, 为后续的数据分析和建模提供更加有效和准确的数据表示。图5为使用KPCA后所对应方差解释率最大的前十五个主成分以及累积方差。通过观察图5可知, 第一个和第二个主成分所含有的信息量最高, 分别为0.631 0和0.227 0。这意味着前两个主成分能够包含原始数据中大部分的信息, 具有很高的重要性, 可以视为与原始数据最相关的特征; 第三个及之后的主成分所含有的信息量均低于0.1, 表示这些主成分能够解释原始数据中较少的信息。为了模型训练时的准确性和稳定性, 选择能够代表原始数据99.42%信息量的前六个主成分来进行后续实验模型中的训练。

	Figure Option View Download New Window
	图5 主成分方差解释率和累积方差值Fig.5 Principal component variance explained and cumulative variance values

1.4 改进的多种群竞争粒子群优化算法

粒子群优化(particle swarm optimization, PSO)算法是一种模拟鸟类觅食行为的群体智能优化算法, 通过模拟粒子在解空间中的移动和信息交流来寻找最优解。作为一种常见的优化算法, PSO算法通常适用于连续优化问题, 并具有较好的全局搜索和收敛性能^[15]。 PSO算法的核心思想是粒子之间相互的合作和信息交流, 通过不断更新粒子的速度和位置来逐步靠近全局最优解。在寻优过程中, 每个粒子代表一个解, 在搜索过程中通过与其他粒子的交互, 通过自身的个体和群体经验进行位置的调整, 这种合作与信息交流的机制使得粒子能够共同探索解空间, 并逐渐找到更优的解^[16]。然而, PSO算法却存在收敛速度不稳定、粒子在搜索过程中容易陷入局部最优解等问题。为了进一步提升算法的性能, 在原始算法的基础上引入了多种优化策略, 在加快算法收敛速度的同时, 尽可能解决原始算法的不足。图6为改进粒子群算法的优化策略示意图。

	Figure Option View Download New Window
	图6 改进粒子群算法优化策略示意图Fig.6 The improved particle swarm optimization strategy diagram

1.4.1 粒子初始化规则

原始PSO算法在进行群体粒子速度和位置的初始化时, 由于没有先验知识, 通常采用随机生成的方式, 在搜索空间范围来确定初始位置。该方式虽然具有随机性, 但是却也存在可能会导致粒子分布不均匀、收敛时间较长等缺陷, 这些缺陷会导致粒子群体不能很好的在搜索空间中进行探索。为了解决这一问题, 使用Logistic映射对粒子群中的速度和位置进行初始化^[17]。 Logistic映射是一种常见的非线性映射函数, 常用于生成混沌序列, 通过不断的迭代递推, 产生介于0和1之间的随机数序列。该映射的公式如式(1)所示。

$X_{n + 1} = r X_{n} (1 - X_{n})$ (1)

式(1)中, X_n为第n次迭代值, X_n₊₁表示第n+1次迭代值, r为控制参数, 通常取值在0~4之间。

通过使用Logistic映射来初始化粒子群中的速度和位置, 可以引入混沌性和随机性, 增加粒子的多样性, 有助于更好地探索解空间。这种初始化方法可以提供一定的随机性, 同时也有助于加速算法的收敛过程, 改善算法的全局搜索能力。

1.4.2 多种群竞争策略

在粒子速度和位置初始化设置完成后, 为了进一步提升粒子群的搜索性能和寻优能力, 在原有粒子群算法的基础上引入了多种群竞争策略。首先, 将整个种群划分为一个主种群和两个从种群。其次, 在两个从种群之间引入了竞争策略。该策略通过从种群之间的竞争机制和主从种群间的相互合作和影响来增强算法的寻优能力^{[18, 19, 20]}。

当粒子群进行寻优时, 两个从种群之间通过竞争策略选出从种群局部最优粒子; 主种群中根据适应度值的大小选择出主种群局部最优粒子。此时粒子群中的所有粒子在进行速度更新时会受到自身历史最优解、从种群局部最优解、主种群局部最优解和全局最优解四个优秀粒子的影响, 从而更好探索解空间。通过该策略, 不仅能让粒子朝着种群中优秀粒子的方向移动, 而且由于多个优秀粒子共同影响速度更新, 能够极大程度上避免陷入局部最优解^[21]。

两个从种群内部的粒子在竞争策略下通过计算竞争度和牺牲度的大小来选择出从种群局部最优粒子。竞争度和牺牲度是根据自然界中生物的竞争关系所提出的概念, 用于评估两个从种群中粒子能力的强弱。在两个从种群中, 其中一个作为捕食者(H)种群, 使用竞争度值代表粒子的优劣程度; 另外一个为被捕食者(F)种群, 使用牺牲度值大小代表粒子的优劣程度。在竞争过程中, 首先计算F种群中牺牲度值的大小, 后根据F种群计算H种群中每个粒子的竞争度值, 最后在H种群中选出从种群局部最优粒子。使用均方根误差(RMSE)作为例子适应度之评估的结果。两个种群中竞争度和牺牲度的计算公式如式(2)、式(3)所示。

$B (i) = \sum_{f (p) f (i)} \frac{1}{len (P)}, \forall p \in P, i \in H$ (2)

$C (j) = \sum_{f (j) f (h)} B (h) f (h), j \in P, \forall h \in H$ (3)

式(2)和式(3)中, f(h)代表粒子h的适应度值, len(P)为P种群中的粒子个数; B(i)为H种群中粒子i的牺牲度值; C(j)代表P种群中粒子j的竞争度, C(j)的大小为在H种群中小于粒子j适应度值的所有粒子的牺牲度和对应适应度值的乘积之和。

在粒子速度更新的过程中会受到多个最优粒子的共同影响, 为了让粒子朝着更优的方向移动, 对于从种群局部最优粒子和主种群局部最优粒子, 提出自适应权重影响因子概念。该影响因子的函义是通过根据粒子的表现和搜索进展, 自适应的调整从种群局部最优粒子和主种群局部最优粒子在速度更新公式中的权重大小从而影响粒子的行为。自适应权重影响因子的计算公式如式(4)、式(5)所示。

$k = sigmoid (f (Gbest_subord) - f (Gbest_main))$ (4)

$sigmoid (x) = \frac{1}{1 + e^{- x}}$ (5)

式(4)和式(5)中, f(Gbest_subord)和f(Gbest_main)分别代表从种群局部最优粒子和主种群局部最优粒子的适应度值。

在原始粒子群算法中, 每个粒子的更新只受到自身历史最优解和全局最优粒子的影响, 这意味着只有个体学习因子和社会学习因子两个参数起作用。然而, 为了增加算法的多样性和搜索能力, 在社会学习因子的基础上提出了全局社会学习因子和局部社会学习因子的概念, 进一步扩展了参数的作用。粒子群中粒子的速度更新公式如式(6)所示。

$\begin{array}{l} V_{i}^{d + 1} = ω V_{i}^{d} + c_{1} r_{1} (Pbes t_{i}^{d} - x_{i}^{d}) + k c_{2} r_{2} (Gbes t_{main}^{d} - x_{i}^{d}) + \\ (1 - k) c_{2} r_{2} (Gbes t_{subord}^{d} - x_{i}^{d}) + c_{3} r_{3} (Gbes t^{d} - x_{i}^{d}) \end{array}$ (6)

式(6)中, Pbes $t_{i}^{d}$ 是粒子i的历史最优解, Gbest^d是粒子群的全局最优解, Gbes ${t^{d}}_{main}$ 是主种群局部最优解, Gbes ${t^{d}}_{subord}$ 是从种群局部最优解, ω 为惯性权重, c₁、 c₂、 c₃分别为个体学习因子、局部社会学习因子和全局社会学习因子, r₁、 r₂、 r₃为0~1范围内的随机数, k为权重影响因子。

粒子群中每个粒子的位置更新公式如式(7)所示。

$x_{i}^{d + 1} = x_{i}^{d} + V_{i}^{d + 1}$ (7)

为了使从种群中所有粒子能够共同影响和相互进化, 在每次迭代后P种群和F种群中的粒子都会进行互换, 从而让两个种群中所有粒子都变得更加优秀, 加快算法的收敛速度。

1.4.3 参数更新策略

在传统的粒子群算法中, 惯性权重、个体学习因子和社会学习因子通常为固定的常数, 参数值过大或过小都会导致寻优结果不稳定, 收敛效果差的缺点^[22]。为了提高粒子速度更新的效果和加快收敛速度, 使用参数自适应更新策略动态地调整惯性权重、个体学习因子、局部社会学习因子和全局社会学习因子, 使其能够适应问题的变化, 并在搜索过程中进行优化^{[22, 23]}。

参数更新策略是根据当前粒子的适应度值以及粒子群中所有粒子的平均适应度值之间的大小来进行判断。如果当前粒子的适应度值大于平均适应度值, 表明粒子距离最优解较远, 此时应增大个体学习因子, 减少局部社会学习因子、全局社会学习因子和惯性权重的值, 让粒子更好的在解空间中进行探索; 当粒子的适应度值小于平均适应度值时, 表明粒子距离最优解较近, 此时应减少个体学习因子, 增大局部社会学习因子、全局社会学习因子和惯性权重的值, 让粒子更好的收敛于最优解; 同时, 为了在粒子群算法的迭代过程中, 在前期增加探索性能, 而在后期加快收敛性能, 在参数的更新公式中引入控制变量z, 动态的根据迭代过程控制参数的更新尺度。控制变量z的计算公式如式(8)所示。

$z = 1 - \frac{t}{T}$ (8)

式(8)中, t为当前迭代次数, T为总迭代次数。

式(9)— 式(13)为个体社会学习因子、局部社会学习因子、全局社会学习因子和惯性权重的更新公式。

$c_{1} = c_{1} + m_{2} z (c_{1_{\max}} - c_{1_{\min}} softsign (\frac{f_{i} - f_{avg}}{f_{avg} - f_{\min}})$ (9)

$c_{2} = c_{2} - m_{3} z (c_{2_{\max}} - c_{2_{\min}}) softsign (\frac{f_{i} - f_{avg}}{f_{avg} - f_{\min}})$ (10)

$c_{3} = c_{3} - m_{4} z (c_{3_{\max}} - c_{3_{\min}}) softsign (\frac{f_{i} - f_{avg}}{f_{avg} - f_{\min}})$ (11)

$ω = ω - m_{1} z (ω_{\max} - ω_{\min}) softsign (\frac{f_{i} - f_{avg}}{f_{avg} - f_{\min}})$ (12)

$softsign (x) = \frac{x}{1 + |x|}$ (13)

式(9)— 式(13)中, ω _max、 ω _min、 $c_{1_{\max}}$ 、 $c_{1_{\min}}$ 、 $c_{2_{\max}}$ 、 $c_{2_{\min}}$ 、 $c_{3_{\max}}$ 和 $c_{3_{\min}}$ 表示惯性权重ω 、个体学习因子c₁、局部社会学习因子c₂和全局社会学习因子c₃的最大值和最小值, f_i表示当前粒子的函数适应值, f_min表示粒子群体中最小的函数适应值, 相当于此时粒子群中的全局最优粒子, f_avg表示粒子群中的所有粒子的平均适应值, m₁、 m₂、 m₃和m₄为0~1范围内的随机数, z为控制变量。

1.4.4 种群多样性引导策略

在粒子群算法中, 当粒子群体集中分布在某个局部区域时, 可能会导致种群的多样性值较低, 使得算法难以跳出局部最优解。为了解决这个问题, 引入了粒子种群多样性引导策略, 通过多样性值的大小选择适当的粒子速度更新方式^[24]。

该策略每次迭代过程中都会计算种群中粒子的多样性值, 计算公式如式(14)所示。较高的多样性值代表粒子群体在解空间中分布比较发散, 此时虽然能较好的对空间中的区域进行探索, 但不利于粒子收敛; 较低的多样性值代表粒子群体在解空间中分布比较集中, 此时虽然有利于群体收敛, 但可能会陷入局部最优解, 不能很好的探索其他的空间以发现更优解。

$D (X_{n}) = \frac{1}{Nd} \sum_{i = 1}^{N} | x_{i, n} - {\bar{x}}_{n} |$ (14)

式(14)中, N为种群中的粒子个数, d为搜索空间的对角线长度, 代表搜索区域的大小, ${\bar{x}}_{n}$ 为所有粒子的平均位置。

通过计算粒子群体中的多样性大小, 并根据多样性上界d_high和多样性下界d_low选择合适的速度更新方式。当多样性值小于d_low时, 表示粒子群体的分布过于集中, 不利于探索其他空间。此时粒子应采取更具探索性的速度更新方式, 以帮助粒子群体跳出局部最优解, 增加对解空间的探索; 当多样性值大于d_high时, 表示粒子群体的分布过于分散, 不利于群体的收敛性。此时粒子应采取较更具收敛性的速度更新方式, 以加快收敛速度; 当多样性值大于d_low且小于d_high时, 表示粒子群体的多样性在一个合理的范围内, 既不过于集中也不过于分散。此时粒子会受到自身历史最优解的吸引但会被全局和局部最优粒子所排斥, 以更好的进行收敛和探索。该策略下粒子的速度更新公式如式(15)所示。

$\begin{array}{l} V_{i}^{d + 1} = \\ \{\begin{array}{l} ω V_{i}^{d} + c_{1} r_{1} (Pbes t_{i}^{d} - x_{i}^{d}) + k c_{2} r_{2} (Gbes t_{main}^{d} - x_{i}^{d}) + (1 - k) c_{2} r_{2} (Gbes t_{subord}^{d} - x_{i}^{d}) + c_{3} r_{3} (Gbes t^{d} - x_{i}^{d}) & D (X_{n}) d_{high} \\ ω V_{i}^{d} + c_{1} r_{1} (Pbes t_{i}^{d} - x_{i}^{d}) - k c_{2} r_{2} (Gbes t_{main}^{d} - x_{i}^{d}) - (1 - k) c_{2} r_{2} (Gbes t_{subord}^{d} - x_{i}^{d}) - c_{3} r_{3} (Gbes t^{d} - x_{i}^{d}) & otherwise \\ ω V_{i}^{d} - c_{1} r_{1} (Pbes t_{i}^{d} - x_{i}^{d}) - k c_{2} r_{2} (Gbes t_{main}^{d} - x_{i}^{d}) - (1 - k) c_{2} r_{2} (Gbes t_{subord}^{d} - x_{i}^{d}) - c_{3} r_{3} (Gbes t^{d} - x_{i}^{d}) & D (X_{n}) d_{low} \end{array} \end{array}$
(15)

式(15)中, Pbes $t_{i}^{d}$ 为粒子i在第d次迭代时的历史最优位置, Gbes ${t^{d}}_{subord}$ 为第d次迭代时的从种群最优粒子, Gbes ${t^{d}}_{main}$ 为第d次迭代时的主种群最优粒子, Gbest^d第d次迭代时的全局最优粒子, ω 为惯性权重, c₁、 c₂、 c₃分别为个体学习因子、局部社会学习因子和全局社会学习因子, k为影响因子, r₁、 r₂、 r₃为0~1内的随机数。

1.4.5 粒子变异机制

通过引入粒子初始化规则、多种群竞争策略、参数更新规则以及种群多样性引导策略, 增强了算法的寻优能力, 使粒子在解空间中更好地进行全局搜索。同时, 为了进一步提升算法的性能, 降低粒子陷入局部最优解的风险, 在遗传算法和模拟退火算法的基础上提出了粒子的变异机制, 以增强群体中粒子的随机性和探索能力。该机制在每次迭代完成后都会循环遍历群体中的每个粒子, 并根据变异规则判断是否对粒子进行变异^{[16, 25]}。

对于群体中的每个粒子, 首先使用式(8)中的控制变量参数z来控制扰动因子e的大小, 以达到在迭代前期扰动因子e较大, 迭代后期扰动因子e较小的目的, 计算公式如式(16)所示; 之后, 使用扰动因子对粒子当前位置的每个维度进行扰动后得到扰动向量c, 并将扰动向量c与粒子当前位置相加得到粒子的变异位置。扰动向量c以及粒子新位置的计算如式(17)、式(18)所示; 最后, 使用变异规则来判断粒子是否进行变异操作。具体的判断规则为: 使用变异粒子的适应度值减去原始粒子的适应度值, 根据该差值的大小和生成0~1内的随机数两个条件来判断粒子是否进行变异。当差值小于0时, 表明变异粒子比原始粒子更优, 此时进行变异操作; 当差值大于0时, 表明原始粒子较优, 此时根据随机数大小来判断是否进行变异。如果随机数小于0.1, 则进行变异操作, 否则便不进行变异, 以增加粒子的随机性和多样性。

$e = zr$ (16)

式(16)中, z为控制变量, r为-1~1区间内的随机数。

$c = eX (i)$ (17)

$P_new (i) = P (i) + c$ (18)

式(17)和式(18)中, c为扰动向量, e为扰动因子, P(i)为粒子i的当前位置, P_{_}ew(i)为使用扰动因子对粒子i进行扰动后的变异位置。

1.5 BP神经网络(BPNN)

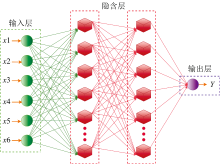
BPNN是一种应用十分广泛的人工神经网络模型, 用于解决监督学习问题, 特别是在分类和回归任务中有着广泛应用, 由输入层、隐含层和输出层三部分组成。每个神经元与前一层的所有神经元相互连接, 并且具有权重和偏置。该神经网络的训练过程分为前向传播和反向传播两部分, 在前向传播时神经网络中的信号传递是从输入层到输出层的, 通过计算每个神经元的加权和, 然后通过激活函数进行非线性变换。反向传播时基于梯度下降优化策略, 通过迭代地计算输出与目标之间的误差, 并根据误差值调整网络中的权重和偏置大小, 以最小化误差。图7为神经网络的结构示意图。

	Figure Option View Download New Window
	图7 神经网络结构示意图Fig.7 Schematic diagram of neural network structure

BPNN的关键优势之一是它可以通过大量的训练样本来学习复杂的非线性特征和模式, 在一定程度上具有容错性。然后, BPNN也存在一些挑战和注意事项。首先, 在初始化神经网络的权重和偏置时, 由于缺乏先验知识, 通常采用随机生成的方式, 这可能会对网络的训练和收敛产生影响。其次, 神经网络的性能会受到网络结构和学习率的影响, 参数的不同选择会对神经网络的性能造成影响。因此在BPNN进行训练前, 首先使用本实验所提出的改进的多种群竞争策略粒子群优化算法对BPNN中的初始化权重和偏置组合进行寻优, 通过该方式能够提高网络的初始性能以及训练时的收敛速度, 从而改善模型的性能。同时对神经网络中的学习率参数进行了自适应改进, 让其动态的进行调整, 进一步优化网络的训练过程。

1.5.1 学习率自适应调整策略

神经网络中的学习率参数用于指定更新权重和偏置时的步长大小, 通常是一个固定的常数。过大的学习率会导致训练不稳定, 而过小的学习率则会导致收敛速度缓慢。为解决这一问题, 提出了学习率自适应调整策略, 利用sigmoid函数非线性的特点并结合损失函数的变化值, 使学习率根据当前神经网络的训练效果动态地调整学习率参数^[26]。式(19)为学习率自适应公式。

$r = r [1.5 - sigmoid (f_{t} - f_{t - 1})]$ (19)

式(19)中, r为学习率, f_t-f_t_-1表示t时刻与上一时刻损失函数的变化值。

2 结果与讨论

2.1 基于IMCPSO-BPNN模型算法的实验

2.1.1 BPNN内部激活函数选择

选择适当的激活函数对于BP神经网络的预测性能具有重要影响。常见的激活函数如Sigmoid、 ReLU和Tanh等, 它们在模型学习和表示数据的非线性关系方面发挥着重要作用。然而, 不同的问题和数据集规模需要不同的激活函数来获得最佳效果。

为了进一步提升BP神经网络预测性能和表现, 我们使用不同的激活函数利用相同的数据集进行了对比实验从而找到最适合的激活函数。不同激活函数下BP神经网络的表现性能如表1所示。

表1 不同激活函数下BP神经网络的表现性能 Table 1 Performance of BP neural network under different activation functions

通过表1可知, BP神经网络使用Sigmoid激活函数时模型表现性能最佳。相比ReLU以及Tanh激活函数, 使用Sigmoid时R²提升了48.7%, 71.45%, RMSE降低了50.41%, 71.23%, MAE降低了44.15%, 45.92%。因此本研究选择使用Sigmoid作为BP神经网络的激活函数, 以获得最佳效果。

2.1.2 模型预测

首先使用IMCPSO对BPNN的初始化权重和偏置组合进行寻优, 以提高神经网络模型的初始性能和训练速度。之后使用学习率自适应条件下的BPNN对长江水质光谱数据中的总磷浓度进行预测。训练模型时, 分别将样本数据按照7∶ 3、 8∶ 2、 9∶ 1划分为训练集和测试集, 使用留一交叉验证法进行模型的训练和调优, 并使用测试集进行模型效果的验证。三种不同划分方式测试集中模型的预测结果如图8所示。

	Figure Option View Download New Window
	图8 不同划分方式下IMCPSO-BPNN模型预测结果Fig.8 IMCPSO-BPNN model prediction results under different partitioning methods

为了评价模型的性能, 分别使用决定系数R², 均方根误差RMSE和平均绝对误差MAE对模型的预测精度进行了分析。三个评估参数值在三种不同划分规则下的结果如表2所示。通过对图7以及对表2中三个评估参数值的观察, 说明本模型对于水体总磷的浓度预测具有很好的效果。

表2 不同划分方式下的模型性能对比 Table 2 Comparison of model performance between different partitioning methods

2.2 模型结果分析

将IMCPSO-BPNN模型与随机森林(random forest, RF)模型、 BPNN模型和粒子群优化下的BPNN(PSO-BPNN)模型进行预测效果的对比, 观察本实验所提出的模型在性能上是否有所增强。对比结果如表3所示。

表3 模型预测性能对比 Table 3 Comparison of model prediction performance

通过表3可以清晰地看出IMCPSO-BPNN预测模型在总磷浓度预测方面相较于其他模型表现出更佳的性能。这表明该模型能够准确地捕捉长江水体总磷浓度的变化趋势, 并提供更可靠的预测结果。

3 结论

针对光谱数据的高维特性以及建立模型的不稳定性常常导致预测效果不佳情况, 以长江中湖北— 安徽地段的47个地点作为研究区域, 基于所测得的光谱数据建立了IMCPSO-BP预测模型, 对总磷浓度进行分析预测。结论如下:

(1)通过最大最小归一化和均值中心化两种预处理操作, 降低了噪声的干扰, 消除了光谱数据之间的差异, 使数据更加稳定和一致, 提高了后续模型的拟合效果。

(2)使用KPCA对长江光谱数据进行降维和特征提取, 从原始数据中提取具有重要信息特征的同时降低了数据的维度, 提高了数据的可处理性和可解释性。

(3)使用IMCPSO算法对神经网络初始化和权重和偏置组合进行寻优, 提高神经网络的拟合收敛效果。通过在粒子群算法的基础上引入了多种群竞争规则和参数自适应更新策略等多种优化策略, 提高了粒子群的寻优能力, 减低了种群中粒子陷入局部最优解的概率。

(4)使用提出的IMCPSO-BP算法融合模型对长江测试集数据进行总磷浓度的预测, 预测准确性较高, 其反演效果也明显好于其他模型。为使用光谱数据结合融合算法对长江中水质的检测和管理提供新的方法和科学依据。

(5)使用IMCPSO优化BP神经网络的初始化权重和偏置, 达到了较好的优化效果。但BP神经网络中涉及的关键参数较多, 因此在未来的研究中将着重探索优化算法优化BP神经网络下多个关键参数的可行性和效果, 进一步提高研究质量。

参考文献

文献列表

[1]	WANG Cai-ling, WANG Bo, JI Tong, et al(王彩玲, 王波, 纪童, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(7): 2181. [本文引用:1]
[2]	FENG Tian-shi, PANG Zhi-guo, JIANG Wei, et al(冯天时, 庞治国, 江威, 等). Journal of Geo-information Science(地球信息科学学报), 2021, 23(9): 1646. [本文引用:1]
[3]	HUANG Hua, LI Mao-yi, CHEN Yin-hui, et al(黄华, 李茂亿, 陈吟晖, 等). Water Resources Protection(水资源保护), 2021, 37(5): 36. [本文引用:1]
[4]	CHEN Jun-ying, XING Zheng, ZHANG Zhi-tao, et al(陈俊英, 邢正, 张智韬, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2019, 50(11): 200. [本文引用:1]
[5]	FU Yu, WAN Xiao-xia, LIU Zhi-hong, et al(付玉, 万晓霞, 刘志宏, 等). Printing and Digital Media Technology Study(印刷与数字媒体技术研究), 2023, (2): 22. [本文引用:1]
[6]	YANG Feng(杨峰). Computer Simulation(计算机仿真), 2019, 36(8): 435. [本文引用:1]
[7]	DONG Jun-shuo, WU Ling-da(董隽硕, 吴玲达). Computer Engineering and Design(计算机工程与设计), 2023, 44(4): 1122. [本文引用:1]
[8]	LI Chang-yuan, LIU Guo-dong, TAN Bo(李昌元, 刘国栋, 谭博). Geospatial Information(地理空间信息), 2022, 20(7): 89. [本文引用:1]
[9]	ZHANG Qin-yu, HU Zhi-gang, XU Zi-jian, et al(张沁宇, 胡志刚, 徐子健, 等). Journal of Food Safety & Quality(食品安全质量检测学报), 2023, 14(22): 200. [本文引用:1]
[10]	HU Jin-hua, ZHENG Bing-li, DENG Yu-jing, et al(胡劲华, 郑炳理, 邓玉静, 等). Laser & Optoelectronics Progress(激光与光电子学进展), 2023, 60(21): 149. [本文引用:1]
[11]	YANG Yang, XU Xi-ping, XUE Hang, et al(杨洋, 徐熙平, 薛航, 等). Laser Technology(激光技术), 2024, 48(4): 556. [本文引用:1]
[12]	SUN Wei, ZHU Ying, LI Chang-xiu, et al(孙巍, 朱颖, 李长秀, 等). Environmental Pollution & Control(环境污染与防治), 2022, 44(12): 1628. [本文引用:1]
[13]	LIN Nan, LIU Han-lin, MENG Xiang-fa, et al(林楠, 刘翰霖, 孟祥发, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2021, 52(3): 218. [本文引用:1]
[14]	XU Han-qiu, LI Chun-qiang, LIN Meng-jing(徐涵秋, 李春强, 林梦婧). Geomatics and Information Science of Wuhan University[武汉大学学报(信息科学版)], 2023, 48(4): 506. [本文引用:2]
[15]	DUAN Yi-fan, LIU Xiao-jie, LI Xin, et al(段一凡, 刘小杰, 李欣, 等). China Metallurgy(中国冶金), 2023, 33(11): 114. [本文引用:1]
[16]	KANG Yan-song, ZANG Shun-lai(康岩松, 臧顺来). Journal of Northeastern University(Natural Science)[东北大学学报(自然科学版)], 2023, 44(8): 1089. [本文引用:2]
[17]	LIU Gong-zhi, WU Qiong, WANG Guang-yi, et al(刘公致, 吴琼, 王光义, 等). Journal of Electronics & Information Technology(电子与信息学报), 2022, 44(10): 3602. [本文引用:1]
[18]	WANG Zhen-dao, ZHANG Yi-ming, SHI Xue-qian(王镇道, 张一鸣, 石雪倩). Journal of Hunan University(Natural Sciences)[湖南大学学报(自然科学版)], 2021, 48(6): 80. [本文引用:1]
[19]	ZHANG Hu, ZHANG Heng, HUANG Zi-lu, et al(张虎, 张衡, 黄子路, 等). Journal of System Simulation(系统仿真学报), 2024, 36(4): 844. [本文引用:1]
[20]	GUAN Ren-chu, HE Bao-run, LIANG Yan-chun, et al(管仁初, 贺宝润, 梁艳春, 等). Journal of Jilin University(Engineering and Technology Edition)[吉林大学学报(工学版)], 2022, 52(8): 1842. [本文引用:1]
[21]	LI Wei, DING Shu-hui, CHEN Xun-jun(李伟, 丁书慧, 陈勋俊). Application Research of Computers(计算机应用研究), 2023, 40(11): 3254. [本文引用:1]
[22]	WEI Hai-bin, WEI Dong-sheng, JIANG Bo-yu, et al(魏海斌, 魏东升, 蒋博宇, 等). Journal of South China University of Technology(Natural Science Edition)[华南理工大学学报(自然科学版)], 2023, 51(6): 62. [本文引用:2]
[23]	SHI Jing-can, TANG Shou-feng, ZHAO Zhi-wei, et al(史经灿, 唐守锋, 赵志伟, 等). Transducer and Microsystem Technologies(传感器与微系统), 2023, 42(7): 70. [本文引用:1]
[24]	CHENG Mei-ying, QIAN Qian, NI Zhi-wei(程美英, 钱乾, 倪志伟). Control and Decision(控制与决策), 2024, 39(3): 728. [本文引用:1]
[25]	WANG Kun, HOU Shu-xian, WANG Li(王坤, 侯树贤, 王力). Systems Engineering and Electronics(系统工程与电子技术), 2021, 43(2): 526. [本文引用:1]
[26]	SONG Yu-cun, GE Quan-bo, ZHU Jun-long, et al(宋玉存, 葛泉波, 朱军龙, 等). Acta Aeronautica et Astronautica Sinica(航空学报), 2023, 44(14): 327951. [本文引用:1]

2022

0.0

... 目前主要的检测方法有分光光度法, 化学发光发和色谱法等, 但这些检测方法存在检测周期长, 技术性要求高, 成本昂贵等缺点, 不能准确实时的对水体污染物进行检测^[1] ...

2021

0.0

... 光谱技术通过利用光谱仪获取水体的光谱信息, 并对其进行分析和处理, 可以快速、准确地识别水中的污染物, 并对其浓度进行定量分析, 已成为环境监测领域的重要技术手段之一^[2] ...

2021

0.0

... 同时随着机器学习技术的不断发展, 使用光谱数据结合机器学习算法进行预测模型的构建已成为研究者们探讨的对象^[3,4] ...

2019

0.0

... 同时随着机器学习技术的不断发展, 使用光谱数据结合机器学习算法进行预测模型的构建已成为研究者们探讨的对象^[3,4] ...

2023

0.0

... 付玉等人使用改进的K-means降维方法, 首先用K-means算法分别在光谱空间和颜色空间将光谱数据聚类, 然后对每子类利用PCA法进行降维并重构, 为光谱降维提出了一种新的高效方法^[5] ...

2019

0.0

... 杨峰针对目前算法图像自适应降维效果差、降维效率低的问题, 提出了PCA变换下的超光谱图像自适应降维算法, 得到了降维效果好和降维效率高的结果^[6] ...

2023

0.0

... 针对传统降维算法处理后分类精度不高的问题, 董隽硕等人提出了一种双重L2, 1稀疏表示降维算法, 在强化特征的同时提高了低维数据的分类识别效果^[7] ...

2022

0.0

... 李昌元等探究了线性降维方法与加入核函数的非线性降维方法间的差异, 实现了使用PCA和KPCA的高光谱遥感数据降维对比, 为研究者针对数据特点使用PCA或者KPCA方法提供了理论支撑^[8] ...

2023

0.0

... 张沁宇等基于粒子群优化算法和反向传播神经网络两种算法, 通过实验对比分析构建了冷操草鱼新鲜鱼的近红外光谱预测模型, 能够很好的预测冷藏草鱼的新鲜度指标^[9] ...

2023

0.0

... 胡劲华等使用连续小波变换和粒子群优化算法实现了光纤布拉格光栅传感网络的重叠光谱分类及调节, 有效降低了调解时间^[10] ...

2024

0.0

... 杨样等探究了使用连续投影算法融合粒子群算法优化的BP神经网络(backpropagation neural network, BPNN)的分类监测模型, 对花生高光谱图像进行了分类性能和准确率的提升^[11] ...

2022

0.0

... 水中总磷的含量多少直接影响水体健康程度的评判, 对总磷含量的监测和控制是保障水体健康的重要措施之一^[12] ...

2021

0.0

... 核主成分分析(KPCA)是在主成分分析方法基础上的拓展^[13,14] ...

2023

0.0

... 核主成分分析(KPCA)是在主成分分析方法基础上的拓展^[13,14] ...

... 通过对光谱数据进行KPCA处理, 不仅能够降低数据维度、减少数据中的冗余信息和噪声, 还可以捕捉原始数据中的非线性关系^[14] ...

2023

0.0

... 作为一种常见的优化算法, PSO算法通常适用于连续优化问题, 并具有较好的全局搜索和收敛性能^[15] ...

2023

0.0

... 在寻优过程中, 每个粒子代表一个解, 在搜索过程中通过与其他粒子的交互, 通过自身的个体和群体经验进行位置的调整, 这种合作与信息交流的机制使得粒子能够共同探索解空间, 并逐渐找到更优的解^[16] ...

... 该机制在每次迭代完成后都会循环遍历群体中的每个粒子, 并根据变异规则判断是否对粒子进行变异^[16,25] ...

2022

0.0

... 为了解决这一问题, 使用Logistic映射对粒子群中的速度和位置进行初始化^[17] ...

2021

0.0

... 该策略通过从种群之间的竞争机制和主从种群间的相互合作和影响来增强算法的寻优能力^[18,19,20] ...

2024

0.0

... 该策略通过从种群之间的竞争机制和主从种群间的相互合作和影响来增强算法的寻优能力^[18,19,20] ...

2022

0.0

... 该策略通过从种群之间的竞争机制和主从种群间的相互合作和影响来增强算法的寻优能力^[18,19,20] ...

2023

0.0

... 通过该策略, 不仅能让粒子朝着种群中优秀粒子的方向移动, 而且由于多个优秀粒子共同影响速度更新, 能够极大程度上避免陷入局部最优解^[21] ...

2023

0.0

... 在传统的粒子群算法中, 惯性权重、个体学习因子和社会学习因子通常为固定的常数, 参数值过大或过小都会导致寻优结果不稳定, 收敛效果差的缺点^[22] ...

... 为了提高粒子速度更新的效果和加快收敛速度, 使用参数自适应更新策略动态地调整惯性权重、个体学习因子、局部社会学习因子和全局社会学习因子, 使其能够适应问题的变化, 并在搜索过程中进行优化^[22,23] ...

2023

0.0

2024

0.0

... 为了解决这个问题, 引入了粒子种群多样性引导策略, 通过多样性值的大小选择适当的粒子速度更新方式^[24] ...

2021

0.0

... 该机制在每次迭代完成后都会循环遍历群体中的每个粒子, 并根据变异规则判断是否对粒子进行变异^[16,25] ...

2023

0.0

... 为解决这一问题, 提出了学习率自适应调整策略, 利用sigmoid函数非线性的特点并结合损失函数的变化值, 使学习率根据当前神经网络的训练效果动态地调整学习率参数^[26] ...