基于中国传统岩彩壁画绘制技法制备不同颗粒度及浓度的彩绘颜料色样, 构建敦煌彩绘矿物颜料样本集, 建立敦煌壁画颜料颜色色标数据库。 以白卡纸为基底模拟敦煌地仗, 以动物骨胶为连接料, 选取北京天雅岩彩画研究所提供的敦煌矿物颜料, 依照敦煌壁画绘制技法制作模拟样本。 混色颜料样本以0.1的比例间隔设置浓度梯尺, 如表1所示, 以钛白和铅黑两种混色颜料制作浓度梯尺色样, 共制作模拟样本430个。

表1

Table 1

表1(Table 1)

表1 矿物颜料样本制备的浓度梯尺设置 Table 1 Concentration gradient setting for mineral pigment sample preparation 颜料号 浓度比例 Ⅰ 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 Ⅱ 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

表1 矿物颜料样本制备的浓度梯尺设置 Table 1 Concentration gradient setting for mineral pigment sample preparation

实验依照中国传统岩彩绘画技法重绘了“ 释迦摩尼佛像” , 并将图像颜料分布区域及成分进行了映射, 如图1所示。 实验选取颜料样本中土红、 雌黄、 铅丹、 密陀僧、 群青和石绿等6类颜料, 具体包括纯色土红颜料、 土红与钛白7∶ 3混色颜料、 纯色雌黄颜料、 纯色铅丹颜料、 纯色密陀僧颜料、 纯色群青颜料、 群青与钛白5∶ 5混色颜料、 颗粒度9#的纯色石绿颜料、 颗粒度11#的纯色石绿颜料、 颗粒度13#的石绿与钛白7∶ 3混色颜料、 土红与雌黄5∶ 5混色颜料, 通过颜料颗粒度、 矿物颜料与钛白混合及矿物颜料两两混合呈现不同色调。

图1

Fig.1

Figure Option ViewDownloadNew Window

图1 彩绘模拟图像中颜料的映射区域及对应色块 (a): 土红; (b): 土红∶ 钛白=7∶ 3; (c): 雌黄; (d): 铅丹; (e): 密陀僧; (f): 群青; (g): 群青∶ 钛白=5∶ 5; (h): 石绿(9#); (i): 石绿(11#); (j): 石绿(13#)∶ 钛白=7∶ 3; (k): 土红∶ 雌黄= 5∶ 5; (l): 模拟图像Fig.1 Mapping areas and their color blocks of pigments in an analog image (a): Earth red; (b): Earth red∶ titanium white=7∶ 3; (c): Orpiment; (d): Lead tetroxide; (e): Lithargyrum; (f): Ultramarine blue; (g): Ultramarine blue∶ titanium white=5∶ 5; (h): Mineral green(9#); (i): Mineral green(11#); (j): Mineral green(13#)∶ titanium white=7∶ 3; (k): Earth red∶ Orpiment= 5∶ 5; (l): The analog image

本文采用X-Rite公司Ci64UV积分球式分光光度计测量430个色块可见光波段范围(400~700 nm)的光谱反射率。 设备采用d/8° 几何测量条件, 6 mm开孔直径, SCE测量模式, UV测量模式, 通过测量值三次求平均的方法消除测量随机误差, 将光谱反射率与色度值、 浓度值、 颜料粒径、 颜料成分等属性关联, 建立敦煌壁画颜料颜色色标数据库。

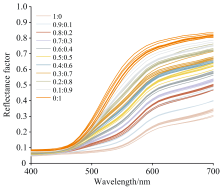
以土红雌黄混色颜料为例。 首先, 将土红设为Ⅰ 号颜料, 雌黄设为Ⅱ 号颜料, 按照表1浓度比例混合, 制备出第1组11个浓度梯尺的混色样本; 其次, 重复以上步骤进行样本制作, 共制作出8组11个浓度梯尺的混色样本; 最后, 使用分光光度计对88个土红雌黄混色样本进行光谱测量。 土红雌黄混色颜料样本在不同浓度梯尺的光谱反射率如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 矿物颜料两两混合后在11个浓度梯尺下的8组光谱反射率Fig.2 Eight sets of spectral reflectance of mineral pigments mixed in pairs at 11 concentration gradients

1.2.1 训练样本数据

数据集的增强与扩充能够增加训练数据的多样性, 缓解过拟合现象, 提高模型泛化能力, 进而提高模型性能。 一般来说, 训练样本越多, 可以使模型对输入数据的微小扰动具有更好的鲁棒性, 提高模型的稳定性, 预测结果更加精确。 基于此, 本文通过非线性插值将0.1浓度梯尺混色样本数据库, 扩充为0.05比例间隔的混色样本数据库, 即将原来的11个比例间隔为0.1的颜料浓度梯尺样本数据扩充为21个比例间隔为0.05的颜料浓度梯尺样本数据。 并由8组样本的光谱反射率数据中随机选取5组进行训练样本。 训练样本不同浓度梯尺的混色样本光谱反射率如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 采集到的21个浓度梯尺下训练样本的光谱反射率Fig.3 Spectral reflectance of the training samples collected at 21 concentration gradients

1.2.2 测试样本数据

测试样本用于检验模型性能, 与训练样本类似, 测试样本数量过少同样会增加模型误差。 本文通过计算RMSE等评价指标来衡量真实值与预测值的一致程度。 同一个浓度梯度下的样本制备时难免会产生误差, 从而导致同一个浓度梯度下样本的光谱反射率不同, 当测试样本只有一组时, 通过光谱反射率计算出的预测值同样只有一组, 所得评价指标不足以证明模型精度, 因此本文通过三组测试样本对所建模型进行检验, 以此来减小误差。 实验选取8组样本数据中剩余的3组, 参照训练样本, 对其进行非线性插值扩充, 每组样本数据均具有21个浓度梯尺, 以保证训练集与测试集的一致性。 测试样本不同浓度梯尺的混色样本光谱反射率如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 采集到的21个浓度梯尺下测试样本的光谱反射率Fig.4 Spectral reflectance of the test samples collected at 21 concentration gradients

K-M模型^[11]通过光谱反射率计算吸收系数和散射系数之比, 对于不透明颜料, 可由式(1)表示

KS=(1-R)22R(1)

式(1)中, R为颜料的光谱反射率; K和S为颜料的吸收和散射系数。 混合颜料与各基色颜料之间的吸收散射比关系, 如式(2)所示

KSmixture=c1KS1+c2KS2+…+cnKSn(2)

式(2)中, (K/S)_mixture为混合颜料的吸收和散射系数之比; (K/S)_i为第i个基色颜料的吸收和散射系数之比; n为混合颜料总数; c_i为第i个基色颜料的浓度。

贝叶斯优化算法(Bayesian optimization algorithm, BOA)属于迭代算法, 广泛应用于超参数优化问题^[12]。 BOA通过构建代理模型来建立目标函数与超参数的关系, 并使用贝叶斯推断不断根据先验知识和已有数据进行模型优化^[13], 从而最大程度上减少真实目标函数的评估次数, 贝叶斯推断如式(3)所示

p(y│D)=p(D|y)p(y)p(D)(3)

式(3)中, p(y│D)为后验概率分布, 表示对超参数的估计; p(D|y)为似然函数, 表示给定观测数据下, 超参数的似然性; p(y)为先验概率分布, 表示在没有观测数据的情况下对超参数的初始估计; p(D)为边缘似然概率, 表示得出固定超参数的概率。

由于高斯过程模型的灵活性和可追踪性^[14], 本文采用高斯过程作为目标函数建模的代理模型, 通过已经进行的评估结果来估计超参数的概率分布。 高斯过程是一组随机变量的无限集合, 其中任意有限个变量的联合分布服从多元高斯分布, 如式(4)所示

f(x)~GP(m(x), k(x, x'))(4)

式(4)中, GP为高斯过程, 表示连续域上的无限多个服从高斯分布的随机超参数所组成的随机过程; f(x)为高斯过程中的随机函数; x为输入超参数; m(x)为均值函数, 表示超参数的整体趋势; k(x, x')为协方差函数, 表示不同输入超参数之间的相关性。

在优化超参数时, BOA能够在较少的评估次数内寻找到具有较高性能的超参数组合; 能够更加智能地选择下一个超参数组合进行评估, 以使目标函数的值更大可能地提升; 能够充分利用已有数据, 通过不断更新代理模型来进行全局优化, 从而更有效地找到最优解。

BOA的工作流程如图5所示。 具体步骤如下: (1)输入待优化的超参数空间; (2)选择初始的样本点集合; (3)使用已有的样本点集合, 建立高斯过程模型来评估超参数的概率分布; (4)使用熵搜索策略选择下一个样本点x_i+1, 该方法旨在最大化对超参数不确定性的贡献, 以尽可能的减少搜索超参数时的不确定性; (5)根据选择的样本点, 在真实的目标超参数上进行函数评估, 并获取新的观测值y_i+1; (6)将新的观测值纳入高斯过程模型, 使用贝叶斯推断来更新超参数的概率分布, 并获得新的观测集(x_i+1, y_i+1)∈ D; (7)迭代了n次之后, 输出历史最优配置组合及其评估指标值, 得出最佳超参数。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 贝叶斯优化算法流程图Fig.5 Workflow of the Bayesian optimization algorithm

前馈回归神经网络(feedforward regression neural network, FRNN)的第一个全连接层与输入值相连, 随后的每一层与前一层相连, 即上下层之间实现全连接, 而同一层的神经元之间无连接, 如图6所示。 输入神经元与隐含层神经元之间是网络的权值, 其意义是两个神经元之间的连接强度。 隐含层或输出层任一神经元将前一层神经元传来的信息进行整合, 通常还会在整合过的信息中添加一个阈值, 模仿生物学中神经元必须达到一定的阈值才会触发的原理, 然后将整合过的信息作为该层神经元的输出。 FRNN在解决回归问题时具有较强的自学习和自适应能力, 但预测结果表明其对超参数选取的要求高, 若选取不当会导致性能降低。 故需要根据图5所示流程, 设置最大迭代次数为1 000, 利用BOA对FRNN的网络结构、 激活函数和正则化强度等超参数进行优化, 从而构建BOA-FRNN模型。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 FRNN模型的结构Fig.6 The structure of FRNN model

2.3.1 网络结构优化

本文使用数据库中31维的光谱反射率预测1维的浓度映射分布图谱, 因此设置网络模型的输入层大小为31, 输出层大小为1。 对于隐含层, 按照图5所示步骤, 基于BOA寻找其大小从而使得网络结构最佳, 设置搜索范围为1~300, 最终优化出的隐含层大小为1, 从而构建出具有输入层、 隐含层和输出层的三层神经元网络。

2.3.2 激活函数优化

激活函数是神经网络的重要组成部分, 分为线性和非线性, 连续且可微。 神经网络的隐含层需要使用非线性激活函数, 目的是将非线性特性引入到神经网络中, 强化网络的学习能力。 若使用线性激活函数, 则具有隐含层的神经网络将成为一个巨大的线性回归模型, 这对于从光谱数据中学习复杂模式毫无用处。 输入层只保存输入数据, 不执行任何计算, 因此选取与隐含层相同的激活函数。 本文通过构建混合矿物颜料的浓度预测模型来解决回归问题, 输出层需要使用线性激活函数。

神经网络中使用的激活函数类型不同, 神经网络模型的性能便会存在较大差异, 因此需要选取适合于本文网络模型的激活函数以达到模型性能最大化。 本文基于BOA搜索最佳的激活函数, 设置搜索范围为ReLU、 LeakyReLU、 logsig、 dlogsig、 tansig和dtansig这6种回归问题中常用的非线性激活函数对输入层和隐含层的激活函数进行超参数优化, 搜索出的激活函数为tansig。 对于输出层, 本文使用线性激活函数purelin。 函数tansig的解析式为tanh(x)= ex-e-xex+e-x; 函数purelin的解析式为purelin(x)=x。

2.3.3 BOA-FRNN模型

本研究设置最大迭代次数为1 000, 根据图5所示流程, 基于BOA优化FRNN得出的网络输入层大小为31, 激活函数为tansig; 隐含层大小为1, 激活函数为tansig; 输出层大小为1, 激活函数为purelin; 正则化强度约为1.619× 10^-5。 综上构建出BOA-FRNN模型如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 BOA-FRNN模型Fig.7 BOA-FRNN model

本文定义BOA-FRNN模型将每个全连接层的输入乘以一个权重矩阵, 然后加上一个偏置向量。 权重矩阵决定了每个输入数据的特征对预测值的影响, 偏置向量避免了所有特征取值为0时得不出预测值的情况。 BOA-FRNN模型的权重调整如式(5)和式(6)所示, 偏置调整如式(7)式和(8)所示。

wij(t+1)=-η∂E∂wij+wij(t)(5)

wjk(t+1)=-η∂E∂wjk+wjk(t)(6)

bij(t+1)=-η∂E∂bij+bij(t)(7)

bjk(t+1)=-η∂E∂bjk+bjk(t)(8)

式(5)— 式(8)中, E为网络输出与实际输出样本之间的误差平方和; η 为网络的学习速率, 即权重调整幅度; w_ij(t)为t时刻输入层第i个神经元与隐含层第j个神经元的连接权重; w_ij(t+1)为t+1时刻输入层第i个神经元与隐含层第j个神经元的连接权重; w_jk(t)为t时刻隐含层第j个神经元与输出层第k个神经元的连接权重; w_jk(t+1)为t+1时刻输入层第j个神经元与隐含层第k个神经元的连接权重。 b为神经元的偏置, 下标意义与权重相同。

实验采用均值(Mean)、 方差(Variance)、 标准差(standard deviation, SD)、 均方根误差(RMSE)和决定系数(R²)五个评价标准评估模型性能。 令t_i为颜料浓度的真实值; p_i为模型计算的预测值; x_i=|t_i-p_i|。 五个评价标准的具体计算公式如式(9)— 式(13)所示

Mean=∑1nxin(9)

Variance=∑1n(xi-Mean)2n-1(10)

SD=∑1n(xi-Mean)2n-1(11)

RMSE=∑1nxi2n(12)

R2=1-∑1nxi2∑1n(ti-t-i)2(13)

式(9)— 式(13)中, x_i为浓度差; t-i为真实值的平均值; n为样本数量。 若均值、 方差和标准差越小, RMSE越接近于0, R²越接近于1, 则说明预测模型性能越高, 获取的颜料浓度映射更准确。

实验对比分析了六种光谱预测模型的性能, 包括双常数K-M模型^[11]、 BP网络模型^[15]、 SVM分类器模型^[16]、 FRNN网络模型^[17]、 BOA-SVM模型^[18]和本文构建的BOA-FRNN模型, 分析结果如表2所示。 通过分析数据可知, BOA-FRNN光谱模型对于训练集的均值、 方差和标准差最小, RMSE为0.330%, R²为99.99%, 较其他模型最优; 测试集的均值、 方差和标准差最小, RMSE为1.827%, R²为99.66%, 较其他模型最优。 图8为六种光谱模型对颜料浓度的预测准确率, 相较于其他模型, BOA-FRNN光谱模型对于训练集和测试集的预测结果更加收敛。 综上分析, 本文所构建的BOA-FRNN光谱模型更加适用于预测矿物颜料的浓度映射分布图谱。

表2

Table 2

表2(Table 2)

表2 六种光谱模型的预测分析结果 Table 2 Predictive analysis results of six spectral models 光谱模型 Mean Variance SD RMSE R2 K-M 训练集/% 3.938 0.075 2.734 4.795 96.59 测试集/% 2.708 0.050 2.246 3.507 98.48 BP 训练集/% 2.292 0.033 1.807 2.913 99.02 测试集/% 4.720 0.192 4.381 6.416 96.23 SVM 训练集/% 1.169 0.012 1.092 1.591 99.72 测试集/% 2.757 0.123 3.505 4.438 98.15 FRNN 训练集/% 1.854 0.039 1.984 2.708 99.12 测试集/% 3.102 0.051 2.259 3.827 98.36 BOA-SVM 训练集/% 0.622 0.002 0.491 0.790 99.93 测试集/% 2.480 0.086 2.939 3.828 98.54 BOA-FRNN 训练集/% 0.260 0.001 0.205 0.330 99.99 测试集/% 1.289 0.017 1.305 1.827 99.66

表2 六种光谱模型的预测分析结果 Table 2 Predictive analysis results of six spectral models

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 六种光谱模型对颜料浓度的预测准确率 (a): 双常数K-M模型; (b): BP模型; (c): SVM模型; (d): FRNN模型; (e): BOA-SVM模型; (f): BOA-FRNN模型Fig.8 Prediction accuracy of pigment concentration by six spectral models (a): Two-Constant K-M model; (b): BP model; (c): SVM model; (d): FRNN model; (e): BOA-SVM model; (f): BOA-FRNN model

本文比较分析了双常数K-M模型、 BP模型、 SVM模型、 FRNN模型、 BOA-SVM模型和构建的BOA-FRNN模型获取矿物颜料浓度映射的精度。 由于纯色颜料只起到设置浓度梯尺的作用, 因此只保留混色颜料色样, 即只保留0.9∶ 0.1~0.1∶ 0.9的比例间隔为0.1的浓度梯尺数据。 以混合颜料中的土红浓度为例, 六种光谱模型预测出的浓度精度如表3所示, 预测结果与真实结果的对比图如图9所示, 六种光谱预测模型的精度排序为: BOA-FRNN> BOA-SVM> FRNN> SVM> K-M> BP。 其中BOA-FRNN模型的预测结果与真实结果之间的重合度更高, 更符合真实值。

表3

Table 3

表3(Table 3)

表3 六种光谱模型预测出的浓度映射分布 Table 3 Concentration mapping distribution predicted by the six spectral models 颜料号 土红浓度 真实值 预测值 K-M BP SVM FRNN BOA-SVM BOA-FRNN 1 0.9 0.878 2 0.919 9 0.916 5 0.863 8 0.897 2 0.922 4 2 0.9 0.886 8 0.858 6 0.914 9 0.861 9 0.901 8 0.921 0 3 0.9 0.807 1 0.705 9 0.867 1 0.848 5 0.888 7 0.899 0 4 0.8 0.771 8 0.614 0 0.805 8 0.772 0 0.808 1 0.805 8 5 0.8 0.792 3 0.547 9 0.803 4 0.771 0 0.808 2 0.811 7 6 0.8 0.742 4 0.490 7 0.788 6 0.776 2 0.800 3 0.804 3 7 0.7 0.664 7 0.417 0 0.695 1 0.687 9 0.703 9 0.694 6 8 0.7 0.687 4 0.211 9 0.669 7 0.637 9 0.662 7 0.685 8 9 0.7 0.671 2 0.000 4 0.701 0 0.697 3 0.709 2 0.703 8 10 0.6 0.582 4 0.922 2 0.597 4 0.599 7 0.604 6 0.596 4 11 0.6 0.611 6 0.881 7 0.585 7 0.559 7 0.579 2 0.602 7 12 0.6 0.584 5 0.755 9 0.592 4 0.593 3 0.598 9 0.598 3 13 0.5 0.501 2 0.621 0 0.499 8 0.512 1 0.501 3 0.508 7 14 0.5 0.527 0 0.498 7 0.496 7 0.474 9 0.485 4 0.511 5 15 0.5 0.485 6 0.388 6 0.496 7 0.510 5 0.499 0 0.502 9 16 0.4 0.440 0 0.275 8 0.432 3 0.424 0 0.424 0 0.409 2 17 0.4 0.402 2 0.107 0 0.364 5 0.374 3 0.360 0 0.381 2 18 0.4 0.402 2 0.064 4 0.396 0 0.402 4 0.393 6 0.399 8 19 0.3 0.380 4 0.870 1 0.364 7 0.338 7 0.352 1 0.317 0 20 0.3 0.300 3 0.802 4 0.257 0 0.276 8 0.250 9 0.279 6 21 0.3 0.318 8 0.706 5 0.309 0 0.313 5 0.309 2 0.301 1 22 0.2 0.246 7 0.597 8 0.209 9 0.175 3 0.188 1 0.161 3 23 0.2 0.178 6 0.531 1 0.140 0 0.168 5 0.137 5 0.170 2 24 0.2 0.237 6 0.439 6 0.197 6 0.206 0 0.190 3 0.202 3 25 0.1 0.125 0 0.336 2 0.055 1 0.041 9 0.026 5 0.051 0 26 0.1 0.062 6 0.205 8 0.000 7 0.048 2 0.027 6 0.065 0 27 0.1 0.179 4 0.099 9 0.129 5 0.107 4 0.105 9 0.102 6

表3 六种光谱模型预测出的浓度映射分布 Table 3 Concentration mapping distribution predicted by the six spectral models

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 预测结果与真实结果之间的对比图 (a): 双常数K-M模型; (b): BP模型; (c): SVM模型; (d): FRNN模型(e): BOA-SVM模型; (f): BOA-FRNN模型Fig.9 Comparison between predicted and ground truth (a): Two-Constant K-M model; (b): BP model; (c): SVM model; (d): FRNN model; (e): BOA-SVM model; (f): BOA-FRNN model

六种模型真实值与预测值浓度差统计曲线如图10所示, 数据表明, 本文提出的BOA-FRNN模型预测的27个浓度差整体小于物理模型(双常数K-M模型)和网络模型(BP、 SVM、 FRNN和BOA-SVM), 且误差数据波动小, 结果更加稳定。 综上分析, 本文提出的BOA-FRNN模型在根据光谱反射率预测矿物颜料的浓度映射分布时性能更加稳定, 不容易陷入局部最优, 有效的提高了矿物颜料浓度的预测准确率。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 六种光谱模型的浓度差曲线Fig.10 Concentration difference curves for the six spectral models