Moisture content is a crucial indicator for assessing the quality of agricultural products. However, the strong absorption of THz waves by environmental moisture, along with the overlapping absorption characteristics of other components in agricultural products within the THz spectral range, poses significant challenges for accurately predicting moisture content using THz spectroscopy. To thoroughly investigate the effectiveness of adaptive signal decomposition-based denoising methods, this study specifically selects the construction of a THz-ATR prediction model for peanut moisture content as a case study. The experiment uses Yuanhua 308 peanuts as samples. To prepare samples with different moisture content levels, the peanut samples were placed in an environment at 40 ℃ and 100% relative humidity. Each day, a batch of samples was removed. After exposure to air for varying durations, samples were collected. A total of 12 batches and 48 samples were prepared.

The seed samples were crushed using the FW-200 high-speed universal grinder, and their moisture content was rapidly measured using the Mettler-Toledo HB43-S halogen moisture analyzer. The statistical information on moisture content for the 48 samples is shown in the Table 1 below.

Table 1

Table 1

Table 1 Statistical information of sample moisture content Sample size Min/% Max/% Average/% 48 4.22 30.27 12.93

Table 1 Statistical information of sample moisture content

The experiment utilized a TeraPulse 4000 terahertz time-domain spectroscopy (THz-TDS) system with an ATR accessory to collect the spectra of peanut samples, as shown in Fig.1. The spectrometer parameters were set as follows: the spectral range was 0.2~359.94 cm^-1, the resolution was 0.94 cm^-1, and each sample was scanned 500 times. The experimental environment temperature was maintained at 22 ℃. During the experiment, a SICOLAB mini air compressor was used to purge the sampling chamber with dry air, reducing the influence of environmental water vapor on THz spectral measurements.

Fig.1

	Figure Option ViewDownloadNew Window
	Fig.1 THz spectrometer and acquisition accessories (a): TeraPulse 4000 spectrometer; (b): ATR attachments

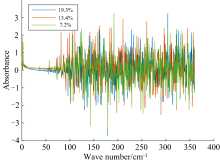
As representative examples, Fig.2 presents the absorbance spectra of peanut samples with moisture contents of 19.3%, 13.4%, and 7.2%, corresponding to high, medium, and low moisture levels relative to the overall sample average (12.93%). These samples were selected to illustrate typical spectral features under different moisture conditions. Spectral curve analysis indicates that in the range of 0.2~76 cm^-1, the spectral profiles are distinct yet highly similar and consistent, with no significant noise interference. However, in the range of 76~359.94 cm^-1, the signal exhibits drastic and irregular fluctuations, with no observable characteristic signals from the samples. This indicates that the THz spectra of peanut samples exhibit a significant non-uniform noise distribution.

Fig.2

	Figure Option ViewDownloadNew Window
	Fig.2 Absorbance spectra of peanut samples with different moisture contents

The adaptive signal decomposition method decomposes complex signals into multiple intrinsic mode functions or sub-signals, allowing the extraction of useful information while removing noise. This method does not require prior assumptions and can adaptively select an appropriate basis for decomposition, making it suitable for processing complex, non-stationary, and nonlinear signals.Since agricultural product THz spectral signals are affected by issues such as peak overlap due to complex matrices and dynamic, nonlinear interference from environmental and system noise, this study explores the applicability of typical adaptive signal decomposition methods— WT, EMD, and LMD— for THz spectral denoising. Additionally, given the significant non-uniformity in the noise distribution in peanut THz spectral signals, this study proposes improved methods: SLMD and PME-LMD.

1.4.1 Wavelet transform method

WT is a signal analysis method that combines time and frequency localization characteristics^[20]. Through scale transformation and translation operations, it enables multi-scale fine analysis of spectral data, achieving hightime-resolution analysis in high-frequency bands and high-frequency-resolution analysis in low-frequency bands, making it highly suitable for non-stationary signal processing. The continuous wavelet transform (CWT) of a one-dimensional signal f(t)f(t) can be expressed as the convolution of the signal with a series of wavelet mother functions, as shown in Equation (1)

CWT(a, b)=1|a|∫-∞+∞f(t)Ψt-badt(1)

Where CWT(a, b) represents the wavelet coefficients, a is the wavelet scale parameter, b is the wavelet translation parameter, Ψ (t) is the wavelet mother function, and Ψ ^* (t) denotes the complex conjugate of Ψ (t).

The essence of the wavelet transform is to project the THz absorbance spectrum of f(x) onto the wavelet function Ψ ^* (t), then apply threshold processing to the wavelet coefficients corresponding to different high and low frequencies, and finally reconstruct the signal^[21]. In the wavelet transform, selecting an appropriate wavelet basis and the number of decomposition levels significantly impac denoising performance.

1.4.2 Empirical mode decomposition method

EMD is a method for analyzing nonlinear and non-stationary time series. Compared with traditional methods, EMD generates basis functions directly from the signal data, making it intuitive and adaptive. Its core principle is to decompose the signal into several Intrinsic Mode Functions (IMFs) and reveal their time-frequency characteristics through the Hilbert transform, making it well-suited for processing nonlinear and non-stationary signals.

In the EMD algorithm, the definition of an IMF includes the following criteria: the number of extrema and zero-crossings in the data must be equal or differ by at most one, and the mean of the envelope defined by the local extrema must be zero at any given point. An IMF intuitively represents the amplitude and frequency variations of the data over time.

The steps of the EMD algorithm are as follows:

① Identify the local maxima and minima of the signal and connect these points using cubic spline interpolation to form the upper envelope u(t) and lower envelope v(t).

② Calculate the mean of the upper and lower envelopes m(t), using the following formula

m(t)=u(t)+v(t)2(2)

③ The formula for calculating the component functions in the EMD algorithm is as follows

h(t)=x(t)-m(t)(3)

④ Check if h(t) satisfies the IMF conditions. If it does, label it as the first IMF component c₁(t); if it does not, treat h(t) as the new signal and repeat the previous steps until the IMF is obtained. Once an IMF component is extracted from the original signal, remove it from the signal, then repeat the above process on the remaining signal to obtain the next IMF component. This process is repeated until EMD algorithm's termination conditions are met, indicating that the signal has been fully decomposed. The termination condition of the EMD algorithm is based on the Cauchy convergence criterion, which is specifically defined by the following formula

$S D_{k}=\frac{\displaystyle\sum_{t=0}^{T}\left|h_{k-1}(t)-h_{k}(t)\right|^{2}}{\displaystyle\sum_{t=0}^{T} h_{k-1}(t)^{2}}$(4)

Where: T represents the signal length. The decomposition ends when SD_k is smaller than the set threshold.

1.4.3 Local mean decomposition method

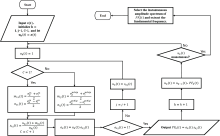
LMD is a method for time-frequency analysis of multi-component signals, proposed by Jonathan S. Smith et al.^[22] in 2005. LMD adaptively decomposes a complex signal into a collection of single-component amplitude and frequency-modulated signals, accurately reflecting the time-frequency characteristics of the original signal. LMD can automatically adjust the decomposition process based on the signal's features, effectively extracting instantaneous frequency and amplitude information. Compared to EMD, LMD performs better in solving issues such as modal aliasing, endpoint effects, and curve fitting. By extracting finer local features, LMD reduces false components and over- or under-enveloping problems. Due to its high adaptability and precise time-frequency analysis capability, LMD is widely regarded in the field of non-stationary signal processing ^[23].

The specific decomposition steps of LMD are shown in Fig.3.

Fig.3

	Figure Option ViewDownloadNew Window
	Fig.3 Flowchart of the LMD decomposition steps

1.4.4 Segmented local mean decomposition method

Based on the spectral analysis in section 1.3, it is evident that agricultural product THz spectra exhibit significant non-uniform noise distribution characteristics. Therefore, this study proposes the SLMD method, which first divides the THz spectrum into several segments and then applies Local Mean Decomposition and signal reconstruction to each segment^[24].

The SLMD method improves the flexibility and accuracy of complex signal processing by handling different noise characteristics in various segments. It is suitable for processing non-stationary and nonlinear signals. This segmented processing approach effectively integrates the local characteristics of the signal with its overall structure, enabling a more refined adaptation to the non-uniform noise distribution within the signal. It holds promise for further improving the effectiveness and accuracy of signal processing.

1.4.5 Piecewise mirror extension local mean decomposition method

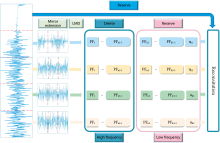
When using the SLMD method, the spectrum needs to be segmented, and each segment requires independent LMD denoising. Too many segmentation points can lead to divergence at both ends of the spectrum and cause the signal to spread toward the center, exacerbating endpoint effects^[25]. To address this issue, this paper introduces the Mirror Extension technique^{[26, 27]}, based on SLMD, and proposes the PME-LMD method. Mirror extension effectively prevents endpoint effects at the beginning and end of signal processing, maintaining the signal's continuity and integrity during denoising, thereby improving the endpoint effects of SLMD^[28]. The denoising process of the PME-LMD method is shown in Fig.4.

Fig.4

	Figure Option ViewDownloadNew Window
	Fig.4 PME-LMD denoising process

The PME-LMD method follows the steps below:

(1) Divide the spectral signal into several intervals based on the distribution levels of noise in the spectrum. This step aims to process regions with different noise levels more precisely.

(2) Perform mirror extension on each divided interval, i.e., extend the mirror image to the left and right, forming the piecewise mirror extension (PME) spectrum.

(3) Use LMD to decompose each PME spectrum, obtaining a series of intrinsic mode functions (PF_s) and a final residual component u_k. The goal is to extract components with different frequencies from the signal and identify noise components.

(4) Analyze the decomposition results of each PME spectrum, remove the high-frequency noise components from the spectra PF_s, and retain the low-frequency components that reflect the essential characteristics of the signal. Then, reconstruct the signal after the removal to obtain the denoised THz spectrum.

SVR constructs the optimal regression hyperplane by minimizing structural risk, emphasizing the model's generalization ability. SVR is suitable for small sample sizes, high-dimensional, and nonlinear problems, providing strong nonlinear approximation and generalization through high-dimensional mapping, a unique loss function, and regularization. In this study, SVR is used to construct a quantitative THz analysis model for peanut moisture content.

In this study, the performance of the regression model is evaluated using three metrics: Root Mean Square Error (RMSE), Coefficient of Determination (R²), and Mean Absolute Percentage Error (MAPE).

(1) Root Mean Square Error (RMSE): It is the square root of the average of the squared differences between the observed values and the model's predicted values. It is a commonly used metric to assess the magnitude of the model's prediction error. The calculation formula is as follows:

$\mathrm{RMSE}=\sqrt{\frac{1}{n} \displaystyle\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}$(5)

Where y_i is the actual value, $\hat{y}_{i}$ is the predicted value, and RMSE is the number of samples. The smaller the value, the smaller the difference between the model's predicted values and the actual values, indicating better model performance.

(2) Coefficient of Determination (R²): This is an indicator of the model's ability to explain the variability of the variables, i.e., the proportion of the data variability that can be explained. The calculation formula is as follows:

$R^{2}=1-\frac{\displaystyle\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\displaystyle\sum_{i=1}^{n}\left(y_{i}-\bar{y}_{i}\right)^{2}}$(6)

Where $\bar{y}_{i}$ is the mean of the actual values, the value of R² typically ranges from 0 to 1. The closer the value is to 1, the better the model explains the data's variability. The higher the R² value, the better the model's fit.

(3) Mean Absolute Percentage Error (MAPE): This is the average of the absolute differences between the observed values and the predicted values, expressed as a percentage of the actual values. It is an indicator of prediction accuracy and is suitable for assessing the prediction performance of data on different scales. The calculation formula is as follows:

$\text { MAPE }=\frac{100 \%}{n} \displaystyle\sum_{i=1}^{n}\left|\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right|$(7)

The smaller the MAPE value, the higher the model's prediction accuracy. It is suitable for comparing model performance across datasets of different magnitudes.

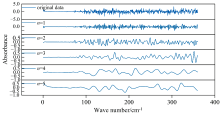
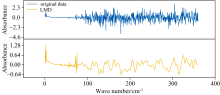
In wavelet transform denoising, the selection of the wavelet basis function and the decomposition level significantly affect the denoising effect. The Sym8 wavelet function, with its compact support, good continuity, and symmetry, is suitable for denoising signals with good continuity. Therefore, the Sym8 wavelet was chosen as the wavelet basis function. To compare denoising effects across different decomposition levels, the absorbance spectrum of a sample with 13.4% RH was used as an example. The original sample was decomposed into 5 levels, as shown in Fig.5, where n represents the decomposition level. From the Figure, it can be observed that as the decomposition level increases, spectral details are lost, and the signal distortion gradually intensifies.

Fig.5

	Figure Option ViewDownloadNew Window
	Fig.5 Reconstructed spectra at different decomposition scales using the Sym8 wavelet basis function

The peanut samples were randomly divided into training and test sets at a 3∶ 1 ratio, with 36 for training and 12 for testing. The SVR model was used to develop a quantitative analysis model for peanut moisture content at different decomposition levels, and the test set results are shown in the Table 2.

Table 2

Table 2

Table 2 Quantitative model indicators for peanut moisture content based on WT denoising processing Decomposition Scale RMSE R2 MAPE 0 0.076 0.372 0.547 1 0.020 0.791 0.197 2 0.051 0.347 0.462 3 0.054 0.314 0.361 4 0.068 0.416 0.501 5 0.093 0.128 0.822

Table 2 Quantitative model indicators for peanut moisture content based on WT denoising processing

As shown in the Table 2, as the wavelet decomposition level increases, the evaluation metrics deteriorate, and the denoising effect declines. This indicates that a decomposition level of 1 is optimal for the THz absorbance spectrum using the Sym8 wavelet function. As illustrated in the Figure 5, the wavelet denoising result at a decomposition scale of 1 effectively removes most high-frequency noise while preserving the primary trend of the original absorbance spectrum without denoising.

The denoising performance of WT is highly influenced by the choice of wavelet basis function and decomposition level, and its ability to handle nonlinear signals is limited. In contrast, EMD is a fully adaptive signal decomposition method that does not require a predefined basis function, making it suitable for processing nonlinear and non-stationary signals. Using the absorbance spectrum of a sample with a moisture content of 13.4% RH as an example, the EMD denoising result is shown in Fig.6. The processed absorbance spectrum appears smoother with reduced fluctuations, but some noise and mode mixing remain.

Fig.6

	Figure Option ViewDownloadNew Window
	Fig.6 Sample spectrum before and after EMD denoising processing

Using the same training and testing sets as in Section 2.1, an SVR model for peanut moisture content was constructed, with the results shown in the Table 3. The evaluation metrics of the model based on the EMD-processed absorbance spectrum were superior to those of the unprocessed original spectrum, indicating that this denoising method can enhance the signal-to-noise ratio (SNR) of the spectrum to some extent. However, its performance was inferior to that of WT, suggesting that EMD may suffer from severe mode mixing and endpoint effects, resulting in suboptimal processing ^[29].

Table 3

Table 3

Table 3 Quantitative model metrics for peanut moisture content based on EMD denoising processing Denoising method Number of windows RMSE R2 MAPE None 1 0.076 0.372 0.547 EMD 1 0.064 0.423 0.412

Table 3 Quantitative model metrics for peanut moisture content based on EMD denoising processing

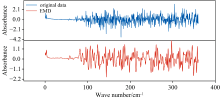
Due to the significant uneven distribution of noise in the peanut THz spectra, the noise is less noticeable in the < 76 cm^-1 region, while it significantly increases in the > 76 cm^-1 region. Therefore, the experiment first retains the spectral range with wavenumbers < 76 cm^-1, and applies LMD denoising to the region with significant noise (> 76 cm^-1). The high-frequency component is removed, while the remaining components are retained and the spectrum is reconstructed. Fig.7 shows the spectra before and after LMD processing. The LMD-processed spectrum is smoother and exhibits less signal fluctuation compared to the original spectrum. Therefore, LMD can effectively remove substantial noise, but it may also lead to over-smoothing, resulting in the loss of important features and details in the signal.

Fig.7

	Figure Option ViewDownloadNew Window
	Fig.7 Sample spectra before and after LMD denoising treatment

Using the training and testing sets from Section 2.1, the results of the peanut moisture content SVR model are shown in the Table 4. The model performance after LMD treatment is better than that of the model without denoising preprocessing and the model after EMD treatment, indicating that LMD is effective in reducing spectral noise and improving spectral quality. However, considering that there may still be uneven noise distribution in the wavenumber range > 76 cm^-1, applying uniform LMD treatment to this range could lead to signal distortion in the noise-free or low-frequency noise regions. Therefore, the modeling effect still needs further improvement.

Table 4

Table 4

Table 4 Peanut moisture content quantitative model indicators based on LMD denoising processing Denoising method Number of windows RMSE R2 MAPE None 1 0.076 0.372 0.547 LMD 1 0.042 0.560 0.152

Table 4 Peanut moisture content quantitative model indicators based on LMD denoising processing

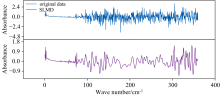
To address uneven spectral noise, this paper proposes the SLMD method. By dividing the spectrum into segments, applying LMD decomposition, and then reconstructing, SLMD achieves more precise denoising for uneven noise. In this study, the portion of the THz absorbance spectrum with higher noise, specifically the range from 76 to 359.94 cm^-1, is uniformly divided into 2, 3, 4, and 5 segments. Each segment undergoes LMD decomposition, removing high-frequency components PF₁, reconstructing the remaining components PF_s, and then stitching together the reconstructed spectra from different intervals to form the full spectrum. The SLMD-denoised absorbance spectrum for a sample with a moisture content of 13.4% RH, using a decomposition scale of 4, is shown in Fig.8. The denoised curve's smoothness falls between EMD and LMD, effectively reducing noise while better preserving the original signal's characteristics. This method optimizes complex noise distributions by decomposing and reconstructing across different noise intervals, achieving better denoising performance than single LMD.

Fig.8

	Figure Option ViewDownloadNew Window
	Fig.8 Sample spectra before and after SLMD denoising processing

Using the training and test sets from Section 2.1, the SVR results for the peanut moisture content model are shown in the Table 5. When applying the SLMD method with 3 and 4 spectral segmentations, the model performance is significantly better than that of a single LMD, especially when the segmentation number is 4, where the model performs optimally with an RMSE, R², and MAPE of 0.011, 0.872, and 0.042, respectively. However, when the number of segments is increased to 5, the model's performance decreases slightly compared to the 4-segment model. This phenomenon may be due to the SLMD method, with excessive segmentation, exacerbating its own endpoint effect. The endpoint effect may cause data divergence at the extremes. When there are too many segments, the spectral length of each window becomes shorter, meaning more data points are affected by the endpoint effect, which in turn affects the model's performance.

Table 5

Table 5

Table 5 Quantitative model indicators for peanut moisture content based on SLMD denoising treatment Modeling data Number of windows RMSE R2 MAPE 1 0.042 0.560 0.152 2 0.058 0.427 0.347 Absorbance 3 0.020 0.793 0.127 4 0.011 0.872 0.042 5 0.013 0.840 0.051

Table 5 Quantitative model indicators for peanut moisture content based on SLMD denoising treatment

To address the impact of endpoint effects on signal processing quality, this paper proposes the PME-LMD denoising method based on SLMD. This method effectively reduces data divergence at the endpoints by applying mirror extension at both ends of each segmented interval. Using the training and test sets from Section 2.1, the peanut moisture content SVR model was constructed, and the results are shown in the Table 6. After processing with the PME-LMD method, the constructed model demonstrates the best performance in terms of RMSE, R², and MAPE compared to other denoising methods such as CWT, LMD, and SLMD, with values of 0.010, 0.912, and 0.040, respectively. This result also confirms that PME-LMD effectively -mitigates the enhanced endpoint effects caused by excessive segmentation, thereby ensuring higher-quality signal reconstruction and analysis. It further illustrates the effectiveness of the PME-LMD method in reducing uneven noise and improving spectral quality, making it a practical and feasible approach for handling uneven noise in THz spectra of agricultural products.

Table 6

Table 6

Table 6 Quantitative model indicators of peanut moisture content based on adaptive signal decomposition denoising Modeling data Denoising Method Number of windows RMSE R2 MAPE Absorbance None 1 0.076 0.372 0.547 CWT 1 0.020 0.791 0.197 EMD 1 0.064 0.423 0.412 LMD 1 0.042 0.560 0.152 SLMD 4 0.011 0.872 0.042 PME-LMD 4 0.010 0.912 0.040

Table 6 Quantitative model indicators of peanut moisture content based on adaptive signal decomposition denoising