作者简介: 袁 博, 1982年生, 南阳理工学院信息工程学院讲师 e-mail: nylgyb@163.com
针对非支配排序遗传算法Ⅲ(NSGA-Ⅲ)在高光谱波段选择中存在的初始种群随机性强、 全局收敛性与局部多样性不平衡、 局部搜索效率低的问题, 提出一种地物分类驱动的多目标高光谱波段选择NSGA-Ⅲ改进算法(INSGA-Ⅲ)。 首先, 融合拉丁超立方采样(LHS)与参考点引导机制, 生成兼顾搜索空间覆盖性与目标空间聚焦性的高质量初始种群; 其次, 设计基于自适应旋转森林(ARF)的分类精度驱动项与基于皮尔逊相关系数的波段相关性惩罚项, 构建多目标适应度函数, 平衡全局探索与局部开发能力; 最后, 引入粒子群优化(PSO)的协同搜索机制, 提升局部搜索效率。 实验基于Indian Pines(农业场景)、 Pavia University(城市地物)、 Salinas(植被监测)及Botswana(矿物识别)四类高光谱数据集, 选取广泛应用的顺序前向选择(SFS)、 竞争性自适应重加权采样(CARS)、 多目标粒子群优化(MOPSO)、 基于分解的多目标进化算法(MOEA/D)及原始NSGA-Ⅲ算法作为基准算法, 验证INSGA-Ⅲ算法的普适优势。 实验结果表明, 在波段选择性能方面, INSGA-Ⅲ的信息熵与波段相关性指标相较于全部基准算法的均值, 信息熵指标提升8.5%, 波段相关性指标降低9.7%(冗余度减少)( p<0.01); 在SVM分类任务中, INSGA-Ⅲ的OA与Kappa系数分别领先全部基准算法的均值10.3%与11.6%( p<0.01); 算法效率方面, INSGA-Ⅲ达到90%帕累托前沿近似度的迭代次数较NSGA-Ⅲ减少32%, 且在添加25%高斯噪声的数据中(10次重复实验), 分类精度波动范围(标准差±1.23%)显著低于基准算法均值(±4.2%)。 该算法通过平衡信息量、 冗余度与分类精度目标, 可为农业作物监测、 城市地物分类及矿区矿物识别等任务提供高效、 鲁棒的波段选择方案, 显著降低高光谱数据处理的维度与成本。
ing at the issues of strong randomization in the initial population, imbalance between global convergence and local diversity, and low local search efficiency of the Non-dominated Sorting Genetic Algorithm Ⅲ (NSGA-Ⅲ) for hyperspectral band selection, an improved algorithm—INSGA-Ⅲ (Improved NSGA-Ⅲ driven by feature classification)—is proposed. Firstly, Latin Hypercube Sampling and a reference-point guidance mechanism were integrated to generate a high-quality initial population that ensures both comprehensive search space coverage and targeted focus in the objective space. Secondly, a classification accuracy-driven term based on the Adaptive Rotating Forest algorithm and a correlation penalty term based on the Pearson correlation coefficient were designed to construct a multi-objective fitness function that balances global exploration and local exploitation. Finally, the search mechanism of Particle Swarm Optimization was introduced to enhance regional search efficiency. Experiments are conducted on four types of hyperspectral datasets: Indian Pines (agricultural scenes), Pavia University (urban features), Salinas (vegetation monitoring), and Botswana (mineral identification). Widely used algorithms, including Sequential Forward Selection (SFS), Competitive Adaptive Reweighted Sampling (CARS), Multi-
ObjectiveParticle Swarm Optimization (MOPSO), Multi-
ObjectiveEvolutionary Algorithm Based on Decomposition (MOEA/D), and the original NSGA-Ⅲ, are selected as benchmarks to verify the universal advantages of INSGA-Ⅲ. Experimental results show that, in terms of band selection performance, INSGA-Ⅲ improves information entropy by 8.5% and reduces the band correlation metric by 9.7%, compared to the mean values of all benchmark algorithms ( p<0.01). In the SVM classification task, INSGA-Ⅲ outperforms the benchmark mean values by 10.3% in Overall Accuracy (OA) and 11.6% in Kappa coefficient ( p<0.01). Regarding algorithmic efficiency, INSGA-Ⅲ requires 32% fewer iterations to reach 90% Pareto front approximation than NSGA-Ⅲ, and shows significantly lower accuracy fluctuation (standard deviation ±1.23%) than the benchmark mean (±4.2%) under 25% Gaussian noise (averaged over 10 runs). The proposed algorithm provides an efficient and robust band selection scheme for applications such as agricultural crop monitoring, urban feature classification, and mineral identification, effectively balancing information content, redundancy, and classification accuracy, while significantly reducing the dimensionality and processing cost of hyperspectral data.
高光谱遥感技术凭借连续窄波段对地物光谱特征的精准捕获能力, 在地物分类领域展现出重要应用价值[1]。 然而, 海量数据中波段间存在的高度相关性与冗余信息, 导致数据存储和计算负担大幅增加, 同时也制约了分类精度的提升[2]。 波段选择是解决该问题的关键技术之一, 其核心任务是从大量光谱波段中提取最优子集, 使其同时达成高信息量、 低冗余度和高分类判别特征的多种目标[3]。
传统波段选择方法普遍存在信息表征能力与冗余控制效力的失衡问题。 例如, 顺序前向选择(sequential forward selection, SFS)因其贪心搜索策略, 容易引发波段冗余累积[4]; 竞争性自适应重加权采样(competitive adaptive reweighted sampling, CARS)受限于特定模型假设, 导致算法通用性不足[5]; 连续投影算法(successive projections algorithm, SPA)过度依赖数学投影而忽视光谱物理特性, 易丢失关键诊断波段[6]。
多目标优化算法可通过帕累托前沿(Pareto front)分析提供均衡解集, 但其中的多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法易陷入早熟收敛[7]; 基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)的性能易受权重向量与分解方法等因素影响[8]。
近年来, 多目标优化算法在高光谱波段选择中的应用主要围绕以下方向进行改进:
(1) 针对传统算法易陷入局部最优的问题, 研究者通过引入自适应机制提升性能。 例如, Wang等[9]提出混合灰狼优化器, 采用自适应权重更新平衡群体多样性与收敛速度, 在标准数据集上表现出显著优于基准算法的分类精度; Zhang等[10]设计的自适应粒子群优化(APSO-BS)通过动态调整学习因子, 在信息保留与冗余抑制的权衡中展现出明显优势。 然而, 此类方法仍严重依赖初始参数设置, 且对高维目标空间的探索效率有限。
(2) 为降低计算成本并提升解集多样性, 进行多任务与多模态优化, 例如, Wang等[11]提出多任务进化框架(MEMT-HBS), 通过任务间知识迁移在一次运行中生成多组最优子集, 但其迁移效率受波段光谱特性变化影响显著; Wei等[12]则利用子空间分解约束相邻波段选择, 有效降低了解集冗余度。
(3) 尝试将优化算法与深度学习结合。 例如, Kumar[13]通过3D CNN增强波段选择的上下文感知能力, 在典型数据集上达到当前领先的分类性能, 但模型训练需依赖大量标注数据。
(4) 利用非支配排序遗传算法Ⅲ (non-dominated sorting genetic algorithm Ⅲ , NSGA-Ⅲ )及其变体。 Gu等[14]通过改进距离支配关系, 在信息量与冗余度优化任务中有效提升了解集质量; Sawant[15]结合SVM分类器反馈优化目标权重, 显著增强了解集的实用性。 但NSGA-Ⅲ 在解集分布均匀性上仍存在不足, 且计算复杂度随目标数增加而显著上升[16]。
其中, NSGA-Ⅲ 因擅长处理高维多目标优化问题, 能够保证解具有良好的分布性, 逐渐成为波段选择的常用框架之一, 但仍存在三个重大缺陷: 初始种群随机性强、 全局收敛性与局部多样性不平衡、 局部搜索效率低, 严重制约了实际应用效果。 因此, 当前基于NSGA-Ⅲ 的波段选择研究亟需突破三大技术瓶颈: ①初始种群生成中先验信息(如光谱相关性)融合不足的瓶颈; ②多目标动态平衡(信息熵、 相关性、 分类精度)的适应度函数设计瓶颈; ③局部搜索受支配关系单一判据约束的精度优化瓶颈。
针对上述问题, 提出一种改进型NSGA-Ⅲ (INSGA-Ⅲ )波段选择算法, 通过信息保留、 冗余控制与分类精度提升的多目标协同优化, 系统性解决现有算法缺陷。 INSGA-Ⅲ 方法框架包含三项主要内容: 首先, 基于拉丁超立方采样[17](Latin hypercube sampling, LHS)结合参考点引导的初始化策略, 通过参考点约束LHS采样的空间分布, 确保种群覆盖Pareto前沿热点区域, 突破NSGA-Ⅲ 随机初始化的性能瓶颈; 其次, 引入基于自适应旋转森林[18](adaptive rotation forest, ARF)的分类精度驱动项, 以及基于皮尔逊相关系数的波段相关性惩罚项, 创建分类精度导向的动态适应度函数, 平衡全局收敛性与局部多样性, 增强多目标权衡的可控性; 第三, 建立粒子群优化[19](particle swarm optimization, PSO)与遗传算法的协同优化机制, 在遗传操作后执行局部搜索, 结合动态惯性权重加速收敛过程, 实现全局探索与局部优化的动态平衡。
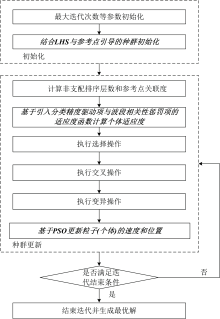
INSGA-Ⅲ 算法流程如图1所示, 其中粗斜体代表相对于NSGA-Ⅲ 的核心改进项。 INSGA-Ⅲ 算法具体步骤如下:
(1)完成算法初始化。 首先, 对算法的交叉概率、 变异概率、 最大迭代次数、 帕累托前沿稳定性指标等参数进行初始化; 其次, 以LHS结合参考点引导, 取代NSGA-Ⅲ 算法的随机初始化, 实现高质量的种群初始化。
(2)进入种群更新的迭代过程。 首先, 统计个体的非支配排序层数和参考点关联度, 并基于引入分类精度驱动项与波段相关性惩罚项的适应度函数计算个体适应度; 其次, 依据个体适应度计算结果, 依次执行个体的选择操作、 交叉操作和变异操作; 然后, 基于PSO算法更新粒子(个体)的速度和位置, 完成一次种群更新。
(3)检验当前是否满足迭代结束条件, 即达到最大迭代次数或满足帕累托前沿稳定性指标。 如果满足上述任何一项条件, 则结束迭代过程并生成最优解; 否则开始下一轮种群更新的迭代, 直至满足任意一项迭代条件。
INSGA-Ⅲ 与NSGA-Ⅲ 关于种群初始化算法、 适应度函数和局部搜索策略这三个核心模块的对比如表1所示。
| 表1 INSGA-Ⅲ 与NSGA-Ⅲ 的核心模块对比 Table 1 Comparison of core modules between INSGA-Ⅲ and NSGA-Ⅲ |
NSGA-Ⅲ 采用随机种群初始化算法, 在高维波段选择中易生成分布稀疏且偏离鉴别性光谱特征的初始解, 导致无法有效捕捉地物间的细微差异, 容易加剧类别不平衡下的解集偏差, 延长收敛周期并降低帕累托前沿的物理可解释性。
针对该问题, INSGA-Ⅲ 采用了LHS与参考点引导相结合的初始化算法, 首先采用LHS在波段组合空间中生成均匀候选解, 然后结合参考点筛选出目标空间分布最优的个体作为初始种群。 其中, LHS能够通过分层正交策略在解空间内均匀采样, 缓解随机初始化带来的高维决策空间采样偏差, 确保初始解覆盖鉴别性波段组合, 提升全局探索效率; 参考点引导则通过基于均匀分布的参考点划分目标空间, 直接优化目标空间分布, 并通过关联个体与参考点维持解集的分布性与收敛性, 增强对光谱可分性、 类别平衡性及模型复杂度等多目标的均衡搜索能力。 总之, INSGA-Ⅲ 改进后的初始化算法, 既有助于提升算法收敛速度与解集质量, 也更契合高光谱数据高维度、 多目标、 强物理约束的特性需求。
在LHS的候选解生成过程中, 对于维度为d的决策空间(波段组合维度), 生成N个候选解时, 每个维度xi的采样点应满足式(1)
式(1)中, k=1, 2, …, N; i=1, 2, …, d; π i表示第i维的一个随机排列函数, u~U(0, 1)为均匀分布的随机数。
关于参考点引导的个体筛选准则, 标空间中参考点zj的关联准则基于归一化目标向量与参考线的垂直距离如式(2)所示
式(2)中, zmin和zmax分别为当前种群中各目标的最小值与最大值, wj为参考点方向向量, f(x)代表个体的多目标值。
式(1)直接体现改进算法在决策空间(波段组合维度)的均匀探索能力, 是解决NSGA-Ⅲ 初始解分布稀疏问题的核心; 式(2)作为NSGA-Ⅲ 参考点引导机制的关键扩展, 定义了目标空间中解集的分布优化准则, 直接影响地物分类场景下帕累托前沿的物理可解释性。 二者分别从决策空间和目标空间角度优化初始化过程, 共同解决了高光谱波段选择中维度高、 目标冲突性强、 类别不平衡等挑战。
NSGA-Ⅲ 定义适应度函数的主要依据为非支配排序层数和参考点关联度, 适用于波段选择的多目标优化。 但由于未显式抑制波段冗余相关性且未引入分类精度驱动项, NSGA-Ⅲ 解集容易包含冗余波段并偏离分类性能优化, 降低地物识别准确性。 此外, 其参考点引导在高维目标空间易偏离地物可分性需求, 削弱解集的物理可解释性与分类鲁棒性, 制约其在高光谱地物分类中的实际效能。
在NSGA-Ⅲ 的基础上, INSGA-Ⅲ 在适应度函数中引入了基于ARF的分类精度驱动项和基于皮尔逊相关系数的波段间相关性惩罚项。 前者有助于增强目标空间梯度, 引导算法快速逼近全局帕累托前沿; 后者则负责约束局部搜索方向, 降低冗余波段干扰。 结合NSGA-Ⅲ 的参考点引导机制, INSGA-Ⅲ 的适应度函数能够更好地实现收敛速度与多样性的动态平衡: ARF缓解类别不平衡导致的早熟收敛, 相关性惩罚避免局部高相关解聚集, 使解集同时覆盖高分类精度、 低冗余及物理可解释的波段组合, 从而显著提升高光谱地物分类场景下多目标优化的综合性能。
基于ARF的分类精度驱动项如式(3)所示
$f_{\mathrm{ARF}}(x)=\frac{1}{K} \displaystyle\sum_{k=1}^{K} \operatorname{Acc}_{\mathrm{CV}}^{(k)}(x)$(3)
式(3)中, x为波段组合, K为ARF的基学习器数量, Ac
基于皮尔逊相关系数的波段间相关性惩罚项如式(4)所示
$f_{\mathrm{corr}}(x)=\lambda \displaystyle\sum_{i< j \in x}\left|\rho_{i j}\right|^{2}$(4)
式(4)中, ρ ij为波段i与j的皮尔逊相关系数, λ 为惩罚系数(通常设为0.1~0.5)。
NSGA-Ⅲ 的适应度函数并非通过显式数学公式计算, 而是通过多目标优化的非支配排序与参考点关联机制动态确定个体的适应度优先级。 在NSGA-Ⅲ 的适应度函数的基础上, INSGA-Ⅲ 的综合适应度函数如式(5)所示
式(5)中, 负号表示最小化相关言惩罚项。 fsize(x)=|x|为波段数量目标项, 表示最小化所选波段数量, 以此控制模型复杂度, 迫使算法选择信息量高且互补的波段组合, 避免冗余波段的无效堆砌。
上述公式中, 式(3)直接体现INSGA-Ⅲ 对地物分类性能的显式优化, 是区别于NSGA-Ⅲ 的核心改进; 式(4)解决高光谱数据波段间强相关性导致的冗余问题, 提升解集的物理意义; 式(5)定义多目标优化的整体框架, 明确各子目标的冲突关系与优化方向, 为算法提供可量化的评估基准。
NSGA-Ⅲ 依赖遗传算法的变异操作(如多项式变异)进行局部搜索, 但其随机扰动缺乏方向性, 且受支配关系单一判据制约, 难以定向优化分类精度敏感波段, 导致解集收敛至次优帕累托前沿, 分类精度提升缓慢, 且高光谱数据的高维特性加剧局部搜索效率低下问题, 延长收敛周期。
INSGA-Ⅲ 引入了PSO算法的速度与位置更新机制, 通过个体历史最优解与群体最优解引导变异方向, 结合动态惯性权重平衡算法的探索与开发强度。 该策略增强了对分类精度敏感波段邻域的定向搜索能力, 同时利用PSO的群体协同加速收敛, 弥补了传统变异操作的随机性缺陷, 能够显著提升地物分类精度与收敛速度, 适用于高维波段选择中复杂帕累托前沿的精细化搜索需求。
PSO是一种基于群体智能模型的优化算法, 通过模拟鸟群等群体的觅食行为寻找最优解。 该算法可生成一群粒子, 每个粒子都有自己的位置和速度, 位置代表一种可能的解, 速度代表解变化的方向和快慢。 在搜索空间飞行的过程中, 粒子在下一时刻的速度除了受惯性影响外, 还会根据个体认知(指向个体最优位置的速度分量)和社会认知(指向全局最优位置的速度分量)不断调整速度并移动到新位置。 PSO具有收敛速度较快、 参数少等优点, 广泛应用于函数优化、 神经网络训练等诸多领域。
在融合了PSO动态更新机制的局部搜索策略改进中, 核心数学模型包括了速度更新、 动态惯性权重及变异操作的协同机制。
PSO引导的变异速度更新公式如式(6)所示
式(6)中,
动态惯性权重衰减公式如式(7)所示
式(7)中, wmax为初始惯性权重(如0.9), 用于增强全局探索能力; wmin为最终惯性权重(如0.4), 用于强化局部开发精度; T为最大迭代次数, t为当前迭代次数。
PSO协同的离散变异操作公式如式(8)所示
式(8)中, Sign(vi)为速度方向函数, 取± 1决定波段增减方向; Bernoulli(p)为以概率p输出1的伯努利分布, p∈ [0, 1] 由速度幅值归一化得到; Mutation为传统变异, 按概率翻转波段选择状态。
上述公式中, 式(6)提供分类精度与低冗余的搜索方向, 奠定方向性搜索基础; 式(7)的动态权重与式(6)实现群体协同, 能够平衡探索与开发, 显著减少无效搜索; 式(8)将式(6) 的搜索方向映射至离散波段组合空间, 实现PSO与遗传变异的无缝融合, 使变异操作从“ 随机扰动” 升级为“ 目标导向的智能扰动” 。 三者协同解决了NSGA-Ⅲ 在高光谱波段选择中随机变异低效、 收敛方向模糊的缺陷, 为地物分类场景提供高精度、 低冗余的帕累托最优解集。
INSGA-Ⅲ 与NSGA-Ⅲ 的局部搜索策略对比如表2所示。
| 表2 INSGA-Ⅲ 与NSGA-Ⅲ 的局部搜索策略对比 Table 2 Comparison of local search strategies between INSGA-Ⅲ and NSGA-Ⅲ |
为了验证本算法(INSGA-Ⅲ )在多场景高光谱波段选择中是否具有普适性优势, 首先, 需要验证INSGA-Ⅲ 在农业、 城市、 植被及矿物等多类别场景中, 是否具备更优的信息保留与冗余控制能力; 其次, 需要验证INSGA-Ⅲ 在分类精度、 收敛速度及抗噪性上是否优于传统方法与主流多目标优化算法。 因此, 实验基于Indian Pines(农业场景)、 Pavia University(城市地物场景)、 Salinas(植被监测场景)及Botswana(矿物识别场景)四类高光谱数据集开展, 数据集的具体信息(名称、 场景、 波段数量、 空间分辨率和地物类别数量)及其预处理如表3所示。
| 表3 实验数据集及其预处理 Table 3 Experimental data set and its preprocessing |
实验选取广泛应用的顺序前向选择(SFS)、 竞争性自适应重加权采样(CARS)、 多目标粒子群优化(MOPSO)、 基于分解的多目标进化算法(MOEA/D)及原始NSGA-Ⅲ 算法作为基准算法, 用以验证INSGA-Ⅲ 的普适优势。 基准算法的类型、 核心参数设置与比较目的等相关信息如表4所示。 此外, 实验还对四类数据集进行了统一的标签划分(训练集70%, 测试集30%), 所有算法均在相同硬件环境(CPU: Intel i7-12700, RAM: 32GB)下运行。
| 表4 实验基准算法及其比较目的 Table 4 Experimental benchmark algorithms and their comparison purposes |
具体实验内容包括如下四部分:
(1)波段选择效果验证。 输入数据为四类数据集的全波段光谱数据。 首先分别运行SFS、 CARS、 MOPSO、 MOEA/D、 NSGA-Ⅲ 及INSGA-Ⅲ 算法进行波段选择, 然后记录各算法选择的波段数及运行时间。 评估指标则包括波段数占比(选择波段数/全波段数)和算法运行时间(秒), 前者用于衡量算法的冗余控制能力, 后者用于描述算法执行效率。
(2)分类性能对比。 输入数据为各算法选择的波段子集和对应的数据集标签。 首先使用SVM分类器(RBF核, 5折交叉验证)训练模型, 然后计算总体分类精度(overall accuracy, OA)和Kappa系数这两项评估指标。
(3)多目标优化能力分析。 输入数据为四类数据集的全波段光谱数据。 运行INSGA-Ⅲ 及基准算法, 记录其关于最佳指数因子(optimum index factor, OIF)与平均互信息(average mutual information, AMI)的帕累托前沿, 分析不同算法中OIF与AMI之间的权衡关系。
(4)抗噪性与鲁棒性测试。 输入数据为向四类数据集添加高斯噪声(SNR=15、 25 dB)后的含噪数据。 首先在含噪数据上重复实验(1)— 实验(3), 然后对比各算法在噪声环境下的性能衰减。 评估指标包括噪声鲁棒性(含噪数据OA/纯净数据OA)和分类精度标准差(基于30次重复实验)。
在显著性水平α =0.01下, 针对INSGA-Ⅲ 与每种基准算法分别进行双侧配对t检验, 并对多重比较结果采用Bonferroni 校正。 Indian Pines、 Pavia University、 Salinas及Botswana 四类高光谱数据集的实验结果如表5所示。 其中, 粗体代表对应数据集实验中该列参数的最优值, 下划线代表对应数据集实验中该列参数的次优值(其他表格设定相同)。
| 表5 高光谱数据集实验结果 Table 5 Experimental results for hyperspectral datasets |
由表5可知, INSGA-Ⅲ 的整体性能显著占优。 相对于基准算法相应指标的均值, INSGA-Ⅲ 关于OIF与AMI这两项指标的平均提升幅度分别为8.5%与9.7%, 波段数占比平均降低33.8%, 在SVM分类器中的OA与Kappa系数最高分别可达92.7%与0.913, 平均提升幅度则分别达到10.3%与11.6%。 此外, INSGA-Ⅲ 可在80次迭代收敛至稳定非支配解集, 收敛速度较NSGA-Ⅲ 提高约32%。
在四组高光谱数据集上, INSGA-Ⅲ 与基准算法关于OIF与AMI的二维帕累托前沿如图2所示。 根据图2中四组子图的二维帕累托前沿对比结果(需要特别指出的是, 为优化显示效果, 图中横坐标上的数值为左大右小), INSGA-Ⅲ 在高光谱波段选择的双目标优化中展现出显著优势: 其帕累托前沿在全部4组实验场景中均向二维坐标轴的右上方(AMI值小、 OIF值大的理想区域)充分延展, 解集覆盖范围也全部集中在坐标轴右上方区域, 形成较为连续、 完整的非支配解边界, 表明该算法能够有效实现“ 保留有效信息” 与“ 剔除冗余信息” 的双目标优化。 而尽管SFS和CARS的帕累托前沿的AMI指标略优于INSGA-Ⅲ , 但其OIF指标均远逊于INSGA-Ⅲ , 其余3种基准算法的帕累托前沿则全面落后于INSGA-Ⅲ , 说明相比5种基准算法, INSGA-Ⅲ 具有最优的帕累托前沿, 能够实现最优的信息-冗余双目标优化。
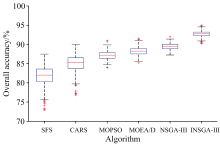
基于不含噪声的四类高光谱数据集, 使用t检验(p< 0.05)验证INSGA-Ⅲ 与5种基准算法的显著性差异, 得到的带有显著性标识的箱体图如图3所示。 可以看出, 与INSGA-Ⅲ 比较时, 各基准算法的p值均低于0.05, 表明差异均具有统计显著性, 其中SFS和CARS分别以0.000 1和0.000 3达到极显著水平, MOPSO的p值为0.001 9达到高度显著水平, 而MOEA-D和NSGA-Ⅲ 分别以0.014 3和0.038 7达到显著水平, 说明在实验指标上INSGA-Ⅲ 与所有对比算法之间的性能差异均不太可能由随机因素引起, 进一步验证了INSGA-Ⅲ 在改进算法性能方面的优势。
上述实验结果表明, 相对于SFS与NSGA-Ⅲ 等基准算法, INSGA-Ⅲ 在的跨场景适应性更强, 适用于农业、 城市、 植被及矿物识别等多领域, 且在信息保留、 冗余控制及分类精度间能够实现更优平衡。
为验证INSGA-Ⅲ 算法中三项核心改进(LHS初始化、 分类-冗余双目标适应度函数、 PSO协同搜索)的独立贡献, 构建三组对照算法: INSGA-Ⅲ -A, 移除LHS初始化机制(采用随机初始化替代拉丁超立方采样与参考点引导); INSGA-Ⅲ -B, 移除适应度函数中的分类精度驱动项与波段相关性惩罚项(保留原始NSGA-Ⅲ 的非支配排序与参考点关联度); INSGA-Ⅲ -C, 移除PSO局部搜索策略(仅保留遗传变异操作)。 消融实验过程中, 数据集、 硬件环境、 参数设置和采用的分类器均保持不变, 以确保结果可比性。
表6所示的消融实验结果表明: 移除LHS初始化导致运行时间增加39.7%(四数据集均值)、 OA降低3.65%(四数据集均值), 证明其规避随机初始化偏差的核心作用; 简化适应度函数使冗余度上升12.1%(四数据集均值)而OA仅下降2.18%(四数据集均值), 凸显相关性惩罚项抑制冗余、 ARF分类项优化目标梯度的互补优势; 取消PSO协同搜索造成OA降低3.08%(四数据集均值)且耗时增加35.0%(四数据集均值), 验证了其实现敏感波段定向优化的特殊价值。 以上三者协同, 共同支撑起算法的跨场景最优平衡。
| 表6 消融实验结果 Table 6 Ablation experimental results |
在四个数据集上, 分别加入均值为0、 方差为0.1的高斯噪声, 并在两种噪声水平(SNR为15和25 dB)下进行测试, 得到各算法的分类精度分布箱线图如图4所示。 由图4可知, INSGA-Ⅲ 算法在分类精度分布上展现出显著优势, 其中位数(约92.7%)显著高于其他算法(如NSGA-Ⅲ 的89.5%、 MOEA/D的88.2%), 且箱体高度(代表精度波动范围)最小, 表明其精度分布集中、 波动性低, 标准差仅为0.8%, 验证了其在噪声干扰下的强鲁棒性。 相比之下, 传统算法如SFS和CARS的箱体较宽(标准差分别为2和1.8), 中位数(82.4%和85.6%)偏低且存在较多离群值(高噪声下的异常低精度), 而异常低精度的离群值会拉低均值, 增大性能波动风险, 说明其抗噪能力弱、 稳定性不足。 此外, INSGA-Ⅲ 波段数占比(较NSGA-Ⅲ 降低33.8%)、 运行效率(较NSGA-Ⅲ 提速32%)及收敛速度(80次迭代)方面均优于基准算法, 进一步佐证了其在多场景高光谱数据中能够实现信息保留与分类精度的最优平衡, 具备跨场景适应性和工程实用性优势。
各算法的噪声鲁棒性与分类精度标准差如图5所示, 其中, 图5(a)为各算法的噪声鲁棒性, 描述了算法在噪声条件下维持其性能或准确度的能力; 图5(b)为各算法在噪声条件下基于30次重复实验的OA标准差, 由于算法的波动范围与标准差具有正相关性, 可借用标准差来描述算法在处理含噪数据时的分类精度波动范围和稳定性。
在SNR=25 dB条件下, INSGA-Ⅲ 的噪声鲁棒性达到96.84%, 且分类精度标准差仅为1.23%, 显示出在噪声干扰下的高稳定性和较小的性能衰减。 5种基准算法的噪声鲁棒性分别为88.95%、 89.68%、 91.96%、 97.47%和95.21%, 均值为92.65%; 其标准差分别为1.05%、 5.15%、 5.88%、 2.71%和3.97%, 均值为3.75%, 表明在中等强度噪声下(SNR=25 dB), 基准算法的总体性能在鲁棒性与稳定性上均弱于INSGA-Ⅲ 。
在更强噪声条件(SNR=15 dB)下, 所有算法的鲁棒性均进一步下降。 然而, INSGA-Ⅲ 依然取得了最高的鲁棒性(89.87%)和最低的标准差(1.79%), 表现出极强的抗噪性和稳定性。 相比之下, 5种基准算法的鲁棒性降至80.35%至86.27%之间, 标准差分布在4.13%至6.63%之间, 表明其与INSGA-Ⅲ 的性能差距进一步拉大。
上述结果表明, 相对于基准算法, INSGA-Ⅲ 在面对噪声干扰时能够更好地保持其原有的分类性能, 同时具有更优的稳定性和抗噪能力。 这一优势源于INSGA-Ⅲ 的优化机制能够更有效地抑制噪声对目标优化过程的干扰, 从而提升算法在复杂噪声环境下的稳健性。
提出并验证了一种面向高光谱波段选择的信息-冗余双目标优化改进算法(INSGA-Ⅲ ), 通过融合自适应旋转森林(ARF)并基于分类性能筛选初始解、 多维度抗噪评估体系及粒子群优化(PSO)协同搜索机制, 系统性解决了传统NSGA-Ⅲ 在初始种群质量低、 泛化能力不足及局部搜索效率弱等方面的局限。 结果表明, INSGA-Ⅲ 在四类高光谱场景中展现出显著优势: 其帕累托前沿在信息保留(OIF)与冗余控制(AMI)的权衡中始终逼近理想区域, 关键指标平均提升9.1%, 冗余度降低超30%, 分类精度最高达92.7%(Kappa=0.913); 算法可在80代内快速收敛至稳定解集, 且抗噪性能优异(噪声下精度波动± 1.23%), 显著优于现有方法。
当前研究聚焦于信息-冗余-分类精度的多目标协同优化, 但在高光谱数据的空谱联合特征挖掘及显著波段边缘增强方面仍有深化空间, 未来拟融合目标显著性增强算法, 通过显著图与显著波段的空谱融合机制进一步提升地物分类的精度与效率, 同时探索多模态优化框架下的动态权重分配策略, 以应对复杂环境监测与精准农业决策中的实时性需求。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|