试验样本选取山东泰开公司新制复合绝缘子硅橡胶试片, 表面状况完好颜色较为鲜艳。 将样品用无水乙醇表面擦拭干净, 放在50 ℃的烘箱中干燥24 h, 然后冷却至室温。 使用分析天平称取样品重量(精确到0.001 g)。 然后将样品完全浸没在恒温水浴箱中, 温度控制在30 ℃。 并每间隔3 h称一次重, 样品不重复使用, 称重前用滤纸将样品擦干。 样品的吸水率使用式(1)计算

M(t)=mt-m0m0×100%(1)

式(1)中: m_t为硅橡胶试片吸水的相对增重百分比; m_t为t时刻硅橡胶试片吸水后的质量; m₀为硅橡胶试片的干燥时的初始重量。

将称重后的样品分别标为类别1、 2、 3、 …、 20, 每类硅橡胶试片表面随机取15个点, 即为300个试验样本点, 硅橡胶试验样本如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 硅橡胶试验样本Fig.1 Silicone rubber test samples

试验采用海洋光学生产的NIR-QUEST小型傅里叶变换近红外光谱仪, 型号为512, 波长范围为900~1 700 nm。 水分子在NIR波段1 450和1 940 nm显示显著的吸收峰, 分别对应于O— H键的第一倍频和第二倍频振动, 这些峰可通过预处理与特征提取算法有效识别。 积分时间为100 ms。 由海洋光学生成的DH-2000光源发射装置, 氘灯和钨卤灯联合使用, 近红外检测平台及其接线图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 近红外光谱检测平台Fig.2 Near-infrared spectroscopy detection platform

1.3.1 支持向量机模型

采用支持向量机(SVM)可以解决数据的高维性、 非线性以及噪声干扰等问题, 为了进一步提高预测准确度和模型泛化能力^[22], 使用支持向量机(SVM)建立了硅橡胶试片吸水率检测模型。 支持向量回归作为支持向量机在回归领域的延伸, 其数学本质可表述为带约束的凸优化问题, 如式(1)所示。 该优化目标通过最小化权重向量的范数实现结构风险最小化, 同时引入成对松弛变量和, 以允许样本点突破误差容限, 约束条件见式(2)。

$\operatorname{Min} \frac{1}{2}\|w\|^{2}+c \displaystyle\sum_{i=1}^{n}\left(\zeta_{i}+\zeta_{i}^{*}\right), \zeta_{I}, \zeta_{i}^{*} \geqslant 0, i=1, \cdots, n$(2)

$\operatorname{Max} \displaystyle\sum_{i=1}^{n} y\left(a_{i}^{*}-a_{i}\right)-\varepsilon \displaystyle\sum_{i=1}^{n}\left(a_{i}^{*}+a_{i}\right)-\frac{1}{2} \displaystyle\sum_{I, j=1}^{n}\left(a_{i}^{*}-a_{i}\right)\left(a_{i}^{*}+a_{i}\right) x_{i}^{\mathrm{T}} x_{j}$(3)

式(2)和式(3)中, w为最小化权重向量, ζ _i和 ζi*为松弛变量, c为正则化参数, a_i和 ai*为拉格朗日乘子。

在优化模型中, 正则化参数作为惩罚系数, 调控模型复杂度与训练误差之间的平衡关系: 当c值过大时易导致过拟合, 而过小则可能引起欠拟合。 ε 定义为误差容限, 决定回归函数对噪声的容忍度。 原始优化问题可转化为由拉格朗日乘子 ai*和a_i的对偶形式。 为处理非线性回归问题, 采用径向基函数(radial basis function, RBF)核进行特征空间映射, 表达式如式(3)所示, 其通用SVM预测方程可表示为式(4) 形式。

K(x, xk)=exp(-γ‖xk-x‖2)(4)

$F(x)=\displaystyle\sum_{i=1}^{n}\left(a_{i}^{*}+a_{i}\right) K\left(x, x_{k}\right)+b$(5)

式(4)和式(5)中, K(x, x_k)为RBF核函数, γ 为核系数尺度, b为偏置项。

K(x, x_k)通过γ 调控样本在高维空间的分布结构: γ 值增大将增强局部样本响应, 但可能降低模型泛化能力。 偏置项b通过支持向量的均值计算获得。 通过网格搜索与交叉验证联合优化超参数组合(c, γ ), 以提升模型在复杂非线性系统中的预测精度。

1.3.2 冠豪猪优化算法

冠豪猪优化算法(crested porcupine optimizer, CPO)是由Mohamed Abdel-Basset等于2024年提出的一种新型元启发式算法, 其设计灵感源于冠豪猪(crested porcupine, CP)的多层次防御行为。 该算法通过模拟冠豪猪的四种防御策略, 包括视觉威慑、 噪声警告、 臭味标记及身体攻击这四种防御区域划分机制, 实现对复杂优化问题的高效求解。 其核心在于通过动态调整搜索策略与种群规模, 平衡全局探索与局部开发能力, 从而提升算法收敛速度与求解精度^[23]。

CPO将冠豪猪的防御行为映射为以下四个递进式区域: 当捕食者距离较远时, CP通过视觉威慑进行预警, 对应算法中全局范围的初步探索; 若捕食者突破区域A, CP将激活噪声警告, 对应算法中基于适应度评估的局部搜索; 当捕食者持续逼近时, CP释放刺激性气味以驱赶目标, 映射为算法中针对高潜力解邻域的精细勘探; 若前三层防御均失效, CP将发起身体攻击, 对应算法中通过精英个体引导的集中开发, 强制收敛至最优解^[24]。

CPO的搜索过程始于随机生成的初始种群

Xi=L+r·(U-L), i=1, 2, …, N'(6)

式(6)中, X_i为第i个候选解, L和U分别为搜索空间的下限与上限, r∈ [0, 1]为均匀分布的随机数, N'为初始种群规模。

为平衡收敛速度与物种多样性, CPO引入动态种群规模调整机制

N=Nmin+(N'-Nmin)×1-t%TmaxTTmaxT(7)

式(7)中, %为模运算符, T_max为最大函数评估次数, T为循环周期参数, t为当前评估次数, N_min为种群规模最小值。 该机制通过周期性缩减种群规模, 保留高适应度个体并剔除冗余解, 从而加速收敛的同时避免早熟现象。

采用冠豪猪优化算法对支持向量机进行优化。 选择SVM中的最优惩罚参数c和核函数参数。 CPO-SVM具体步骤如下:

(1)优化豪猪冠群的种群和参数: 设置豪猪冠群的位置和速度, 并设定相关参数;

(2)执行防御策略进行全局探索, 应用循环种群削减技术调整种群规模, 并将各段的光谱数据作为模型的输入;

(3)将当前种群中每个冠豪猪个体代入SVM中进行训练。 采用交叉验证计算该组参数下SVM模型的准确率作为该个体的适应度值;

(4)根据(3)中的适应度值是否达到最优, 更新冠豪猪的位置和速度;

(5)如果满足终止条件, 则算法终止; 如果不满足, 则返回步骤(3)。

1.3.3 回归性能评价

基于MATLAB2022a数学分析平台, 构建硅橡胶试片吸水率的偏最小二乘回归(PLSR)预测模型。 首先对实验样品进行划分, 按照8∶ 2的比例将样本划分为训练集和测试集, 通过PLSR算法建立定量预测模型。 构建了多维度交叉验证, 通过统计指标、 误差指标及稳定性指标的三重验证系统化解析模型的预测精度与工程实用性。 采用决定系数(R²)来表示光谱变量与吸水率的关联强度, 通过均方根误差(RMSE)来表示预测值分布离散度, 辅以均方误差(MSE)和平均绝对误差(MAE)分别表征误差离散特性与绝对偏差水平, 实现从数据拟合度到外推稳定性的全链条性能评估。 R²≤ 1, 当R²越接近1, 说明光谱数据与吸水率之间的相关性越强, 模型的解释能力越好。 RMSE越小, 说明预测值越接近真实值, 模型的精度越高。 优秀的预测模型的特点RMSE和MAE值低, 而R²值高, 其最优的R²值为1。

$\mathrm{RMSE} =\left(\frac{1}{n} \displaystyle\sum_{i=1}^{n}\left(y_{i}-f_{i}\right)^{2}\right)^{\frac{1}{2}} $(8)

$\mathrm{MAE} =\displaystyle\sum_{i=1}^{n}\left|y_{i}-f_{i}\right|$(9)

$R^{2}=\frac{\displaystyle\sum_{i=1}^{n}\left(y_{i}-f_{i}\right)^{2}}{\displaystyle\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}$(10)

式(8)— 式(10)中, y_i表示真实值, f_i是预测值, ${\bar{y}}$表示真实值的平均值, n为样本数量。

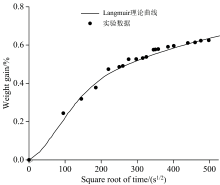
经典的Fick扩散模型仅考虑浓度梯度和热运动, 难以充分描述水分与高分子链之间通过氢键产生的吸附作用。 因此引入描述固体表面层吸附的Langmuir扩散模型以揭示硅橡胶中水分的非Fick扩散过程。 图3为硅橡胶试样在恒温水浴箱中浸泡时的重量增加曲线和Langmuir扩散模型的理论曲线。 同时可以看出, Langmuir扩散模型可以很好的描述试验结果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 硅橡胶试样随时间的吸水增重试验结果Fig.3 Test results of water absorption and weight gain of silicone rubber samples over time

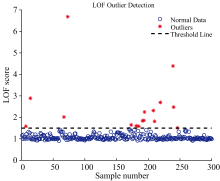
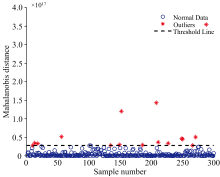
由于硅橡胶试片在数据采集过程中会存在漏光、 光源强度发生变化以及异常检测点干扰等因素产生异常数据, 这将对硅橡胶试片的含水量回归模型的预测性能、 鲁棒性与适用性产生较大地影响。 通过对原始数据进行异常样本剔除, 可以剔除掉因采样时环境干扰等原因产生的样本相关性弱的问题, 减少对后续实验的干扰并提升模型训练精度。 故分别使用局部异常因子算法(local outlier factor, LOF)和马氏距离算法(Mahalanobis distance, MA)对原始数据进行异常样本剔除。

由图4和图5可以看出, LOF剔除掉异常样本16条后剩余284条, MA剔除掉异常样本16条后剩余284条。 为了检验两种剔除算法的性能分别使用LOF和MA剔除异常值后的剩余数据建立PLSR模型并采取五折交叉验证的方式计算五折平均决定系数R²和RMSE指标。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于局部异常因子算法的异常检测结果Fig.4 Anomaly detection results based on the local anomaly factor algorithm

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 基于马氏距离的全局异常检测结果Fig.5 Global anomaly detection results based on Markov distance

根据表1结果可以看出, LOF算法进行异常值剔除后的数据建立的PLSR模型其五折平均决定系数R²更高, 这说明该算法提出异常样本后的数据能包含更多的信息模型更容易学习到其中的相关性。 因此后续实验将采用LOF剔除异常值后的数据进行。

表1

Table 1

表1(Table 1)

表1 LOF和MA剔除算法的性能 Table 1 The performance of LOF and MA elimination algorithms 方法 训练集 测试集 MSE RMSE MAE R2 MSE RMSE MAE R2 LOF 0.002 794 9 0.052 867 0.034 638 0.866 09 0.007 532 7 0.086 791 0.043 18 0.680 52 MA 0.002 608 6 0.051 074 0.030 337 0.855 99 0.005 329 8 0.073 005 0.050 066 0.646 77

表1 LOF和MA剔除算法的性能 Table 1 The performance of LOF and MA elimination algorithms

不同吸水率硅橡胶试片原始光谱如图6所示, 采用5种方法对硅橡胶试片样品的原始光谱图进行预处理, 包括MSC、 SNV、 SG、 一阶导数、 二阶导数。 预测精度和性能参数用于评估模型的质量, 不同预处理后的数据建立的PLSR模型其性能如表2所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
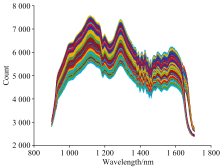	图6 不同吸水率硅橡胶试片原始光谱Fig.6 Original spectra of silicone rubber test sheets with different water absorption rates

表2

Table 2

表2(Table 2)

表2 基于不同光谱预处理硅橡胶试片吸水率预测模型结果 Table 2 Based on the results of the moisture content prediction model for composite insulators pretreated with different spectra 方法 训练集 测试集 MSE RMSE MAE R2 MSE RMSE MAE R2 MSC 0.002 794 9 0.052 867 0.034 638 0.866 09 0.007 532 7 0.086 791 0.043 18 0.680 52 SNV 0.002 608 6 0.051 074 0.030 337 0.855 99 0.005 329 8 0.073 005 0.050 066 0.839 13 SG 0.003 656 7 0.060 47 0.037 469 0.807 85 0.004 970 4 0.070 501 0.043 432 0.834 89 D1 0.002 145 6 0.046 32 0.036 087 0.907 21 0.007 132 2 0.084 452 0.064 832 0.505 93 D2 0.002 307 0.048 032 0.037 119 0.889 37 0.011 428 0.106 9 0.067 219 0.515 4

表2 基于不同光谱预处理硅橡胶试片吸水率预测模型结果 Table 2 Based on the results of the moisture content prediction model for composite insulators pretreated with different spectra

结果显示, 实验发现光谱数据经一、 二阶导数D1, D2预处理后建模效果变差, 可能是因为求导运算在突出信号变化时将噪声同步放大了, 噪声会干扰了模型训练; 导数算法虽能突出部分特征, 但会丢失宽峰等原始重要信息, 改变数据相关性, 让模型效果变差; 同时, 导数处理后数据细节与波动增多, 模型过拟合, 泛化能力差。

光谱原始数据经SNV处理效果好, 说明原始数据存在因样品物理性质差异等导致的乘性干扰和基线漂移问题。 这种干扰具有系统性但又因样品而异的特点, 可能源于样品颗粒大小、 堆积密度的差异, 或者测量过程中光路变化等。 这些因素会使光谱数据在不同样品间产生幅度和基线的不一致。 在光谱数据中, 乘性干扰和基线漂移表现为不同样品光谱的整体强度变化趋势不同以及基线的上下波动, 表现为原始光谱曲线在不同样品间呈现出强度比例失调且基线参差不齐, 而SNV能够通过对每个光谱进行标准化, 将其转化为具有单位标准差和零均值的形式, 从而有效消除这种因样品物理性质差异引起的乘性干扰和基线漂移, 提高数据的可比性和一致性, 提升数据质量^{[25, 26]}。

SNV预处理后的数据建立的PLSR其测试集决定系数R²最高达到0.839 13, 且五折交叉验证平均R²达到0.814 87, 这说明SNV数据能够消除较多的异常干扰, 让数据相关性更容易被模型捕捉到, 面对SNV预处理的数据上建立的模型效果最佳且泛化能力最强, SNV最适用于不同含水量硅橡胶试片样品, 如图7所示的SNV是数据预处理近红外光谱分析结果表明, 经过预处理后, SNV修正了大量原始复杂的光谱曲线基线漂移, 噪声干扰降低, 这种谱图质量的改善为后续的定量分析奠定了良好的基础。

图7

Fig.7

	Figure Option ViewDownloadNew Window
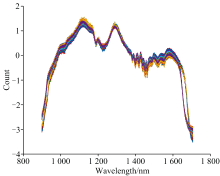	图7 不同吸水率硅橡胶试片SNV预处理光谱Fig.7 SNV pretreated spectra of silicone rubber test sheets with different water absorption rates

为了进一步提高预测准确度和模型泛化能力, 分别建立三种机器学习模型随机森林(random forest, RF)、 极限学习机(extreme learning machine, ELM)和支持向量机(SVM), 指标如表3。

表3

Table 3

表3(Table 3)

表3 基于SNV分别建立RF、 ELM、 SVM模型的结果 Table 3 The results of establishing RF, ELM and SVM models respectively based on SNV 方法 训练集 测试集 MSE RMSE MAE R2 MSE RMSE MAE R2 RF 0.001 065 8 0.032 647 0.015 671 0.953 08 0.003 046 5 0.055 195 0.035 616 0.811 83 ELM 0.003 043 7 0.055 17 0.035 208 0.859 93 0.003 339 6 0.057 789 0.042 469 0.833 02 SVM 0.000 057 516 0.007 583 9 0.007 327 9 0.997 38 0.001 788 5 0.042 291 0.026 331 0.905 96

表3 基于SNV分别建立RF、 ELM、 SVM模型的结果 Table 3 The results of establishing RF, ELM and SVM models respectively based on SNV

在标准正态变量变换(SNV)预处理的光谱数据集上, SVM展现出显著优于RF和ELM的建模性能。 SVM通过核函数映射技术将原始特征空间转换到高维希尔伯特空间, 在这个空间内构建具有最大几何间隔的最优分离超平面, 这种特性使其在处理本研究中复杂非线性光谱数据时表现出独特优势。 SVM的结构风险最小化原则使其对数据中的异常值具有较强鲁棒性, 同时通过调整惩罚参数c和核函数参数可有效平衡模型复杂度与泛化能力; 相比RF作为基于Bootstrap聚合的决策树集成模型, 尽管通过特征随机选择降低了单棵决策树的过拟合风险, 但面对本数据集高度非线性且存在多重共线性的光谱特征时, 其分段常数预测特性导致模型灵活性不足, 且当树深参数设置不当时容易产生过拟合现象; ELM凭借随机生成的输入层权重和Moore-Penrose广义逆矩阵解析解训练速度得到很好的提升, 但是其隐含层节点参数的随机初始化机制导致模型稳定性欠佳, 另外缺少有效的正则化约束, 在应对本回归任务中复杂的特征— 浓度映射关系时, 表现出明显的预测偏差和泛化能力的平衡上远不如SVM, 导致其在该回归问题中的表现不如SVM。

2.4.1 竞争性自适应重加权算法

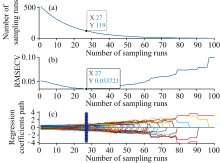
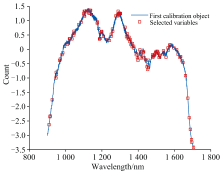
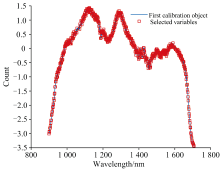
竞争性自适应重加权(CARS)算法的蒙特卡洛采样次数设定为100次, 采用5折交叉验证提取特征波长, 图8所示的是CARS算法提取特征波长过程。 图8(a)表明CARS提取的特征波长数量随采样次数增加呈现先急剧下降后平缓减少的趋势, 体现了特征波长由粗选到精选的过程; 图8(b)显示迭代初期由于无用信息波段被剔除, 交叉验证均方根误差(RMSECV)快速下降, 当采样次数达到27次时RMSECV达到最小值, 随后由于部分有用信息被剔除, RMSECV呈现整体上升趋势; 图8(c)表明在第27次采样时RMSECV值最小, 此时共提取出119个特征波长如图9所示。 结果表明CARS能筛选出高质量特征, 有效去除冗余和噪声。 CARS过程本身就会剔除那些与吸水率相关性不高的波长点, 这在一定程度上也削弱了表面界面氧化的影响。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 CARS算法提取特征波长过程 (a): 波长变量数目变化图; (b): RMSECV变化图; (c): 回归系数路径图Fig.8 The process of extracting characteristic wavelengths by the CARS algorithm (a): Graph of the number of wavelength variables; (b): RMSECV variation graph; (c): Regression coefficient path diagram

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 CARS提取特征波段Fig.9 CARS extracts feature bands

2.4.2 区间组合优化算法

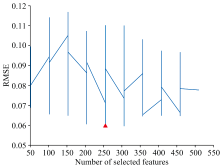
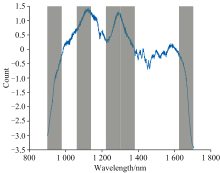
区间组合优化(ICO)算法基于光谱数据的局部特征差异, 将整个光谱区间划分为多个子区间, 每个子区间包含一定数量的连续波段。 通过对不同区间组合的分析和评估, 筛选出对目标分析物具有高相关性和低冗余性的区间组合, 从而实现光谱数据的降维和关键信息的提取。 区间组合优化算法的过程和结果如图10和图11所示, 图11中灰色标注区域即为筛选得到的特征波长区间。 图10数据表明, ICO降维后保留255个特征, RMSE降至0.06的最小值, ICO作为区间优化算法, 过于侧重区间优化, 保留的255个特征存在信息冗余, 无法很好突出与目标强相关特征, 影响数据对模型的支持效果。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 ICO提取特征波长过程Fig.10 The process of extracting characteristic wavelengths through ICO

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 ICO提取特征波段Fig.11 ICO extracts characteristic bands

2.4.3 连续投影算法

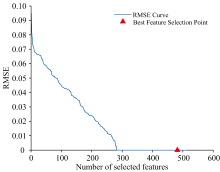
连续投影(SPA)算法的过程和结果如图12和图13所示, 数据表明, 随着特征波段数量的逐步增加, RMSE值呈现匀速下降的变化趋势, 最终确定的特征波段数量为482个。 图中橙色标注区域即为筛选得到的特征波段位置。 SPA降维后保留482个特征, 数量过多, 引入大量弱相关特征, 增大数据稀疏性与噪声影响, 未能有效提取有价值信息, 导致测试集效果不如未降维前数据。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 SPA提取特征波长过程Fig.12 The process of extracting characteristic wavelengths by SPA

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 SPA提取特征波段Fig.13 SPA extracts characteristic bands

基于不同特征提取算法的近红外光谱硅橡胶试片吸水率预测模型的比较如表4所示。 以测试集R²作为特征波段筛选效果的评价指标, 最后通过系统优化确定最佳波段数量。 采用三种算法特征提取后的数据再次建立SVM模型中, CARS降维后数据测试集R²达到0.888 08, CARS降维后的数据建立的SVM模型相对效果最好, 泛化性能也最高。

表4

Table 4

表4(Table 4)

表4 基于不同特征提取算法的近红外光谱硅橡胶试片吸水率预测模型的比较 Table 4 Comparison of Water Absorption rate prediction models for near-infrared spectral silicone rubber test sheets based on different feature extraction algorithms 方法 训练集 测试集 MSE RMSE MAE R2 MSE RMSE MAE R2 CARS 0.000 310 32 0.017 616 0.012 85 0.986 55 0.001 642 5 0.040 528 0.032 578 0.888 08 ICO 5.732 4× 10-5 0.007 571 3 0.007 352 8 0.997 52 0.003 409 7 0.058 393 0.038 547 0.764 82 SPA 5.067 2× 10-5 0.007 118 4 0.006 862 7 0.997 54 0.003 259 9 0.057 096 0.037 343 0.866 52

表4 基于不同特征提取算法的近红外光谱硅橡胶试片吸水率预测模型的比较 Table 4 Comparison of Water Absorption rate prediction models for near-infrared spectral silicone rubber test sheets based on different feature extraction algorithms

为了进一步提高模型的性能和预测精度, 基于SNV-CARS处理的数据建立SVM模型, 并对SVM模型引入不同优化算法对惩罚系数以及核函数参数γ 展开优化, 实验采用五折交叉验证方法, 通过决定系数R²、 均方根误差等指标全面评估模型性能。 基于不同优化算法的硅橡胶试片吸水率预测模型的比较如表5所示。

表5

Table 5

表5(Table 5)

表5 基于不同优化算法的硅橡胶试片吸水率预测模型的比较 Table 5 Comparison of water absorption rate prediction models of silicone rubber test sheets based on different optimization algorithms 方法 惩罚因子 (c) 核函数 尺度(γ ) 训练集 测试集 MSE RMSE MAE R2 MSE RMSE MAE R2 PSO-SVM 51.762 8 9.107 7 0.000 422 26 0.020 549 0.013 171 0.979 72 0.001 127 0.033 571 0.026 767 0.952 58 GWO-SVM 58.219 7 4.392 5 0.000 364 91 0.019 103 0.012 865 0.983 8 0.001 118 6 0.033 445 0.025 154 0.960 94 CPO-SVM 108.483 9 8.037 8 0.000 364 18 0.019 083 0.012 781 0.982 25 0.000 828 26 0.028 779 0.023 949 0.966 39

表5 基于不同优化算法的硅橡胶试片吸水率预测模型的比较 Table 5 Comparison of water absorption rate prediction models of silicone rubber test sheets based on different optimization algorithms

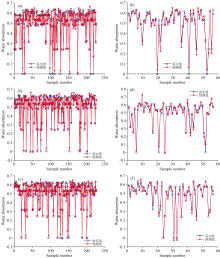
结果显示, CPO-SVM模型展现出显著优势, 如图14(e)和(f)所示, 在训练集和测试集上的决定系数分别达到0.982 55 和0.966 39, 五折交叉验证平均决定系数R²为0.948 6, 较PSO和GWO优化模型提升2.65%和3.68%。 这表明CPO算法不仅具有优异的参数优化能力, 还能有效提升模型的泛化性能。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 硅橡胶试片吸水率三种模型仿真图的对比 (a): PSO训练集; (b): PSO测试集; (c): GWO训练集; (d): GWO测试集; (e): CPO训练集; (f): CPO测试集Fig.14 Comparison of three Model simulation diagrams of Water Absorption rate of silicone rubber test sheets (a): PSO training set; (b): PSO test set; (c): GWO training set; (d): GWO test set; (e): CPO training set; (f): CPO test set

CPO之所以表现更优, 分析认为是其搜索机制在探索与利用间平衡良好, 前期能大步长全局搜索解空间, 后期则小步长局部微调, 有效避免陷入局部最优, 精准定位最优参数。 同时, CPO确定的参数能更好的平衡模型偏差与方差, 使用较大惩罚因子控制训练误差, 寻优得到的核函数参数能够更有效增强数据线性可分性。 此外, CPO搜索特性契合实验数据复杂分布, 充分挖掘潜在信息, 而PSO和GWO对于本实验具有算法局限性, 致使模型性能不如CPO优化的SVM。