选取中国河北省石家庄市、 四川成都市耕地为研究对象, 开展耕层土壤有机质含量检测的研究, 土样采集时间为2020年10月12日至16日。 共采集161个土样, 选取面积大于10亩且平坦的地块, 采用5点混合法采集土样, 取样深度为耕层20 cm。 待取样完成后, 将土样置于暗室内自然风干, 然后对土样进行研磨、 过筛(20目)处理。 将处理完成的土壤分为2份, 一份用于土壤有机质含量的检测, 一份用于室内土壤光谱的测定, 有机质含量的测定方法为重铬酸钾滴定法。 土壤有机质含量的基础统计参量如表1所示。

表1

Table 1

表1(Table 1)

表1 土样土壤有机质含量信息统计表 Table 1 Statistics of soil organic matter content in soil samples 指标 数量 最大值 /% 最小值 /% 平均值 /% 标准差 /% SOM 161 8.97 0.449 2.867 1.213

表1 土样土壤有机质含量信息统计表 Table 1 Statistics of soil organic matter content in soil samples

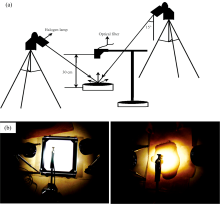
选用美国ASD公司生产的便携式地物光谱仪, 该光谱仪可测350~2 500 nm区间的地物光谱, 输出的光谱分辨率为1 nm。 实验在暗室内进行, 先将待测土样置于器皿内, 土壤厚度大于2 cm; 光源采用1 000 W的卤光灯提供平行光, 光线入射角为15° , 光纤置于土壤上方30 cm 处; 土壤光谱测定时, 先采用标准白板进行定标, 然后再采集土样光谱, 每个土样采集10条光谱, 取其均值作为最终光谱。 受地物光谱仪内暗电流、 室内环境等因素的影响, 测定的土壤光谱数据内含有一定噪声信息, 为减弱噪声信息的干扰, 提高土壤光谱数据的信噪比, 选用海明窗低通滤波器对土壤光谱进行去噪处理。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 室内土壤光谱测定示意图(a)与现场图(b)Fig.1 Schematic diagram of indoor soil spectral measurement (a) and experiment scene (b)

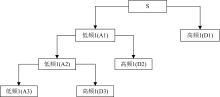
离散小波算法是一种重要的光谱数据处理与分析算法, 该算法可将光谱信息分解为不同尺度的低频、 高频信息, 从而有助于可用光谱信息的分离。 截止目前大多研究仅将离散小波算法用于光谱信息的分离, 而少见将离散小波算法应用于光谱信息耦合。 为探寻利用离散小波算法进行光谱信息耦合的可行性, 并为有效光谱信息的耦合提供一种新方法, 本研究先利用离散小波算法对光谱信息进行分离, 然后再对分离后的光谱信息进行耦合。 选用Coif2、 db5、 meyer、 rbio3.7、 sym2等5类小波作为小波基, 分解尺度为10。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 离散小波算法处理光谱数据的流程Fig.2 The flow of discrete wavelet algorithm for processing spectral data

其中, S为土壤光谱数据; D_i是基于离散小波算法分离的i分解尺度的高频信息; A_i是基于离散小波变换分离的i分解尺度的低频信息。

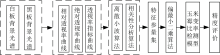
为提升光谱对土壤有机质含量的敏感性, 提高光谱对土壤有机质含量的估测能力, 提出了一种光谱数据分离、 耦合算法: 先利用离散小波算法、 相关性分析算法计算各尺度高频信息与土壤有机质实测值的相关系数; 然后利用相关系数计算耦合系数, 并利用耦合系数重构土壤光谱数据; 最后利用离散小波算法处理分析重构的土壤光谱数据, 并结合相关性分析算法、 建模算法构建土壤有机质含量估测模型。 本研究的技术路线图如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 光谱数据耦合的技术路线Fig.3 Technical route for spectral data coupling

利用光谱处理技术可从光谱数据内提取可用光谱信息, 且每种处理方法均能获取原光谱内含的不同信息, 基于特定处理方法提取的光谱信息均可视为原光谱在某一维度的信息表达。 当利用不同方法分别提取原光谱内的有效信息时, 可将各有效信息视为多个维度的光谱信息; 若不同维度的光谱信息间的相关性较弱且敏感波段的波段位置存在差异, 则不同维度的光谱信息间存在较强的互补性, 因而耦合不同维度的光谱信息对于提升光谱对地物参量的敏感性具有重大意义, 且可为光谱技术的应用推广提供基础技术支撑。

在深入分析各小波基对光谱信息分离的影响的基础上, 提出了一种基于离散小波算法的WYC数据耦合算法。 该算法先以db5、 sym2、 ribo3.7、 dmey、 coif2为小波基分别对土壤光谱数据进行处理, 分别得到1~10分解尺度的高频信息、 低频信息。 由于已有研究表明低频信息在提升光谱对土壤有机质含量的敏感性方面较弱, 因而选用各小波基分离的高频信息作为耦合对象。

首先基于各小波基对土壤光谱数据进行分离, 提取高频信息, 并采用相关性分析算法定量分析各高频信息与土壤有机质含量的相关系数。 然后利用高频信息与土壤有机质含量的相关系数生成耦合系数。 最后, 依据耦合系数生成耦合光谱信息, 具体计算方法如式(1)— 式(7)。

(1)相关性分析算法计算公式如式(1)

$\operatorname{cor}_{j}=\frac{\displaystyle\sum_{i=1}^{n}\left(X_{i}-X_{A}\right) *\left(Y_{i}-Y_{A}\right)}{\sqrt{\displaystyle\sum_{i=1}^{n}\left(X_{i}-X_{A}\right)} * \sqrt{\displaystyle\sum_{i=1}^{n}\left(Y_{i}-Y_{A}\right)}}$(1)

式(1)中, cor_j为相关系数, X_i为位于j波段第i个样本的光谱信息, Y_i为样本测定的参量, n为样本的总数; X_A为位于j波段的所有样本光谱信息的平均值, Y_A为位于j波段的所有样本参量的平均值。

(2)耦合系数的计算法方法如式(2)— 式(5)

cormax_j=max(corj)(2)

cormax=[cormax_1, cormax_2, …, cormax_n](3)

cormax_all=max(cormax)(4)

$\operatorname{coe} f_{\mathrm{j}}=\frac{\operatorname{cor}_{~max\text {_j }}~~~}{\operatorname{cor}_{~max\text {_all }}~~~}$(5)

式(2)— 式(5)中, cor_{max_j}为第j变换方法的最大相关系数(或基于小波分解的第j尺度的最大相关系数); cor_max为基于各变换算法的最大相关系数构建的数据集合; cor_{max_all}为全部变换算法的最大相关系数; coef_j为第j变换算法的聚合系数; max为求向量数组最大值的函数, 可采用matlab、 C、 C++等语言实现。

(3)基于不同小波基分解后, 各小波基分解信息的耦合公式如式(6)

$S_{\mathrm{wb}_{-} c}=\displaystyle\sum_{n}^{1} S W_{\mathrm{wb}_{-} j} * \operatorname{coef}_{\mathrm{wb}_{-} j}$(6)

式(6)中, S_{wb_c}为采用同一小波基分解后, 各分解尺度信息的耦合结果; SW_{wb_j}为采用wb小波基分解后的第j尺度信息; coef_{wb_j}为采用wb小波基分解后的第j尺度信息的耦合系数; n为分解尺度。

$S_{c_{-} \mathrm{all}}=\displaystyle\sum_{m}^{1} S W_{\mathrm{wb}_{-} c} * \operatorname{coef}_{\mathrm{wb}_{-} c}$(7)

式(7)中, S_{wb_all}为各小波基的耦合结果; S_{wb_c}为采用wb小波基分解后, 各分解尺度信息的耦合结果; coef_{wb_c}为采用wb小波基分解后, 各分解尺度信息的耦合结果的耦合系数; m为采用的小波基个数。

偏最小二乘法是一种传统回归算法, 该算法集主成分分析、 多元回归分析、 相关分析的优点于一体, 主要通过使误差的平方和最小而找到最优估测模型参量。 该方法能够有效避免多变量间的共线问题, 提升模型的估测精度, 是常用的多元线性回归算法。 截至目前, 该算法已广泛应用于地表土壤参量、 植被理化参量的估测^[16]。

随机森林(random forest)是一类机器学习算法, 该算法是基于决策树采用bagging方式进行集成的一种回归算法。 随机森林算法是通过并行多个决策树对数据进行处理, 且每棵决策树相互独立。 由于每棵树互不干扰, 且采用的样本是随机的, 因此, 每棵树预测的值也不同。 随机森林的预测结果是多棵树预测结果的均值^[17]。

为了客观评价耦合前、 后, 光谱对土壤有机质含量的敏感性与估测能力, 选用决定系数(R²)为评价指标, 对比分析耦合前、 后光谱对土壤有机质含量的敏感性。 选用R²、 RMSE评价耦合前、 后光谱对土壤有机质含量的估测能力, R²与RMSE的计算方法如式(8)和式(9)所示。

$R^{2}=1-\frac{\displaystyle\sum_{i=0}^{n}\left(\mathrm{SOM}_{i}-\mathrm{SOMP}_{i}\right)^{2}}{\displaystyle\sum_{i=0}^{n}\left(\mathrm{SOM}_{i}-\overline{\mathrm{SOM}_{i}}\right)^{2}}$(8)

$\operatorname{RMSE}=\sqrt{\frac{\displaystyle\sum_{i=1}^{n}\left(\mathrm{SOM}_{i}-\mathrm{SOMP}_{i}\right)^{2}}{n}}$(9)

式(8)和式(9)中, SOM为野外实地采集样本土壤有机质的实测值, SOMP为基于估测模型土壤有机质的预测值, SOM_i为土壤有机质含量的均值。

为更好的客观地检验土壤有机质含量估测模型的精度, 将样本分为建模组、 验证组, 其中建模组约占2/3(107个), 验证组约占1/3(54个)。 为分析建模组、 验证组样本的分布情况, 依据土壤有机质含量0.5 g· kg^-1的间隔, 统计建模组、 验证组土样样本的分布, 其分布情况如图4所示。 图4左图为建模组样本, 图4右图为验证组样本。 从图4可知, 土壤样本的分布整体呈正态分布, 符合土壤有机含量估测模型构建与验证的基本要求。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 土样土壤有机质含量统计图Fig.4 Statistical chart of soil organic matter content in soil sample

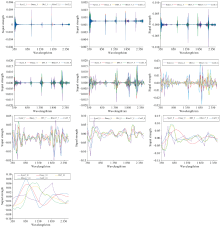
为便于分析小波基的选择对各尺度分解信息的影响, 将基于Coif2、 Db5、 Meyer、 Rbio3.7、 Sym2小波基分解的光谱信息按尺度作图, 并进行对比分析。 图5为原光谱经离散小波分解后各尺度信息的分布图, 其中图5(a)— (j)依次为各小波基1尺度至10尺度的分解信息汇总图。 由图5可知, 从1~10尺度开展对比分析可知, 采用不同小波基分离的光谱信息在几何形态上存在明显差异, 且该差异随尺度的增加而逐步增强, 其中小波基的选择对低尺度信息(1~3尺度)形态的影响相对较弱, 而对高尺度(4~10尺度)信息的几何形态的影响明显较强。 从6~10尺度分离的信息进行对比分析可知, 基于小波基分离的信息在几何形态上存在较大差异, 这表明利用各小波基分解的信息内涵的信息不同。 综上可知, 不同小波基分离的信号在几何形态(包含的信息)方面存在明显差异, 这为基于离散小波算法光谱信息的耦合提供了基础理论支撑。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 基于5类小波基分离的1~10尺度高频信息图Fig.5 1~10 scale HF infographics based on 5 classes of wavelet basis separation

由于采用不同小波基分离的光谱信息间存在较大差异, 尤其在细节信息方面, 因此基于不同小波基分离的光谱信息具有较强的互补性。 为耦合不同小波基分离的光谱信息, 分离、 凸显土壤光谱内的可用信息, 本研究采用WYC耦合算法, 将5类小波基分离的光谱信息进行耦合, 并再采用离散小波算法进行处理, 小波基为dmey, 分解尺度为10尺度。

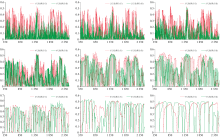
图6为1~10尺度耦合前、 后的光谱信息与土壤有机质含量的R²曲线图, 其中红线为耦合后, 绿线为耦合前。 从图6 可知, 在1~3尺度内, 耦合后的光谱信息能明显提升光谱对土壤有机质含量的敏感性; 耦合后, 光谱对土壤有机质含量敏感的波段数量明显增加, 且在350~2 500 nm区间的分布较好。 在4~6尺度内, 耦合后的光谱信息在局部能明显提升光谱对土壤有机质含量的敏感性, 且能弥补耦合前光谱在局部敏感性的不足。 在7~9尺度内, 耦合前、 后光谱对土壤有机质含量的敏感性无明显增强或减弱。 在10尺度, 耦合后光谱对土壤有机质含量的敏感性明显高于耦合前。 与耦合前相比, 在1~10尺度内, 耦合后光谱与土壤有机质含量的R²平均提升了15.33%, 其R²最高可达0.588。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 1~10尺度耦合前、 后与土壤有机质含量的R2Fig.6 Values of R2 before and after 1~10 scale coupling for soil organic matter content

为便于分析耦合前、 后, 光谱对土壤有机质含量的估测能力, 先利用离散小波算法分别对原光谱与耦合后的光谱进行处理分析, 小波基分别为Coif2、 Db5、 Meyer、 Rbio3.7、 Sym2, 每个小波基的分解尺度均为10。 然后, 分别采用偏最小二乘算法、 随机森林算法逐尺度构建土壤有机质含量估测模型; 最后, 采用R²、 RMSE对各模型进行评价。 本研究共构建了200个模型, 模型数量较多, 为便于分析, 本研究将耦合前、 后构建的模型进行编号, 具体情况如表2所示。 耦合前、 后各模型评价指标的分布图如图7、 图8所示。

表2

Table 2

表2(Table 2)

表2 模型编号与建模信息列表 Table 2 Model number and modeling information list 序号 小波基 尺度 波段 序号 小波基 尺度 波段 1 Coif2 D1 1 413 188 1 31 rbio3.7 D1 1 413 188 1 2 D2 399 142 4 32 D2 433 141 1 3 D3 794 140 7 33 D3 1 400 221 6 4 D4 550 143 6 34 D4 494 140 3 5 D5 630 740 35 D5 1 367 223 2 6 D6 474 152 0 36 D6 1 926 205 5 7 D7 374 191 3 37 D7 621 161 2 8 D8 884 123 0 38 D8 705 200 1 9 D9 399 250 0 39 D9 511 766 10 D10 510 129 6 40 D10 878 250 0 11 db5 D1 1 413 220 6 41 sym2 D1 4 97 141 6 12 D2 433 142 4 42 D2 1 366 191 1 13 D3 628 142 1 43 D3 619 141 3 14 D4 1 403 44 D4 859 140 1 15 D5 1 395 146 1 45 D5 1 890 226 1 16 D6 2 180 225 4 46 D6 471 212 3 17 D7 807 204 9 47 D7 434 171 1 18 D8 713 161 0 48 D8 515 145 5 19 D9 800 49 D9 400 885 20 D10 897 250 0 50 D10 365 205 3 21 meyer D1 1 413 187 8 22 D2 1 016 141 1 23 D3 1 435 220 3 24 D4 491 140 1 25 D5 1 391 223 0 26 D6 1 937 220 9 27 D7 826 236 0 28 D8 1 928 210 6 29 D9 436 200 0 30 D10 350 148 8

表2 模型编号与建模信息列表 Table 2 Model number and modeling information list

图7

Fig.7

	Figure Option ViewDownloadNew Window
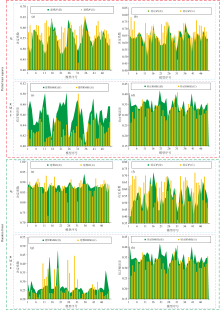	图7 耦合前、 后各模型评价指标R2、 RMSE的曲线图Fig.7 Curves of evaluation indexes of each model before and after coupling

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 最优模型实测值与估测值的散点图Fig.8 Scatter plot of actual values and estimated values of the optimal model

图7为耦合前、 后基于偏最小二乘算法、 随机森林算法构建的土壤有机质含量估测模型, 共计200个。 图7(a)— (d)采用的建模算法为偏最小二乘算法, 图7(e)— (h)采用的建模算法为随机森林算法。 图7(a)、 (b)、 (e)、 (f)为耦合前(绿色)、 耦合后(黄色)各模型建模与验证样本的R²分布图, 图7(c)、 (d)、 (g)、 (h)为耦合前(绿色)、 耦合后(黄色)各模型建模与验证样本的RMSE分布图。

由图7(a)— (h)进行对比分析可知: (1)与耦合前模型相比, 耦合后模型的评价指标R²整体均明显高于耦合前, 模型的评价指标RMSE显著降低, 这表明本研究提出的耦合方法能有效提升模型对土壤有机质含量的估测精度, 降低模型的估测误差。 (2)小波基的选择对耦合前、 后模型的建模与验证样本的R²、 RMSE均具有重要影响, 其中以小波基Coif2、 Sym相对较好, 由二者分离的光谱信息构建的模型的稳定性更好、 精度更高; 此外, 分解尺度也对模型的精度具有重要影响, 模型的评价指标R²整体随尺度的增加而呈先增加后降低的趋势, 相应模型的RMSE也随尺度的增加而呈先降低后升高的趋势, 每个小波基内最优估测模型多分布于1~5尺度内。 (4)从建模算法角度分析, 基于随机森林算法构建的估测模型的建模精度明显高于偏最小二乘算法, 但模型的验证精度却低于偏最小二乘算法, 这表明偏最小二算法在本研究中的表现相对较好, 究其原因是随机森林算法拥有较强的拟合能力, 因此其训练精度一般较高。 (5)将利用偏最小二乘算法构建的耦合前、 后的50个模型的评价指标取均值可知, 与耦合前相比, 耦合后基于偏最小二乘算法构建的模型的验证精度的R²平均提升了6.28%, RMSE平均降低了6.09%, 其最优模型(序号43)的验证精度的R²=0.760, RMSE=0.281%。 将基于随机森林算法构建的耦合前、 后的50个模型的评价指标取均值可知, 与耦合前相比, 模型的验证精度的R²平均提升了10.69%, RMSE平均降低了4.82%, 其最优模型(序号42)的验证精度的R²=0.719, RMSE=0.230%。 与耦合前相比, 耦合后全部模型的验证精度的R²平均提升了8.31%, RMSE平均降低了5.41%, 其最优模型为利用随机森林算构建— 序号为42的模型, 其验证精度的R²=0.719, RMSE=0.230%。

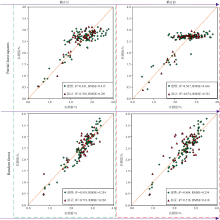
图8为耦合后利用偏最小二乘算法、 随机森林算法分别构建的最优模型与相应耦合前模型的散点图, 其中图8(a)为耦合后利用偏最小二乘算法构建的最优模型, 模型序号为43, 图8(b)为对应耦合前的散点图; 图8(c)为耦合后随机森林算法构建的最优模型, 模型序号为42, 图8(d)为对应耦合后的散点图。 从图8(a)和(b)对比分析可知, 耦合前的建模、 验证样本的样点存在成团分布的现象, 且有机质含量高的样点几乎横向集中分布于1∶ 1两侧, 而耦合后样点的分布则较为均匀的分布于1∶ 1线两侧, 样点距1∶ 1线的距离明显缩短。 由图8(c)和(d)对比分析可知, 耦合前验证样本的样点较为分散的分布于1∶ 1线两侧, 而耦合后则相对集中分布于1∶ 1线两侧。 综上可知, 本文提出的耦合算法更能有效提升跨区域土壤有机含量的估测精度, 降低模型的估测误差。

有效光谱信息的提取是利用遥感数据开展耕层土壤有机质含量检测技术研究的关键步骤, 离散小波算法是一种有效提升光谱对土壤有机质含量敏感性的方法。 然而当前针对离散小波算法的应用仅保持在基础应用, 未能有效开发离散小波算法的潜能^{[18, 19, 20]}。 基于此, 提出了一种基于离散小波算法土壤光谱信息耦合的有效方法, 该方法能有效耦合了5类各小波基的优势, 并大幅提升了光谱对土壤有机质含量的敏感性, 提高光谱对土壤有机质含量的估测能力。 研究表明与耦合前相比, 在1~10尺度内耦合后光谱与土壤有机质含量的R²平均提升了15.33%, 各估测模型的验证精度的均得到了提升, 其中基于偏最小二乘算法构建的估测模型的验证精度的R²提升了6.28%, RMSE平均降低了6.09%。 基于随机森林算法构建的估测模型的验证精度的R²平均提升了10.69%, RMSE平均降低了4.82%。 这表明本文提出的耦合算法有效、 可行。

当前, 针对耕层土壤有机质含量的研究多侧重于田间、 局部区域, 而针对构建多区域耕层土壤有机质含量监测的研究较少。 耕层土壤在大区域空间存在土壤质地、 理化组分等差异, 该差异易对土壤有机质含量的估测产生影响进而导致土壤有机质含量的估测精度较低。 本研究选用河北省石家庄市、 四川省成都市的耕地土样作为试验数据, 结合本文提出的光谱分离与聚合算法、 建模算法, 初步验证了异地耕地土壤有机质含量估测的可行性。

尽管提出的光谱信息挖掘算法, 提升了光谱对土壤有机质含量的敏感性, 提高了土壤有机质含量的估测精度, 但也存在一定不足, 仍需进一步开展相关研究, 具体如下:

(1)光谱信息耦合算法虽能有效提升土壤光谱对土壤有机质含量的敏感性, 但其提升幅度随分解尺度的增加而却呈现递减趋势。 如何提升较高分解尺度信息对土壤有机质含量敏感性是下一步深入研究的重要方向。

(2)光谱信息耦合算法虽能有效提升光谱对土壤有机质含量的敏感性, 但其是基于高光谱数据实现的, 耦合算法的提升效果是否受光谱分辨率的影响仍需进一步验证。