基于多约束优化原理的近红外多波长高温计真实温度反演算法

引用本文

张福才, 丁治宇, 盛子良, 孙晓刚. 基于多约束优化原理的近红外多波长高温计真实温度反演算法[J]. 光谱学与光谱分析, 2025,45(12): 3441-3446.
ZHANG Fu-cai, DING Zhi-yu, SHENG Zi-liang, SUN Xiao-gang. Real Temperature Inversion Algorithm for Near-Infrared Multi-Wavelength Pyrometer Based on Multi Constraint Optimization Principle[J]. Spectroscopy and Spectral Analysis, 2025,45(12): 3441-3446.
Doi:10.3964/j.issn.1000-0593(2025)12-3441-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于多约束优化原理的近红外多波长高温计真实温度反演算法

张福才¹, 丁治宇¹, 盛子良¹, 孙晓刚^2,^*

1.陕西科技大学电气与控制工程学院, 陕西西安 710021

2.哈尔滨工业大学, 黑龙江哈尔滨 150001

*通讯作者 e-mail: sxg@hit.edu.cn

作者简介: 张福才, 1978年生, 陕西科技大学电气与控制工程学院博士 e-mail: qingtengzfc@yeah.net

收稿日期: 2025-02-28 修回日期: 2025-07-19

基金: 国家重大科学仪器设备开发专项(2013YQ470767), 陕西科技大学博士科研启动基金项目(2019BJ-48)资助

摘要

多波长高温计是对被测目标在不同波长下的辐射能量同时进行测量, 通过数据处理反演真实温度。多波长高温计是非接触温度测量中重要的测量工具之一, 这种测量方法与被测目标没有物理接触, 不会对被测目标的温度和温度分布关系造成影响, 在高温和甚高温领域中有着广泛的应用。在反演真实温度过程中, 通常需要找出发射率与波长或者亮度温度等因素间的关联并以此反演被测目标的真实温度。发射率是辐射体的辐射能力的表征, 其数值大小代表了辐射体的辐射能力的强弱。在多波长辐射温度测量中, 只要能够测量出某一波长下的发射率和亮度温度, 就可以计算出辐射体的真实温度。因此, 发射率是多波长辐射温度测量中一个非常重要的物理量, 它搭建了辐射体的辐射与黑体辐射之间的桥梁, 相应的黑体辐射规律就可以应用在一般辐射体上。历经数十年持续的研究和探究, 许多国际国内专家已经取得显著进展。但发射率会随时间而变化, 若使用的发射率模型与实际情况有偏差, 那么计算出的真实温度可能会出现较大误差。再者, 要建立发射率与波长或热度等因素间的关系, 需要大量试验和实践经验的支持, 这样的数学模型并不具备广泛适用性, 特别是在检测对象发生变化的时候, 这个数学模型就变得不再有效。提出一种与发射率模型无关、具有一定通用性的多波长高温计真实温度快速反演新方法, 该方法在真实温度反演中无需考虑传统的发射率模型, 通过分析多波长高温计测量理论中内在的约束条件并与多约束优化理论相融合, 建立多波长高温计新的真实温度反演方法。通过理论推导、和实验验证了基于多约束优化理论的多波长真实温度反演方法的可行性与通用性, 初步形成一类基于多约束优化理论的多光谱高温计真实温度解决方案。

关键词: 多波长高温计; 真实温度; 发射率; 优化

中图分类号:G304 文献标志码:A

Real Temperature Inversion Algorithm for Near-Infrared Multi-Wavelength Pyrometer Based on Multi Constraint Optimization Principle

ZHANG Fu-cai¹, DING Zhi-yu¹, SHENG Zi-liang¹, SUN Xiao-gang^2,^*

1. School of Electrical and Control Engineering, Shaanxi University of Science and Technology, Xi'an 710021, China

2. Harbin Institute of Technology, Harbin 150001, China

*Corresponding author

Abstract

The Multi-wavelength pyrometer is a crucial non-contact temperature measurement instruments that simultaneously detect radiant energy from targets at different wavelengths, enabling real temperature retrieval through data processing. This measurement methodology eliminates physical contact with the measured target, thereby preserving its original thermal characteristics and temperature distribution, making it particularly valuable in high-temperature and ultra-high-temperature applications. The temperature inversion process fundamentally relies on establishing correlations between emissivity and wavelength or radiance temperature. Emissivity, a critical parameter quantifying a radiator's emission capacity relative to blackbody radiation, serves as the bridge connecting real-world radiators with blackbody radiation laws. By determining the emissivity and radiance temperature at specific wavelengths, the real temperature can be computationally derived. Despite decades of international research advancements, two persistent challenges remain: (1) Time-dependent variations in emissivity can lead to significant temperature calculation errors whenever applied models differ from actual conditions; (2) Conventional emissivity-temperature-wavelength relationship models, developed typically through rigorous experimentation and empirical validation, demonstrate limited generalizability and often fail to perform effectively whenever the objects or conditions being measured are altered. The study proposes an innovative emissivity model-independent methodology for rapid real temperature inversion in multi-wavelength pyrometry. By analyzing intrinsic constraints within multi-wavelength measurement theory and integrating them with multi-constraint optimization principles, we developed a novel temperature inversion framework. The approach eliminates traditional dependence on predefined emissivity models while maintaining measurement accuracy. Through rigorous theoretical derivation and experimental validation, we demonstrated the feasibility and universality of this multi-constraint optimization-based method, establishing a new paradigm for multi-spectral pyrometric temperature solutions. This advancement provides enhanced adaptability for diverse measurement scenarios and evolving target characteristics.

Keyword: Multi-wavelength; Real Temperature; Emissivity; Optimization

文章图片

引言

发射率表示某个物面发出的实际辐射与同波长、同温度下理想黑体所发出辐射的比值, 数值越大表示该表面的发射能力越强。但对于实际辐射目标, 其发射率通常小于1, 且会随着温度和波长的变化而改变。多波长高温计中发射率模型的选择由于发射率受到被测目标的材料性质、采用的波长范围、温度变化范围等因素的制约, 仍然是多波长高温计数据处理的核心问题之一^{[1, 2]}。围绕真实温度反演, 发射率模型主要有三类模型。一是灰体模型, 是指温度反演过程中认为发射率是一个常数, 大大降低了真实温度反演的难度, 这种方法只适用于发射率在整个测量过程中基本保持不变的测量对象, 其最早见于20世纪20年代的比色高温计^[3]。二是波长模型, 波长模型具有多样性, 应用中选择哪一种波长模型, 缺乏足够的理论支撑; 其次, 波长模型的选择又要受到被测目标的材料性质、采用的波长范围、温度变化范围等因素的影响, 因此, 在波长模型的选择上存在一定的盲目性、复杂性和通用性弱等问题^{[4, 5, 6, 7, 8]}。三是温度模型, 假设发射率与连续两次测量的真实温度差之间存在某种关系, 采用迭代和完全遍历等方式, 反演出被测目标的真实温度^{[9, 10, 11, 12, 13]}。

在对不同模型的分析基础上, 本工作以真实温度反演为研究对象, 采用目标函数、等式、不等式约束条件与多波长辐射理论相结合的研究方法, 分析多波长高温计的测量特点, 研究其内在关联性, 提出一种基于优化原理的多波长高温计真实温度反演方法, 为多波长高温计真实温度的反演提供参考与借鉴。

1 基于优化原理的多波长高温计真实温度反演理论基础

根据维恩公式与亮度温度的定义^[11], 设多波长高温计的第i个测量通道在有效波长为λ _i、真实温度T时的波长辐射亮度为 $L_{λ_{i}}$ (T), 该波长辐射亮度与某一温度T_i时的黑体波长辐射亮度 $L_{λ_{i} b}$ (T_i)相等时, 有

$L_{λ_{i}} (T) = L_{λ_{i} b} (T_{i})$ (1)

其中

$L_{λ_{i}} (T) = ε_{λ_{i}} (T) \frac{c_{1}}{λ_{i}^{5}} \frac{1}{\exp (c_{2} / (λ_{i} T)) - 1}$ (2)

$L_{λ_{i} b} (T) = \frac{c_{1}}{λ_{i}^{5}} \frac{1}{\exp (c_{2} / (λ_{i} T_{i})) - 1}$ (3)

式中, T为待测目标的真实温度(K); T_i为第i通道的亮度温度(K); λ 为有效波长(μ m); $ε_{λ_{i}}$ (T)为波长发射率; i为测量通道编号, i=1, 2, …, N; c₁为第一辐射常数, c₁=3.741 8× 10^-16 W· m²; c₂为第二辐射常数, c₂=1.438 8× 10⁴ μ m· K。

根据式(1)与式(2)和亮度温度的定义, 当

$ε_{λ_{i}} (T) \frac{c_{1}}{λ_{i}^{5}} \frac{1}{\exp (c_{2} / (λ_{i} T)) - 1} = \frac{c_{1}}{λ_{i}^{5}} \frac{1}{\exp (c_{2} / (λ_{i} T_{i})) - 1}$ (4)

时且满足维恩近似条件时, 可以将式(4)简化为

$ε_{λ_{i}} (T) \frac{1}{\exp (c_{2} / (λ_{i} T))} = \frac{1}{\exp (c_{2} / (λ_{i} T_{i}))}$ (5)

进一步约简, 得

$\frac{1}{T} = \frac{1}{T_{i}} - \frac{λ_{i}}{c_{2}} \ln \frac{1}{ε_{λ_{i}} (T)}$ (6)

式(6)即为基于维恩公式的多波长高温计的亮度温度模型。多波长高温计的每一个波长测量通道都满足式(6), 对于N个波长测量通道而言可以构成N个方程, 这N个方程中含有N个未知的波长发射率变量 $ε_{λ_{i}}$ (T)和一个未知的真实温度变量T, 由此可知, 这个方程组属于欠定方程组, 其解具有不确定性。

为了使这个方程组能够求解, 将基于优化原理的多约束优化理论引入到多波长高温计真实温度反演中, 建立一种无需假设发射率模型(without assuming emissivity model, 简称WAEM法)的多波长高温计真实温度反演方法, 实现待测目标表面真实温度反演。

1.1 反演方法的理论基础

根据式(6)可以看出, 尽管发射率是一个变量, 但从辐射测量的基本原理可知, 发射率值都位于某个区间内, 真实的温度也是有界的, 因此, 可将真实温度的反演问题转换为约束条件下的最优函数的求解问题。式(7)为多约束优化函数的基本形式, 式中, f₁(X), f₂(X), …, f_p(X)为极小值多目标函数, Rⁿ为一个向量组, X为自变量, g_j(X)≤ 0为约束条件。

$\begin{array}{l} V - \min {f_{1} (X), f_{2} (X), \dots, f_{p} (X)}, X \in R^{n} \\ s.t. \{\begin{array}{l} g_{j} (X) \leq 0 j = 1, 2, \dots, m \\ p \geq 2 \\ m \geq 1 \end{array} \end{array}$ (7)

式(7)中, P为极小值多目标函数的数量, m为多约束优化函数的数量, j为多约束优化函数的自变量, s.t.是“ subject to” 的缩写, 为“ 受约束” 或“ 使得…满足…” 之意, 主要用于表示优化问题中的约束条件。

1.2 构建极小值多目标函数

每个波长通道都可通过式(6)来计算其真实温度。由于被测目标的真实温度具有唯一性, 因此采用邻近的两个通道得到的最小的真实温度差建立一组目标函数, 即

$\begin{array}{l} F_{1} = \min (T_{1} - T_{2}) \\ F_{2} = \min (T_{3} - T_{4}) \\ F_{3} = \min (T_{5} - T_{6}) \\ F_{4} = \min (T_{7} - T_{8}) \end{array}$ (8)

由于测量中随机误差的影响, 真实温度可能会出现一定偏离, 使其测量值与实际温度产生偏差。这些偏差的分布可以通过标准差进行定量分析, 并将其方差的最小化作为目标函数, 即

$F_{5}=\min \left(\displaystyle\sum_{i=1}^{N}\left(T_{i}-\bar{T}\right)^{2} /(N-1)\right)$(9)

式(9)中, T_i为第i通道的亮度温度(K); $\overset{̅}{T}$ 为各通道表示真实温度的平均值(K); N为测量通道的数量。

根据式(8)和式(9)构造了五个目标函数, 因此, 只有同时满足这五个目标函数的解, 才能将其视为被测目标的真实温度。

1.3 真实温度不等式约束条件

由波长发射率的变化范围及式(6)可知, 待测目标的真实温度最大值T_max为

$T_{\max} \leq 1 / (\frac{λ_{\max}}{c_{2}} \times \ln (1 / ε_{λ_{i}} (T)) + \frac{1}{T_{i \max}})$ (10)

式(10)中, T_max为待测目标的真实温度最大值(K); T_i_max为所有通道亮度温度最大值(K); λ _max为波长最大值(μ m); ε _i_min为发射率的最小值。

由于发射率总小于1, 因此根据式(6), 待测目标的真实温度总大于最大亮度温度, 其真实温度的最小值的范围可限定为

$T_{\min} \geq \max (T_{i})$ (11)

式(11)中, i=1, 2, …, N, 结合式(10)与式(11), 真实温度T的不等式约束条件可归纳为

$\max (T_{i}) \leq T \leq 1 / (\frac{λ_{\max}}{c_{2}} \times \ln (1 / ε_{λ_{i}} (T)) + \frac{1}{T_{i \max}})$ (12)

式(12)中, i=1, 2, …, N。

1.4 波长与发射率的内在约束性

$T_{λ_{i}}$ 、 $T_{λ_{j}}$ 和 $T_{λ_{k}}$ 是λ _i、 λ _j和λ _k波长下的亮度温度值, 对二者进行详细的理论推导。由于被测目标本身的发射率和和波长λ _i> 0, 且发射率的范围则在0和1之间, 真实温度又总大于亮度温度, 即

$\{\begin{array}{l} 0 < T_{λ_{i}} < T \\ 0 < T_{λ_{j}} < T \\ 0 < T_{λ_{k}} < T \end{array}, \{\begin{array}{l} 0 < ε_{λ_{i}} (T) < 1 \\ 0 < ε_{λ_{j}} (T) < 1 \\ 0 < ε_{λ_{k}} (T) < 1 \end{array}$ (13)

当采用三个波长以上的多光谱技术进行测量时, 总能找到三个波长作为一组, 且满足0< λ _i< λ _j< λ _k, 由式(6)转化得

$\begin{array}{l} 2 \frac{λ_{i}}{c_{2}} \ln ε_{λ_{i}} (T) - \frac{λ_{j}}{c_{2}} \ln ε_{λ_{ij}} (T) - \frac{λ_{k}}{c_{2}} \ln ε_{λ_{k}} (T) \\ = 2 (\frac{1}{T} - \frac{1}{T_{λ_{i}}}) - (\frac{1}{T} - \frac{1}{T_{λ_{j}}}) - (\frac{1}{T} - \frac{1}{T_{λ_{k}}}) \\ = \frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} \end{array}$ (14)

式(14)的结果有三种可能性, 分别为

① 若 $\frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} > 0$ 成立, 则式(14)左侧大于零, 可得 $\frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} > 1$ ;

② 若 $\frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} < 0$ 成立, 则式(14)左侧小于零, 可得 $0 < \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} < 1$ ;

③ 若 $\frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} = 0$ 成立, 则式(14)左侧等于零, 可得 $\frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} = 1$ 。

经整理后, 得

$\begin{array}{l} \{\begin{array}{l} \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} > 1 \\ 0 < \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} < 1 \\ \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} = 1 \end{array}, \\ s.t. \{\begin{array}{l} \frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} > 0 \\ \frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} < 0 \\ \frac{1}{T_{λ_{j}}} + \frac{1}{T_{λ_{k}}} - \frac{2}{T_{λ_{i}}} = 0 \end{array} \end{array}$ (15)

通过上述公式推导, 可以看出, 当亮度温度满足一定条件时, 发射率之间只存在三种可能的情形, 这样可以在反演中去掉一部分不可能存在的发射率数据, 提高反演的速度。

1.5 发射率与亮度温度的内在约束性

根据三种不同波长处的发射率 $ε_{λ_{i}}$ , $ε_{λ_{j}}$ , $ε_{λ_{k}}$ 之间的大小关系及式(6), 可得

$\begin{array}{l} ε_{λ_{i}} (T) = e^{\frac{c_{2}}{λ_{i}} (\frac{1}{T} - \frac{1}{T_{λ_{i}}})} \\ ε_{λ_{ij}} (T) = e^{\frac{c_{2}}{λ_{j}} (\frac{1}{T} - \frac{1}{T_{λ_{j}}})} \\ ε_{λ_{k}} (T) = e^{\frac{c_{2}}{λ_{k}} (\frac{1}{T} - \frac{1}{T_{λ_{k}}})} \end{array}, (1 \leq \dots \leq i < j \leq k \dots \leq N)$ (16)

进一步可得

$\frac{2 \varepsilon_{\lambda_{i}}(T)}{\varepsilon_{\lambda_{i j}}(T) \varepsilon_{\lambda_{k}}(T)}=\mathrm{e}^{c_{2}\left[\frac{2}{\lambda_{i}}\left(\frac{1}{T}-\frac{1}{T_{\lambda_{i}}}\right)-\frac{1}{\lambda_{j}}\left(\frac{1}{T}-\frac{1}{T_{\lambda_{j}}}\right)-\frac{1}{\lambda_{k}}\left(\frac{1}{T}-\frac{1}{T_{\lambda_{k}}}\right)\right]~~~~~}$(17)

式(17)右边进一步整理, 得

$\begin{array}{l} \frac{2}{λ_{i}} (\frac{1}{T} - \frac{1}{T_{λ_{i}}}) - \frac{1}{λ_{j}} (\frac{1}{T} - \frac{1}{T_{λ_{j}}}) - \frac{1}{λ_{k}} (\frac{1}{T} - \frac{1}{T_{λ_{k}}}) \\ = \frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} \end{array}$ (18)

式(18)的结果有三种可能性, 分别为

① 当 $\frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} > 1$ 时, 又 $C_{2} > 0$ , 式(18)大于0, 即 $\frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} > 0$ ;

② 当 $\frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} < 1$ 时, 又 $C_{2} > 0$ , 式(18)小于0, 即 $\frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} < 0$ ;

③ 当 $\frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} = 1$ 时, 又 $C_{2} > 0$ , 式(18)等于0, 即 $\frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} = 0$ 。

由以上三种情况下的分析, 可得到以下结论:

$\begin{array}{l} \{\begin{array}{l} \frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} > 0 \\ \frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} < 0 \\ \frac{2}{T λ_{i}} - \frac{1}{T λ_{j}} - \frac{1}{T λ_{k}} + \frac{1}{λ_{j} T_{λ_{j}}} + \frac{1}{λ_{k} T_{λ_{k}}} - \frac{2}{T_{λ_{i}} λ_{i}} = 0 \end{array}, \\ s.t. \{\begin{array}{l} \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} > 1 \\ \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} < 1 \\ \frac{ε_{λ_{i}} {(T)}^{2 λ_{i}}}{ε_{λ_{j}} {(T)}^{λ_{j}} ε_{λ_{k}} {(T)}^{λ_{k}}} = 1 \end{array} \end{array}$ (19)

通过上述公式推导, 可以看出, 当发射率满足一定条件时, 亮度温度与波长也只存在三种可能的情形, 这样也可以在反演中去掉一部分不可能存在数据, 进一步提高反演的速度。

2 真实温度的反演验证

2.1 亮度温度测量数据

为验证提出的真实温度反演方法的可行性, 采用由意大利国家计量院的Righini博士提供的五组辐射测温数据^[14], 每一组测温数据由八个亮度温度和相应的八个测量波长组成。实验室温度范围控制在18~22 ℃, 湿度需稳定, 设备与设备之间预留50 cm以上的散热空间, 亮度温度数据和测量波长数据如表1所示。

表1 被测目标的亮度温度 Table 1 Brightness temperatures of measured target

模型编号	发射率 $ε_{λ_{i}}$ (T)范围	亮度温度 (K: 0.529 μ m)	亮度温度 (K: @0.626 μ m)	亮度温度 (K: @0.653 μ m)	亮度温度 (K: @0.687 μ m)	亮度温度 (K: @0.720 μ m)	亮度温度 (K: @0.787 μ m)	亮度温度 (K: @0.851 μ m)	亮度温度 (K: @0.968 μ m)
A	0.20~0.45	1 208.9	1 197.6	1 190.3	1 183.5	1 176.2	1 164.8	1 152.9	1 130.9
A	0.20~0.45	1 663.5	1 642.3	1 628.6	1 615.8	1 602.3	1 581.2	1 559.2	1 519.3
B	0.20~0.45	1 360.6	1 352.8	1 354.0	1 354.4	1 355.1	1 351.8	1 349.5	1 342.0
B	0.20~0.45	1 665.8	1 654.1	1 655.9	1 656.5	1 657.5	1 652.6	1 649.1	1 637.9
C	0.30~0.60	1 688.9	1 664.1	1 647.4	1 620.8	1 628.2	1 633.8	1 637.7	1 633.4
C	0.30~0.60	2 174.3	2 133.3	2 106.0	2 062.7	2 074.7	2 083.8	2 090.2	2 083.1
D	0.20~0.65	1 644.0	1 639.7	1 647.9	1 655.4	1 658.8	1 638.1	1 614.1	1 578.7
D	0.20~0.65	2 070.9	2 064.0	2 077.0	2 088.9	2 094.4	2 061.5	2 023.6	1 968.3
E	0.30~0.50	1 466.9	1 443.4	1 439.6	1 442.4	1 424.9	1 421.2	1 418.6	1 410.3
E	0.30~0.50	1 730.2	1 697.7	1 692.5	1 696.4	1 672.1	1 667.1	1 663.6	1 562.1

表1 被测目标的亮度温度 Table 1 Brightness temperatures of measured target

表2为采用SMM法和WAEM法分别实现的真实温度和反演时间的结果。从中可以看出, 无论是哪种反演方式, 其准确率均未超过1%; 从反演时间来看, 二次测量法的所需时间都在10 s以上, 但使用WAEM法所需的反演时间都在1 s以内。与SMM相比, WAEM在缩短反演周期方面有显著提升, 比例高达90%, 表明该方法在提高真实温度反演速度方面效果较好。

表2 SMM法和WAEM法反演的真实温度和时间 Table 2 Real temperature and inversion time of SMM and WAEM

模型编号	发射率 $ε_{λ_{i}}$ (T)范围	真实温度 /K	SMM法反演的结果/K	SMM法反演的相对误差 /%	SMM法反演的时间/s	WAEM法反演的结果/K	WAEM法反演的相对误差/%	WAEM法反演的时间/s	反演速度提高幅度 /%
A	0.20~0.45	1 256.0	1 244.3	-0.69	15.345 4	1 264.5	0.68	0.922 6	93.99
A	0.20~0.45	1 754.0	1 748.8	-0.30	11.669 2	1 760.7	0.38	0.932 9	92.01
B	0.20~0.45	1 456.0	1 463.5	0.52	15.892 0	1 451.3	-0.32	0.925 4	94.18
B	0.20~0.45	1 811.0	1 800.7	-0.57	18.354 1	1 795.9	-0.83	0.953 3	94.81
C	0.30~0.60	1 752.0	1 735.7	-0.64	12.640 4	1 747.4	-0.26	0.946 2	92.51
C	0.30~0.60	2 280.0	2 265.2	-0.65	13.630 6	2 283.8	0.17	0.828 8	93.92
D	0.20~0.65	1 725.5	1 719.2	-0.37	11.025 9	1 720.3	-0.30	0.986 7	91.05
D	0.20~0.65	2 201.0	2 190.2	-0.49	11.306 8	2 196.3	-0.21	0.900 8	92.03
E	0.30~0.50	1 536.8	1 524.3	-0.81	13.973 6	1 529.6	-0.47	0.895 0	93.60
E	0.30~0.50	1 828.4	1 836.3	0.43	14.025 4	1 840.0	0.63	0.897 5	93.60

表2 SMM法和WAEM法反演的真实温度和时间 Table 2 Real temperature and inversion time of SMM and WAEM

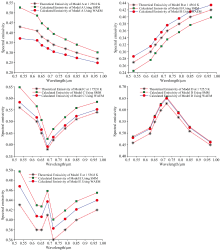
若反演得到真实温度, 利用式(6)可以计算出发射率, 如图1所示。从图中可以看出, 无论是哪种方法, 其对波长发射率随波长变动的描述都呈现出了相似的变化模式, 这也证明了这两种方法都能准确地获取到有效的发射率结果。图中为使波长发射率的细节显示的更加清晰, 将波长发射率理论值和计算值拉大了一些, 实际上三者之间差值很小。

	Figure Option View Download New Window
	图1 波长发射率随波长的变化曲线Fig.1 Variation of spectral emissivity with the wavelength

3 结论

提出了一种独立于其他发射率模型的高温计实际温度逆推策略, 其具备如下特性: 首先, 此方案并不要求对波长的发射率和波长之间关系的约束, 因此它有很强的普适性; 其次, WAEM反演速度比SMM法提高了90%; 不过, WAEM法对于发射率的变化比较敏感, 相比于二次测量法的稳定性要稍弱一些, 这也为以后的研究提供了一个方向。

参考文献

文献列表

[1]	Yang C B, Ezendeeva D, Yu T, et al. Optics Express, 2021, 29(21): 33234. [本文引用:1]
[2]	Gao S, Zhao C, Chen L, et al. Measurement Science and Technology, 2021, 32(5): 055003. [本文引用:1]
[3]	Dieter K, Koschnick K, Lill J, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2022, 277: 107978. [本文引用:1]
[4]	Guiberti T F, Krishna Y, Boyette W R, et al. Proceedings of the Combustion Institute, 2021, 38(1): 1647. [本文引用:1]
[5]	Yu K, Guo H, Zhang K, et al. Applied Optics, 2021, 60(7): 1916. [本文引用:1]
[6]	Trabold J, Butz D, Schneider S, et al. Combustion and Flame, 2022, 243: 111864. [本文引用:1]
[7]	ZHAO Yu-qing, LI Jian-qiang, SHENG Peng, et al(赵玉清, 李建强, 盛鹏, 等). Journal of Ordnance Equipment Engineering(兵器装备工程学报), 2021, 42(11): 146. [本文引用:1]
[8]	SUN Hong-sheng, LIANG Xin-gang, MA Wei-gang, et al(孙红胜, 梁新刚, 马维刚, 等). Infrared and Laser Engineering(红外与激光工程), 2021, 50(5): 36. [本文引用:1]
[9]	XI Jian-hui, JIANG Han, CHEN Bo, et al(席剑辉, 姜瀚, 陈博, 等). Journalof Shanghai JiaoTong University(上海交通大学学报), 2021, 55(7): 891. [本文引用:1]
[10]	ZHANG Ning-chao, YE Xin, LI Duo, et al(张宁超, 叶鑫, 李多, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(12): 3666. [本文引用:1]
[11]	DU Pei-jun, ZHANG Wei, ZHANG Peng, et al(杜培军, 张伟, 张鹏, 等). Acta Geodaetica et Cartographica Sinica(测绘学报), 2023, 52(7): 1090. [本文引用:2]

2021

0.0

... 多波长高温计中发射率模型的选择由于发射率受到被测目标的材料性质、采用的波长范围、温度变化范围等因素的制约, 仍然是多波长高温计数据处理的核心问题之一^[1,2] ...

2021

0.0

2022

0.0

... 一是灰体模型, 是指温度反演过程中认为发射率是一个常数, 大大降低了真实温度反演的难度, 这种方法只适用于发射率在整个测量过程中基本保持不变的测量对象, 其最早见于20世纪20年代的比色高温计^[3] ...

2021

0.0

... 其次, 波长模型的选择又要受到被测目标的材料性质、采用的波长范围、温度变化范围等因素的影响, 因此, 在波长模型的选择上存在一定的盲目性、复杂性和通用性弱等问题^[4,5,6,7,8] ...

2021

0.0

2022

0.0

2021

0.0

2021

0.0

2021

0.0

... 三是温度模型, 假设发射率与连续两次测量的真实温度差之间存在某种关系, 采用迭代和完全遍历等方式, 反演出被测目标的真实温度^{[9,10,11,12,13]} ...

2023

0.0

... 三是温度模型, 假设发射率与连续两次测量的真实温度差之间存在某种关系, 采用迭代和完全遍历等方式, 反演出被测目标的真实温度^{[9,10,11,12,13]} ...

2023

0.0

... 三是温度模型, 假设发射率与连续两次测量的真实温度差之间存在某种关系, 采用迭代和完全遍历等方式, 反演出被测目标的真实温度^{[9,10,11,12,13]} ...

... 1 基于优化原理的多波长高温计真实温度反演理论基础根据维恩公式与亮度温度的定义^[11], 设多波长高温计的第i个测量通道在有效波长为#cod#x003bb ...