鸡胸肉、 火鸡胸肉和猪排的蛋白质、 脂肪及水分含量存在显著差异, 这种差异会直接反映在近红外光谱的吸收峰位置和强度上, 如1 450 nm对应水分, 1 700 nm对应脂肪。 选择瘦肉(去骨去皮)是为了减少脂肪和结缔组织对光谱的干扰, 突出肌肉组织的主成分特征, 便于分类模型聚焦于关键波段。 这三种肉类是全球消费量最高的白肉和红肉代表, 其分类结果对食品溯源、 品质检测具有普适意义。

红富士(高糖)、 花牛(低酸)、 黄蕉(高酸)和加纳(中等糖酸比)的化学成分差异显著, 其近红外光谱在1 200 nm(糖类)和1 400 nm(有机酸)等波段存在可区分的特征峰。 四类苹果涵盖了常见口感类型(脆/绵、 甜/酸)。

从四家当地食品零售商购买了20块新鲜的鸡胸肉、 火鸡胸肉和猪排(每家店五块, 确保品牌和供应商多样性)。 所有样本(约100 g)切碎过程中去除骨头、 皮肤, 并尽量去除多余的脂肪, 只保留瘦肉^[11]。 所选零售商涵盖大型连锁超市、 农贸市场及社区生鲜店, 以反映实际消费场景且统一切割方式和部位(如猪排取背最长肌), 减少个体差异对结果的影响。 而四种苹果(红富士、 花牛、 黄蕉和加纳)均从同一超市购买, 每种苹果品种有50个样本作为实验材料, 本次实验一次购买了200个苹果。 苹果样本的选择必须满足以下要求: 所选品种涵盖脆甜(红富士)、 绵软(花牛)、 酸甜(黄蕉)等不同口感类型, 代表主流消费偏好。 肉类和苹果的样本量及选取方法^{[12, 13]}符合食品科学领域常见规范, 能够支持研究结论的普适性。 在进行近红外光谱采集之前, 实验人员擦拭了苹果表面的灰尘, 然后将苹果存放在温度为20~25 ℃、 相对湿度为50%~60%的环境中12 h^[12]。

共采集并使用了两个光谱数据集, 第一个数据集是来自肉类样本的中红外光谱^[13]。 肉类包含了60个独立样本的新鲜绞肉: 鸡肉、 猪肉和火鸡(每类20个), 使用衰减全反射采样的傅里叶变换红外光谱获取。 每个光谱包含了448个变量, 波数范围在1 000~1 900 cm^-1。

第二个数据集是来自苹果样本^[12], 包含了红富士、 花牛、 黄蕉和加纳四种类型, 是利用Antaris II NIR光谱仪获取200个苹果样本的近红外光谱。

具体的采集苹果近红外光谱的流程如下:

(1) 在采集相关数据近红外光谱数据前, 必须使光谱仪预热1 h, 使其达到稳定运行的状态;

(2) 每个品种50个样本, 波数范围在4 000~10 000 cm^-1的近红外波段, 每个光谱是1 557维的数据;

(3) 保证灯光的稳定及苹果测量时放置高度的恒定;

(4) 每个苹果样品在赤道附近用光谱仪进行三次扫描, 最后的数据为三次测试结果的平均值, 最终得到检测的苹果近红外光谱数据。

检测苹果样本近红外光谱数据^[12]时易受散射效应和颗粒大小差异因素影响, 发生基线漂移和幅度变化, 故采用光谱多元散射校正(MSC)对初始中红外光谱进行预处理, 经过散射校正后得到的光谱数据可以有效地消除由于散射水平不同带来的光谱差异^[14], 从而增强光谱与数据之间的相关性。

步骤一, 初始化: 将光谱数据分为训练样本和测试样本。 定义双曲余弦矩阵函数

$f(A)=\cosh (A)=\frac{~\exp (A)+\exp (-A)~~~}{2}$(1)

式(1)中, A是一个方阵, f(A)是以方阵A为自变量的矩阵函数。

步骤二, 确定双曲余弦矩阵函数的特征向量^[8]: 如果λ 是矩阵A的特征值, 则f(λ )是矩阵函数f(A)的特征值; 如果向量v是矩阵A属于特征值λ 的特征向量, 则向量v仍是矩阵函数f(A)属于特征值f(λ )的特征向量。

步骤三, 由双曲余弦函数f(A), 类间散度矩阵S_b, 类内散度矩阵S_w和特征值矩阵Λ _w构建投影矩阵W

$J(W)=\underset{W}{\arg \max } \frac{\left|W^{\mathrm{T}} \cosh \left(\Lambda_{b}\right) W\right|~~}{\left|W^{\mathrm{T}} \cosh \left(\Lambda_{\omega}\right) W\right|~~}$(2)

步骤四, 计算最优鉴别矢量, 即矩阵 W的列向量: cosh⁡coshSbw=λcosh⁡coshSww, 并根据其特征值进行排序, 选取前面最大的特征向量构成投影矩阵W。

步骤五, 通过一个非线性映射, 将非线性的散度矩阵映射到一个新的特征空间, 并在新的特征空间内提取特征。

步骤一, 初始化: 将肉类和苹果的光谱数据均分为训练样本和测试样本。 模糊权重指数m和类别数c, 其中m> 1;

步骤二, 计算训练样本x_k隶属于第i(1≤ i≤ c)类的初始模糊隶属度u_ik

$u_{i k}=\left[\displaystyle\sum_{j=1}^{c}\left(\frac{\left\|x_{k}-\bar{x}_{i}\right\|}{\left\|x_{k}-\bar{x}_{j}\right\|}\right)^{\frac{2}{m_{1}-1}}\right]^{-1}, \forall i, k$(3)

式(3)中, c为类别数; m₁为权重指数; ${{\bar{x}}_{i}}$为训练样本第i类的均值, ${{\bar{x}}_{j}}$为训练样本第j类的均值;

步骤三, 计算训练样本模糊类间离散矩阵S_fB, 模糊类内离散度矩阵S_fW

$S_{f B}=\displaystyle\sum_{i=1}^{c} \displaystyle\sum_{k=1}^{n} u_{i k}^{m}\left(\bar{x}_{i}-\bar{x}\right)\left(\bar{x}_{i}-\bar{x}\right)^{\mathrm{T}}$(4)

$S_{f W}=\displaystyle\sum_{i=1}^{c} \displaystyle\sum_{k=1}^{n} u_{i k}^{m}\left(x_{k}-\bar{x}_{i}\right)\left(x_{k}-\bar{x}_{i}\right)^{\mathrm{T}}$(5)

式(4)和式(5)中, uik表示训练样本 xk隶属于第 i1≤i≤c类的模糊隶属度; ${\bar{x}}$为训练样本的总均值, $\bar{x}=\frac{1}{n} \displaystyle\sum_{j=1}^{n} x_{j}$; ${{\bar{x}}_{i}}$为第 i类训练样本的均值; n为训练样本数。

步骤四, 计算模糊类内双曲余弦函数$H_{f W}=\frac{\exp \left(S_{f W}~\right)+\exp \left(-S_{f W}~\right)~~}{2}$, 模糊类间双曲余弦函数$H_{f W}=\frac{\exp \left(S_{f B}~\right)+\exp \left(-S_{f B}~\right)~~}{2}$。

步骤五, 计算特征分解: HfW-1HfBα=αλ, α和 λ分别为所求的特征向量和所对应的特征值。

K-最近邻法(K-nearest neighbor, KNN)是一种有监督的分类方法^[15]。 从测试样本点x开始不断扩大区域直到包含进k个训练样本点为止, 并且把测试样本点x的类别归为这最近的k个训练样本点中出现频率最多的类别。 根据前面两种双曲余弦判别分析方法提取出来的特征参数, 进行判别分类, 设置K值, 分别得出双曲余弦判别和模糊双曲余弦判别的分类准确率。

主成分分析(PCA)作为模式识别领域的经典特征提取方法, PCA通过线性变换将高维光谱数据投影至低维空间, 在保留原始数据最大方差的同时, 能有效消除光谱中的冗余特征。 但是, PCA在降维过程中也会丢失分类信息。 将肉类样本和苹果样本的光谱数据分别用PCA降维到2维, 最后用最近邻分类器进行分类, 分类准确率分别为85%和90.48%。

每类肉类样本中, 训练样本数为26, 测试样本数为14; 每类苹果样本中, 训练样本数为35, 测试样本数为15。 用MSC对苹果样本的近红外光谱数据进行预处理。 接着用HCMDA和FHCMDA分别计算肉类和苹果训练样本的特征向量, 实现肉类和苹果训练样本和测试样本的特征转换。 然后用KNN法进一步判别分类, 通过设置不同的K值、 模糊权重指数值m和初始模糊权重指数m₁值优化分类性能, 得到各自的分类准确率如表1和表2所示。 实验结果表明, FHCMDA在大多数情况下具有更高的分类准确率, 这是由于FHCMDA在特征提取过程中更好地处理了数据的模糊性和复杂性。 无论是肉类还是苹果的数据集, FHCMDA的准确率都比HCMDA的准确率要高, 对于肉类分类, 最佳的分类准确率在K=3, m=1, m₁=2时达到, 此时FHCMDA的准确率为97.62%, 而HCMDA的准确率为85.71%。 对于苹果分类, 最佳的分类准确率在K=3, m=2, m₁=2时达到, FHCMDA的准确率为91.67%, 而HCMDA的准确率为75.00%。

表1

Table 1

表1(Table 1)

表1 HCMDA和FHCMDA对肉类的分类准确率 Table 1 The identification accuracy of HCMDA and FHCMDA on meat Meat HCMDA/% FHCMDA/% K=1, m=1.2, m1=2.5 90.48 97.62 K=3, m=1, m1=2 85.71 97.62 K=5, m=1, m1=2.5 90.48 92.28 K=7, m=1, m1=2 85.71 90.48 K=9, m=1, m1=2.5 76.19 90.82

表1 HCMDA和FHCMDA对肉类的分类准确率 Table 1 The identification accuracy of HCMDA and FHCMDA on meat

表2

Table 2

表2(Table 2)

表2 HCMDA和FHCMDA对苹果的分类准确率 Table 2 The identification accuracy of HCMDA and FHCMDA on apple Apple HCMDA/% FHCMDA/% K=1, m=2, m1=2 76.67 91.67 K=3, m=2, m1=2 75.00 91.67 K=5, m=2, m1=2 83.33 91.67 K=7, m=2, m1=1.5 73.33 88.33 K=9, m=2, m1=1.5 76.53 90.31

表2 HCMDA和FHCMDA对苹果的分类准确率 Table 2 The identification accuracy of HCMDA and FHCMDA on apple

肉类样本和苹果样本的训练样本数和测试样本数和2.2节相同, 分别用HCMDA和FHCMDA对肉类样本和苹果样本进行特征提取, 然后再用朴素贝叶斯分类器进行分类。 苹果样本的分类准确率: HCMDA为25%, FHCMDA(m=2, m₁=2)为96.67%; 肉类样本的分类准确率: HCMDA为88.10%, FHCMDA为90.48%(m=1.2, m₁=2.5)。 可见, FHCMDA在2个数据集上的分类准确率均高于HCMDA。

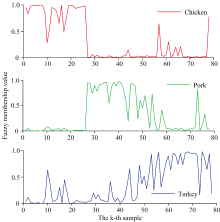
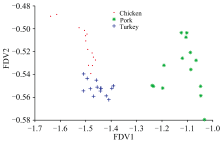
在FHCMDA算法中, 已经计算出了每个训练样本的初始模糊隶属度, 且通过实验发现FHCMDA的判别准确率较高, 所以主要利用FHCMDA和KNN对肉类和苹果进行判别分类。 模糊隶属度图展示了每个样本属于不同类别的程度, 有助于理解数据的分布情况。 图1展示了三种肉类的模糊隶属度图, 本实验有三个不同品种的肉类, 所以有三个不同的小图, 包括Chicken鸡肉, Pork猪肉, Turkey火鸡肉。 横坐标代表样本集(k-th sample代表第k个样本集), 纵坐标表示模糊隶属值。 当纵坐标值超过0.5时, 说明样本属于某类型的肉类。 在3个小图中都存在误分的样本, 比如在Chicken图中在第60和第78样本附近有大于0.5的尖峰值存在属于误分的样本。 图2展示了经过FHCMDA处理后的结果图。 其中FDV表示模糊判别向量。 从图中可以看出, FHCMDA算法能够有效地区分不同类型的肉类。 图3和图4分别展示了四种苹果的模糊隶属度图和处理后的结果图。 从图4可看出红富士和花牛存在少量样本重叠。 由经FHCMDA处理数据后的结果图可以看到, 不同类别的数据区分度比较好, 有利于后续KNN的分类。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 肉类样本的模糊隶属度图Fig.1 Fuzzy membership values of meat

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 FHCMDA处理后的肉类数据分布图Fig.2 Data distribution of meat processed by FHCMDA

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 苹果样本的模糊隶属度图Fig.3 Fuzzy membership values of apple samples

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 FHCMDA处理后的苹果数据分布图Fig.4 Data distribution of apple processed by FHCMDA