在近红外光谱实验中, 数据质量是确保模型性能可靠性的基石。 异常光谱可能源于样品污染、 仪器瞬时噪声或实验操作误差等因素, 如果参与建模的数据中掺杂波动较大的无效光谱数据, 则会干扰模型的训练过程并且降低预测精度。 为确保数据的可靠性与一致性, 本研究采用主成分分析(principal component analysis, PCA)结合马氏距离的方法进行异常光谱检测与剔除。

主成分分析通过正交变换将高维、 强相关的原始光谱数据投影到由少数几个主成分构成的低维空间, 这些主成分能够最大程度地保留原始数据的主要变异信息。 此操做可以精准有效的降低数据维度和计算过程的复杂度。

相较于忽略维度相关性的欧氏距离, 马氏距离通过解析数据的协方差结构建立统计度量框架, 能更可靠地计算样本点与数据中心(均值向量)的概率分布距离。 在PCA降维后的主成分空间中, 计算每个样本点相对于主成分得分分布中心的马氏距离。

该方法结合了PCA的降维优势和马氏距离的统计特性, 是一种高效、 鲁棒的异常光谱检测手段。 其核心优势在于能够: 有效处理高维光谱数据; 充分考虑数据的内在分布特性(协方差结构); 适用于多种光谱分析场景。

光谱数据预处理是光谱分析流程中不可或缺的关键环节, 其核心目标是消除或减弱与目标化学信息无关的物理干扰(如光散射、 基线漂移), 规范化光谱基准得以构建, 为后续建模任务的可靠实施与结果可比性奠定基础^{[12, 13]}。

标准正态变量变换(standard normal variate, SNV)的核心功能是消除近红外漫反射光谱中颗粒尺寸、 表面散射及光程变异引入的干扰。 对离群值剔除后的光谱数据实施SNV预处理。 其中SNV的数学本质是将每条光谱独立转化为均值为0、 标准差为1的标准正态分布空间, 其计算公式^[14]

$X_{i, k}=\frac{x_{i, k}-\bar{x}}{\sqrt{\frac{\displaystyle\sum_{k=1}^{m}\left(x_{i, k}-\bar{x}\right)^{2}}{m-1}}}$(1)

式(1)中, ${\bar{x}}$为第i个样品光谱平均值; k=1, 2, …, m; m为波长点数。

采用标准正态变量变换(SNV)对于NIRS数据进行预处理。 该方法基于单样本独立校正机制(不依赖全局数据集), 可以有效消除由光程差异引起的散射效应, 提升光谱数据与目标变量(酒石酸浓度)之间的相关性。 与多元散射校正(multiplicative scatter correction, MSC)相比, SNV 不依赖参考光谱, 更加简便和稳健, 因此在定量分析中被广泛使用^[15]。 该预处理流程输出的优化数据集, 为后续鲁棒建模提供了高质量数据支撑, 尤其适配在线监测中样品状态动态演化的实时需求。

用决定系数(coefficient of determination, R²)、 均方根误差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)评估模型的预测性能:

决定系数(R²): R²反映模型对数据的拟合程度^[16], 计算公式为

$R^{2}=1-\frac{\displaystyle\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\displaystyle\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}$(2)

均方根误差(RMSE): RMSE衡量预测值与参考值之间的偏差, 是评价模型预测性能常用的重要指标^[17]。 公式为

$\mathrm{RMSE}=\sqrt{\frac{1}{n} \displaystyle\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}$(3)

平均绝对误差(MAE): MAE表示预测值与实际值的平均绝对偏差, 公式为

$\text { MAE }=\frac{1}{n} \displaystyle\sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|$(4)

式(4)中, n为样本数量; y_i为第i个样本的实际值; ${\hat{y}}$为第i个样本的预测值; ${\bar{y}}$为样本实际值y_i的算数平均值。

在模型评价指标中, R²反映模型整体拟合能力, RMSE和MAE则从不同角度量化预测误差, 帮助比较模型性能。

通常, 回归方法可用于建立NIRS数据与分析物浓度之间的关系模型^[18]。 神经网络可以用于回归任务以及统计模型^[19]。 该实验中, 数据输入维度为376个特征, 对应950~1 700 nm 波长范围(2 nm分辨率)。

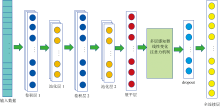
所有输入数据均通过预处理消除高频噪声、 散射效应与基线漂移。 CNN-FSA模型结构图如图1所示。 一维卷积神经网络模块采用两级串联结构:

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 CNN-FSA模型结构Fig.1 Structural configuration of the CNN-FSA model

第一级: 使用16个尺寸为20的卷积核(步长6, 填充2), 卷积结果经整流线性单元激活函数(rectified linear unit, ReLU)处理后, 接入批归一化层, 最终通过尺寸为2、 步长为2的最大池化层降维。

第二级: 配置32个尺寸为10的卷积核(步长3, 填充2), 同样经过ReLU激活、 批归一化处理, 并以相同参数(池化核尺寸2, 步长2)进行最大池化操作。

批归一化层加速了模型收敛, 池化层有效消除了原始光谱中的噪声, 从而增强了光谱特征信息, 该模块可实现光谱特征的层次化提取^[20]。 激活函数则是对卷积层的输出进行的非线性操作, 以此来提取更多的数据特征信息。 特征展平层: 将卷积模块输出的三维特征张量转换为一维特征向量, 为后续全连接层提供输入。 多层感知机模块: 单隐藏层结构; 输入维度; 输出维度。 采用带泄漏的整流线性单元(leaky rectified linear unit, LeakyReLU)激活函数(负斜率0.1)增强非线性表达能力。 通过批归一化稳定训练过程。 注意力机制受人类视觉系统启发, 模拟选择性聚焦重要区域的能力, 使模型能够对输入数据的关键特征赋予更高权重, 从而增强特征表达能力^{[21, 22]}。 特征空间注意力模块: 采用多头自注意力机制(4个注意力头), 在8维特征空间对特征进行动态加权。 该模块能自适应地增强关键化学特征的贡献, 同时抑制噪声干扰。 输出层: 包含Dropout正则化(比率0.05)防止过拟合, 以及全连接层将8维特征映射为1维浓度预测值。

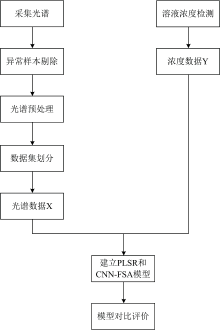
光谱分析流程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 实验光谱分析流程Fig.2 Experimental spectral analysis workflow

图2展示了该研究实验光谱分析的基本流程, 开展了六轮重复实验, 每轮包含初始底料(453.9 g水+40 g无水乙醇(乙醇浓度99.7%)+5 g无水葡萄糖+1 g苹果酸+0.1 g柠檬酸)与补料(475 g水+25 g酒石酸)的标准化物料体系。 葡萄糖(C₆H₁₂O₆)、 酒石酸(C₄H₆O₆)与乙醇(C₂H₅OH)分子均含羟基(— OH)等极性基团, 用以模拟实际多组分体系中对酒石酸定量检测的干扰。 六轮实验同步采集光谱数据及对应理化值, 构建原始数据集。 对前四轮实验数据执行异常光谱剔除之后数据按7∶ 3比例随机划分为训练集(70%)与测试集(30%)。 基于划分后的数据集, 分别采用偏最小二乘回归(PLSR)与CNN-FSA神经网络模型进行训练。 训练完成后, 两模型分别对测试集进行预测, 并计算性能指标(R², RMSE, MAE)。 对比测试集上的泛化差异和独立预测集上的鲁棒性表现。

所用试剂包括: 酒石酸(福晨(天津)化学试剂有限公司), 酒精(江苏花厅生物科技有限公司), 无水葡萄糖、 柠檬酸和苹果酸(天津聚恒达化工有限公司)。

酒石酸溶液浓度近红外在线检测系统框架如图3所示, 该装置包括反应釜、 计算机, 补料烧瓶、 电动搅拌机、 蠕动泵、 光谱仪、 流通池、 近红外光源、 短光纤。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 酒石酸溶液浓度近红外在线检测系统Fig.3 Online NIR detection system for tartaric acid concentration in solutions

采用台湾超微光学光谱仪开展实验。 该光谱仪波长范围为900~1 700 nm(实验选择实际的波段范围为950~1 700 nm), 专用于检测近红外光谱, 光谱仪分辨率设置为2 nm, 蠕动泵则是经由RS485工业总线实施闭环控制, 该设备可实现转向切换与速度的无级调节, 转速控制分辨率达± 0.1 RPM。

反应釜是双层设计, 里层盛装料液, 外层是冷却循环水, 利用制冷装置将循环冷却水降温, 保持反应釜内部液体温度在25 ℃左右。 温度检测设备使用的是BT6系列温控仪表, 分辨率0.1 C° , 测量精度± 0.5%FS。 实验时, 称取453.9 g水、 40 g无水乙醇(浓度 99.7%)、 5 g无水葡萄糖、 1 g苹果酸和 0.1 g柠檬酸, 加入烧杯中, 使用玻璃棒进行充分搅拌, 确保完全溶解, 然后倒入反应釜中。 以同样的方式称25 g酒石酸, 另取补料瓶, 加入475 g的水, 将25 g酒石酸加入补料瓶, 同时使用玻璃棒进行充分搅拌, 确保酒石酸充分溶解, 配制出质量分数为5%的酒石酸溶液。 计算机经由RS485串行总线发送指令信号, 驱动蠕动泵执行精确流量调节。 通过称量蠕动泵50次加料的总质量, 平均之后确定单次加料质量。 计算机据此即时计算并记录每次加料后反应釜中的酒石酸浓度, 并将这些数据集保存在Excel文档。

实验开始前, 反应釜里倒入料液, 打开搅拌机, 然后打开循环料液的磁吸泵保证流通池与反应釜的料液循环流通。 使用光纤将光源的出光端口与流通池的一端连接, 流通池的另一端则使用光纤连接至光谱仪, 蠕动泵上的硅胶管伸入反应釜中。 光谱波长范围选择950~1 700 nm, 2 nm分辨率共计376个波长。

为消除滴定终点蠕动泵管道内可能会掺杂空气的影响, 每轮实验数据实际结束浓度是到2.44%, 剩余数据因可能受管道内残留空气影响而舍弃。 单轮实验时长约40 min, 采样间隔约4 s, 平均每轮可获得约562条吸光度光谱(不同实验轮次略有差异)。 前四轮实验共得到2 248条数据, 剔除10%(225条)异常数据后, 保留2 023条; 后两轮实验共获得1 120条数据。

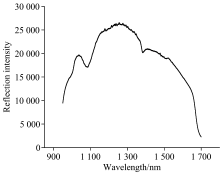
图4展示了实验过程中的背景光谱变化图, 波长范围950~1 700 nm。 背景光谱强度在950~1 100 nm保持较高水平(约25 000~30 000), 1 100 nm附近出现明显凹陷, 这一特征与光纤传输特性相关, 光纤的材料折射率或弯曲损耗在该波段引起信号衰减。 背景光谱作为参考, 用于校正样品光谱中的仪器噪声和环境干扰, 确保后续透射和吸光度计算的准确性。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 背景光谱Fig.4 Background spectrum

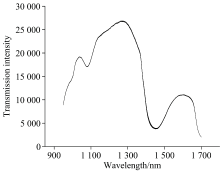
图5展示了六轮实验采集的近红外透射光谱(950~1 700 nm)叠加图。 图6展示了对应的吸光度光谱。 1 400~1 500 nm区域显示出较明显的吸收谷(对应吸光度峰)。 这些特征反映了乙醇、 葡萄糖(C— H), 水(O— H)和微量有机酸的吸收贡献。 补料(5%酒石酸)泵入40 min导致酒石酸浓度渐增至约2.5%, 但水(> 90%)的强吸收(1 450 nm)主导光谱, 不同浓度下的光谱叠加后在整个波长范围内的变化幅度相对有限。 这一现象在近红外透射光谱分析水溶液体系时较为常见, 主要归因于水分子在1 450 nm附近的强吸收主导了光谱信号, 从而导致其他成分的贡献被部分掩盖。 然而, 吸光度的细微变化模式与溶液中酒石酸浓度的增加存在关联。 背景光谱(图5)的1 100 nm凹陷在透射图中被校正, 避免仪器误差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 反应釜溶液透射光谱Fig.5 Transmission spectrum of the solution in the reactor

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 反应釜溶液吸光度Fig.6 Absorbance spectrum of the solution in the reactor

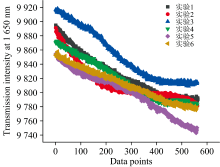
图7展示了六轮实验在1 650 nm波长点处的透射光谱强度随实验变化的趋势图。 近红外光谱技术准确性来自于此技术对样品内部物理及化学信息的感知^[23]。 近红外光的散射和吸收与介质中存在的分子的化学键的分子振动有关。 图中清晰显示, 透射强度从初始强度约9 920逐渐下降至约9 760, 变化幅度约1.6%, 表明样品对该波段的吸收增强。 透射光谱总体呈下降趋势, 局部存在轻微波动, 表明实验过程中样品对该波长近红外光的吸收持续增强。 虽然水分子在此波段也有贡献, 但1 650 nm处透射强度呈现独立的下降趋势(对应吸光度上升, 图8)。 补料泵入导致浓度增加, 透射下降趋势与酒石酸累积相关, 不同轮次间分化反映实验操作细节的影响。 乙醇和葡萄糖的干扰在此波段较弱, 强化了酒石酸检测的特异性。 结合酒石酸分子中含有的羧基和羟基基团, 可以认为酒石酸浓度的增加是导致该波段吸收增强的重要因素之一。 不同轮次间的透射强度分布存在重叠但有分化, 反映了实验操作细节(如补料添加的微小时间差异)对光谱特征的微弱影响。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 1 650 nm波长点光透射谱强度变化Fig.7 Transmission spectral intensity variation at 1 650 nm

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 1 650 nm波长点吸光度变化Fig.8 Absorbance variation at 1 650 nm in the reactor solution

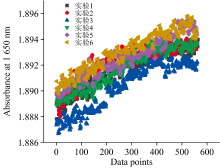
图8展示了1 650 nm处吸光度(基于图8透射强度和背景光谱计算)随实验的变化, 可以看到, 吸光度随实验进行而逐渐增加, 与酒石酸浓度增加一致。

在训练该神经网络模型时, 采用带权重衰减的自适应矩估计(adaptive moment estimation with weight decay, AdamW)作为优化器, 学习率初始值设置为0.001。 损失函数选用均方误差作为优化目标, 批量大小固定为32。 最大训练轮数设置为500轮, 同时实施双重早停机制。 学习率调度策略采用平台自适应学习率调整(reduce learning rate on plateau, ReduceLROnPlateau), 当验证损失连续200轮无改善时, 学习率衰减为原来的50%(衰减因子0.5)。

图9分别展示了利用前四轮实验吸光度数据(训练集∶ 测试集=7∶ 3)构建的偏最小二乘回归(PLSR)模型和CNN-FSA在训练集和测试集上的回归性能散点图。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 (a) PLSR模型拟合回归曲线; (b) CNN-FSA模型拟合回归曲线Fig.9 (a) Fitted regression curves of the PLSR model; (b) Fitted regression curves of the CNN-FSA model

表1的模型性能对比表明两模型的预测值与实际观测值均高度相关, 散点紧密分布在理想拟合线附近。 无论是训练集还是测试集, R²值均较高, RMSE和MAE值较低, 表明两种模型对训练数据均具有极强的拟合能力, 在内部测试集上也表现出优异的预测精度, 且两者性能接近。

表1

Table 1

表1(Table 1)

表1 两种模型在训练集和测试集上的拟合效果对比 Table 1 Comparative fitting performance of PLSR and CNN-FSA models on training/test sets 模型类型 数据集 R2 RMSE MAE PLSR 训练集 0.996 666 0.000 328 0.000 261 测试集 0.996 079 0.000 360 0.000 290 CNN-FSA 训练集 0.993 554 0.000 456 0.000 368 测试集 0.993 322 0.000 470 0.000 387

表1 两种模型在训练集和测试集上的拟合效果对比 Table 1 Comparative fitting performance of PLSR and CNN-FSA models on training/test sets

图10展示了基于两轮独立预测数据的偏最小二乘回归(PLSR)和卷积神经网络模型的预测性能。 真实值和预测值随时间呈一致上升趋势, 值域为0.000~0.025, 反映了实验过程中酒石酸浓度的动态变化。 表2列出了PLSR和CNN-FSA两种模型对独立预测数据的评价指标。 PLSR模型的决定系数(R²)为0.968 750, 均方根误差(RMSE)为0.001 214, 平均绝对误差(MAE)为0.001 059; CNN-FSA模型的R²为0.989 558, RMSE为0.000 702, MAE为0.000 580。 相比之下, CNN-FSA模型通过卷积结构和注意力机制有效捕捉光谱中的非线性特征, 预测精度显著优于PLSR模型(RMSE降低42.17%, MAE降低45.23%)。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 (a) PLSR模型预测结果; (b)CNN-FSA模型预测结果Fig.10 (a) Predicted results of the PLSR model; (b) Predicted results of the CNN-FSA model

表2

Table 2

表2(Table 2)

表2 PLSR和CNN-FSA两种模型在预测样本上的预测效果对比 Table 2 Comparative prediction performance of PLSR and CNN-FSA models on the prediction set 模型类型 R2 RMSE MAE PLSR 0.968 750 0.001 214 0.001 059 CNN-FSA 0.989 558 0.000 702 0.000 580

表2 PLSR和CNN-FSA两种模型在预测样本上的预测效果对比 Table 2 Comparative prediction performance of PLSR and CNN-FSA models on the prediction set

图11展示了PLSR和CNN-FSA模型在独立预测数据集各样本的绝对误差及其平均绝对误差(MAE)。 结果表明, CNN-FSA模型的MAE为0.000 580, 最大误差为0.002 363; PLSR模型的MAE为0.001 059, 最大误差为0.003 594。 CNN-FSA模型的误差波动总体小于PLSR模型, 表明CNN-FSA在独立预测数据上的精度上优于传统的PLSR。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 (a) PLSR模型预测样本绝对误差; (b) CNN-FSA模型预测样本绝对误差Fig.11 (a) Absolute prediction errors of the PLSR model samples; (b) Absolute prediction errors of the CNN-FSA model samples